不同水灰比的牛顿型水泥浆液流变性随时间变化规律

杨志全，丁 一，杨 溢，朱颖彦,2，张 杰，郭永发，陈兴贵

不同水灰比的牛顿型水泥浆液流变性随时间变化规律

杨志全1，丁 一1，杨 溢1※，朱颖彦1,2，张 杰3，郭永发4，陈兴贵5

（1. 昆明理工大学公共安全与应急管理学院，昆明 650093； 2.中国科学院水利部成都山地灾害与环境研究所，成都 610041；3. 云南省地质环境监测院，昆明 650216； 4. 中铁二院昆明勘察设计研究院有限责任公司，昆明 650200；5. 中铁七局集团第三工程有限公司，西安 710026）

水化时间与水灰比对水泥浆液流变性有重要影响，进而决定浆液在岩土体中的运动扩散效果。为研究水化时间与水灰比综合作用对牛顿型水泥浆液流变性的影响作用，以目前实践工程中广泛应用的普通硅酸盐水泥浆液为研究对象，采用NXS–11A 型旋转黏度计对水灰比为1.5、2.0、5.0、10.0的水泥浆液分别在0、5、10、20、30及60 min 6个水化时间的流变性进行了试验研究，并探讨了水化时间、水灰比及其综合作用对牛顿型水泥浆液流变性的定量变化规律。研究结果表明：水化时间、水灰比均对牛顿型水泥浆液动力黏度具有显著性的影响，牛顿型水泥浆液动力黏度随水化时间表现为增长的变化趋势，而随水灰比则呈现为下降的变化规律；指数模型是反映水化时间与水灰比综合作用对牛顿型水泥浆液动力黏度定量变化关系的较优模型，由其得到的理论值与试验值间的误差均在 10%以内，而由线性、对数与幂函数3种模型得到的理论值与试验值间有80%的误差都大于 10%；并以此构建了考虑水化时间与水灰比综合作用的牛顿型水泥浆液流变方程。研究结果对水泥浆液流变性理论的发展和完善具有一定的理论意义，也可为建筑物基础托换、隧道堵水防渗、基坑加固、地质灾害防控、农业水土保持等实际工程应用提供一定的技术支撑。

试验；水化时间；水灰比；水泥浆液；流变性

0 引 言

水泥作为一种成本低廉与性能良好的无机胶凝材料，在当前的农业、公路、铁路、矿山、隧道、高铁、边坡、建筑、水电等领域的灌浆、注浆、堵水防渗及岩土加固等实践工程中得到了极其广泛地应用。水泥浆液的流变性不仅决定着其在岩土体中的迁移扩散范围大小，而且对实际的工程效果也具有非常重要的影响。因此，开展水泥浆液流变性的研究既可为开展其迁移扩散运动研究提供理论基础，也可为实践工程设计提供技术支撑[1-3]。

水泥浆液流变性主要受水化时间、组成成分、水灰比、环境温度等因素的影响。目前，国内外学者在这些领域开展了较为深入的探索，并取得了一定的研究成果。在水化时间对水泥浆液流变性影响方面，刘泉声等[4]分析了水化时间对水泥浆液流变性的影响；阮文军[5]研究了浆液黏度随时间的定量变化规律；袁敬强等[6-7]分别探索了静、动水条件下浆液黏度时变特性；Roussel等[8]提出了浆液在瞬态状态下的流变性变化模型；Yang等[9]探讨了时变性水泥浆液在实践岩土体工程中的应用。考虑组成成分对浆液流变性影响方面，Mirza等[10-11]研究了粉煤灰-水泥浆液在不同配比下的流变性能；Mahaut等[12]考虑了粗细颗粒体积分数对浆液流变性的影响；Chen等[13]分析了浓缩硅粉对浆液流变性的变化规律；杨晓华等[14]开展了添加剂对水泥浆液流变性影响的研究；Li等[15]探讨了超细水泥的流变性；王星华等[16-17]研究了黏土-水泥浆与SJP浆液的流变性能；Vasumithran等[18-19]分析了聚合物对水泥浆液流变性的改变作用。在水灰比对水泥浆液流变性影响方面，Mirza等[20-21]研究了水灰比对浆液流变性的改变规律；Yang等[22-23]讨论了水灰比对水泥浆液流型的影响；Zou等[24]分析了幂律型水泥浆液的流变性；曹明莉等[25]探索了不同水灰比与砂灰比条件下碳酸钙晶对水泥砂浆流变性的变化规律。对于温度对其流变性影响领域，刘泉声等[4,26-27]分析了温度对水泥浆液流变性的影响规律；Petit等[28]研究了温度对流动砂浆流变性的变化特征。通过分析总结以上相关的国内外文献可知：目前的研究成果仅从单因素对水泥浆液流变性影响的角度开展研究，而这些因素的综合作用对其影响效应还未较好地把握。

当前，牛顿型水泥浆液在国内外众多的注浆工程实践中具有较广泛的应用。依据不同的流变本构方程，水泥浆液可分为牛顿、宾汉姆与幂律流体3种类型[1]；其中，牛顿流体是单相均匀体系，属于黏性流体，其流变曲线是通过原点的直线，水、多数化学浆液及水灰比较大的水泥浆液为牛顿流体。如，目前工程常用的水泥浆液在水灰比大于1.25的条件下属于典型的牛顿流体[23]。基于此，本文分析不同水灰比的牛顿型水泥浆液流变性随水化时间的变化规律，探索水化时间与水灰比综合作用对牛顿型水泥浆液动力黏度的定量变化关系模型，并以此为基础构建考虑水化时间与水灰比综合作用的牛顿型水泥浆液流变方程，拟为建筑物基础托换、隧道堵水防渗、基坑加固、地质灾害防控、农业水土保持等实际工程应用提供一定的理论支撑。

1 材料与方法

1.1 试验材料及设备

试验材料选用昆明水泥厂生产的#32.5普通硅酸盐水泥，该标号水泥在目前的实践工程中被广泛使用。

流变试验采用成都仪器厂生产的NXS–11A 型旋转黏度计（图1）。不同水灰比的牛顿型水泥浆液试样采用电子天平（由佛山市中准衡器有限公司生产的JJ1000g型，精度0.01 g）、量筒与烧杯制备得到。试验用水采用饮用纯净水。

图1 NXS-11A型旋转黏度计

1.2 试验设计及方法

依据目前水泥浆液在水灰比大于1.25时属于牛顿流体的研究成果[23]及GB175-2007国家标准中关于通用硅酸盐水泥初凝时间不得早于45 min的规定[29]，本研究拟设计开展水灰比1.5、2.0、5.0、10.0水泥浆液分别在0、5、10、20、30与60 min水化时间的流变试验。同时，设计的流变试验温度为常温（25 ℃），因此要求开展的所有流变试验的室内环境温度与制备水泥浆液试样的水温均保持在（25±2）℃的条件。

水泥浆液试样制备方法：每次首先用电子天平称量300 g饮用纯净水并倒入量筒，然后采用电子天平称量200 g#32.5普通硅酸盐水泥并放入烧杯，然后将量筒中的水完全倒入烧杯并搅拌即可制备得到水灰比1.5的水泥浆液；照此方法，采用电子天平分别称量150、60、30 g #32.5普通硅酸盐水泥，并加入300 g饮用纯净水搅拌，同理可制备得到水灰比为2.0、5.0与10.0的水泥浆液。

流变试验方法：将制备得到的不同水灰比水泥浆液加入NXS—11A型旋转黏度计外筒，将内筒的测量头垂直地插入外筒并固定；接通电源，打开剪切速度旋钮与控制开关即开展流变试验；通过调节剪切速度旋钮可开展不同剪切速度的流变试验，并同时测定得到对应的剪切应力；然后在剪切速度—剪切应力坐标中可绘制得到不同水灰比的牛顿型水泥浆液流变曲线。

为保证试验结果的可靠性与准确性，对同一水泥浆液试样在相同的试验条件下，至少测量3次，保证其标准差在5%的范围内，然后取平均值进行分析。

2 结果与分析

2.1 牛顿型水泥浆液流变曲线与流变方程

依据流变试验结果可得到4种水灰比水泥浆液的流变曲线，如图2所示。4种水灰比水泥浆液在6个水化时间流变曲线的变化趋势均符合牛顿流体基本流变曲线[30-31]，证明了牛顿型水泥浆液的流变类型不随水化时间发生改变，与文献[5]的研究成果一致。

以式（1）所示的牛顿流体基本流变方程为理论基础[30-31]，依据图2所示的流变曲线可得到这4种水灰比牛顿型水泥浆液在6个水化时间的流变方程，如表1。

式中为剪切应力，Pa；为动力黏度，Pa·s；为剪切速率，s-1；通常采用动力黏度来表征牛顿流体流变性。

分析表1可知：水化时间与水灰比均对牛顿型水泥浆液动力黏度具有较大的影响。水化时间与牛顿型水泥浆液动力黏度表现为增长的变化趋势；这是由于硅酸盐水泥遇水后，随着水化时间增长，水泥浆液中的物性成分发生改变，从而引起其动力黏度的增长。然而，水灰比与牛顿型水泥浆液动力黏度则呈现为下降的变化规律；这是因为水灰比越大，浆液中含有纯净水比例越高，水泥浆液流动性越好，由此导致其动力黏度越低。

2.2 水化时间与水灰比综合作用对牛顿型水泥浆液流变性的定量变化规律

2.2.1 双因素方差分析

采用Origin 2018进行水化时间与水灰比综合作用对牛顿型水泥浆液动力黏度影响的双因素方差分析，结果如表2。

分析表2可知：水化时间与水灰比均对牛顿型水泥浆液动力黏度均具有显著的影响，这也从统计学角度证实了在2.1中得到的水化时间与水灰比均对牛顿型水泥浆液动力黏度具有较大影响的试验结论。

图2 4种水灰比ω牛顿型水泥浆液在不同水化时间下的液流变曲线

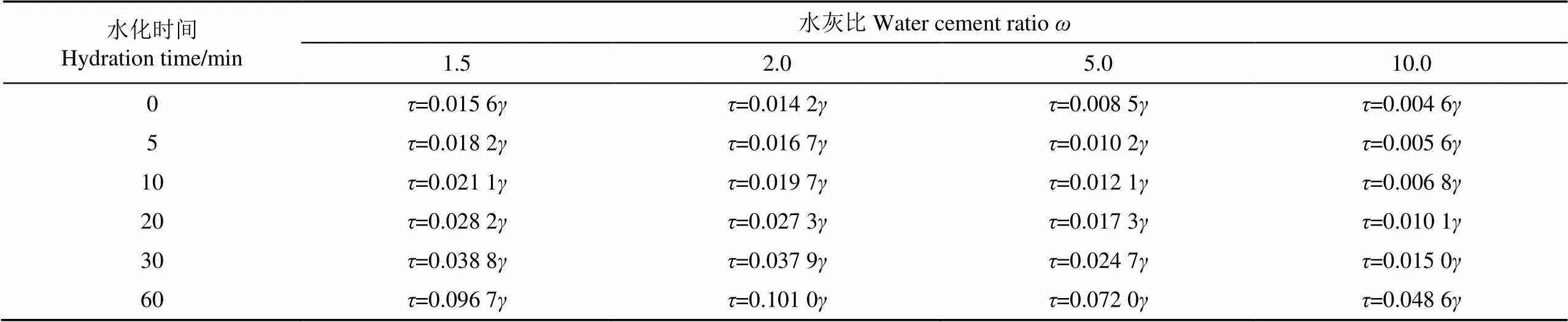
表1 4种水灰比牛顿型水泥浆液在6个水化时间的流变方程

注：为剪切应力，Pa；为剪切速率，s-1.

Note:is shear stress, Pa;is shear rate, s-1.

表2 水化时间与水灰比综合作用对牛顿型水泥浆液动力黏度影响的双因素方差分析

注：<0.05且>0.05表示具有显著影响。

Note:<0.05 and>0.05mean that it has significant effect.

2.2.2 定量变化关系

1）构建定量变化关系模型

选用数学上最基础且实践中应用最广泛的4种函数关系构建模型：线性模型、对数模型、指数模型及幂函数模型，并以此为基础采用数值分析方法及Origin 2008软件探讨水化时间与水灰比综合作用对牛顿型水泥浆液动力黏度的定量变化关系；再依据统计学理论与验证试验两方面的综合分析结果确定其较优模型。

拟合得到的水化时间-水灰比综合作用与牛顿型水泥浆液动力黏度间的线性、指数、幂函数与对数函数4种变化关系模型及对应的分析结果见表3。

表3 水化时间-水灰比综合作用与牛顿型水泥浆液动力黏度间变化关系的4种拟合模型及对应的分析结果

注：为动力黏度， Pa·s；为水化时间， min；为水灰比。

Note:is dynamic viscosity, Pa·s;is hydration time, min;is water cement ratio.

由表3可知：指数模型的2与2(adj)最大，均超过了0.95，表明指数模型是4种拟合模型中拟合优度最好的；4种拟合模型及水化时间与水灰比对应的值均大于临界值0.05；同时它们的值都小于0.05；则表明4种拟合模型均通过了拟合模型及其回归系数的显著性检验。

综合分析上述检验结果可得：指数模型是4种模型中反映水化时间与水灰比综合作用对牛顿型水泥浆液动力黏度的定量变化关系的较优模型。

2）验证定量变化关系模型

拟合模型的选取除考虑统计学理论外，还应检验其在实践中的适用性与精确性。设计水灰比为1.75的水泥浆液在0、3、12、21、40及50 min、水灰比为3.5的水泥浆液在0、6、15、24、35及45 min与及水灰比7.5的水泥浆液在0、9、18、27、45及55 min的3组试验（编号分别为G1、G2、G3）对表3中构建的定量关系模型进行验证。3组试验采用的材料、试验设备及试验条件同前文。

水化时间-水灰比综合作用与牛顿型水泥浆液动力黏度间试验组G1、G2、G3的4种定量变化关系模型验证结果如表4所示。

表4 水化时间-水灰比综合作用与牛顿型水泥浆液动力黏度间的4种定量变化关系模型验证结果

分析表4可得：指数模型较其他3种模型（线性、对数与幂函数模型）计算得到的理论值与试验值更一致。其理论值与试验值间的误差均在 10%以内，同时差异间的变化幅度较小，最大变化幅度仅3%；而其他的理论值与试验值间 80%的误差都大于 10%，且误差间的变化幅度均超过了 35%，甚至最大变化幅度达到了 134%。由此可见，从实践适用性与精确性的角度，指数模型是 4 种模型中反映水化时间与水灰比综合作用对牛顿型水泥浆液动力黏度的定量变化关系的较优模型。

综上所述，反映水化时间与水灰比综合作用对牛顿型水泥浆液动力黏度的定量变化关系的较优模型为指数模型，即

联立式（1）、（2）可得到考虑水化时间与水灰比综合作用的牛顿型水泥浆液流变方程

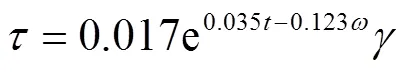
由式（3）可快速得到具体水灰比的牛顿型水泥浆液在不同水化时间条件下的流变性，进而可为实际工程应用提供一定的理论支撑。

3 结 论

以目前实践工程中广泛应用的普通硅酸盐水泥浆液为研究对象，对常温（25±2）℃条件下水化时间与水灰比综合作用对牛顿型水泥浆液流变性的定量变化规律开展研究，得到以下结论：

1）水化时间与水灰比对牛顿型水泥浆液动力黏度均具有显著影响：牛顿型水泥浆液动力黏度随水化时间表现为增长的变化趋势，而随水灰比则呈现为下降的变化规律。

2）从统计学理论、实践适用性及精确性角度分析得到指数模型是反映水化时间与水灰比综合作用对牛顿型水泥浆液动力黏度定量变化关系的较优模型，由指数模型得到的理论值与试验值间的误差均在 10%以内，而由线性、对数与幂函数3种模型得到的理论值与试验值间有80%的误差都大于10%；并由反映它们定量变化关系的指数模型构建了考虑水化时间与水灰比综合作用的牛顿型水泥浆液流变方程，可快速得到具体水灰比的牛顿型水泥浆液在不同水化时间条件下的流变性。

本文的研究成果不仅对水泥浆液流变性理论的发展和完善具有一定的理论意义；而且也可为建筑物基础托换、隧道堵水防渗、基坑加固、地质灾害防控、农业水土保持等实际工程应用提供一定的技术支撑。

[1] 王国际. 注浆技术理论与实践[M]. 徐州：中国矿业大学出版社，2000.

[2] Axelsson M, Gustafson G. A robust method to determine the shear strength of cement-based injection grouts in the field[J]. Tunnelling and Underground Space Technology, 2006, 36(5): 499-503.

[3] 杨溢，卢杰，杨志全，等.花管注浆加固松散碎石土层试验与效果参数预测模型[J]. 农业工程学报，2018，34(24)：151-157.

Yang Yi, Lu Jie, Yang Zhiquan, et al. Experiments and effect parameters prediction model of reinforcement loose gravel soil-layers by flower pipe grouting[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(24): 151-157. (in Chinese with English abstract)

[4] 刘泉声，卢超波，刘滨，等. 考虑温度及水化时间效应的水泥浆液流变特性研究[J]. 岩石力学与工程学报，2014，33(S2)：3730-3740.

Liu Quansheng, Lu Chaobo, Liu Bing, et al. Study on rheological properties of cement slurry considering the effects of temperature and hydration time[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(S2): 3730-3740. (in Chinese with English abstract)

[5] 阮文军. 注浆扩散与浆液若干基本性能研究[J]. 岩土工程学报，2005，27(1)：69-73.

Ruan Wenjun. Research on diffusion of grouting and basic properties of grouts[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 69-73. (in Chinese with English abstract)

[6] 袁敬强，陈卫忠，于建新，等. 静水条件下浆液黏度时变特性与微观结构研究[J]. 地下空间与工程学报，2016，12(5)：1264-1270.

Yuan Jingqiang, Chen Weizhong, Yu Jianxin,et al. Study on time-varying characteristics and microstructure of slurry viscosity under still water condition[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(5): 1264-1270. (in Chinese with English abstract)

[7] 李术才，韩伟伟，张庆松，等. 地下工程动水注浆速凝浆液黏度时变特性研究[J]. 岩石力学与工程学报，2013，32(1)：1-7.

Li Sucai, Han Weiwei, Zhang Qinsong, et al. Study on time-varying viscosity of dynamic water grouting slurry in underground engineering[J]. Chinese Journal of Geotechnical Engineering, 2013, 32(1): 1-7. (in Chinese with English abstract)

[8] Roussel N, Roy R L, Coussot P. Thixotropy modelling at local and macroscopic scales[J]. Non-Newtonian Fluid Mech, 2004, 117(2): 85-95.

[9] Yang Z Q, Qian S G, Hou K P. Time-dependent Behavior Characteristics of Power-law Cement Grouts Applied in geotechnical Engineering[J]. ElectronicJournal of Geotechnical Engineering, 2015, 20(22): 1017-1023.

[10] Mirza J, Mirza M S, Roy V, et al. Basic rheological and mechanical properties of high-volume fly ash grouts[J]. Constr Build Mater, 2002, 16(6): 353-363.

[11] Zhang S, Qiao W G, Chen P C, et al. Rheological and mechanical properties of microfine-cement-based grouts mixed with microfine fly ash, colloidal nanosilica and superplasticizer[J]. Construction and Building Materials, 2019, 212: 10-18.

[12] Mahaut F, Mokéddem S, Chateau X, et al. Effect of coarse particle volume fraction on the yield stress and thixotropy of cementitious materials[J]. Cement and Concrete Research, 2008, 38(11): 1276-1285.

[13] Chen J J, Fung W W, Kwan A K H. Effects of CSF on strength, rheology and cohesiveness of cement paste[J]. Construction and Building Materials, 2012, 35: 979-987.

[14] 杨晓华，郑坤隆，徐礼笑. 渗透结晶型材料添加剂对水泥浆液性能影响试验[J]. 中国公路学报，2019，32(7)：129-135.

Yang Xiaohua, Zheng Kunlong, Xu Lixiao. Experiment on effect of capillary crystalline material additives on cement slurry performance[J]. China Journal of Highway and Transport, 2019, 32(7): 129-135. (in Chinese with English abstract)

[15] Li W, Shaikh F UA, Wang L, et al. Experimental study on shear property and rheological characteristic of superfine cement grouts with nano-SiO2addition[J]. Construction and Building Materials, 2019, 228: 146-153.

[16] 王星华. 粘土-水泥浆流变性及其影响因素研究[J]. 岩土工程学报，1997，19(5)：45-50.

Wang Xinghua. Study on rheological properties of clay-cement slurry and its influencing factors[J].Chinese Journal of Geotechnical Engineering, 1997, 19(5): 45-50. (in Chinese with English abstract)

[17] 裴向军，张佳兴，王文臣，等. SJP注浆浆液水化进程与流变特性研究[J]. 岩土工程学报，2017，39(2)：201-209.

Pei Xiangjun, Zhang Jiaxing, Wang Wencheng, et al. Study on hydration process and rheological characteristics of SJP grouting grout[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(2): 201-209. (in Chinese with English abstract)

[18] Vasumithran M, Anand K B, Sathyan D. Effects of fillers on the properties of cement grouts[J]. Construction and Building Materials, 2020, 246: 1146-1154.

[19] Mohammed A, Mahmood W, Ghafor K, et al. Rheological properties with maximum shear stress and compressive strength of cement-based grout modified with polycarboxylate polymers[J]. Construction and Building Materials, 2020, 235: 1175-1183.

[20] Mirza J, Saleh K, Langevin M A, et al. Properties of microfine cement grouts at 4 degrees C, 10 degrees C and 20 degrees C[J]. Construction and Building Materials, 2013, 47: 1145-1153.

[21] 王丽娟，周建华，李凯. 对不同水灰比的静置浆液黏度测量的研究[C]//第14次全国水利水电地基与基础工程学术研讨会论文集. 北京：中国水利水电出版社，2017：559-565.

Wang Lijuan, Zhou Jianhua, Li Kai.Research on viscosity measurement of static slurry with different water cement ratio[C]//Proceedings of the 14th National Symposium on foundation and foundation engineering of water conservancy and hydropower.Beijing: China Water Conservancy and Hydropower Press, 2017: 559-565. (in Chinese with English abstract)

[22] Yang Z Q, Niu X D, Hou K P, et al. Relationships between water-cement ratio and rheological characteristics of Power-law cement grouts[J]. Electronic Journal of Geotechnical Engineering, 2015, 34(7): 1415-1425.

[23] Yang Z Q, Hou K P, Guo T T. Study on the effects of different water-cement ratios on the flow pattern properties of cement grouts[J]. Applied Mechanics and Materials, 2011, 149: 1264-1267.

[24] Zou L, Håkansson U, Cvetkovic V. Yield-power-law fluid propagation in water-saturated fracture networks with application to rock grouting[J]. Tunnelling and Underground Space Technology, 2020, 95: 1031-1038.

[25] 曹明莉，许玲，张聪. 不同水灰比、砂灰比下碳酸钙晶对水泥砂浆流变性的影响[J]. 硅酸盐学报，2016，44(2)：246-252.

Cao Mingli, Xu Lin, Zhang Cong. Effect of calcium carbonate whisker on rheological property of cement mortar under different water - cement ratio and sand - cement ratio[J]. Bulletin of the Chinese Ceramic Society, 2016, 44(2): 246-252. (in Chinese with English abstract)

[26] Liu Q, Lei G, Peng X, et al. Rheological Characteristics of cement grout and its effect on mechanical properties of a rock fracture[J]. Rock Mechanics and Rock Engineering 2018, 51(2): 613-625.

[27] Bohloli B, Skjolsvold O, Justnes H, et al. Cements for tunnel grouting-Rheology and flow properties tested at different temperatures[J]. Tunnelling and Underground Space Technology, 2019, 9: 1030-1041.

[28] Petit J Y, Wirquin E, Khayat K H. Effect of temperature on the rheology of flowable mortars[J]. Cement & Concrete Composites, 2009, 32(1): 43-53.

[29] 中国国家标准化管理委员会. GB175-2007通用硅酸盐水泥[S]. 北京：中国标准出版社，2007.

[30] 沈崇棠，刘鹤年.非牛顿流体力学及其应用[M]. 北京：高等教育出版社，1989.

[31] 孔祥言. 高等渗流力学[M]. 北京：中国科学技术大学出版社，1999.

Hydration-time-dependent rheological behaviors of Newtonian cement grouts with different water cement ratios

Yang Zhiquan1, Ding Yi1, Yang Yi1※, Zhu Yingyan1,2, Zhang Jie3, Guo Yongfa4, Chen Xinggui5

(1.,,650093,; 2.,,610041,; 3.,650216,; 4.,,,650200,; 5.,,710026,)

As an inorganic cementitious material with low cost and good property, cement grouts has been widely used in many engineering fields such as highways, tunnel, slopes, foundations, railways, construction, mining and water conservancy. As for cement grouts, the rheological properties of cement grouts are significantly affected by the changes of the hydration time and the water cement ratio, which determine the diffusion state of cement grouts in rocks and soils and have a great influence on the outcome of projects. However, the current research only considered the influence of a single factor on rheological properties of cement grouts, the combined effect of these factors has not been well understood. In this study, Portland cement grouts, a widely used material in practical grouting engineering are used as the research object and the Portland cement grouts with four water cement ratios which are the typical cement ratio of Newtonian fluid (1.5, 2.0, 5.0,10.0) at six moments (0,5,10, 20, 30 and 60 min) were chosen as the experimental group, then combined with the numerical analysis and the theoretical method the effect of hydration time and water cement ratio on rheological properties of Newtonian cement grouts was studied. The results show that: the hydration time and the water cement ratio both have significant influence on dynamic viscosity of Newtonian cement. The former shows a trend of growth, and the longer the hydration time is, the faster the growth trend, the latter shows a trend of decreased, and the smaller the water cement ratio is, the more significant the decreasing trend. Combined with the perspective of statistical theory, practical applicability and accuracy, this study selects four theoretical models to discuss the quantitative relationship of the effect of hydration time and water cement ratio on rheological properties of Newtonian cement grouts, and the four theoretical models are the most basic in mathematics, also the most widely used in practice: the linear model, exponential model, power function model and logarithm model. Then the optimal model will be determined from the fourth according to statistical theory and experimental verification. Comparing the determination coefficients and the regression values of the four fitting models, the exponential model is the optimal model for the quantitative change of dynamic viscosity of Newtonian cement to react the effect of hydration time and water cement ratio on rheological properties of Newtonian cement grouts. The difference between the theoretical value and the experimental value of the exponential model is within 10%, while more than 80% of the difference between the theoretical value and the experimental value of linear, logarithmic and power function models are greater than 10%. Thus, the rheological equation of Newtonian cement considering the hydration time and the water cement ratio are built. The research results can not only improve the rheological theory of Newtonian cement grouts, but also provide certain technical support for practical engineering applications such as the building foundation support, tunnel water plugging and seepage prevention, foundation reinforcement, geological disaster prevention and control, and agricultural soil conservation.

experiments; hydration time; water cement ratio; cement grouts; rheological properties

杨志全，丁一，杨溢，等. 不同水灰比的牛顿型水泥浆液流变性随时间变化规律[J]. 农业工程学报，2020，36(19)：161-167.doi：10.11975/j.issn.1002-6819.2020.19.018 http://www.tcsae.org

Yang Zhiquan, Ding Yi, Yang Yi, et al. Hydration-time-dependent rheological behaviors of Newtonian cement grouts with different water cement ratios[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(19): 161-167. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.19.018 http://www.tcsae.org

2020-03-18

2020-09-18

国家自然科学基金（41861134008）；云南省重点研发计划（202003AC10002）；云南省基础研究计划面上项目（202001AT070043）；云南省教育厅科学研究基金（2018JS029）

杨志全，博士，教授，主要从事灾害起动机理与水土保持方面研究。Email：yzq1983816@kust.edu.cn

杨溢，博士，教授，主要从事灾害起动机理与水土保持方面研究。Email：2919847230@qq.com

10.11975/j.issn.1002-6819.2020.19.018

TU 443

A

1002-6819(2020)-19-0161-07