超短期负荷预测中指数平滑法平滑系数的确定方法
2020-12-25郝广涛林清华李晓梅
郝广涛, 林清华, 李晓梅
( 莆田学院 机电工程学院, 福建 莆田 351100 )
0 引言
电力系统能量管理系统的超短期负荷预测是经济调度、 安全分析、 电压控制等的基础[1]。 指数平滑法由于简单可靠、 模型表达清晰等优点,被应用于电力系统超短期负荷预测等领域[2]。
超短期负荷预测的目标是追求高精度水平,而平滑系数是影响指数平滑法预测模型精度水平的主要参数。 对此国内外电力科学爱好者提出了多种平滑系数确定方法, 如分段法[3-4]、 动态调整法[5]、 多模型融合法[6]、 自适应法的改进方法[7-9]。 然而, 上述方法是针对特定的历史数据获得的。 实际上, 对于不同的历史数据, 获取的平滑系数不同, 由此预测的精度、 误差也不同,并且该过程呈现随机性。 由此, 寻找一种普适通用的平滑系数确定方法就显得尤为必要。
此外, 传统平滑系数确定方法主要是以一种误差作为依据评判平滑系数的优劣, 具有片面性。 对此, 本文以统计学中常用的4 种误差评判指标相互佐证确定平滑系数, 并以其中的最小值寻找最优平滑系数。
1 指数平滑法
指数平滑法是1959 年由美国统计学专家布朗提出一种时序数据趋势预测的分析方法[10],目前主要有一次指数平滑法、 二次指数平滑法、三次指数平滑法3 种。
1.1 一次指数平滑法
一次指数平滑法以式(1)表示:
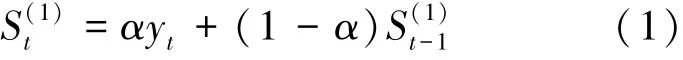
根据式(1), 有如下的迭代:
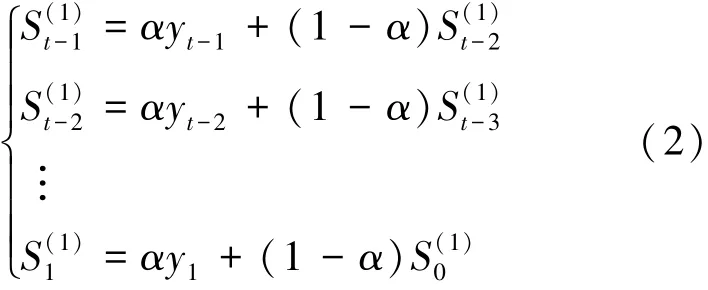
将式(2) 代入式(1), 得:

根据式(3) 可以得到递推公式, 如t - 1 时刻的一次指数平滑公式为:

根据式(3) 和式(4) 可得到, 一次指数平滑法主要用于预测趋势近乎没有变化的时间序列数据,预测模型为:
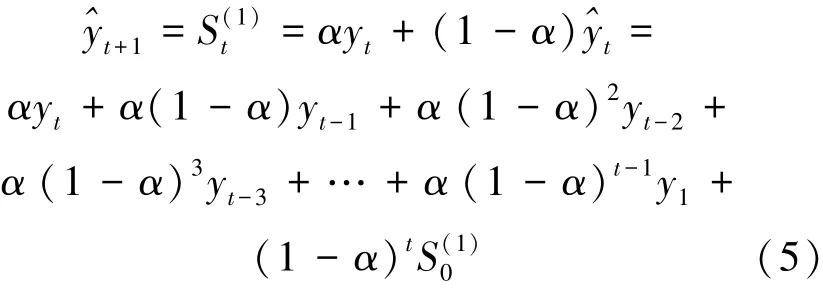
式(5) 中: ^yt+1表示t + 1 时刻的预测值, 等于t时刻的一次指数平滑值表示t 时刻的预测值, 等于t - 1 时刻的一次指数平滑值
由式(5) 预测模型可见: 假设当前时刻是t, 那么对于未来t + 1 时刻的预测值, 是由当前时刻t 以及历史时刻t - 1, t - 2, …, 1 实际值加权形成, 并且权值依次减小。
1.2 二次指数平滑法
二次指数平滑法是在一次指数平滑公式基础上, 再次进行一次平滑得到, 以式(6)表示:
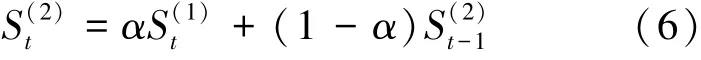
根据式(6), 可以得到如下迭代公式:
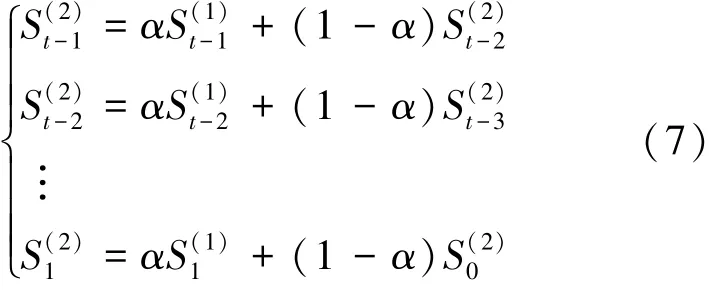
将式(7) 带入式(6) 中, 得:
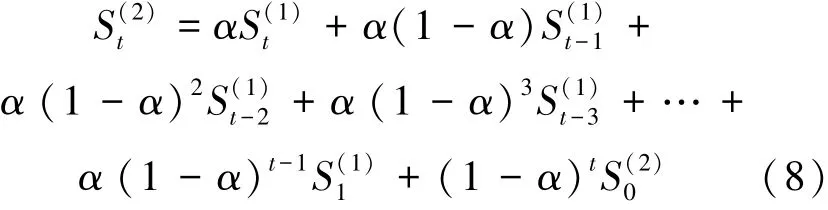
观察式(8) 与式(3) 可以发现, 二者具有相似的形式。
将式(3) 及其递推式(4) 代入式(8) 化简得:
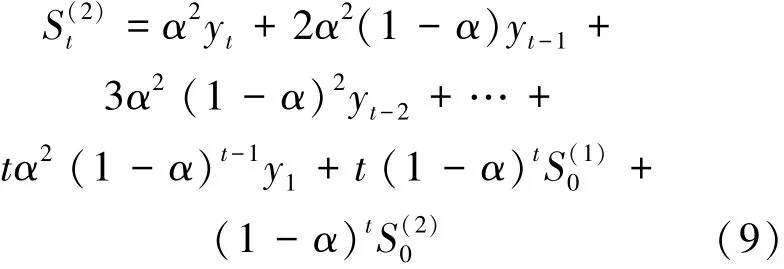
根据式(9) 可以得到二次指数平滑法的递推公式, 如t - 1 时刻的二次指数平滑公式为:

二次指数平滑法通常用于具有线性变化趋势的数据预测, 其单步预测模型如下:
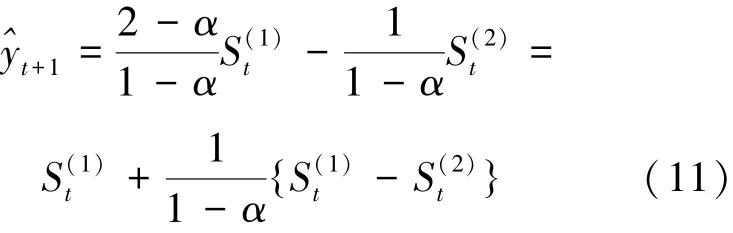
将式(3)和式(9)代入式(11)中, 得:

由式(12) 可见, 右侧的系数逐步变小, 具有明显的规律性。
1.3 三次指数平滑法
三次指数平滑法是在二次指数平滑法的基础上, 再次进行平滑得到, 以式(13)表示:

根据式(13), 可以得到迭代递推公式:

将式(14) 代入式(13) 中, 可得:

将式(9)及其递推公式(10)代入式(15), 得:
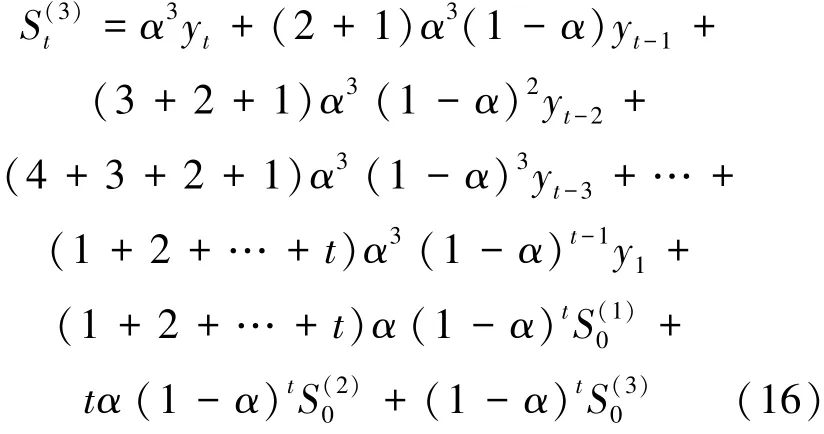
三次指数平滑法主要用于具有非线性变化趋势的数据预测, 其单步预测模型为:

将式(3)、 式(9)、 式(16) 代入式(17), 化简得到结果显示: 三次指数平滑法预测模型中的系数均为高次, 系数规律不明显。
2 误差评价指标
在电力系统超短期负荷预测中, 常用的误差评价指标有均方根误差、 平均绝对值误差、 平均绝对百分比误差、 平均平方和误差[11]。
各种误差评价指标各有优势, 本文取4 种误差评价指标中最小的一种予以确定平滑系数。
2.1 均方根误差
均方根误差( root mean square error,RMSE)表示预测值偏离实际值之间的程度。 RMSE 越小, 表示预测值越接近实际值, 以式(18)表示:
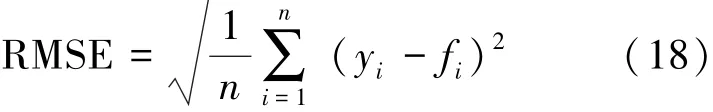
式(18) 中: yi表示第i 个实际值, fi表示第i 个预测值, n 表示个数。
2.2 平均绝对误差
平均绝对误差(mean absolute error, MAE)是预测值与实际值之间绝对误差的算术平均值,以式(19)表示:
式(19) 中, yi、 fi和n 含义与式(18) 相同。
2.3 平均绝对百分比误差
平均绝对百分比误差(mean absolute percentage error,MAPE)由MAE 发展而来, 是一个相对值, 表示预测值与实际值之间绝对误差与实际值比值的算术平均值, 以式(20)表示:
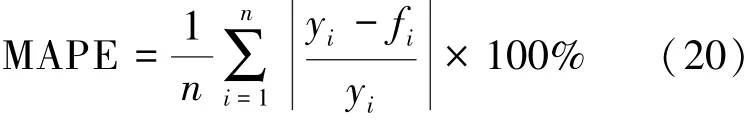
式(20) 中, yi、 fi和n 含义与式(18) 相同。
2.4 均方误差
均方误差(mean squared error, MSE) 是预测值与实际值之差平方的平均值。 MSE 通常表示数据的变化程度, MSE 越小, 说明预测模型具有更高的精度, 以式(21)表示:
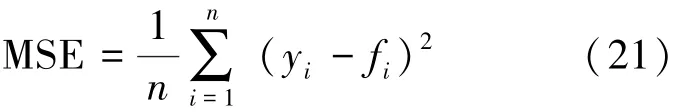
式(21) 中, yi、 fi和n 含义与式(18) 相同。
3 确定平滑系数
本文是在历史数据较多(大数据)的环境下,开展一次指数平滑法预测模型、 二次指数平滑法预测模型、 三次指数平滑法预测模型的研究。
通常来说, 若用于预测的历史数据较多, 则一次指数平滑法预测模型式(5)、 二次指数平滑法预测模型式(12)、 三次指数平滑法预测模型式(17) 中的初始值S(1)0、 S(2)0、 S(3)0对于预测的影响较小, 均取原始序列的第一个数据即可。 由此, 影响一次指数平滑法预测模型、 二次指数平滑法预测模型、 三次指数平滑法预测模型精度的主要因素就是确定其相同的平滑系数α。
而若要确定式(5)、 式(12) 和式(17) 预测模型中的平滑系数α, 需要依据不同的误差评价指标, 即以RMSE(式(18))、 MAE(式(19))、MAPE( 式(20))、 MSE( 式(21)) 确定平滑系数α。
设用于预测的n 个历史负荷数据序列D 为:
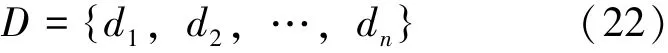
式(22) 中, d1, d2, …, dn为时间由远及近的负荷数据。
以D 中的m(m <n) 个连续数据元素作为历史数据输入, 以较小的平滑初始值α0= ζ 计算紧随其后的第m + 1 个负荷预测值^ym+1, 并将其与实际值ym+1的差值作为误差:
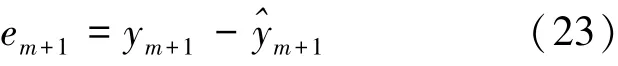
对D 中剩余的数据元素按照式(23) 依次进行计算, 得到n - m 个误差序列E:

将式(24) 中的误差代入式(18) ~式(21)中依次获得平滑系数α0对应的RMSEα0、MAEα0、 MAPEα0、 MSEα0, 以ζ 为步长, 在α ∈(0, 1) 区间内依次计算α1= α0+ ζ, α2= α0+2ζ, … 对应的误差序列:
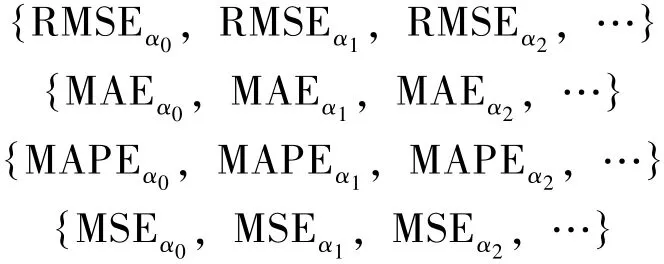
进一步可以求出各种误差评价序列最小值, 及其对应的平滑系数:

选取式(25) ~式(28) 中评价模型误差最小的,对应的平滑系数作为将采用的平滑系数。
4 算例分析
采用不同的误差评价指标分别对一次、 二次、三次指数平滑法的预测模型进行预测结果评价。
采用某实际变电站某年6 月至9 月间的91 d, 每天24 h, 每0.5 h 采集一次负荷数据, 对上述结果进行验证。 由于采取的历史数据较多,S(1)0、 S(0)2、 S(0)3均取原始序列的第一个数据。
由于平滑系数α ∈(0, 1), 给定一个较小的初始值α0= 0.001 和步长ζ = 0.0001 进行4 种误差评价标计算, 计算结果如下。
4.1 一次指数平滑预测模型
经过RMSE、MAE、MAPE、MSE 四种误差评判指标计算,结果分别如图1、图2、图3、图4 所示。
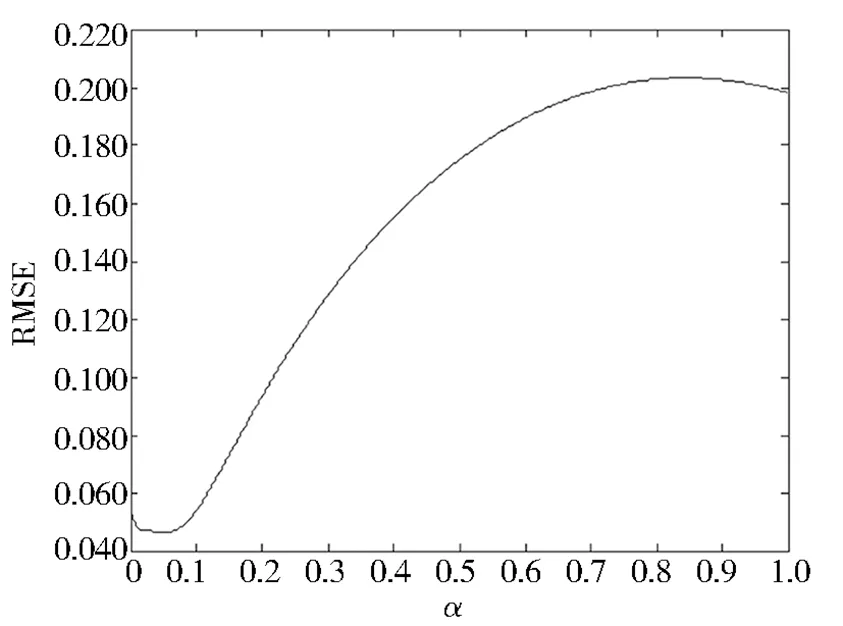
图1 RMSE 计算结果
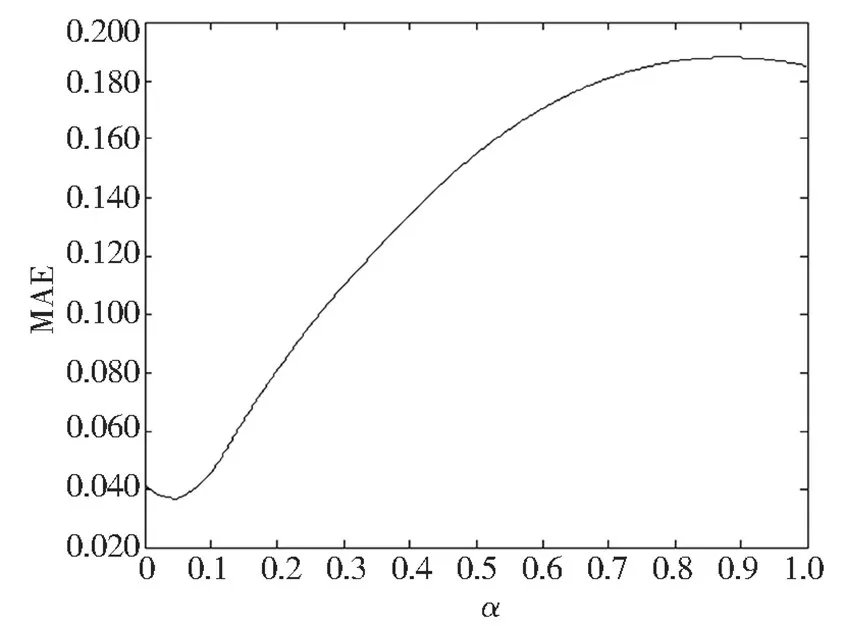
图2 MAE 计算结果
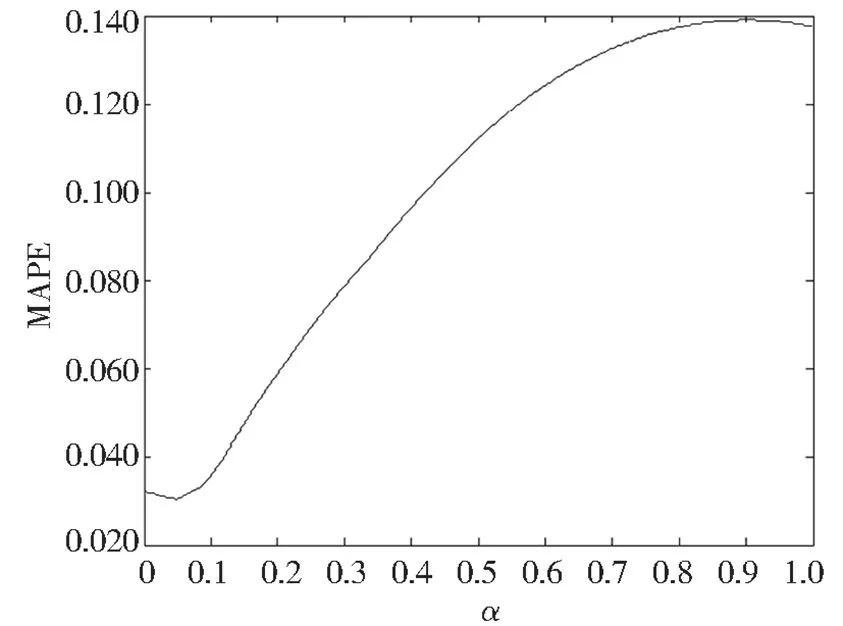
图3 MAPE 计算结果
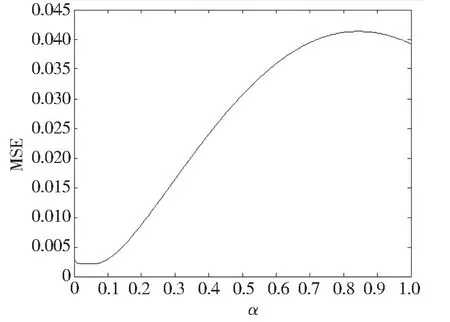
图4 MSE 计算结果
经过计算, 可以获得图1 ~图4 中的最小值及其对应的平滑系数, 如表1 所示。

表1 4 种误差指标对应的平滑系数
4.2 二次指数平滑预测模型
使用RMSE、 MAE、 MAPE、 MSE 四种误差评判指标对二次指数平滑预测模型进行计算, 结果分别如图5、 图6、 图7、 图8 所示。
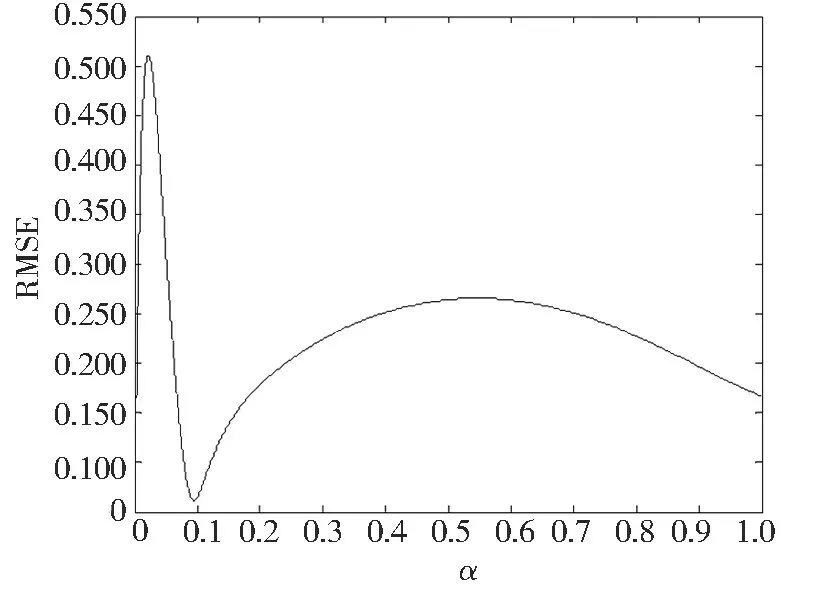
图5 RMSE 计算结果
经过计算, 可以获得图5 ~图8 中的最小值及其对应的平滑系数, 如表2 所示。
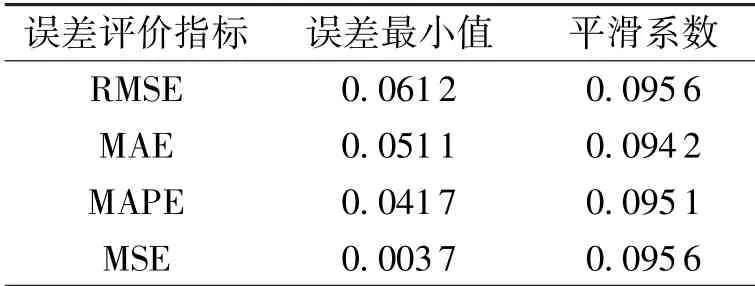
表2 4 种误差评判指标对应的平滑系数

图6 MAE 计算结果
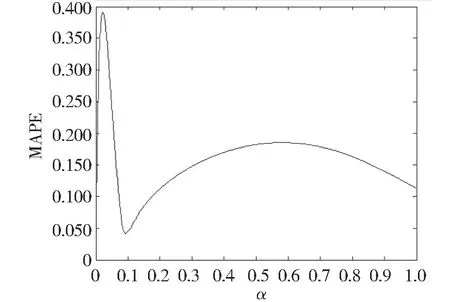
图7 MAPE 计算结果
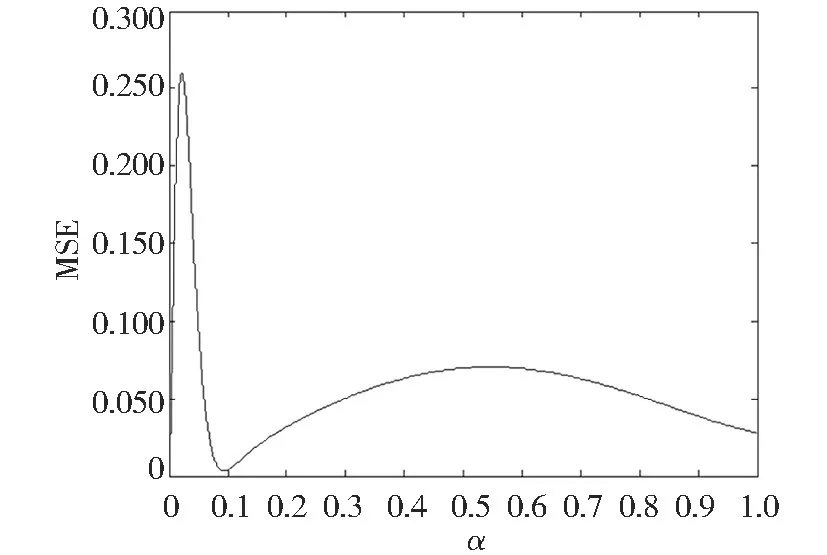
图8 MSE 计算结果
4.3 三次指数平滑法预测模型
使用RMSE、 MAE、 MAPE、 MSE 四种误差评价指标对三次指数平滑法预测模型进行计算,结果分别如图9、 图10、 图11、 图12 所示。
经过计算, 可以获得图9~图12 中的最小值及其对应的平滑系数, 如表3 所示。
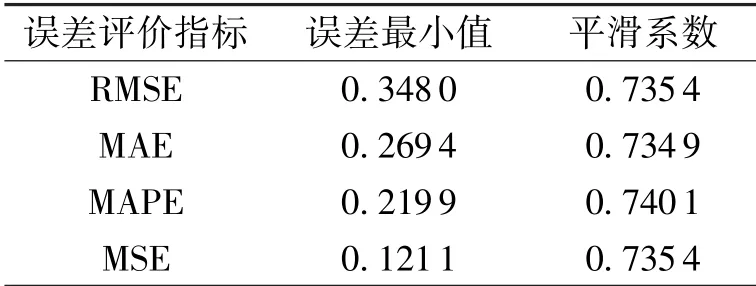
表3 4 种误差评判指标对应的平滑系数
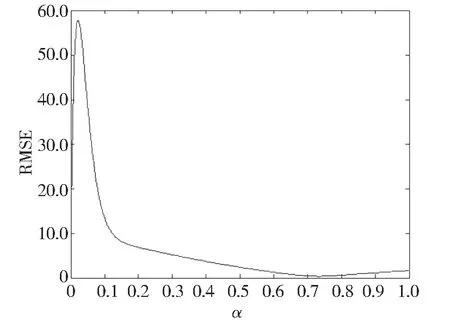
图9 RMSE 计算结果
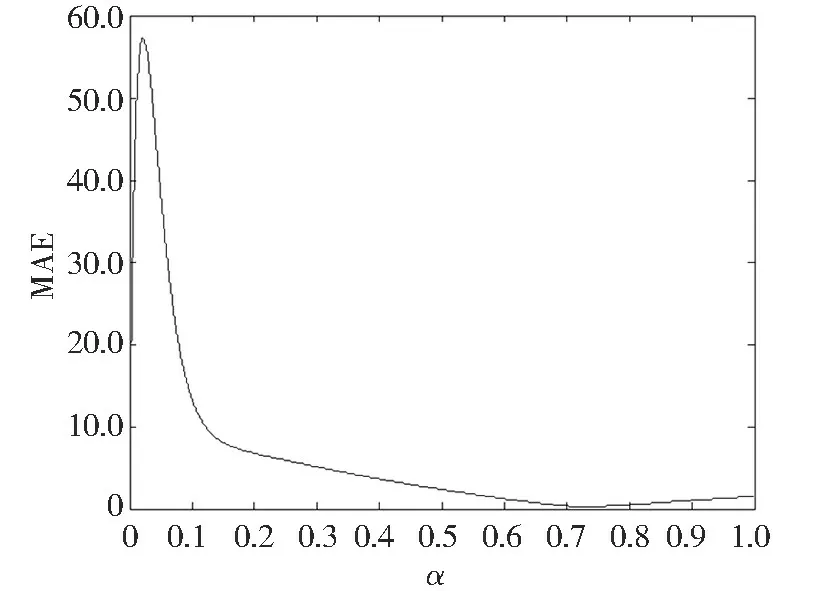
图10 MAE 计算结果
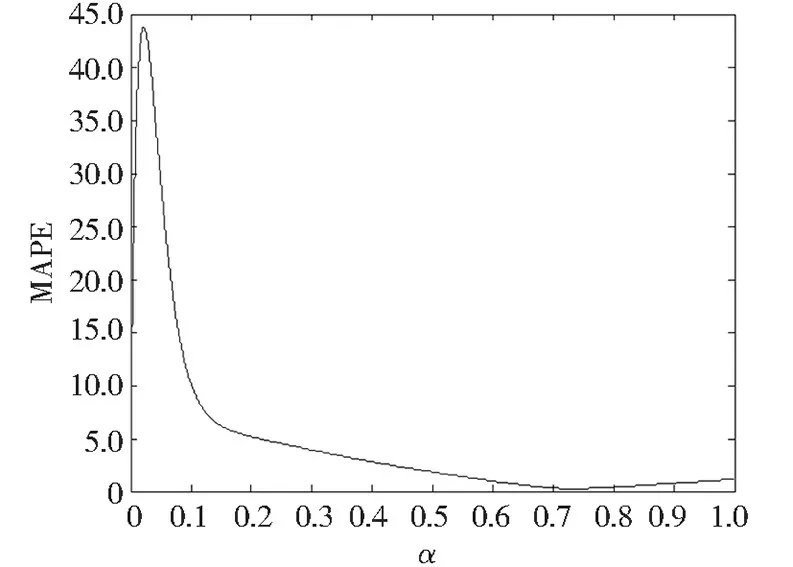
图11 MAPE 计算结果

图12 MSE 计算结果
4.4 比较分析
上述4.1 节~4.3 节用于一次、 二次、 三次指数平滑法预测模型的部分历史负荷数据如图13 所示。
由图13 可以看出, 该历史负荷数据具有非线性特性, 因此采用三次指数平滑法预测模型。进一步由表3 对应平滑系数列可以看出, 平滑系数都在0.735 4 附近, 以误差最小为原则, MSE对应的误差最小, 因此选用进行三次指数平滑法预测模型进行预测, 预测结果如图14 所示。 由图14 可见, 负荷预测精度水平较高, 误差在1%~2%。

图13 部分历史负荷数据
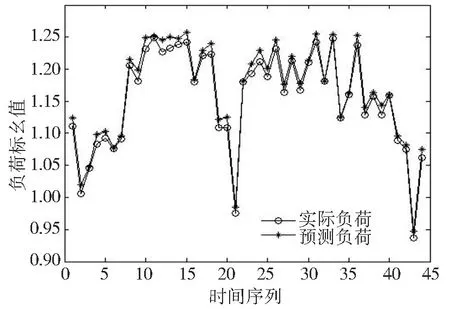
图14 负荷预测结果
5 结论
为了提高指数平滑预测模型的精度, 提出了一次、 二次、 三次指数平滑预测模型平滑系数的求解方法, 并通过实际算例予以验证, 结果表明: 1) 在平滑系数区间内进行逐次搜索求解误差最小值是可行的; 2) 三次指数平滑预测模型用于预测非线性趋势的负荷数据精确度较高;3) 多种误差评价指标相互印证确定平滑系数具有较高的可信度。
