基于径向基神经网络的废旧铝分离技术研究

周晏锋，陈蔚芳,潘立剑，韦子祥，徐鹏行

(南京航空航天大学机电学院，江苏 南京 210016)

0 引言

随着现代工业的快速发展，铝合金由于密度小、强度大、适应性强和可回收等优良特性被广泛用于各个领域[1-2]。每年进行铝矿开采，同时又有大量废旧铝产生，对环境产生了巨大的破坏，所以有必要进行废旧铝分选研究。分选指对不同种类的废旧铝进行识别并分类，最后把它们分离的系统。回收来的废旧铝来自不同领域，必然是多种牌号混杂。对不同牌号的废旧铝进行精细分选，可以简化后期的回收处理流程，帮助企业降低成本。目前，常用的金属分选系统主要根据金属的密度、颜色、磁性和导电性等物理特性进行分选，如浮选法、电涡流法等[3-4]。由于不同牌号的废旧铝物理特性非常接近不易区分，此类方法不适用于废旧铝的精细分选。

激光诱导击穿光谱(LIBS)技术是通过激光打在样品上产生瞬态等离子体，然后对光谱进行分析，从而实现对样品定性定量分析的光谱技术。自20世纪60年代被提出后，已被广泛应用于多个领域[5-7]。基于此技术，可以根据成分实现不同牌号废旧铝的精细识别与分类。现有的分离方式主要有喷气式、翻板式和机械手[8]。袁华昕[9]使用X射线对煤和矸石进行区分，设计了算法获取尺寸信息，最后利用喷气气流将二者分离。谭春超[10]则是采用图像技术对煤和矸石进行识别，利用机械手进行分离操作。王祺奥等[11-13]使用双能X射线透射废金属进行种类识别，并设计了喷气模块将不同金属分离开。邓继忠等[14]先用视觉技术对农产品识别分类，再控制电机带动翻板运动实现分离目的。机械手过于昂贵，成本较高，而现有的喷气式与翻板式技术1次只能分离2种物料，想实现多种物料分离则需要进行多级分离，增加了硬件成本。

想要一次性分离多种废旧铝，将相同种类的废旧铝吹至一处，就需要根据废旧铝物料的体积参数准确调整喷气模块的气压，即气压、体积与吹离的距离存在一定的函数关系。由于分离时气流作用于废旧铝的情况不易获取，此函数关系难以直接建立数学模型，而径向基(radial basis function，RBF)神经网络可以较好地逼近连续函数[15]。本文通过实验记录数据获得训练集和测试集，建立RBF神经网络模型，并对预测效果进行测试。基于RBF模型预测结果，根据废旧铝物料的体积自适应地调整喷气气压，系统可以将不同种类的废旧铝吹至不同的距离，实现废旧铝的分离目的。

1 基本原理

将不同大小的同种废旧铝物料吹至一处，需要根据物料自身特征自适应调整分离装置，即存在函数关系，但此函数较为复杂，难以直接列出。鉴于RBF神经网络可以无限逼近连续函数的特点，可以用于分离系统的控制。RBF神经网络为前馈网络，是一种3层神经网络，其网络结构如图1所示，包括输入层、隐层和输出层。输入层由一些感知单元组成，它们将网络与外界环境连接起来；第2层是网络中仅有的1个隐层，它的作用是从输入空间到隐层空间之间进行非线性变换，在大多数情况下，隐层空间有较高的维数；输出层是线性的，它为作用于输入层的激活模式提供响应。

图1 RBF神经网络结构

径向基函数是一个取值仅依赖于离原点距离的实值函数，即

Φ(x)=Φ(‖x‖)

(1)

或者还可以是到任意一点c的距离，c点称为中心点，也就是

Φ(x,c)=Φ(‖x-c‖)

(2)

任意一个满足式(1)特性的函数Φ都叫做径向基函数，最常用的径向基函数是高斯核函数，形式为

(3)

xc为核函数中心；σ为函数的宽度参数，用以控制函数的径向作用范围。RBF网络中，x=[xi]T为网络的输入，网络的隐含层输出为h=[hj]T，hj为隐含层第j个神经元的输出:

(4)

RBF网络权值为

w=[w1,…,wm]T

(5)

RBF网络输出为

y(t)=wTh=w1h1+w2h2+…+wmhm

(6)

在MATLAB软件中，newrbe()函数可以快速设计一个径向基函数网络，且使得设计误差为0。使用方法为net = newrbe(P,T,spread)，其中,P为输入，T为输出，net为建立的网络。spread值用以调整径向基函数的宽度，宽度为0.832 6/spread。spread值的设置决定了每个径向基神经元对输入向量产生响应的区域。

2 实验部分

2.1 实验装置

废旧铝分离系统的总体设计如图2所示，废旧铝置于传送带上匀速前进。首先经过LIBS模块，由脉冲激光器(北京镭宝公司，Dawa-100)和光谱仪(Avantes，AvaSpace-ULS2048CL-4-EVO)组成。高能脉冲激光照射废旧铝物料后在表面产生等离子体，利用光谱仪对等离子体进行识别确定废旧铝物料的成分，将数据传输至计算机后结合主成分分析法和智能算法对其分类，归类为成分最相近的一类铝合金。接着，物料被线激光轮廓传感器(LMI Technologies，Gocator 2400 series)扫描后，将信息传输至计算机并对物料的体积和形心位置进行计算，最后将控制信息通过串口发送给下位机。

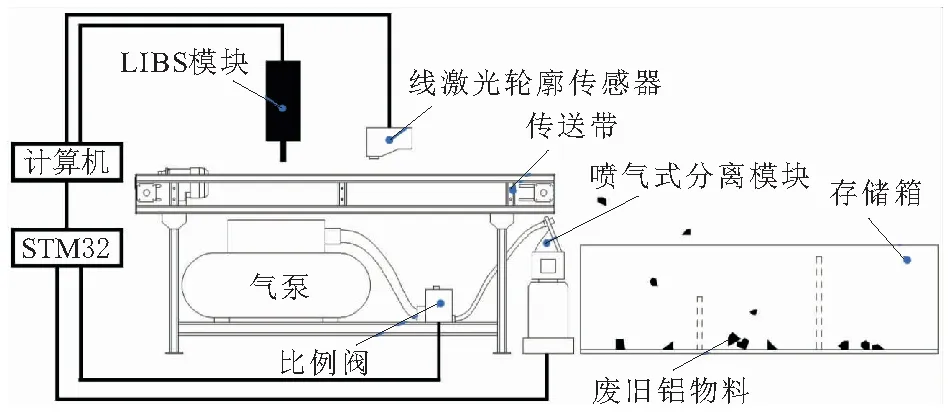
图2 分离系统总体设计

下位机STM32主要用于控制比例阀和喷气模块。比例阀可以按输入的电气信号连续地、按比例地对气压进行调整。喷气模块为自行设计，其具体结构如图3所示。系统有2个步进电机，电机1可以通过联轴器控制喷嘴绕X轴进行俯仰角度调整，用以找到最合适的喷气角度，尽量利用较小的气压实现物料分离；电机2则可以控制喷嘴绕Y轴进行旋转角度调整，主要用以适应物料在传送带上不同位置的情况。根据之前获得的物料形心坐标，对角度进行微调后可以使分离气流对准物料形心，避免漏吹现象，提升分选的准确率。

图3 喷气模块结构示意

最终，每当废旧铝物料通过传送带时，计算机就能获取其种类、体积和形心位置信息，且通过下位机控制后产生一股气压、角度自适应的气流，在物料到达传送带末端落下时，这股分离气流可以将物料吹离预定的距离。存储箱内用挡板分隔有若干空间，则传送带上的物料就可以根据其种类不同被吹到对应的隔间内，实现废旧铝的分离。

2.2 数据获取

使用喷气方式分离废旧铝时，吹离的距离受废旧铝物料的密度ρ、体积V和喷气气压p等参数影响。由于本文主要针对废旧铝进行分离，常见牌号铝合金的密度如表1所示。各系列铝合金密度相差不大，故而只考虑物料体积和气压造成的影响。

表1 常见牌号的铝合金密度

3 结果分析

newrbe函数中的spread为径向基函数的扩展速度，spread值的选取会影响RBF模型的精度和稳定性。因此，选取不同大小的spread值建立模型后，对80组测试集数据进行预测，并与实际值比较从而选取最佳的spread值。不同spread值对应的拟合优度R2(coefficient of determination)和均方根误差分别如图4和图5所示。决定系数R2，也称判定系数或者拟合优度，它是表征回归方程在多大程度上解释了因变量的变化，或者说方程对预测值的拟合程度如何。R2的值越接近1，说明回归方程对预测值的拟合程度越好；反之，R2的值越小，说明回归方程对预测值的拟合程度越差。均方根误差是用来衡量预测值同真值之间的偏差，均方根误差越小则说明预测效果越好。当spread值为0.6时拟合优度最高，之后随着spread值增大趋于稳定，而spread值为0.1～0.2时均方根误差快速降低，之后均处于较低水平。因此，可以得知spread值为0.6时对模型建立最合适，能够得到精度较高的RBF网络模型。

图4 不同spread值下模型的拟合优度

图5 不同spread值下预测结果的均方根误差

取spread值为0.6后，建立RBF网络模型并对测试集进行预测。图6为废旧铝物料吹离距离的分布散点图，其中，图6a为训练集中230组数据的实际距离，图6b为测试集中80组数据的预测距离。可以发现随着物料体积的增大，物料被吹离的距离逐渐减小；而随着分离气流气压增大，吹离距离也在增大。测试集中预测值变化基本符合这一规律，数据的分布规律也基本相似。

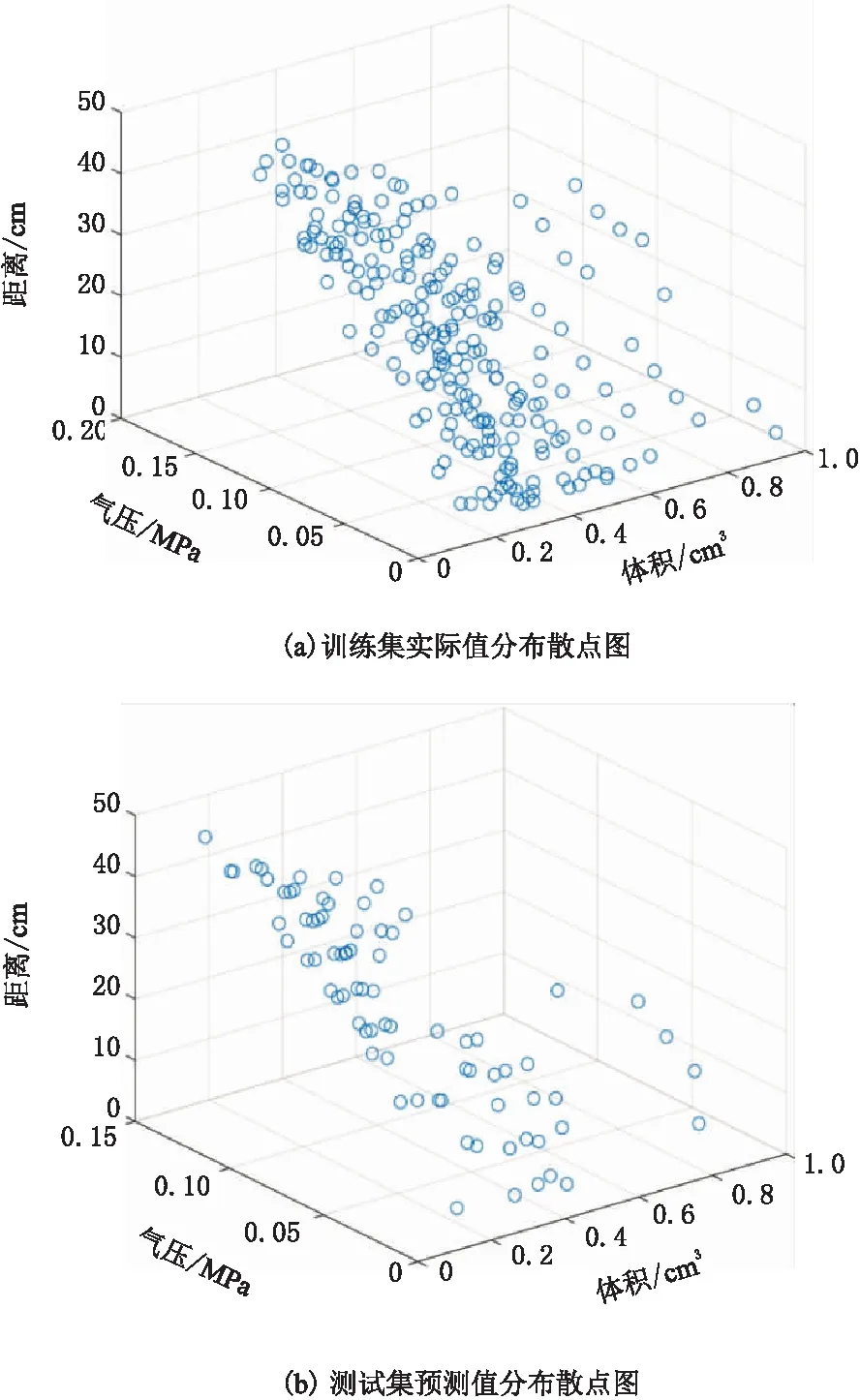
图6 废旧铝吹离距离分布散点图

将这80组数据中吹离距离的实际值和预测值进行对比，如图7所示。预测值的分布基本与实际值相吻合，误差较小。拟合优度R2可达到93%，均方根误差ERMSE约为2.99，证明模型的预测效果较好。分离系统运作时，系统可根据废旧铝具体情况先进行吹离距离的预测，若是预测结果符合预定范围，则选取合适大小的气压进行分离。由于废旧铝的存储部分用隔板进行了空间划分，所以实际分离过程中废旧铝物料只要能掉入正确的隔间内即可，这就使得实际吹离距离的允许误差范围增大，提升了分离系统的容错率，废旧铝的分离效果进一步提升，准确率可以达到96%以上。

图7 RBF神经网络预测结果

4 结束语

本文设计的废旧铝分离系统能够对传送带上废旧铝物料识别，获取其种类、体积和形心位置信息。选取废旧铝物料进行实验并记录数据，建立了吹离距离与气压、体积的RBF网络模型，拟合优度可达93%，均方根误差仅为2.99，实际分离准确率可达96%以上。通过实验，证明系统可以对物料吹离距离进行有效预测，从而选取合适的气压进行自适应分离，提供了一种废旧铝分离的新方法。实验过程中也发现气流没有对准物料会产生漏吹现象，或者物料偏离正常轨迹，此外实际效果也与物料形状有一定关系，值得进一步研究，以提升分离准确率。