基于旋滚比的电主轴轴承预紧力优化研究

闫 轩，许 涛,2，曾柄杰

(1.西安工程大学机电工程学院，陕西 西安 710600；2.西安市现代智能纺织装备重点实验室，陕西 西安 710600)

0 引言

高性能电主轴是目前高端数控机床核心动力部件。“中国制造2025”将提升工业核心功能部件质量、寿命和可靠性作为国家战略任务之一。滚动轴承作为支撑部件是电主轴功能部件的重要组成部分，具有质量可靠、机构简单和便于维护等优点[1-4]。滚动轴承动态力学性能严重影响电主轴运行状况，进而影响数控机床在复杂工况下的加工精度。轴承预紧技术对电主轴高精度和高速度运行具有决定性作用，是高速电主轴核心技术之一[5-6]。轴承预紧力过大会导致轴承温升和磨损加快，降低轴承寿命，而轴承预紧力过小又会导致电主轴刚度降低，无法稳定运转。适当的轴承预紧力可使主轴准确定位，提高电主轴寿命、刚度和运转精度。因此，合理的轴承预紧力对于电主轴综合性能的提升具有重要意义[7]。

轴承预紧力一直是国内外学者的研究热点，日本研究者Hirano在1965年做了大量实验，研究了多种工作条件下球轴承的打滑情况，最终从实验结果中推导出球轴承打滑阈值[8]，确定不同工况下轴承所需最佳预紧力。打滑条件也为确定轴承预紧力标准提供一种可行思路[9]。旋滚比是反映球轴承高速状态的重要参数，是滚动体在套圈轨道接触处自转角速度和滚动角速度比值。在不出现打滑情况下，旋滚比越大，滚动体磨损和发热越严重。球轴承在高速状态下旋滚比要尽可能低[10]。因此用旋滚比优化轴承预紧力方案可行性较高。

目前，对于轴承预紧力确定很难给出能适用多种工况的理论解。Hirano[8]给出的轴承打滑阈值为轴承预紧力确定提供了可行路径。本文建立了优化轴承预紧力模型，以Hirano[8]的阈值为优化标准，采用轴承旋滚比优化高速状态下轴承预紧力。

1 角接触球轴承动态力学模型

角接触球轴承滚动体在高速状态下，受离心力影响使得轴承动力学特性发生变化，进而影响电主轴系统动力学。Jones[11]以轨道控制理论为基础建立球轴承拟静力学分析模型。本节基于Jones[11]的轨道控制理论，建立以旋滚比优化轴承预紧力的轴承动力学模型。模型建立过程如图1所示。

图1 建立模型流程

1.1 高速状态下滚动体载荷分析

角接触球轴承在高速运转时，滚动体受到离心力和陀螺力矩影响导致轴承内部受力发生改变。本节建立一种考虑离心力和陀螺力矩的轴承动态力学模型，来描述高速状态下轴承内部载荷变化规律。分析轴承在运转过程中，滚动体由于离心力和陀螺力矩作用,而导致的滚动体与轨道接触处力学分布、相对变形和内外轨道接触角的完整变化规律。角接触球轴承单个滚动体受力情况如图2所示。

图2中，Fa为轴承预紧力；Fr为轴承径向载荷；Fc为离心力；αi和αo分别为内外轨道实际接触角；Qi和Qo分别为外滚动体与内外轨道的相互作用力；Ti和To分别为滚动体与内外轨道切向摩擦力；Mg为陀螺力矩。Fc、Qi和Qo可由如下公式计算[9]：

Fc=π3dmρD3n3/10 800

(1)

(2)

(3)

dm为轴承节圆直径；ρ为滚动体密度；D为滚动体直径；n为轴承转速；Ki和Ko分别为内外轨道载荷-位移常数；δi和δo分别为滚动体与内外轨道接触区变形量。

为保证轴承高速运转中滚动体能够平稳运行，图2a中预紧力Fa、滚动体与外轨道相互作用力Qo和轴承径向载荷Fr三力需满足三角形准则，因此，滚动体受力需满足如下条件[12]：

Fa=Qosinαo

(4)

Fr=Qocosαo

(5)

由式(1)～式(5)可知，角接触球轴承预紧力与内外轨道接触角和离心力密切相关。其中，离心力变化主要由于速度改变，接触角变化也是由于轴承转速增加。因此，在高速状态下载荷分析中，转速和预紧力不可忽视。为保证轴承系统能够正常运行，预紧力需与转速共融匹配。

1.2 摩擦磨损机理

当轴承处于无载荷状态下，内外轨道曲率中心距离为BD，且BD=ri+ro-D(ri为内轨道曲率半径，ro为外轨道曲率半径)。在轴向载荷作用下，内、外轨道曲率中心之间将出现接触变形δi和δo，且随着轴向载荷的增加而增大，如图3a所示。图3b为轴承每个滚动体相对角位置，即滚动体方位角。

图3 静载荷作用下不同位置滚动体-轨道接触

角接触球轴承在回转过程中，会出现离心力作用在滚动体上导致滚动体与内外轨道接触角不同现象，导致内外轨道曲率中心之间连线不再与BD共线，而成为一条折线，如图4所示[13]。根据Jones的外轨道控制理论，假设外轨道曲率中心在离心力与载荷联合作用时保持不变，内轨道曲率中心位置发生改变，导致滚动体中心位置也发生改变[11]。在滚动体任意方位角j处，滚动体中心最终位置与外轨道曲率中心距离为

Δoj=(fo-0.5)D+δoj

(6)

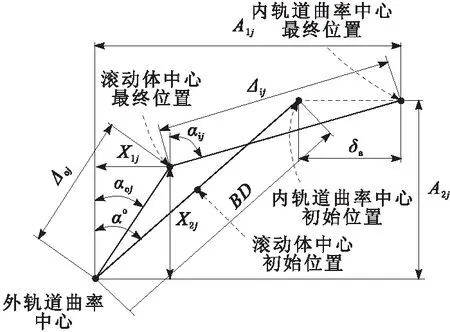
图4 载荷作用后滚动体中心和轨道曲率中心示意

同理，滚动体中心与内轨道曲率中心最终位置距离为

Δij=(fi-0.5)D+δij

(7)

其中，fi和fo计算方法为

(8)

当角接触球轴承只受轴向预紧力作用时，轴承内、外轨道之间会产生轴向位移δa，如图4所示。在滚动体任意方位角处，内、外轨道曲率中心轨迹轴向和径向距离分别为

(9)

为了便于分析，在图4中引入新的变量X1和X2，在滚动体任意方位角处，有

(10)

根据勾股定理可得

(11)

据图2c所示滚动体受力情况，可得平衡方程为

(12)

其中，切向摩擦力T计算方法如下：

T=Mgj/D

(13)

(14)

(15)

(16)

为方便求解方程组(12)，需建立轴承轴向平衡条件：

(17)

Z为角接触球轴承滚动体个数。在使用Newton-Raphson[14]法计算出每个轴承滚动体X1j、X2j、δij和δoj，并确定离心力Fc和陀螺力矩Mgj后，联立式(10)～式(17)组成方程组。使用数值迭代法求得αi和αo的解。

1.3 角接触球轴承滚动体打滑准则

在高速状态下，轴承滚动体由于离心力作用导致滚动体与内轨道赫兹接触面积随转速增加而减小[8，12-13]。此时，滚动体打滑效应因接触面积减小而增加。当转速到一定数值后，滚动体会与内轨道完全隔离，出现打滑现象。滚动体打滑会引起摩擦增加，不利于整个回转系统工作[9]。因此，电主轴预紧力将直接影响轴承内部摩擦状态。Hirano[8]针对轴承滚动体打滑效应在不同工况下进行多次试验研究，最终推导出轴承打滑阈值：

(18)

在确定轴承参数和转速后，根据图5所示算法并将该阈值作为约束条件，即可计算出合适的预紧力。

图5 数值迭代法流程

2 滚动体轨道和自旋速度分析

(19)

图6 滚动体角速度矢量分解示意

(20)

(21)

假设滚动体与轨道接触处没有滑动，则有：

(22)

(23)

将同样的方法应用于外轨道，可得到滚动体自旋速度ωb大小的另一个表达式为

(24)

γ′=D/dm,γi=D·cosαi/dm，γo=D·cosαo/dm。β为轴承滚动体姿态角，计算方法为

(25)

联立式(23)和式(24)，可得到滚动体轨道速度ωc和自旋速度ωb，即

(26)

假设滚动体相对于内轨道角速度ωbi与CiO1共线，且O1为相对速度瞬心点。ωbi应为接Ci触点处内轨道相对于保持架角速度与滚动体角速度的差，即

ωbi=ωb-(ωi-ωc)

(27)

同理，在接触点Co处，滚动体相对于外轨道角速度为

ωbo=ωb-(-ωc)

(28)

(29)

则内、外轨道旋滚比(RSRi和RSRo)计算公式为

(30)

3 案例分析

以角接触球轴承B7007C为例，研究滚动体内、外轨道旋滚比与第2节所述阈值之间关系，分析轴承在不同工况下电主轴轴向预紧力优化方法。轴承主要参数如表1所示。

表1 B7007C轴承主要参数

根据该轴承主要参数，以及第1和第2节编写了MATLAB脚本文件，计算轴承旋滚比。图7为滚动体内轨道旋滚比计算结果。由图7可以明显看出，不同速度旋滚比变化趋势一致，同一预紧力下，随着速度增加内轨道旋滚比呈增加趋势。随着预紧力的增加，不同速度下旋滚比逐渐与静止状态下旋滚比曲线重合。

图7 滚动体内轨道旋滚比

图8为内轨道旋滚比随预紧力和转速变化三维图。图8中，黑线代表Hirano发现的阈值，即滚动体打滑临界状态。根据阈值计算内轨道旋滚比大小，再根据旋滚比大小得出对应转速和预紧力值，即优化结果。该条曲线将图像划分为2个区域，即打滑区域和不打滑区域。电主轴在实际运行过程中，轴承预紧效果应达到图8所示不打滑区域，但预紧力过大会使摩擦加剧，加大滚动体与轨道之间磨损。因此，图8中曲线所示优化结果既能保证轴承工作效率，又能最大限度降低轴承内部磨损。

图8 内轨道旋滚比预紧力优化结果

图8中，曲线对应内轨道旋滚比范围为0.12～0.14。内轨道旋滚比处于一个相对稳定状态，因此旋滚比大小可以反映轴承预紧效果。

4 结束语

基于外轨道控制理论，根据角接触球轴承高速运行过程中滚动体打滑状态，结合Hirano发现滚动体打滑阈值，建立了一种以旋滚比优化轴承预紧力动力学模型。数字仿真结果显示：根据打滑状态可以得出角接触球轴承不同转速下最佳预紧力;当轴承处于最佳预紧力下，不同转速和预紧力状态下内滚道旋滚比取值稳定在0.12～0.14之间；本文研究可为实际的工程操作提供理论指导。