空间弱撞击对接机构传递功率分析

陈传志，汪 捷，陈金宝，崔继云，霍伟航，江安澜

(南京航空航天大学航天学院 深空星表探测机构技术重点实验室，江苏 南京 210016)

0 引言

与传统的对接机构相比，配备有机电一体化的弱撞击对接机构(LIDM)具有承载空间大、传递性能好、结构紧凑且对接精度高等优点，属于闭环反馈控制系统，与带有力传感器的电磁捕获环配合实现柔性捕获的异体同构周边式对接系统，其采用的内翻式方案使得追踪飞行器与目标飞行器配有构型一致的对接机构，无主被动之分，是未来中国载人航天、探月工程、深空探测和国际空间站建设最具潜力与应用价值的对接机构之一，广泛应用于空间站及其舱段的对接任务中[1]。

航天对接任务是一项严谨而特殊的任务，对接机构的各类性能指标直接影响到了对接任务的成功与否。国内外众学者针对于对接机构的各类运动、力学性能，以及精度误差等方面进行了相关研究。张玲瑄等[2]研究了弱撞击对接机构在任一位姿下运动灵巧空间内的力学性能；于大泳等[3]探讨了对接机构运动模拟器的机构原始误差和对接过程误差引起的位姿误差；邹恒等[4]分析了一种三指式对接机构的运动学，并给出了以主动端结构紧凑为目标的优化函数；陈传志等[5]将弱撞击对机构的力雅可比矩阵分解为2个分别与力和力矩传递相关的子矩阵，并计算出力和力矩传递性能的分布规律；Salisbury等[6]提出了采用运动雅克比矩阵的条件数作为机器人的灵巧度，用以衡量系统的精度判别；Yoshikawa[7]提出了一种可操作度概念来衡量系统的灵巧性；徐卫良等[8]以公差作为优化目标，分析了工业机器人的精度优化问题。

本文将从全新的传递功率角度出发，分析在捕获阶段中空间弱撞击式对接机构(LIDM)的传递性能，以螺旋理论为基础推导了传递功率的具体表达式。同时，参考相关文献[9]，提出了瞬时能效功率比的概念，研究了在不同工况下工作空间对于空间弱撞击对接机构对接环(LSR)的瞬时能效功率比影响特征，并建立性能评价指标。

1 空间弱撞击对接机构

空间弱撞击式对接机构机械结构如图1所示，主要分为LSR负载对接环系统、驱动臂系统、支撑定位系统和锁合系统。

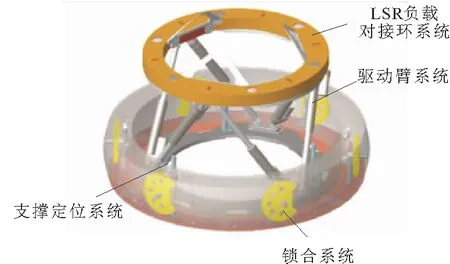
图1 弱撞击对接机构

LSR负载对接环系统的整体框架结构与被动端保持一致，采用同样的中心对称下的导向瓣、定位销孔与电磁捕获装置分布，但是增设了内环与六维力传感器，二者与外环组成了一个六维的力/力矩测量系统，实时将力与力矩信息传输给控制系统。

驱动臂系统包含6根驱动臂，与LSR负载对接环共同组成了1个六自由度并联平台，控制系统通过调整驱动臂长度来控制LSR的位姿信息。驱动臂又称为机电线性制动器，机械结构包含有电机、滚珠丝杠、转动枢轴和套筒等，本质上为一螺杆，该螺杆可以使用电机来进行伸缩。

定位锁合系统包括定位系统与锁合系统。其中，定位系统机械结构包含有撞杆、基座等，功能上是为了避免LIDM在非工作状态下可能发生的晃动损坏；锁合系统包括传动机构、驱动机构和结构锁等，是完成LIDM主、被动端连接、保持与分离的主要操作机构。

2 LIDM捕获系统的传递功率分析

LIDM捕获系统利用控制端操作驱动臂的执行推杆的伸缩量，用以完成LSR的位姿输出，以达到输入端与输出端之间传递运动和力的效能。研究LIDM的运动/力传递功率是用以评判LIDM机构本身优劣的性能指标的重要组成部分。本节以螺旋理论为出发点，通过求解运动螺旋与力螺旋的互易积，来获知系统的传递功率。由于传递功率与LIDM机构本身构型参数、LSR当前位姿信息与速度信息直接相关，不同尺寸构型下的LIDM的传递功率也是不一样的，不能单纯通过传递功率来评价系统的优劣，因此提出瞬时能效功率比的概念，用以评价某一构型LIDM的传递效能。

2.1 螺旋理论求解互易积

螺旋理论是空间机构学中一种重要的数学工具，螺旋理论将研究的目标系统的动力学特征处理为运动螺旋与力螺旋，并拥有其相应的Plücker坐标加以描述。其中，运动螺旋与力螺旋的互易积的概念，其物理意义正是传递功率。

根据螺旋理论，任一刚体在空间中瞬态运动都可以看成是由绕某一旋转轴的转动与沿着该旋转轴方向的平动组成而成。这一瞬态运动规律利用运动旋量加以描述(图2)，表示为

S1=(ω;v)=(ω;r1×ω+h1ω)

(1)

图2 运动螺旋示意

ω为该运动旋量的轴线矢量，这对应刚体正是角速度的表达意义；r1为基座原点到该运动旋量轴线上任一点的矢量；v为该点在基坐标系下的速度；h1为该螺旋的节距，且h1=(ω·v)/(ω·ω)。

特别地，当h1=0时，该刚体瞬态运动表述为纯转动；当h1→时，该刚体瞬态运动表述为纯平动。

类似地，刚体同样有力螺旋的定义(图3)，即

S2=(f;M)=(f;r2×f+h2f)

(2)

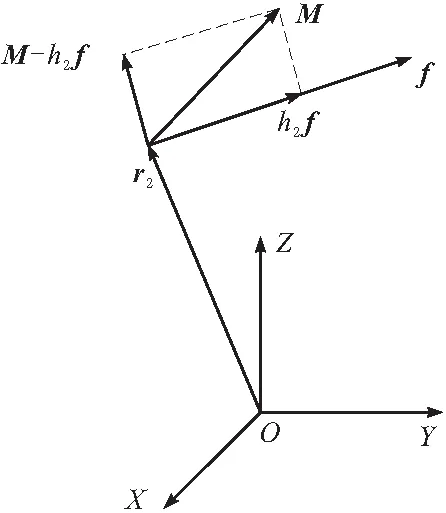
图3 力螺旋示意

f为沿着该轴线方向的力矢量；r2为基座原点到该运动旋量轴线上任一点的矢量；M为该点的转动力矩；h2为该螺旋的节距，且h2=(f·M)/(f·f)。

特别地，当h2=0时，该力螺旋表述为纯力；当h2→时，该力螺旋表述为纯力矩。

综上，运动旋量与力旋量的互易积表述为

S1∘S2=(ω;v)∘(f;M)=

(ω;r1×ω+h1ω)∘(f;r2×f+h2f)=

f·(r1×ω+h1ω)+ω·(r2×f+h2f)=

(h1+h2)(f·ω)+(r2-r1)·(f×ω)=

(h1+h2)cosθ-dsinθ

(3)

θ为运动螺旋与力螺旋的轴线夹角；d为运动螺旋与力螺旋的公垂线长度。互易积的物理意义正是该力螺旋旋量对于该刚体在当前瞬态下的传递功率，可以看到，通过螺旋理论的互易积求解，传递功率转换成空间中运动螺旋与力螺旋轴线的相对几何关系参数。

2.2 传递力旋量

为研究LIDM的传递功率，以各个分支驱动臂作为研究对象，讨论各个分支链对于LSR的传递过程。引入瞬时运动旋量与力旋量，用以描述机构当前运动状态。LIDM拥有6根支链连接基座与LSR，其中任一支链都对LSR提供一个传递力旋量，即

Si2=(fi;Mi)

(4)

由于每根驱动臂支链采用移动副进行驱动的方式，故该传递力旋量表述为纯力，相应的节距h2=0，故式(4)等价于：

Si2=(fi;ri×fi)

(5)

ri为各个驱动臂支链与LSR的铰接点于基座坐标系下的坐标；fi为各个驱动臂的驱动力矢量。这里的驱动力反馈的是准静态下LIDM捕获系统承载能力。

速度雅克比矩阵定义为

(6)

根据虚功原理，力雅可比矩阵是速度雅可比矩阵的转置，则有下式成立：

F=JTf

(7)

F为LSR承载中心处力与力矩在欧拉坐标系下的表示；f为各个驱动臂的驱动力。鉴于需要得到F在基座坐标系下的表示，引入矩阵R，使得

FR=RJTf

(8)

FR为LSR承载中心处力与力矩在基座坐标系下的表示。矩阵R是一个与姿态角相关的矩阵，即

(9)

由此获知准静态作用下的驱动力矩阵f为

f=(RJT)-1FR

(10)

将式(10)代入式(5)，并处理为矢量，对应每一根驱动臂的传递力旋量表述为

(11)

ui为沿着各个驱动臂方向的单位向量。

根据螺旋理论，该传递力旋量的轴线方程为

(12)

2.3 传递运动旋量

为研究LIDM的输入运动旋量，以各个分支驱动臂作为研究对象，讨论各个分支链对于LSR的传递过程中的输入运动旋量。LIDM拥有6根支链连接基座与LSR，其中，任一支链都对LSR提供一个输入运动旋量，即

Si1=(ωi;vi)

(13)

不考虑驱动臂执行推杆绕自身轴线的转动，根据系统运动学关系可以推导得

(14)

v0与ω0为LSR的速度信息；ui与li为第i根驱动臂的单位向量与杆长；R为对应LSR的旋转矩阵。

传递运动旋量的节距表述为

hi1=(ωi·vi)/(ωi·ωi)

(15)

根据螺旋理论，该传递力旋量的轴线方程为

v0+ω0×Rai-

(16)

由于建模假设中不考虑驱动臂执行推杆绕自身轴线的转动，存在下式成立：

ωi·vi=0

(17)

将式(17)代入式(15)，可知此时节距为

hi1=0

(18)

此时传递运动旋量在瞬态下表述为一个纯转动，式(16)的轴线方程化简为

v0+ω0×Rai

(19)

2.4 传递功率求解

力螺旋旋量对于该刚体在当前瞬态下的传递功率可通过螺旋理论的互易积求解，且由前文可知，传递功率转换成空间中运动螺旋与力螺旋轴线的相对几何关系参数，由此传递功率的求解转换为一个纯数学问题。这里不再赘述，直接给出求解结果。根据式(12)与式(19)将直线方程处理为

(20)

夹角由两直线的方向向量决定，即

(21)

引入中间变量M、N、P为

(22)

参数变量t1和t2表示为

(23)

由此可知，公垂线与式(20)中2条直线分别相交于垂足A与B，即

(24)

公垂线的长度即垂足A与B之间的距离：

(25)

将式(21)和式(25)代入式(3)，可以得到LIDM单个驱动臂分支的传递功率为

P=|dsinθ|

(26)

从前文分析可知，瞬时传递功率与LIDM的几何构型参数、LSR当前位姿及其对时间的一阶导数相关。由于不同几何构型参数下的LIDM的瞬时传递功率在捕获阶段的值一般都不同，即瞬时传递功率的绝对值没有一个统一的标准来比较和评价LIDM传递性能的优劣。查阅相关文献可知，评价指标一般采用类似于比值的概念进行比较，简单来说，即将当期实际状态下的瞬时传递功率与理论上可能达到的最大传递功率的比值作为评价标准，该比值数值越大，则证明机构本身越接近可能存在的最大传递功率，构型也就越优秀。

2.5 瞬时能效功率比

为了建立LIDM关于传递功率评价指标，引入瞬时能效功率比的概念，表示为

(27)

可以看出，瞬时能效功率比的求解在于如何计算瞬态下构型可能存在的最大传递功率Pmax，由式(3)可得

(28)

由式(28)可知，LIDM最大传递功率的求解问题，等价于寻找运动旋量与力旋量轴线间公垂线可能的最大长度。

单纯从数学角度来看，空间中相对位置关系未知的2个螺旋量，公垂线理论最大长度值显然是无穷大，所以必须回归弱撞击对接机构本身。如图4所示，这里参考文献[9]采用特征点法进行求解，即对于任一构型参数下的LIDM，按照某一统一标准，寻找传递力旋量Si2轴线上的某一点Q，以Q向运动旋量Si1作垂线，以该垂线长度记为可能存在的dmax。鉴于当前LIDM的传递力旋量必定经过各个驱动臂与LSR连接的铰接点ai，选取相应铰接点ai作为特征点Q，以此求解构型下可能存在的最大传递功率Pmax，代入式(27)即可求得瞬时能效功率比。

图4 最大传递功率求解示意

3 算例及结果分析

利用MATLAB编制相应程序，设计基座环结构角β=20°，对接环结构角α=20°，LSR球铰链对应铰点圆半径r=600 mm，基座虎克铰链对应铰点圆半径R=800 mm，初始状态下的LSR距基座的平衡距离H=500 mm。

LIDM在捕获对接过程中的工作空间范围为：定义径向X、Y方向上为-130～130 mm，轴向Z方向参考原初始位置为-300～300 mm。姿态角偏差为5°，在单独考虑工作空间中某一位姿分量下，瞬时传递功率比的变化趋势时，选取其余分量数值为0。

计算6类工况下6根驱动臂的瞬时能效功率比随工作空间的变化情况，如图5～图10所示。

图5 瞬时传递功率比随工作空间X轴分量的变化趋势

图6 瞬时传递功率比随工作空间Y轴分量的变化趋势

图7 瞬时传递功率比随工作空间Z轴分量的变化趋势

图8 瞬时传递功率比随工作空间偏航角分量的变化趋势

图9 瞬时传递功率比随工作空间俯仰角分量的变化趋势

图10 瞬时传递功率比随工作空间滚转角分量的变化趋势

上述6种工况反映了选取其余分量为0，仅独立考虑当前的工作分量变化下，瞬时能效功率比的变化趋势。图像中的部分曲线重合，这正是由于几何构型参数的对称性决定的。从图5～图10可以看出，瞬时能效功率比大多呈现单调性，大多数工况下该构型的LIDM的瞬时能效功率比在0.2～0.5之间，其中对接主方向跨度最大，随着驱动臂执行推杆的推出，功率效能也在逐步升高。

在算例的验证中，发现如果对于某一构型、某一位姿下的LIDM，无论其LSR的速度信息或者受力情况如何，瞬时能效功率比都是确定的。换句话说，瞬时能效功率比仅与LIDM当前几何构型参数及LSR当前位姿相关，而与LSR位姿的一阶导数、受力情况均无关。由此获知，空间中LIDM的构型一旦得以确定，就会得到唯一的瞬时能效功率比，与所受的外界环境信息没有关系，这一结论恰恰说明了瞬时能效功率比可以看作系统的固有属性，体现其作为性能指标的优越性。

4 结束语

本文针对一类空间弱撞击对接机构的传递功率进行了具体的分析，以螺旋理论作为建模手段，通过求解运动螺旋与力螺旋的互易积，来推导空间弱撞击对接机构传递功率的具体表现形式。同时为了建立合理的性能评价指标，提出了瞬时能效功率比的概念，以传递功率比值的形式给出，并结合具体的工况算例呈现其于工作空间中的分布规律。算例验证中发现瞬时能效功率比与LSR位姿的一阶导数、受力情况等外界因素均无关，表现出其作为性能指标的优越性。本文研究内容为后续的空间对接机构结构参数优化等研究提供参考依据。