基于多特征融合的城市轨道交通短时客流预测

李兆丰，倪少权,2,3，孙克洋，吕苗苗,2,3

基于多特征融合的城市轨道交通短时客流预测

李兆丰1，倪少权1,2,3，孙克洋1，吕苗苗1,2,3

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 综合交通运输智能化国家地方联合工程实验室，成都 611756；3. 综合交通大数据应用技术国家工程实验室，成都 611756）

客流需求是城市轨道交通运营组织的基础，随着信息采集技术、计算能力等的快速发展，短时客流推演的准确性在成网条件下尤为关键。考虑到客流的时间依赖性、空间关联性与外部因子随机性影响，以LSTM神经网络为基础预测框架，构建融合多特征的“端到端”短时客流预测框架，挖掘客流的时间依赖性特征，通过Embedding层嵌入外部因子稀疏矩阵，再利用全连接层融合时间特征、空间特征和其他因子得到预测结果。以成都地铁火车南站为实例研究对象，经多次实验，与ARIMA模型与LSTM神经网络相比，融合多特征的组合预测模型预测性能最佳，训练集和验证集MAE误差分别为11.49和10.85，并在测试集上对模型进行测试，结果表明，该模型具有较佳的预测精度和鲁棒性。

城市轨道交通；短时客流预测；多特征融合；端到端预测框架；时空关联性

0 引 言

近年来，随着我国城市轨道交通建设的快速推进，众多城市轨道交通系统已实现网络化运营，客流需求作为组织城市轨道交通线网日常运营的前提与基础，客流预测在成网运营条件下至关重要。客流预测结果过大，会引起人力、物力和财力的极大浪费，客流预测结果过小，则会造成车站、车厢拥挤，轻则引起乘客满意度降低，重则造成人员伤亡等严重后果。因此，选择合适的客流预测方法，提高客流需求预测的准确性尤为关键。

客流属于交通流的一种，而且交通流问题的研究由来已久，并取得了相当丰富的研究成果。如吕田[1]提出了基于SDZ-GRU的多特征短时交通流预测方法SGMTFP，该方法在客流数据基础上加入时间信息等其他因素，通过SDZ改进门控循环单元，构成新RNN单元，动态控制单元间传输，从而进行短时交通流量预测；崔洪涛[2]等提出了深度长短期记忆网络DLSTM方法进行地铁进站客流量预测，采用多源数据构造数据特征；Ding[3]利用客流分解方式将客流序列分解为常数项和误差项两部分，建立ARIMA模型预测常数项部分，利用广义自回归条件异方差模型检测高峰期、大型活动等突发事件情况下客流的波动性；Yang Liu[4]基于深度学习与交通理论，构建基于长短期记忆网络（LSTM）的端到端深度学习架构，实现了外部因素、时间依赖性、空间特征和线网特征的整合与建模；罗向龙[5]等针对交通流的时空性，提出了KNN-LSTM模型，通过-最近邻筛选检测站再将数据输入长短时记忆模型进行预测；陆百川等[6]融合多源数据，并结合GA-WNN模型进行短时交通流预测，该模型克服单源数据的局限性进行全局搜索并且可以具有自适应学习的特点；刘帆洨[7]等考虑票价等其他特征变量为输入属性，构建短时客流预测模型；Zhang[8]基于谱分析技术，构建ARIMA模型与GARCH模型，分别对客流序列的确定性部分和波动性部分进行预测。

总的来说，针对短时交通流预测主要基于线性理论、非线性理论、人工智能、组合预测模型以及交通仿真的预测方法[9-11]。一方面，现有研究大都以历史数据为基础，通过挖掘客流规律的相似性、依赖性以完成预测[9]。然而，在实际情况中，乘客出行具有极大的不确定性，天气状况会对出行是否发生、交通工具选择产生影响，在客流序列特征挖掘方面，大多数研究只考虑客流序列的时间特征，未考虑客流发生的空间位置关联性，同时在预测因子选择上具有主观性。另一方面，在不同输入特征融合方面，当前诸多研究中所建立的组合模型多为不同部分结果的融合，未充分考虑预测框架的整体性和特征融合的合理性[10, 12-14]。

基于此，本文以LSTM神经网络为基础框架，构建融合时间特征、空间特征和外部因子的“端到端”短时客流预测框架。其一，针对时空维度预测因子确定，利用Pearson相关系数法和Spearman相关系数法分别分析客流序列时间相关性和空间关联性，并以此客观确定时间维度和空间维度输入属性；其二，构建以LSTM神经网络为核心，融合时间特征、空间特征和外部因子的“端到端”短时客流组合预测模型，综合考虑不同影响因子对客流的影响，以提高短时客流预测的精度。

1 模型构建

1.1 基于相关系数法的时空预测因子选择

当前轨道交通短时客流预测研究大都集中于预测方法选择和改进，忽略了输入属性对预测模型性能影响，预测因子选择具有主观性，在模型预测过程中引入了大量噪声点，降低了模型预测效率。在客流预测中，输入属性的好坏直接影响预测精度，一方面，若考虑的输入属性过少或者输入属性选择不合适，则直接导致结果精度较低；另一方面，输入属性过多，考虑的影响因素中包含影响因子较小的属性，会使得预测模型更加庞大，造成模型的计算复杂度指数级增长，浪费计算资源和造成无法求解的问题。因此，针对输入属性选择问题，本文提出利用相关系数法确定时间与空间维度的预测因子。

相关研究表明[15]，在城市轨道交通线网中，不同站点的客流量之间存在潜在的关联性，同时，客流序列是时间序列的一种，具有时间序列的依赖性等特征。历史客流数据是在特定时间和空间条件下，综合交通发生、吸引与线网服务水平等长期影响因素以及天气状况等随机影响因素下实际进站客流量统计值，蕴含了客流波动规律、不同影响因素对客流的影响程度大小等客流波动特征。历史某一时段客流量，代表了其在所有影响因素综合作用条件下，某一站点或线路在该时段的实际客流量值。因此，本文选取Pearson相关系数法与Spearman等级相关系数法分别分析时间依赖性与空间关联性大小，并以此为依据确定时间维度与空间维度的输入属性。

1.1.1 Pearson相关系数法基本原理

Pearson相关系数法是检验变量之间相似性程度的一种有效方法，计算公式如下：

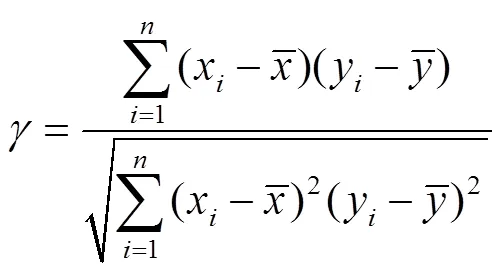
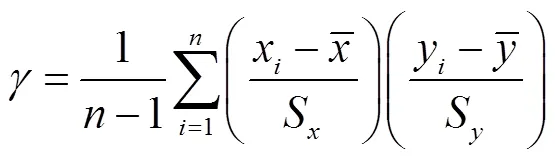
1.1.2 Spearman等级相关系数法基本原理

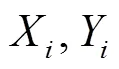
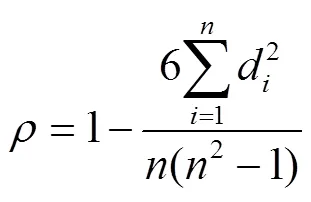
1.2 多特征融合的组合预测模型构建

针对客流序列的非线性和波动性特征，单一的预测方法都存在一定的缺陷，同时，对于多特征融合问题，当前组合预测模型是对不同部分结果的融合，缺乏客观性和合理性。本文模型构建的目标是挖掘不同维度的特征并融合，实现该目标需要解决以下几个关键问题：第一，如何挖掘客流序列的时间依赖性；第二，如何解决外部因子矩阵的稀疏性；第三，如何客观地融合时间特征、空间特征和外部因子。

因此，对于上述关键问题，构建以LSTM神经网络为核心，融合时间特征、空间特征和外部因子的“端到端”短时客流组合预测模型。基本思想是利用LSTM神经网络挖掘和学习预测站点及与预测站点相关性较大的8个站点客流序列时间依赖性特征，通过Embedding层嵌入外部因子稀疏矩阵并利用“+”操作融合这两步结果作为全连接层输入，经全连接层非线性映射输出预测客流时间序列。

1.2.1 基于LSTM神经网络的时间依赖性挖掘

LSTM神经网络（长短期记忆循环神经网络）是一种改进的循环神经网络，能够有效地解决时间序列的长期依赖问题。它是在RNN神经网络的基础上引入时序的概念，对于LSTM单元，上一LSTM单元的隐节点输出与本LSTM单元的输入共同作为当前LSTM单元的输入，通过门控决定细胞状态的记忆与遗忘，同时有效解决时间序列的长期记忆问题和梯度消失与爆炸问题[16,17]。

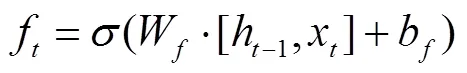
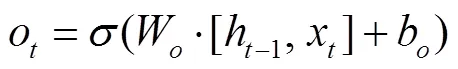
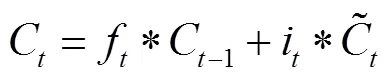
图1 LSTM单元内部结构

LSTM单元中门控结构控制信息的“遗忘”与记忆并调整隐藏状态h，基于此，LSTM神经网络具有强大的信息“记忆”功能，可以有效地挖掘客流序列的时间依赖性。

图2所示是不同站点基于时间依赖性挖掘的初步预测框架，其中表示个站点，表示前步预测输入，表示预测后步客流。

1.2.2 基于Embedding层的外部因素嵌入

Word Embedding是一种基于神经网络的语言模型，以获取词的分布式表达方式，自动从文本语料中学习词的低纬度、稠密和实数向量的表达形式，在经Word Embedding处理之后，稀疏矩阵的稀疏性可大幅降低，且分布具有一定的规律性，其目的是将输入的高维度映射到低纬度的表示。

对于天气等外部因子，本文利用类别标签标定天气类别，并利用One-hot编码表示类别特征，具有较大的稀疏性，因此，本文采用Embedding方法将稀疏矩阵进行嵌入。

小儿腹泻是儿科高发疾病,如果不及时的进行治疗,就会导致患儿的病情迁延,引起营养不良症状,无法正常生长发育[4]。腹泻对小儿的危害性非常大 [5]。小儿患者的消化系统功能不完善,肠道内受到各种病菌的侵害引起了患儿的发病,导致肠道内菌群失调引起腹泻。该疾病影响了水和食物的消化吸收,肠液渗透压上升,导致了渗透性腹泻;产毒性细菌感染会对肠粘膜溶质运转造成影响,导致分泌性腹泻。不同原因引起的腹泻,其生理变化特征存在差异性,小儿腹泻疾病都有一个共通之处,肠道内环境被破坏,菌群失调。

图2 多站点“多对多”LSTM神经网络预测框架

1.2.3 基于全连接层的多特征融合

式中，为sigmoid激活函数；为第i个神经元输入；O为输出预测值；为输入层第i神经元与隐藏层第j神经元的权重值；为隐藏层第j神经元与输出层的权重值。

1.2.4 多特征融合的短时客流预测模型

图4所示是预测模型整体框架，在预测模型训练时，每一轮迭代计算真实值与预测值误差，通过误差反向传播迭代更新模型内部参数，实现从样本数据中自适应学习和调整模型参数，使得不同特征融合更合理、客观。预测整体框架由LSTM模块、Embedding模块和全连接层融合模块三部分构成。

（1）LSTM模块：将空间相关性较高的站点前时段客流输入到LSTM神经网络，挖掘客流序列的时间依赖性特征并输出初步预测结果。

（2）Embedding模块：首先通过One-hot编码对天气和客流模式特征进行编码形成稀疏矩阵，利用Embedding层将稀疏矩阵映射为与LSTM输出具有一致维度的向量。

（3）全连接层融合模块：利用“+”操作将外部因素和初步结果融合得到全连接层的输入，利用全连接层挖掘和融合不同特征输出预测客流时间序列。它为典型的三层全连接神经网络结构，共有三层，分别为输入层、隐藏层和输出层。

图4 预测模型整体框架

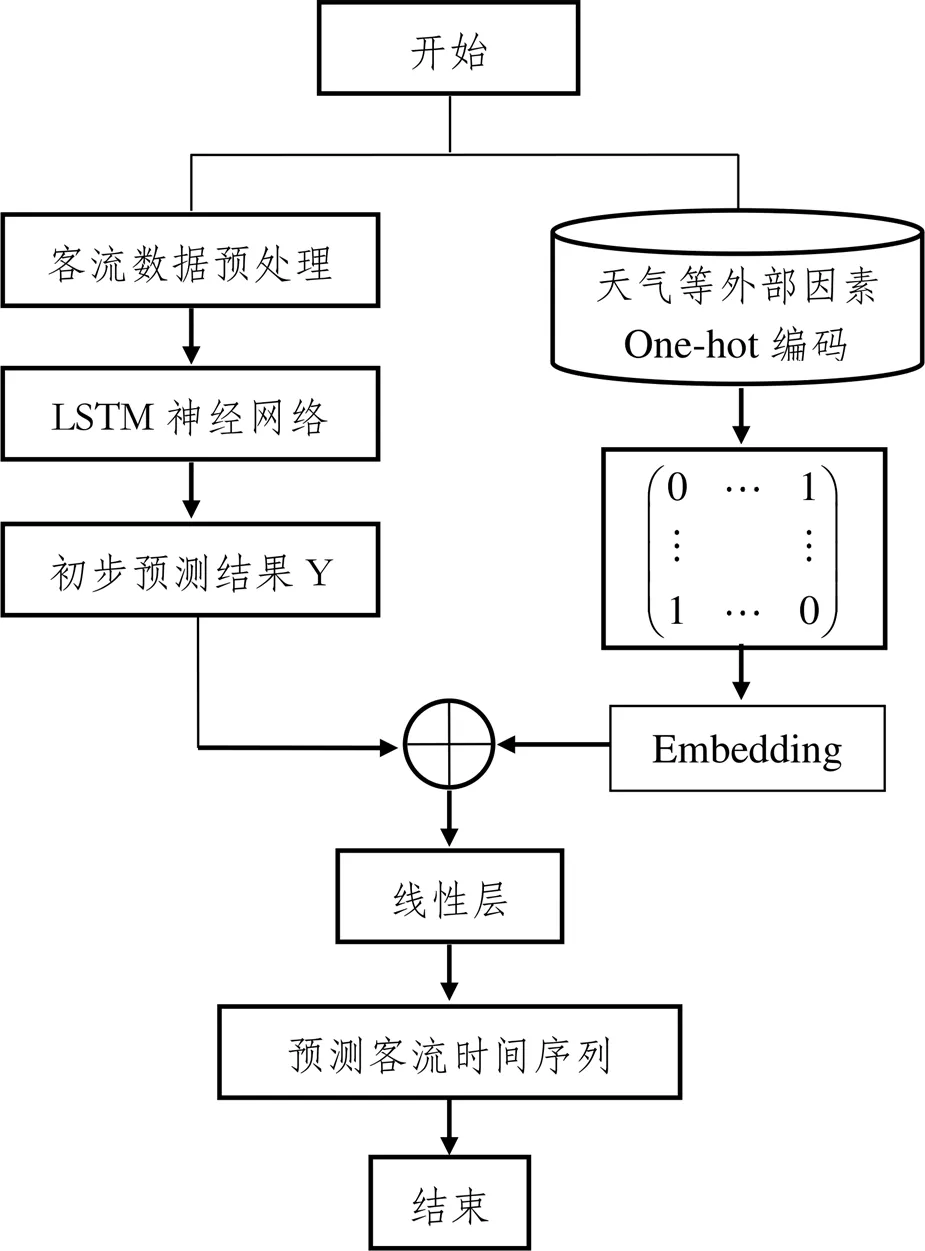
图5 具体预测步骤流程图

（1）客流数据预处理：对不同站点客流进行采样，生成客流时间序列。

（2）LSTM神经网络预测：对于具有较强空间关联性的站点，利用LSTM神经网络挖掘各站点的时间依赖性特征，并输出各站点的初步预测结果。

（3）Emebedding层嵌入外部因子矩阵：针对天气特征和日期特征的稀疏矩阵，利用Embedding层降维嵌入与初步预测结果相同维度的向量。

（4）外部因子与初步预测结果融合：对嵌入后的外部因子向量与初步预测结果向量进行“+”操作得到中间结果。

（5）全连接层特征融合：将（3）中中间结果作为全连接层输入，输出则为预测客流时间序列。

2 实例分析

2.1 数据来源

本实例选取成都地铁2017年11月共30天数据，选取15min粒度下每日有效时段为6:00~ 23:30，共计68个时段。

在神经网络训练之初，首先需要构造样本数据集并将数据集划分为训练集、验证集和测试集。一般来说，数据集划分比例为8∶1∶1或者6∶2∶2，考虑到本实例数据只有一个月共30天数据，样本量少，因此，选取2017年11月23日（周四）和2017年11月26日（周日）为验证集，选取2017年11月30日（周四）为测试集样本，其余样本为训练集数据。

2.2 性能评价指标

在科学研究过程中，通常采用误差来评价预测方法的性能和预测结果的有效性。本文采用平均绝对误差作为预测性能评价指标[13，18]。

平均绝对误差（MAE）表示所有单个预测值与真实值的偏差绝对值的平均，能够较好地反映误差的实际情况，计算公式为：

均方误差（MSE）能够反映误差分布的集中程度，其值越小表示误差分布越集中，计算公式为：

2.3 实例结果分析

本文计算当前时段客流与前时间段客流的Pearson相关系数大小，抽取前5时段的相关系数如表1所示，计算火车南站与全网所有站点客流Spearman等级相关系数值，并抽取关联性较大的8个站点如表2所示。依据相关性分析结果，确定前四时段客流量为时间维度的输入因子，确定与预测站点Spearman相关系数最大的8个站点作为空间维度的输入预测因子。

根据天气状况和全日最高温度将天气划分为7类（晴/多云/阴，≤25度；晴/多云/阴，>25度；晴/多云/阴和小雨，≤25度；晴/多云/阴和小雨，>25度；小雨/小雨，≤25度；小雨/小雨，>25度；阴/小雨和中雨）。

表1 不同时段客流量之间的Pearson相关系数表

Tab.1 Pearson coefficients of passenger flow at different time intervals

表2 火车南站Spearman相关系数表

Tab.2 Spearman coefficients for the South railway station

客流分析结果表明，站点客流在工作日与非工作日具有较大的差别。在工作日，居民出行目的大都为工作、上学等，根据站点所处空间位置差异，一般具有明显的早晚高峰特征；而在非工作日，居民出行目的大都为购物、访友等，早晚高峰特征并不明显，且工作日之间客流波动情况高度相似，周六周日之间客流波动情况较为相似，因次，本文将周内客流划分为工作日与休息日模式两类。

一般来说，利用虚拟变量对定性指标进行类别特征划分，但由于日期特征及天气特征中的不同类别，故不存在严格的大小关系，采用0，1，2，…这种量化方式显然不太合适。在机器学习中，对于类别标签这种标称特征，采用独热编码技术创建一个新的虚拟特征，具体编码结果见表3。

表3 定性指标量化结果

Tab.3 Quantitative results of qualitative indicators

在神经网络训练过程中，为提高模型预测性能及泛化性能，采用了学习率衰减、Xavier初始化、权值衰减策略、随机超参数调试策略与SGD优化器。在神经网络训练之初，需指定超参数取值或者取值范围，本文所选取超参数搜索空间如表4所示。

表4 超参数取值或取值空间

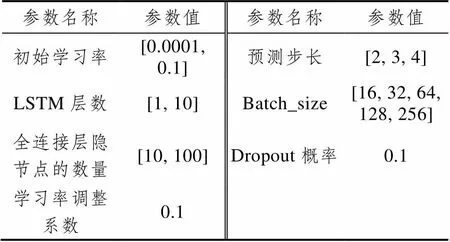
Tab.4 Value intervals of hyper-parameters

经多次实验和调试之后，当初始学习率取0.01、预测步长为2、LSTM层数为2、Batch_size为128、全连接层隐节点数量为96，Dropout概率为0.2时，训练集和验证集误差最小，MAE误差和MSE误差曲线如图6和图7所示。其中训练集MAE和MSE误差分别为11.49和0.00084，验证集MAE和MSE误差分别为0.00079和10.85。由图6可看出，预测模型前期迭代过程中震荡性较大，在迭代50次左右时，误差曲线逐渐趋于平缓，而且震荡性较小，在迭代350次左右时，趋于平缓。如图7所示，MSE误差在前50次震荡程度较大，迭代50次之后其变化程度较小，这是由于MSE误差是在标准化数据下计算的误差，便于模型迭代求优，MAE误差是在反归一化之后计算的误差。

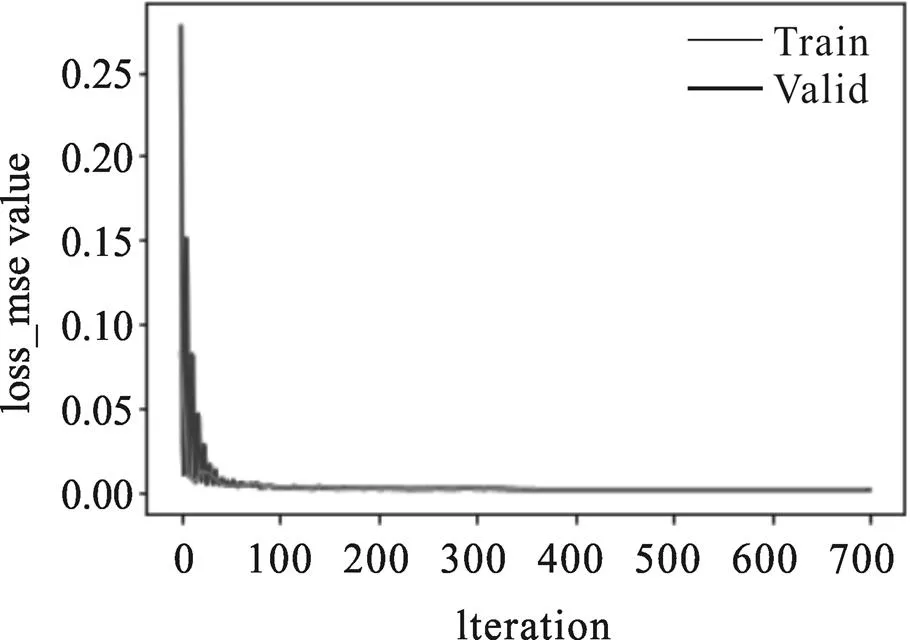
图6 训练集MSE误差

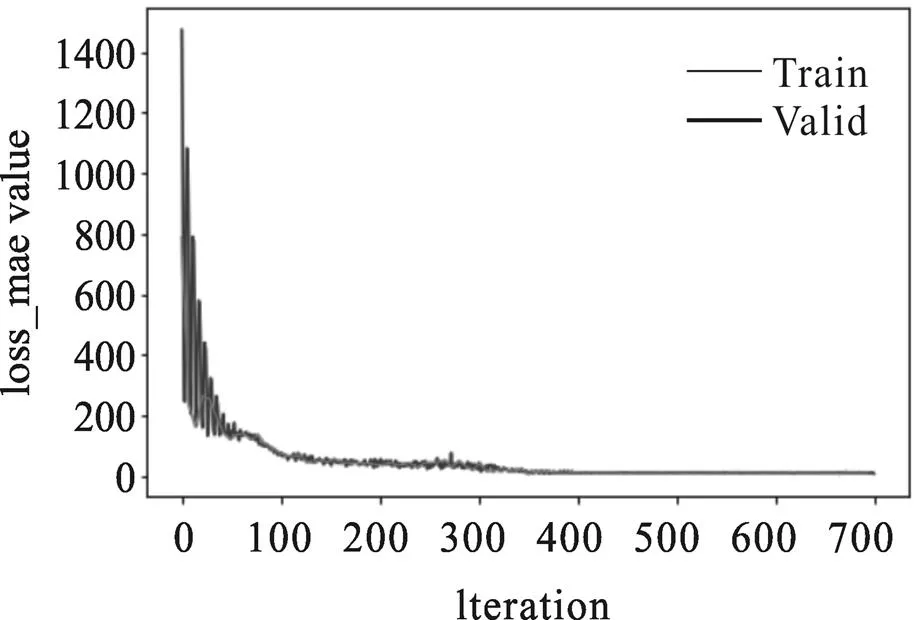
图7 验证集MAE误差

为验证本预测模型的有效性，本文选取传统ARIMA模型和单一LSTM神经网络为对比参照模型，经多次试验与调试，得到三个模型在训练集和验证集的性能表现如表5所示。本文所提模型在训练集和验证集上的MAE误差和MSE误差分别为11.49和10.85，远小于ARIMA和单一LSTM，其预测性能较ARIMA和LSTM更佳。

表5 模型的性能表现

Tab.5 Performances of different models

利用训练好的模型，对测试集进行预测，其中2017.11.30预测值与真实值对比如图8所示，实线Real是真实值，实线Pred是多特征融合的组合预测模型预测值，实线LSTM_pred指单一LSTM神经网络预测值，实线ARIMA_pred指ARIMA模型预测值。由图8可看出，多特征融合的组合预测模型能够较好地拟合客流变化特征，对高峰期客流突变有较好的识别性和拟合性，总体来说，模型预测性能表现稳定且精度较佳；单一LSTM神经网络可以大致拟合客流变化趋势，但对于客流突变点、高峰点不能很好地识别和预测，因此不能适应波动性较大的客流序列预测；针对ARIMA模型，可以识别客流的早晚高峰，挖掘大体的客流变化趋势特征，但是无法拟合客流波动性大的特征。

图8 2017.11.30预测值与真实值对比图

由表5与图8可知，LSTM神经网络在客流序列的时间依赖性发掘方面较ARIMA模型更佳，本文所提出的基于多特征融合的“端到端”短时客流预测模型性能最佳，这表明考虑时间维度、空间维度和外部因子作为预测输入属性，能够有效提高模型预测性能和精度，同时，“端到端”的预测框架能够自适应发掘特征融合的客观规律。

3 结束语

本文考虑客流序列的时间依赖性、空间关联性和外部因子建立多特征融合的“端到端”预测框架，利用全连接层融合不同特征，综合考虑客流的不同影响因子。基于梯度下降法从真实数据中自适应学习不同特征的方式，引进学习率衰减、Xavier初始化、权值衰减策略和Dropout策略以提高模型预测性能。选取ARIMA模型和LSTM神经网络进行对比实验，结果表明，基于多特征融合的组合预测模型具有更佳的预测精度，其在训练集、验证集和测试集上的MAE误差分别为11.49、10.85和11.98。综上，融合多特征的“端到端”预测框架在客流预测上有更好的成效。但本文只预测单一站点的客流量，未实现全网客流同步预测，未来还需进一步研究全网客流整体预测。

[1] 吕田. 基于SDZ-GRU的多特征短时交通流预测方法[J]. 计算机与现代化, 2019 (10): 60-65.

[2] 崔洪涛, 陈晓旭, 杨超, 等. 基于深度长短期记忆网络的地铁进站客流预测[J]. 城市轨道交通研究, 2019, 22 (9): 41-45.

[3] DING C, DUAN J, ZHANG Y, et al. Using an ARIMA-GARCH modeling approach to improve subway short-term ridership forecasting accounting for dynamic volatility [J]. IEEE Transactions on Intelligent Transportation Systems, 2017, pp (99): 1-11.

[4] LIU Yang, LIU Zhiyuan, JIA Ruo. DeepPF: a deep learning based architecture for metro passenger flow prediction[J]. Transportation Research Part C, 2019 (101):18-34.

[5] 罗向龙, 李丹阳, 杨彧, 等. 基于KNN-LSTM的短时交通流预测[J]. 北京工业大学学报, 2018, 44 (12): 1521-1527.

[6] 陆百川, 舒芹, 马广露. 基于多源交通数据融合的短时交通流预测[J]. 重庆交通大学学报: 自然科学版, 2019, 38 (5): 13-19, 56.

[7] 刘帆洨, 彭其渊. 铁路旅客购票需求预测模型研究[J]. 交通运输工程与信息学报, 2018, 16 (2): 50-56.

[8] ZHANG Y, ZHANG Y, HAGHANI A. A hybrid short-term traffic flow forecasting method based on spectral analysis and statistical volatility model [J]. Transportation Research Part C-emerging Technologies, 2014, 43: 65-78.

[9] LEE S, FAINBRO D. Application of subsct autoregressive integrated moving average model for short-term freeway traffic volume forecasting [J]. Journal of the Transportation Research Board. 1999: 179-188

[10] CHENMuchen, YU Wei. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks[J]. Transportation research, Part C. Emerging Technologies, 2012, 148-162

[11] 马小磊, 丁川, 于海洋, 等. 公共交通大数据挖掘与分析[M]. 北京: 人民交通出版社, 2017.

[12] WEI Y, CHEN M. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks [J]. Transportation Research Part C: Emerging Technologies, 2012, 21 (1): 148-62.

[13] 胡进宝. 基于双层分解和核函数极限学习机的城市轨道交通短时客流预测[D]. 北京：北京交通大学, 2017.

[14] ZHANG Y, ZHANG Y, HAGHANI A. A hybrid short-term traffic flow forecasting method based on spectral analysis and statistical volatility model [J]. Transportation Research Part C: Emerging Technologies, 2014,(43) 65-78.

[15] 黄梓荣. 轨道交通线网客流预测方法研究[D]. 广州：华南理工大学, 2015.

[16] 张琳. 基于深度神经网络的地铁客流预测系统研究[D]. 北京：北京交通大学, 2019.

[17] 张伟林. 基于深度学习的地铁短时客流预测方法研究[D]. 深圳：中国科学院大学深圳先进技术研究院, 2019.

[18] 周志华. 机器学习[M]. 北京：清华大学出版社, 2016.

Short-term Passenger Flow Prediction of an Urban Rail Transit Based on Multi-feature Fusion

LI Zhao-feng1, NI Shao-quan1,2,3, SUN Ke-yang1, LV Miao-miao1,2,3

(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu 611756, China;3. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Chengdu 611756, China)

Passenger flow demand is a major prerequisite for the operations of an urban rail transit. With the rapid development of information collection technology and computing capabilities, the accuracy of short-term passenger flow deduction is especially critical when networks are established. Considering time dependence, the spatial correlation of passenger flow, and the randomness of external factors, an “end-to-end” short-term passenger flow prediction framework that incorporates multiple features is constructed based on a long short-term memory (LSTM) neural network. The LSTM neural network is used to mine the time-dependent characteristics of passenger flow. In addition, an external factor sparse matrix is embedded in the embedding layer, and a fully connected layer is used to fuse temporal features, spatial features, and other factors to obtain prediction results. Chengdu Metro South Railway Station was used as a case study. Following several experiments and based on a comparison of the autoregressive integrated moving average (ARIMA) model and LSTM neural network, the combined prediction model incorporating multiple features showed the best prediction performance, where the mean average errors of the training and validation sets were 11.49 and 10.85, respectively. In addition, the combined prediction model was tested on a test set and results showed that the model had better prediction accuracy and robustness than the ARIMA model and LSTM neural network.

urban rail transit; short-term passenger flow prediction; multi-feature fusion; end-to-end prediction framework; spatio-temporal correlation

1672-4747（2020）04-0093-10

U293

A

10.3969/j.issn.1672-4747.2020.04.012

2020-03-12

国家重点研发计划资助（2017YFB1200702）；国家自然基金项目（61703351，71971182）；中国铁路总公司科技研究计划项目（P2018T001，P2018X001，N2018X006-01）; 四川省科技计划项目（2020YFH0035，2020YJ0268，2020YJ025，2020JDRC0032）

李兆丰（1994—），男，湖南岳阳人，西南交通大学硕士研究生，研究方向：短时客流预测方法，E-mail：leezhaofeng94@foxmail.com

吕苗苗（1986—），女，山西文水人，西南交通大学讲师，研究方向：铁路运输组织与优化，E-mail：314809108@ qq.com

李兆丰，倪少权，孙克洋，等. 基于多特征融合的城市轨道交通短时客流预测[J]. 交通运输工程与信息学报，2020, 18(4):93-102

（责任编辑：刘娉婷）