悬挂系统参数对高速列车横风运行安全性的影响
2020-12-24周鹏,常城,李田,秦登
周 鹏,常 城,李 田,秦 登
悬挂系统参数对高速列车横风运行安全性的影响
周 鹏1,常 城2,李 田2,秦 登2
(1. 西南交通大学,交通运输与物流学院,成都 611756;2. 西南交通大学,牵引动力国家重点实验室,成都 610036)
列车悬挂系统参数的变化会对其运行安全稳定性产生影响,特别是在横风等复杂运行环境下。针对国内某型号动车组,数值仿真了横风下的列车气动特性,并研究了悬挂系统参数相对标准值变化对运行安全稳定性的影响。研究结果表明:横风作用下,头车一位轮对脱轨系数随二系空气弹簧垂向刚度、二系空气弹簧横向刚度、一系钢弹簧垂向刚度、一系钢弹簧横向刚度的增加而减少;轮轴横向力会随着二系空气弹簧垂向刚度、一系钢弹簧垂向刚度、一系钢弹簧横向刚度的增加而减少,随着一系钢弹簧纵向刚度的增加而增加;轮重减载率随着二系空气弹簧垂向刚度、二系空气弹簧横向刚度、一系钢弹簧纵向刚度、二系横向减振器阻尼的增加而减少;轮轨垂向力会随着二系空气弹簧横向刚度、一系钢弹簧纵向刚度、二系横向减振器阻尼的增加而减少,随着一系钢弹簧横向刚度、一系钢弹簧垂向刚度的增加而增加。
悬挂系统;车辆系统动力学;横风安全性;高速列车
0 引 言
高速列车运行过程中的第一要求是安全性。从高速列车的出现到今天,列车运行安全性以及舒适性始终是国内外学者研究的热点之一,其影响因素可分为两部分:一是高速列车的运行环境,如横风、路堤以及桥梁等,二是列车整体结构设计以及悬挂系统参数选择。
为了研究高速列车横风环境下的气动特性,国内外学者做了大量的研究。Suzuki[1]分析典型车型在路堤、桥梁上运行时的气动特性,指出高速列车在运行过程中受到的气动力与气动力矩与列车形状以及轨道基础形式有关;Diedrichs[2]等对ICE2在复线路堤上以250km/h车速运行的流场结构进行了详细的分析;Cooper[3]利用风洞实验对列车在横风下的气动特性进行分析发现横风会使列车运行安全性恶化12%;针对高速列车在侧风环境下通过曲线受到的气动载荷,Thomas[4-5]总结了不同阵风载荷对列车气动性能的影响;Kim[6]等提出了一种针对高速列车在横风环境下运行时脱轨系数的计算公式,计算结果与数值模拟结果较为吻合;李振等[7]研究了横风环境下复线路堤上列车周围的流场特性研究表明相较于平地,路堤上列车周围的气流流速更大,导致路堤上列车气动性能较平地上恶劣;龙苏琴等[8]研究了横风环境中不同路堤高度及倾角下列车气动性能的差异,研究表明路堤高度以及倾角越大,列车的横向力和侧滚力矩就越大;任尊松[9]计算了作用在列车上的气动载荷,在此基础上计算了横风对列车运行安全性的影响。
此外,列车悬挂系统参数对列车动力学性能的影响研究也较为成熟。王开云等[10]计算分析了不同悬挂参数下“天梭”号电力机车的气动性能;程冰[11]对CW-200W型转向架进行了结构设计的改进以及悬挂参数的优化研究;池茂儒等[12]通过分析高速客车转向架悬挂系统参数,提出适当的减少二系悬挂的横向刚度,能够有效的提升车辆运行的横向平稳性;崔涛等[13]针对国内部分高速列车车辆晃动问题,通过分析得到最优的参数方案;董锡明[14]指出高速列车的行车安全性和乘坐舒适度与转向架的取值是否合理密切相关;刘宏友[15]研究总结增加各车之间的横向连接阻尼系数将有利于提高列车的曲线通过性;陈华斌等[16]等研究了悬挂刚度和悬挂阻尼对蛇行临界速度的影响,分析了悬挂刚度和阻尼对运行平稳性的影响。
以上研究只是针对列车在横风环境下运行安全性,或是悬挂参数变化对列车运行安全性的影响,缺乏高速列车在横风环境下运行时悬挂系统参数变化对列车运行安全性影响研究,本文以此为出发点,以国内某型号动车组为研究对象,考虑列车运行速度为250km/h和横风速度为20m/s,研究悬挂系统参数变化对横风下列车运行安全性的影响。
1 列车空气动力学模型及计算结果
计算模型取国内某三车编组列车模型,其空气动力学计算区域和边界条件如图1所示,其中计算域长度、宽度和高度分别为400m、100m和40m。其中正前方的速度入口距头车鼻尖点100m,列车正后方的压力出口距尾车鼻尖点200m,列车车体底面距离地面0.376m,列车位于计算区域中心截面上。头尾车车身最大网格尺寸为60mm,转向架最大网格尺寸为25mm,网格数量约为3583万,表面网格示意如图2所示。

图1 计算域与边界条件示意图

图2 头车及转向架的表面网格
列车运行正前方及右侧面为速度入口边界,速度为列车运行速度和环境风的合成风速,运行正后方及左侧面为压力出口边界,地面设置为滑移壁面以模拟地面效应,滑移速度为列车运行速度,顶面为对称边界。采用流体计算软件STAR-CCM+对上述网格进行计算,计算参数设置如下:采用三维、定常、不可压缩两方程SST-湍流模型,输出稳定后求平均值,如表1所示。
表1 列车气动特性

Tab.1 Train aerodynamic characteristics
2 高速列车多体系统动力学模型
为了分析列车在气动作用下悬挂参数变化对其在平地上行驶的安全稳定性影响,采用多体动力学软件SIMPACK建立高速列车动力学模型,如图3所示。车辆系统动力学单车模型由一个车体、两个转向架、四个轮对以及八个转臂组成。刚性车体、构架和轮对均有6个自由度,即纵向、垂向、横向、点头、摇头,侧滚。转臂有1个自由度,即点头。单车模型共计50个自由度,整车模型一共150个自由度[17]。
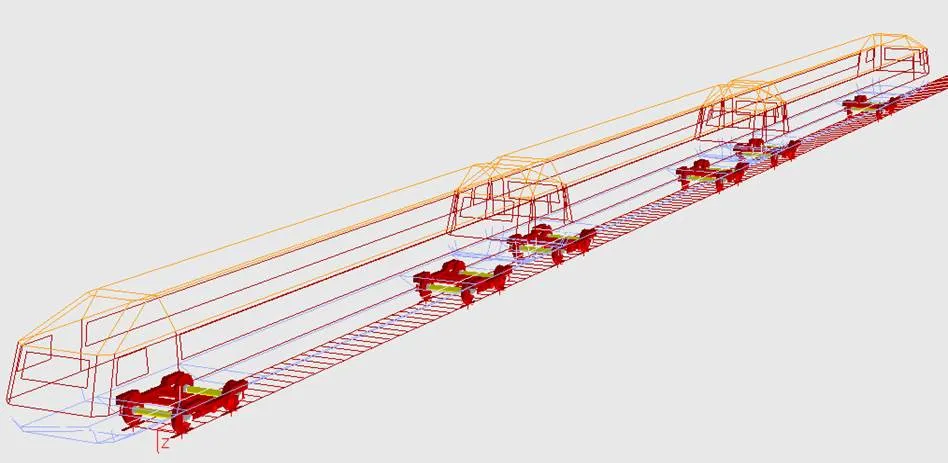
图3 车辆系统动力学模型
车辆系统动力学模型中悬挂系统包括二系空气弹簧、抗蛇形减振器、一系钢弹簧等,车轮踏面类型选择LMA。具体计算工况以国内某动车组列车标准悬挂参数为基准,分别计算悬挂参数为标准值的50%、75%、125%、150%时对列车运行安全性和舒适性的影响,如表2所示。

表2 悬挂参数标准值
3 悬挂参数对列车运行安全性的影响
横风环境中,高速列车还会受到一个较大的侧力作用,对列车运行安全性产生威胁,严重时甚至可能会出现脱轨或者倾覆的情况。以《高速列车整车试验规范》[18]为参考标准,通过分析脱轨系数、轮轨垂向力、轮重减载率和轮轴横向力来评定高速列车的运行安全性。
3.1 脱轨系数与轮轴横向力对列车运行安全性的影响
列车在车辆结构参数、运行和线路状态等不利因素下运行时,可能导致车轮脱轨,某一时刻作用在车轮上的横向力和垂向力的比值/为这一时刻车轮的脱轨系数,该定义最初由法国科学家Nadal提出。
悬挂参数同样对列车横风环境中运行的安全性有很大影响。由图4可知,在气动作用下,头车的一位轮对的脱轨系数受悬挂参数影响较大,特别是二系空气弹簧垂向刚度,其次是二系空气弹簧横向刚度。头车一位轮对脱轨系数随二系空气弹簧垂向刚度、二系空气弹簧横向刚度、一系钢弹簧垂向刚度、一系钢弹簧横向刚度的增加而减少,其中二系空气弹簧垂向刚度减少一半时,脱轨系数的最大值达到1.38,大于安全阈值0.8,使列车有脱轨的风险。

图4 悬挂系统参数变化对列车头车一位轮对脱轨系数的影响
过大的轮轴横向力会导致轮对横移,同时会使线路部件损耗加快甚至损坏导致列车脱轨,《高速动车组整车试验规范》规定高速列车的轮轴横向力允许限值采用计算公式如下:

轮轴横向力增加会使列车运行安全稳定性下降,在横风等复杂线路工况下轮轴横向力增加造成的影响更加恶劣,因此有必要研究高速列车在横风环境中运行时悬挂参数变化对轮轴横向力的影响。研究表明:轮轴横向力会随着二系空气弹簧垂向刚度、一系钢弹簧垂向刚度、一系钢弹簧横向刚度的增加而减少,随着一系钢弹簧纵向刚度的增加而增加,如图5所示。
悬挂装置使列车具有良好的减振特性,缓和车辆与线路之间的相互作用力,减少振动与冲击,从而提高列车在运行过程中的平稳性、安全性和可靠性。列车悬挂参数的变化必然会导致车辆横向或垂向约束发生变化,从而影响列车的运行安全稳定性。

图5 悬挂系统参数对轮轴横向力的影响
以二系空气弹簧垂向刚度变化为例,图6为头车一位背风侧轮对脱轨系数时程曲线。脱轨系数的大小与轮对同时刻轮轨横向力以及轮轨垂向力相关,其中左右两侧轮轨的横向力共同决定了轮轨横向力的值,当二系空气弹簧垂向刚度变化时,列车一位轮对背风侧车轮的轮轨横向力与轮轨垂向力曲线如图7所示。图(a)为轮轨横向力变化曲线,变化趋势与背风侧车轮脱轨系数变化趋势基本相同,随着空簧垂向刚度的相对增加,车轮的最大轮轨横向力随之增加。由图6可知当高速列车在横风环境下运行4s左右时,也就是横风加载量达到最大时,脱轨系数达到最大值,随后急剧减少趋于稳定。脱轨系数为同时刻车轮轮轨横向力与轮轨垂向力的比值,4s之前背风侧轮轨横向力达到最大值,而轮轨垂向力在相同时刻也随时间增加,轮轨横向力和垂向力同时增加,车轮脱轨系数达到峰值。在这个时间周期内,空簧垂向刚度值为标准值的50%时,轮轨横向力变化率为45.7%,轮轨垂向力变化率为13.6%,相对来说,轮轴横向力的增加是背风侧车轮脱轨系数增加的主要原因。
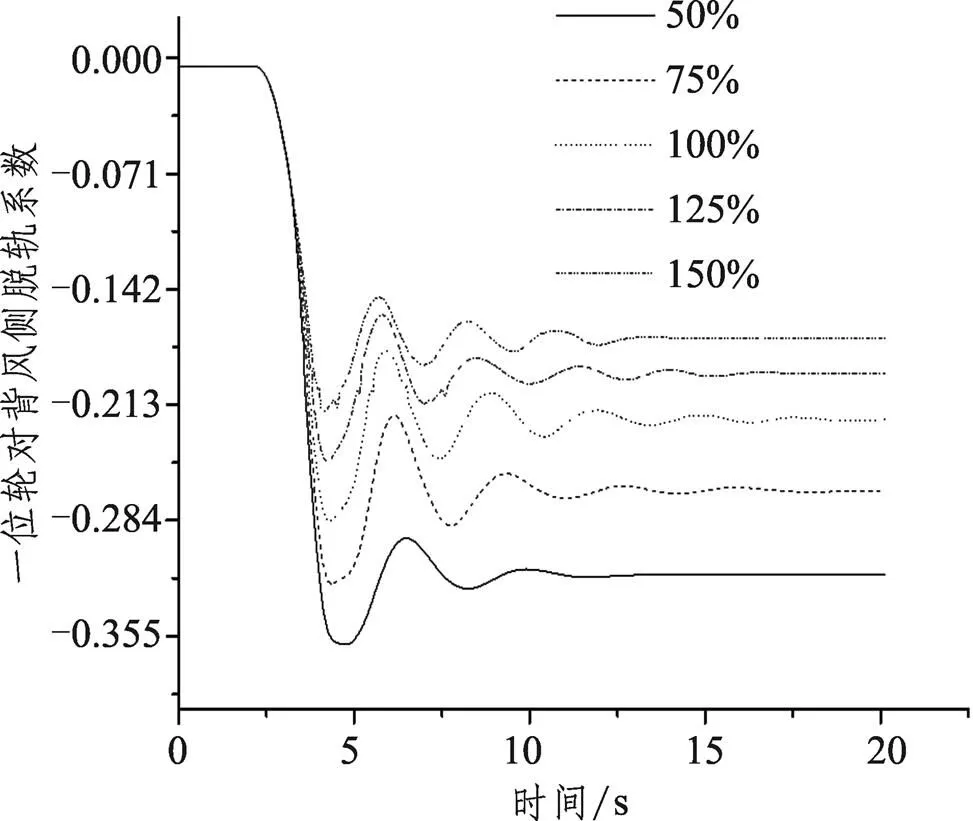
图6 头车一位背风侧轮对脱轨系数时程曲线
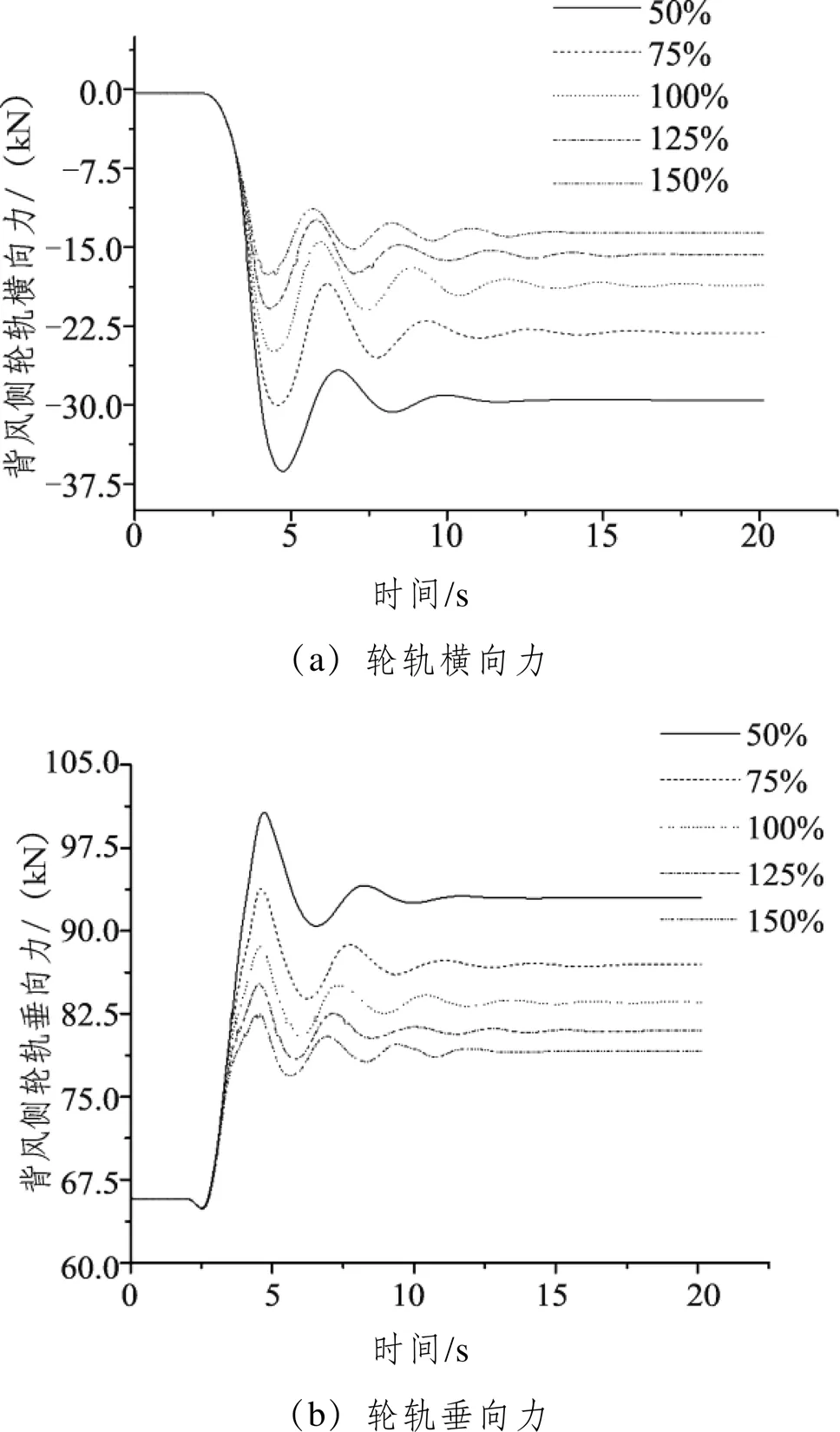
图7 二系空气弹簧垂向刚度对轮轨力的影响
轮对横移是轮轨横向力变化的影响因素之一,同时也是轮轴横向力变化的影响因素。二系空气弹簧垂向刚度变化下头车一位轮对背风侧车轮、转向架1、转向架2和车体的横移量如图8所示。从图中可以看出,在对车体施加气动载荷后,车轮、转向架和车体的横移量发生明显的变化,在气动载荷的作用下,横移量随着列车运行时间的增加急速变化,在4s前后达到最值,之后逐渐变化并趋于稳定。
中央悬挂系统不但能够支撑车体,均匀传递载荷给各个轮轴,同时可以衰减车辆振动和冲击。作为中央悬挂装置组成之一的二系空气弹簧,其垂向刚度变为标准值的50%时,会导致列车的内部约束力度发生变化,使车体向背风侧的横移量发生变化,由标准值的4.84mm减少到3.84mm。转向架承受车体与轮对之间的各种载荷和作用力并使其均匀分配,保证列车平稳运行。当二系空气弹簧垂向刚度发生变化时,转向架抑制车体横向移动的能力发生变化,头车的第一个转向架向迎风侧的横移量增大,由0.98mm增加到1.11mm,第二个转向架的横移量由0.74mm减少到0.70mm,横向作用传递到轮对使轮对横向移动由0.90mm增加大0.93mm。二系空簧垂向刚度减少一半时,车体横移量变化率为20.7%,转向架变化率分别为12.7%和4.3%,车轮横移量变化率为3.1%。由于中央悬挂装置和轴箱悬挂装置的缓冲、衰减和传递等功能,变化率逐渐减少。

3.2 轮轨垂向力与轮重减载率对列车运行安全性的影响
列车运行速度越高,轮轨之间的作用力也越大,轮轨之间的垂向力也会越大,过大的轮轨垂向力会导致轮轨之间的磨损增加,同时过大的轮轨垂向力也会使其他部件如扣件、轨枕产生损伤,定期维护的成本增加,严重时甚至危及行车安全。参考《高速列车整车试验规范》知轮轨垂向力的限制条件为:

根据赫兹非线性弹性接触理论,轮轨垂向力的表达式为:
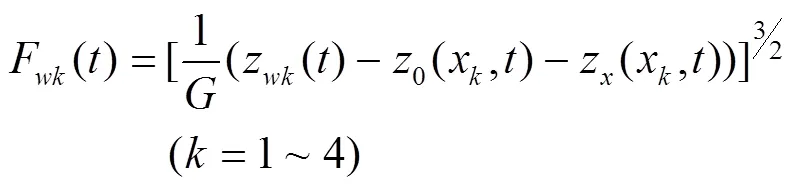
图9(a)为悬挂参数变化对头车最大轮轨垂向力的影响,由图可以看出:轮轨垂向力会随着二系空气弹簧横向刚度、一系钢弹簧纵向刚度、二系横向减振器阻尼的增加而减少;随着一系钢弹簧横向刚度、一系钢弹簧垂向刚度的增加而增加。轮轨垂向力均在规定安全范围之内,这是因为列车空载没有任何负重。
轮重减载率为评定车辆在轮对横向力为零或接近于零的条件下,由于车轮某侧严重减载而脱轨的安全性指标。设

高速列车轮重减载率与车辆的结构参数以及运行工况有关,当高速列车运行过程中悬挂参数变化时,必然导致列车的轮重减载率发生变化。图9(b)为悬挂参数变化对头车最大轮重减载率的影响。列车最大轮重减载率随着二系空气弹簧垂向刚度、二系空气弹簧横向刚度、一系钢弹簧纵向刚度、二系横向减振器阻尼的增加而减少。

图9 悬挂系统参数变化对头车最大轮轨垂向力与轮重减载率的影响
当二系空气弹簧垂向刚度悬挂参数变化时,轮轨垂向力变化明显,随着横风的不断加载,头车一位轮对左右车轮的轮轨垂向力发生明显变化,如图10所示,迎风侧车轮随着风载荷的增加而减载,背风侧车轮随着风载荷的增加而增载。由公式(1)可知,轮轨之间垂向相对位移是列车轮轨垂向力的重要影响因素之一,公式(2)和(3)表明轮重减载率的变化是由对应的轮轨垂向力变化导致的。头车一位轮对左右车轮、头车转向架和头车车体的抬升量变化曲线如图11所示。高速列车在未加气动载荷之前抬升量稳定,在2s时期施加气动载荷之后升量急剧提高,前后到达顶峰后减少,之后增加到一定范围趋于稳定。

图10 二系空气弹簧垂向刚度变化对头车一位轮对轮轨垂向力影响
中央悬挂系统参数的变化会影响整个中央悬挂系统的功能,第一不能很好的将车体的重量以及载荷比较均衡地传递给各个轮轴,第二对于缓和冲动和衰减振动的能力有所降低,特别是列车在横风环境等复杂工况下运行时。高速列车在横风环境下运行时,二系空气弹簧垂向刚度变化会影响整个中央悬挂系统的功能,当参数变为标准值的50%时,车体的抬升量发生变化,其最大值由标准参数下的40.8mm增加到56.5mm,车体往上移了38.72%,在车体的带动下,转向架的抬升量也随之发生变化,转向架1抬升量由3.85mm增加到4.02,而转向架2抬升量由2.32mm减少到2.01mm。图12为高速列车动力学模型的轮轨踏面图,二系空气弹簧垂向刚度的变化会影响左右车轮的抬升量,在横风作用下车轮向迎风侧横移,由于踏面锥度迎风侧车轮与钢轨接触点向下移动,背风侧车轮与钢轨接触点向上移动,即轮轨之间的垂向位移发生变化,最终导致轮轨垂向力发生变化。


图12 高速列车动力学模型的轮轨踏面图
4 结 论
(1)头车一位轮对左右两个车轮的脱轨系数最大值随二系空气弹簧垂向刚度、横向刚度;一系钢弹簧垂向刚度、横向刚度的增加而减少,其中二系空气弹簧垂向刚度变为标准值的50%时,头车一位轮对迎风侧车轮的最大脱轨系数达到1.38,大于安全阈值0.8,列车在运行过程中有脱轨的风险。
(2)轮轴横向力会随着二系空气弹簧垂向刚度、一系钢弹簧垂向刚度、一系钢弹簧横向刚度的增加而减少;随着一系钢弹簧纵向刚度的增加而增加,这是由于轮对、转向架、车体的横移量发生变化,导致转向架分配在车轮上的载荷发生变化,最终造成轮轴横向力发生变化。
(3)列车最大轮重减载率随着二系空气弹簧垂向刚度、二系空气弹簧横向刚度、一系钢弹簧纵向刚度、二系横向减振器阻尼的增加而减少;轮轨垂向力会随着二系空气弹簧横向刚度、一系钢弹簧纵向刚度、二系横向减振器阻尼的增加而减少;随着一系钢弹簧横向刚度、一系钢弹簧垂向刚度的增加而增加,主要是由于悬挂参数变化导致车轮与钢轨之间的相对位移变化使轮轨垂向力变化。
[1] SUZUKI M. Aerodynamic characteristics of train/ vehicles under cross winds[J]. Journal of Wind Engineering and IndustrialAerodynamics, 2003, 91 (1-2): 209-218
[2] DIEDRICHS B, SIMA M, ORELLANO A. Crosswind of a high-speed train on a high embankment[J]. J. Rail and Rapid Transit, 2007, (221): 205-225.
[3] COOPER R K. Tests on a 1/5th APT-P in the MIRA wind tunnel[J]. British Rail Research Division Technical Memorandum TMAERO 28, 1978.
[4] THOMAS D, BERG M, DIEDRICHS B, et al. Rail vehicle response to lateral carbody excitations imitating crosswind[J]. Journal of Rail & Rapid Transit, 2015, 229 (1): 34-47.
[5] THOMAS D, DIEDRICHS B, BERG M, et al. Dynamics of a high-speed rail vehicle negotiating curves at unsteady crosswind[J]. Journal of Rail & Rapid Transit, 2009, 1 (6): 1-13.
[6] KIM M S, KIM G Y, KIM H T, et al. Theoretical cross- wind speed against rail vehicle derailment considering the cross-running wind of trains and the dynamic wheel- rail effects[J]. Journal of Mechanical Science & Technology, 2016, 30 (8): 3487-3498.
[7] 李振, 翟婉明, 赵春发, 等. 横风环境中复线路堤上高速列车的气动性能[J]. 铁道车辆, 2011, 49 (11): 1-5, 47.
[8] 龙苏琴. 高速列车不同路况横向气动性能仿真研究[J]. 机电一体化, 2017, 23 (4): 3-8, 34.
[9] 任尊松, 徐宇工, 王璐雷, 等. 强侧风对高速列车运行安全性影响研究[J]. 铁道学报, 2006, 28 (6): 46-50.
[10] 王开云, 孟宏, 翟婉明. “天梭”号电力机车参数优化及动力性能仿真分析[J]. 机车电传动, 2003, (6): 5-8, 12.
[11] 程冰. CW-200K型转向架结构改进和悬挂参数的优化研究[D]. 北京: 北京交通大学, 2005
[12] 池茂儒, 张卫华, 曾京, 等. 高速客车转向架悬挂参数分析[J]. 大连交通大学学报, 2007, 28 (3): 13-19.
[13] 崔涛, 王琰, 吴会超, 等. 高速列车悬挂参数全局优化方法[J]. 机车电传动, 2015, (1): 15-18.
[14] 董锡明. 近代高速列车技术进展[J]. 铁道机车车辆, 2006, 26 (5): 1-11, 62
[15] 刘宏友. 高速列车中的关键动力学问题研究[J]. 中国铁道科学, 2004, 25 (1): 137-139.
[16] 陈华斌, 金鼎昌, 古滨. 高速万向轴式动力车转向架的参数研究[J]. 西南交通大学学报, 1998, 33 (2): 46-51.
[17] 周鹏. 横风下高速列车悬挂系统参数优化设计[D].西南交通大学, 2019.
[18] 全国文献工作标准化技术委员会第七分委员会 (GB/T 5795—1986) 中国标准书号[S]. 北京: 中国标准出版社, 1986.
Effect of Suspension-system Parameters on Crosswind Stability of High-speed Trains
ZHOU Peng1, CHANG Cheng2, LI Tian2, QIN Deng2
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China;2. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610036, China)
The change in the train suspension-system parameters affects the safety and stability of its operation, especially in complex operating environments such as under crosswind. For a certain type of electric multiple unitin China, a numerical simulation was performed to investigate the aerodynamic characteristics of a train under crosswind and to study the influence of the relative standard value of the suspension-system parameters on the safety and stability of operation. Research indicated that the derailment coefficient of the first wheelset of the head vehicle decreases with the increase in the vertical and lateral stiffness of the air spring of secondary suspension as well as the lateral and vertical stiffness of steel spring of primary suspension. The wheelset lateral force decreases with the increase in the vertical stiffness of the air spring of secondary suspension, as well as the lateral and vertical stiffness of steel spring of primary suspension. The wheel unloading rate decreases with the increase in the vertical and lateral stiffness of the air spring of secondary suspension, longitudinal stiffness of the steel spring of primary suspension, and damping of the lateral damper in secondary suspension. The wheel–rail vertical force decreases with the increase in the lateral stiffness of the air spring of secondary suspension, longitudinal stiffness of the steel spring of primary suspension, and damping of the lateral damper in secondary suspension, along with the increase in the lateral and vertical stiffness of the steel spring of primary suspension.
suspension system; vehicle system dynamics; crosswind safety; high-speed train
1672-4747(2020)04-0083-10
U270.1+1
A
10.3969/j.issn.1672-4747.2020.04.011
2020-12-12
周鹏(1991—),汉族,安徽淮北人,西南交通大学助教,硕士,研究方向为车辆系统动力学、空气动力学等,E-mail:398097277@qq.com
周鹏,常城,李田,等. 悬挂系统参数对高速列车横风运行安全性的影响[J]. 交通运输工程与信息学报,2020, 18(4): 83-92
(责任编辑:刘娉婷)
