仿生巡检机器人越障性能分析
2020-12-24苏卫华祁宇明刘朝华张世月
谢 兵,苏卫华,祁宇明,刘朝华,张世月
(1.天津职业技术师范大学机械工程学院机器人及智能装备研究院,天津300222;2.天津(滨海)人工智能创新中心,天津300457;3.军事科学院国防科技创新研究院,北京100071)
0 引言
移动机器人可以在地震、战场救援、核辐射等危险环境替代人类作业,以及应用于日常生活中减轻人类的劳作负担,因此得到了广泛的关注和研究[1]。仿生巡检机器人是通过分析自然界生物运动机理、结合巡检作业环境设计的一种服务于特殊环境并基于移动机器人本体机构的智能机器人。其中,轮腿式移动机器人具有较强的稳定性和越障能力,因此一定程度应用于巡检、救援以及相对恶劣的环境中[2]。优异的机动性能、稳定性能以及较强的越障性能是评价移动机器人性能的准则和重要指标[3]。目前,国内外学者针对移动机器人越障性能进行了大量研究。李秉宣等[4]提出了基于稳定性指标的弧腿式搜救机器人越障与步态研究方法;刘远凯[5]研究了可变形车轮攀爬台阶的能力;孙筵龙等[6]、Chen 等[7]对轮腿式机器人爬台阶过程中姿态与控制进行了分析;Kim等[8]对轮式机器人翻越凸台障碍的能力及倾翻稳定性进行了研究;Chou 等[9]分析了轮式机器人不同翻越姿态下攀越台阶的能力。以上均是对机器人爬越台阶、凸台、沟壑等典型场景下的越障能力进行的研究,对机器人翻越管道障碍的研究极少[10]。在城市救援环境中,为了保证机器人能够顺利翻越管道完成巡检任务,掌握机器人翻越管道障碍的能力是必要的。
本研究基于仿生巡检机器人,针对城市救援环境中存在的管道障碍进行越障性能分析。以仿生巡检机器人翻越管道阶段不发生滑移、倾翻等为稳定条件,根据静力学以及机器人运动机构几何约束建立仿生巡检机器人翻越管道能力的理论分析模型,选择半径r=30 mm 的管道进行机器人越障理论分析,得到机器人在典型阶段下受力与机器人角度之间的关系以及机器人在各阶段中稳定翻越的最大可行高度,从而确定机器人稳定翻越管道的最大高度值。
1 机器人翻越管道过程分析
1.1 翻越管道位姿分析
仿生巡检机器人翻越管道的位姿变化如图1所示。
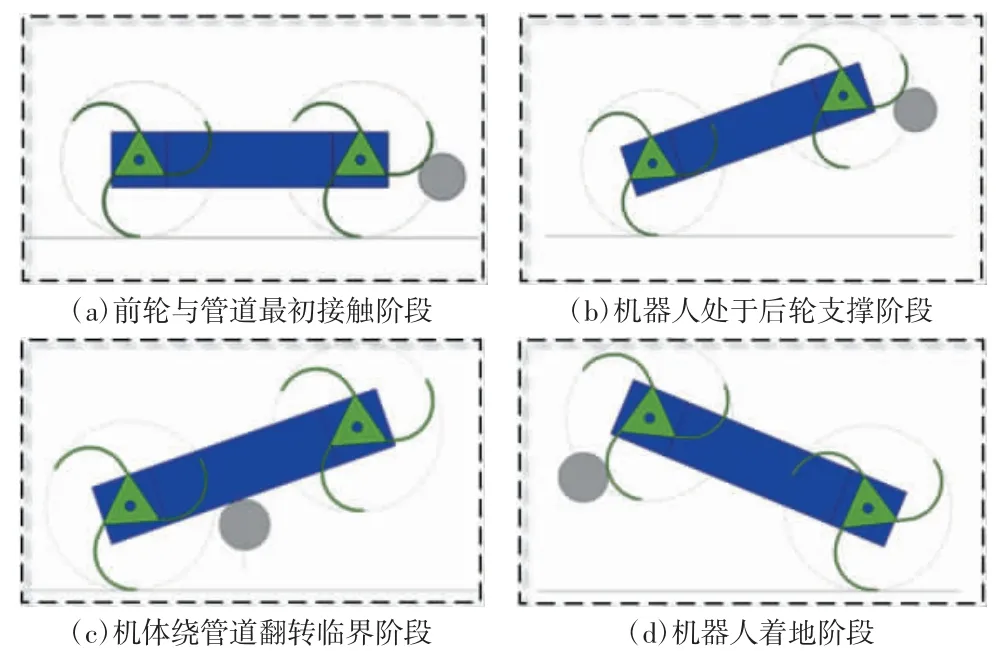
图1 仿生巡检机器人翻越管道位姿状态
仿生巡检机器人翻越管道的最大高度为不同位姿下所能达到的最大高度中的最小值,且需保证巡检机器人各位姿不发生滑移、倾翻等失稳状态,因此对机器人翻越管道过程位姿状态进行分析。
1.2 仿生巡检机器人结构参数
本文主要基于自制的仿生巡检机器人样机进行相关实验,机器人主要由机体、仿生腿(轮)等组成,假设仿生巡检机器人的重心位于机身的几何中心,则其基本参数为:两轮之间的中心距离l=364 mm,轮半径R=120 mm,整机质量m=24 kg,重心距机身下表面距离h=50 mm。选择半径r=30 mm 的管道作为障碍,取轮与管道之间的摩擦系数μs=0.8[11],根据轮与管道的交互力关系分析[12-14],可以得到轮与管道接触的等效摩擦力与等效支持力的最大比值μmax=1.58。
1.3 机器人翻越管道过程理论分析
(1)前轮与管道最初接触阶段。
仿生巡检机器人在翻越管道过程中机器人前轮初次接触管道障碍,如图2 所示。
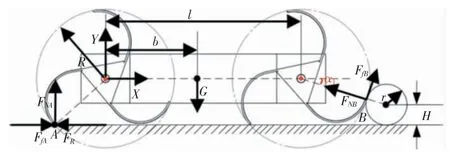
图2 前轮与管道最初接触阶段
根据图2 中几何关系,管道的中心离地面的高度H 可以表示为
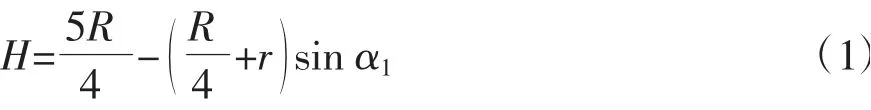
假设机器人在前进的过程中横向没有滑移存在,地面轮式移动方式中,有效牵引力表示为

式中,μx为轮与地面之间的摩擦系数。
本文主要考虑机器人的几何通过性,忽略机器人前进过程中内部阻力的影响,因此机器人受到的主要阻力为轮与地面之间的滚动摩擦力。机器人前进阻力FR表示为

式中,μτ为机器人行驶过程中的阻力系数,本研究中取μτ=0.015[11]。
根据力和力矩平衡原理分析得

为保证仿生巡检机器人前轮能够顺利地翻越管道,不发生滑移失稳的条件为:B 点处受到的等效牵引力与B 点处受到的等效支持力的比值小于等于轮与管道接触的最大比值μmax,即
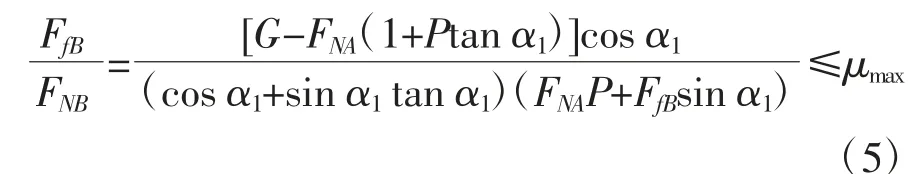
(2)机器人后轮支撑阶段。
仿生巡检机器人在前轮翻越管道障碍的同时机身与地面呈一定角度,仅机器人后轮与地面接触并起支撑作用,如图3 所示。
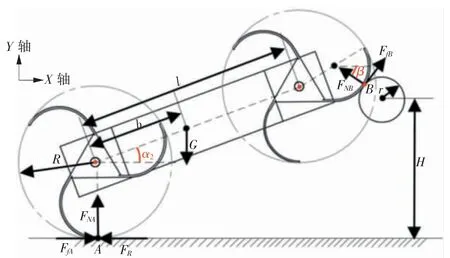
图3 后轮支撑阶段
根据图3 中几何关系,管道的中心离地面的高度H 可以表示为
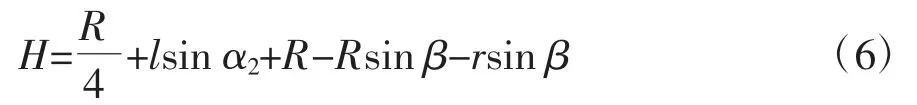
为保证仿生巡检机器人前轮能够顺利地翻越管道,应该保证在B 点不发生滑移失稳现象,根据力与力矩平衡原理分析得
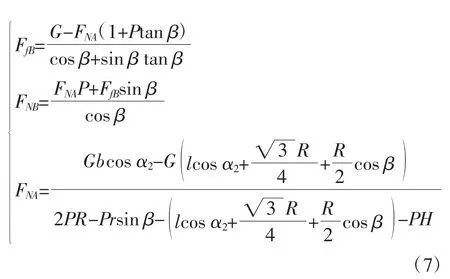
因此,机器人不发生失稳的条件为:机器人重心的投影位于机器人与地面和管道接触点之间,即(3)机体绕管道翻转临界阶段。
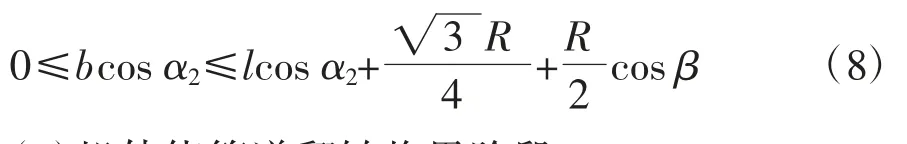
对于不同半径的管道,在惯性力与摩擦力作用下,仿生巡检机器人机身与管道发生直接接触并实现翻转,此时到达翻转临界姿态,即机器人的重心与管道接触点处于同一直线上,机器人后轮刚好离开地面,如图4 所示。
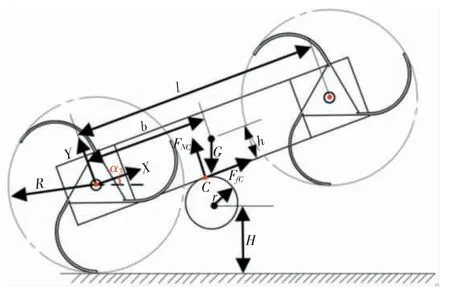
图4 机体绕管道翻转临界阶段
根据图4 中几何关系,管道高度与机器人仰角之间的关系为
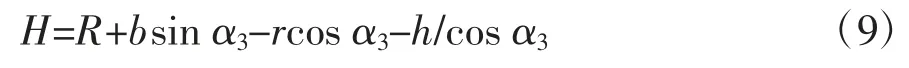
随着机器人攀爬管道的仰角不断增加,机器人会出现后翻的迹象,为防止机器人此过程出现后翻,需要满足倾翻稳定性,即

(4)机器人翻越管道着地阶段。
在翻越管道着地阶段,仿生巡检机器人在翻越管道着地前的瞬间易发生失稳状态,因此选取此瞬间作为机器人着地阶段中关键姿态,如图5 所示。
此位姿下管道的中心离地面的高度可以表示为

图5 机器人前轮着地阶段

仿生巡检机器人在前轮着地的瞬间要保证后轮与管道接触不出现打滑现象,需满足≤μmax,即

同理,根据重心投影原理可以得到机器人着地不倾翻的稳定条件为

2 机器人翻越管道过程的仿真分析
(1)前轮与管道最初接触阶段。
机器人在前轮管道最初接触阶段,根据公式(5)可知,偏转角α1≥32°满足机器人翻越稳定条件;由图6 可知,越障的高度H 随着偏转角α1的增大而减小。因此,α1=32°时,机器人翻越达到最大高度H=118.0 mm。
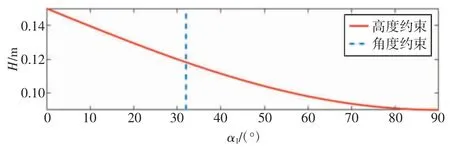
图6 前轮与管道最初接触阶段
(2)机器人处于后轮支撑阶段。
机器人机体处于后轮支撑阶段时,根据公式(7)、(8)可知,不发生失稳需满足β≥32°;若不考虑相关外界因素,由图7 可知,机器人的越障高度随着仰角α2的增加而增大,理论情况下当α2=90°,机器人能翻越最大高度H=434.5 mm。
(3)机体绕管道翻转临界阶段。

图7 机器人机体处于后轮支撑阶段
由图8 可知,机器人能够翻越管道离地面的最大高度H=164.7 mm,仰角α3=56°。
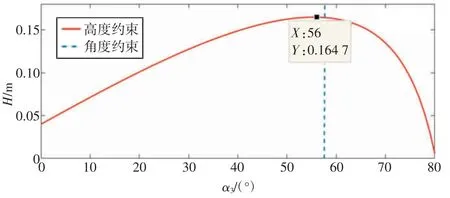
图8 机体绕管道翻转临界阶段
(4)机器人翻越管道着地阶段。
机器人在翻越管道着地阶段,由公式(12)可知,不同的着地夹角γ1可以得到不同的越障高度,在γ1=0°时,机器人越障的高度达到极限值。因此,本文以γ1=0°进行机器人翻越管道前轮着地阶段分析,如图9 所示。由图9 可知,机器人不发生失稳需满足β1≥33°,机器人的越障高度随着俯角α4的增加而增大,理论情况下当α4=90°,机器人能翻越最大高度H=633.9 mm。
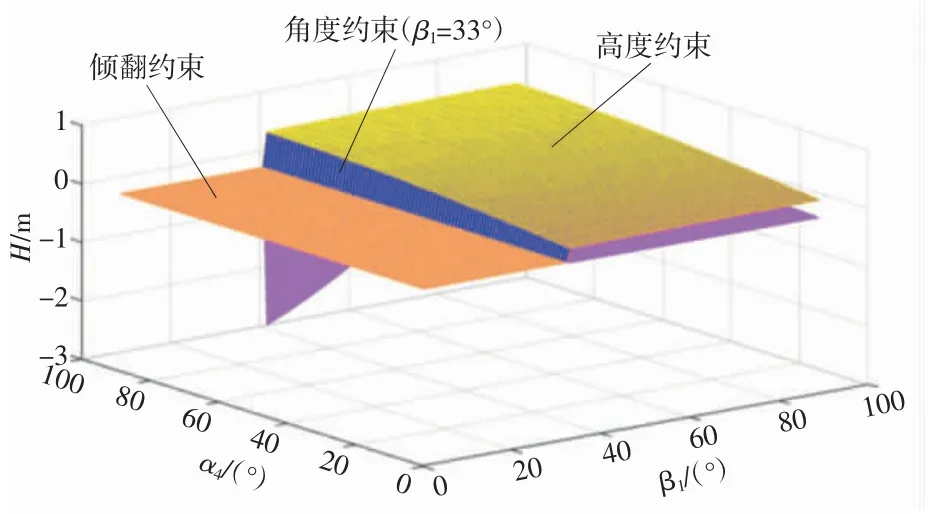
图9 机器人翻越管道着地阶段
根据上述结论可知,仿生巡检机器人在不同位姿下翻越半径r=30 mm 管道的最大理论可行性高度H=118.0 mm。
3 机器人翻越管道过程的实验分析
为了进一步验证仿生巡检机器人的越障性能指标[12,15],选择半径r=30 mm 的管道搭建实验平台进行相关实验,实验样机如图10 所示,最终得到各阶段“理-实”越障高度值对比,详见表1。通过实验验证可知仿生巡检机器人能够翻越半径r=30 mm 的管道,且最大可行高度H=120 mm。

图10 仿生巡检机器人实验样机
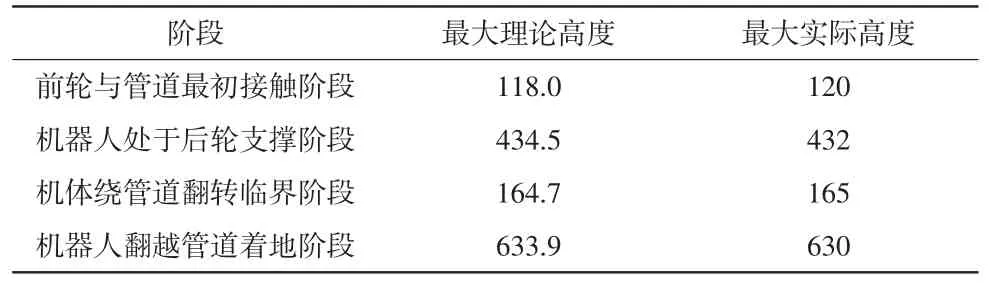
表1 各阶段下“理-实”越障高度值对比单位:mm
4 结论
本文以城市救援环境中存在的管道障碍为背景、仿生巡检机器人为本体,进行机器人翻越管道障碍性能分析。建立机器人翻越管道过程理论分析模型,得到仿生巡检机器人在典型阶段下的等效牵引力、等效摩擦力、等效支持力与机器人角度关系,且机器人翻越半径r=30 mm 管道的最大可行高度H=120 mm,对改进仿生巡检机器人在翻越管道能力以及提升巡检机器人智能化程度具有重要意义。
由于城市救援环境的复杂性,本研究仅针对仿生巡检机器人定速下翻越管道可行性高度进行分析与仿真实验,未来将从以下3 个方面进行进一步研究:(1)机器人在不同运行速度下翻越管道的性能;(2)机器人与管道之间的弹性接触对翻越管道的影响;(3)机器人翻越不同形状障碍的运动特性。
