关于迭代算子DkGk的局部与全局的Lp-加权积分不等式

*李群芳，李华灿

(1.赣州师范高等专科学校数学系，江西，赣州341000；2.江西理工大学理学院，江西，赣州341000)

0 引言

本文目的是研究微分形式上迭代算子D kGk的Lp-加权积分不等式。近年来，微分形式的算子理论作为调和分析的一个重要内容引起了广大学者的研究兴趣，并取得了丰硕的成果。2003年，Ding S S[1]得到作用于光滑微分形式上Green 算子G的Poincaré-型如下形式的范数不等式

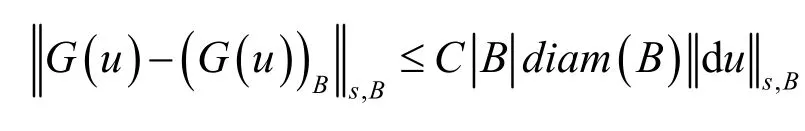
其中B为Rn的子区域Ω 上的球体。2004 年，Wang Y 和Wu C X[2]合作证明了作用于满足非齐次A-调和方程的微分形式上的关于Green 算子G的加权Poincaré-型不等式。Xing Y M 和Ding S S在文献[3]中给出了Green 算子的Lipschitz 范数和BMO范数比较定理。文献[4]进一步得到Lφ-平均域上Green 算子的全局的Orlicz 范数估计。2016 年，Ding S S, Shi G N 和Xing Y M 在文献[5]中首次引出迭代算子D k Gk并证明了迭代算子的Lp-高阶积分不等式，其中D为Dirac-算子，k为一正整数，更多关于微分形式上的算子理论成果可参见文献[6-12]。本文以文献[5]中迭代算子D kGk的Ls-范数估计为基础，证明Rn的子区域Ω 上局部与全局的(λ1,λ2;E)-权Lp-积分不等式。该结果将进一步丰富迭代算子的积分范数理论，同时为迭代算子的其他理论的研究提供可靠的研究工具。

1 引理与相关定义

2 主要结论

(3)如果W中存在有限个球体Bj不符合σBj⊂Ω 的情形(j=1,2, …,l,σ>1)，则只需重复(2)中的过程有限次即可。

综合(1)(2)(3)，定理2.2证毕。