脑洞大开 一题多解
2020-12-24阮萍扬
阮萍扬
(福建省泉州师范学院附属中学 福建 泉州 362000)
2019年泉州市二检中,有一道题吸引了笔者的眼球,乍一看切入点不好找,思路不清晰,但仔细思考后会发现有多个角度可以入手分析,随着思考广度的不断拓展,一题多解,脑洞大开。
题目:如图,在△ABC中,内角A,B,C的对边分别是a,b,c,a+b=5,(2a+b)cosC+ccosB=0,若点D为AB的中点,∠ACD=30°,求a,b的值。
1.向量方向

总结:向量用来解三角问题,经常要用到模长平方,向量的夹角公式,或向量点乘的几何意义、极化恒等式等等,这是一个研究解三角形问题的方向,是一种常见的方法。
2.解三角形方向
总结:此题的参考答案解法也非常漂亮,利用△ACD和△BCD面积相同可以轻易得到b=2a;参考答案还给了另外一种解法,在△ACD对∠ADC用正弦定理;在△CBD对∠CBD取正弦值;联立后,即可以得到b=2a。而笔者的这个解法主要受到2017年全国卷1卷三角函数大题的启发,条件可以二次应用,得到新的条件,这也不失为一种好的解法。解三角形问题,用正余弦定理、面积公式等,这种解法中规中矩,套路化模式化是最重要的一种基本方法。
3.解析几何方向
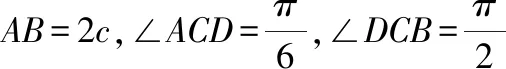
总结:利用建系,运用代数的方法解决几何问题,这是解析几何神奇之处,常常有化难为易,化繁为简的功效,并且思路简单,入手容易,是解决三角问题的好方法。解法5,利用条件a+b=5,构造一“椭圆”,再利用椭圆的性质去解决问题。这种解法在此例中运算量较大,“小题大做”,但巧在构造的模型。值得一提的是,另外一种常见构造结构圆,也是解决三角问题的一种好模型好方法。
4.平面几何方向
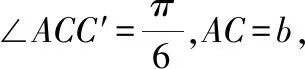
总结:利用平几知识点解决问题,是非常好的一个思路,并且解法不唯一。此题也可以过点A做直线与BC相平行,利用中位线解决问题。也可以过点D做AC的垂线,用相似解决。平面几何的分析方法越来越重要,也是近几年的国考卷中常见的命题手法。
5.联立方程解方程组方向

总结
假设未知数求解未知数,假设两个变量,那么只需要找到两个等式,联立求解即可。此题解法,刻意的选择“公差”作为其中一个变量,计算过程略显麻烦。实际上对于变量的选择还可以有其它选择,可设边长,可设角度,有了变量再去寻找等式。这种方法较为“笨重”,尽管计算量大,但思简单,入手容易,因此成为解决三角问题,最值问题常用解题策略。
