基于改进鲸鱼优化算法的阵列单元失效校正

孟宪猛，蔡翠翠

(1.安徽博微长安电子有限公司，安徽 六安 237012；2.目标探测与特征提取安徽省重点实验室，安徽 六安 237012；3.皖西学院 电子与信息工程学院，安徽 六安 237010)

0 引言

阵列天线是由若干天线单元按照一定方式排列和激励形成的电磁波辐射源，具有高增益、多波束、低副瓣、快速扫描等特点，被广泛应用于现代雷达系统[1]。随着雷达系统的智能化、多功能化，阵列天线结构日益复杂，天线阵元数目可达数千个，增加阵元失效的概率。由于器件老化、受外界物理损坏等因素，会导致天线阵列单元失效，造成天线副瓣电平升高、波束变宽和天线增益下降等[2-4]，影响雷达系统的探测性能。同时，电磁脉冲、高能微波武器的强电磁脉冲入侵造成阵列天线阵元损伤，影响雷达系统的性能[5]。失效阵元维修更换的时间较长，特别是战场环境下，无法进行及时修复。因此，通过对阵列天线失效阵元的校正，优化配置剩余阵元资源，最大程度保证阵列天线性能，就显得尤为重要。

目前对于阵列天线失效校正的研究，主要通过智能优化算法进行剩余阵元优化，文献[6—7]利用遗传算法但算法在优化过程中易陷入局部最优。文献[8]利用粒子群算法对失效阵列天线进行优化，使失效阵元后的方向图得到校正，但算法在求解后期的收敛性能趋于饱和，易出现早熟现象。文献[9]利用布谷鸟优化算法对阵元失效进行校正，但易陷入局部最优，收敛精度低。文献[10]利用差分搜索算法对失效阵元进行校正，最大程度保证阵列天线的性能，但存在收敛精度低等问题。本文针对此问题，提出一种改进鲸鱼优化算法，在鲸鱼优化算法基础上，采用自适应权重加速算法收敛，结合差分进化策略，丰富种群个体信息，增强优化算法的全局收敛性，通过对优化剩余正常阵元，有效抑制阵列的副瓣电平，降低失效阵元对阵列天线性能的影响。

1 阵列天线模型

直线形阵列天线由于结构简单且易于实现，得到广泛应用。本文以直线阵列天线为例，研究阵元失效校正问题。对于N个单元等距均匀直线阵，假定每个阵元均各向同性，则阵列天线的归一化阵因子可以表示为[1]：

(1)

式(1)中，In为第n个阵元的激励电流；k为波数，k=2π/λ，λ为空间自由波长；dn、φn分别为第n个阵元的位置和相位；d为均匀线阵的阵元间距；u=cosθ，θ为射线方向与阵列轴线之间的夹角。

通过对阵列天线中剩余正常阵元激励的重配置，可以降低失效阵元影响，尽可能恢复阵列天线的性能，实现阵列天线的失效校正。为有效评价智能优化算法对阵元失效校正效果，结合天线最大副瓣电平和波束宽度，构建适应度函数为[5,11]：

Fitness=fSLL(θ)+k·fBW

(2)

fSLL(θ)=max[F(θ)]

(3)

fBW=max(0,|Wd-W|-0.05)

(4)

式(2)—式(4)中，k为权重系数；Wd、W为期望和计算的波束宽度。

2 改进鲸鱼优化算法

2.1 标准鲸鱼优化算法

鲸鱼优化算法是通过模拟座头鲸的捕食猎物行为而提出的一种新型元启发式算法，具有结构简单、调节参数少、局部寻优能力强等特点，主要包括猎物包围、气泡网攻击、搜索猎物三个阶段[12-13]。

1) 猎物包围

座头鲸根据识别猎物所在位置实现猎物包围，然而由于猎物的位置无法提前获知，所以在鲸鱼优化算法中，假设当前种群最优个体位置为最优目标点位置，其他个体均向最优位置调整。数学模型表示为：

X(t+1)=X*(t)-A·D

(5)

D=|CX*(t)-X(t)|

(6)

式(5)、式(6)中，t是当前迭代次数，X*(t)是当前最优个体位置向量，X(t)是当前个体的位置向量，A和C是系数变量，计算公式如下：

A=2ar1-a

(7)

C=2·r2

(8)

a=2(1-t/Tmax)

(9)

式(7)—式(9)中，r1和r2为[0,1]之间的随机数；a为控制参数，呈线性递减；Tmax为最大迭代次数。

2) 气泡网攻击

座头鲸吐气泡攻击猎物，主要分为收缩包围和螺旋位置更新，数学模型可以表示为：

① 收缩包围：通过系数变量A的控制参数a，实现对猎物的包围收缩。

② 螺旋位置更新：鲸鱼在包围猎物后，以螺旋式运动捕获猎物，其数学模型为：

X(t+1)=X*(t)+DP·eblcos(2πl)

(10)

式(10)中，DP=|X*(t)-X(t)|表示鲸鱼与猎物的距离，b表示对数螺旋形状常数，l是[-1,1]之间的随机数。

座头鲸在气泡网攻击猎物时，收缩包围和螺旋位置更新两种方式是同步的。在数学模型中，采用相同概率更新位置信息，可以表示为：

(11)

式(11)中，p为[0, 1]上的随机数。

3) 搜索猎物

座头鲸在气泡网攻击猎物时，还会随机搜索猎物。以变量系数A为基础，当|A|值大于1时，随机选取鲸鱼个体位置，调整寻优个体的位置信息，以增强算法的全局搜索能力，其数学模型表示如下：

X(t+1)=Xrand-A·D

(12)

D=|C·Xrand-X(t)|

(13)

式(12)、式(13)中，Xrand表示当前群体中随机选择的一个位置向量，X(t)为个体所在的位置向量。

2.2 改进的鲸鱼优化算法

标准鲸鱼优化算法主要通过调节变量系数A、C实现局部和全局寻优，而在优化复杂问题时，系数的调节依赖随机性，导致收敛速度慢、收敛精度低[14-15]。为解决这一问题，提出一种改进鲸鱼优化算法，该算法在标准鲸鱼优化算法基础上，引入自适应权重，提升局部寻优能力；同时结合差分进化策略，通过最优解的交叉、变异和选择，提升全局寻优能力。

2.2.1自适应权重

权重因子可有效平衡算法的局部寻优能力和全局能力[16]。对鲸鱼优化算法引入自适应权重，权值计算公式如下：

(14)

式(14)中，t为当前迭代次数，Tmax为最大的迭代次数。

鲸鱼优化算法增加自适应权重后，所包含猎物包围、气泡网攻击和搜索猎物的数学模型更新为：

X(t+1)=X*(t)-ω·A·D

(15)

X(t+1)=X*(t)+ω·DP·eblcos (2πl)

(16)

X(t+1)=Xrand-ω·A·D

(17)

2.2.2差分进化策略

差分进化是一种模拟生物进化算法，主要有变异、交叉和选择等操作[17-18]。具体过程为：在每次迭代结束后，对当前最优位置向量进行变异和交叉，得到新的位置向量，并进行适应度计算，如果求得新的适应度值小于最优位置向量，则用替换当前最优位置，否则继续下一次迭代。

1) 变异操作

变异操作是通过选取当前种群中较优的鲸鱼个体进行变异，扩大搜索范围，避免算法陷入局部最优，具体如下式：

Vi(t+1)=Xi(t)+F·(Xr1(t)-Xr2(t))

(18)

式(18)中，Vi(t+1)表示变异后的鲸鱼个体位置；F表示缩放比例因子；Xr1(t)-Xr2(t)表示当代鲸鱼个体位置的差异向量。

2) 交叉操作

交叉操作是通过产生一个随机数，并与比较交叉因子比较，判断是否产生新个体，具体如下式：

(19)

式(19)中，Ui(t+1)表示交叉后的鲸鱼个体位置，C表示交叉因子。

3) 选择操作

选择操作是将交叉后的个体位置与原始个体位置进行比较，根据适应度值大小决定是否采用新个体，具体如下：

(20)

2.2.3算法的实现步骤

改进的鲸鱼优化算法通过引入自适应权重和差分进化策略，有效提升局部寻优和全局寻优能力，具体步骤如下：

1) 初始化算法参数，设定种群个数N，最大迭代次数Tmax，对数螺旋形状常数b，随机数l，缩放因子F，交叉因子C等参数；

2) 在解空间内随机产生种群，计算适应度函数值，记录种群中适应度函数值最优的个体位置为最优位置；

3) 当p<0.5时，若|A|<1，通过式(14)更新鲸鱼位置信息；若|A|≥1，通过式(16)更新鲸鱼位置信息，计算个体的适应度函数值；

4) 当p≥0.5时，通过式(15)更新鲸鱼位置信息，计算个体的适应度函数值；

5) 利用式(17)对最优位置再进行差分进化，计算个体的适应度函数值；

6) 根据差分进化前后的适应度函数值，判断是否更新最优位置，若经过差分进化的个体适应函数值小于更新前个体适应函数值，则保留进化后的个体位置和适应函数值，否则舍弃进化后个体位置；

7) 判断算法是否满足最大迭代次数，若满足条件，输出最优值和最优个体位置，否则返回步骤2)继续搜索。

3 仿真实例

为验证所提出算法的有效性，通过实例进行仿真验证。

仿真实例1：对于线性阵列天线，单元数N=32，单元间距d=λ/2，天线波长λ=1，采用等幅度馈电，激励电流的相位为0，权重系数k为10，假定阵元3、11、18、24失效，阵元失效前后的天线方向图如图1所示，从图1中可以看出，阵元失效导致天线副瓣电平升高，方向图急剧恶化。

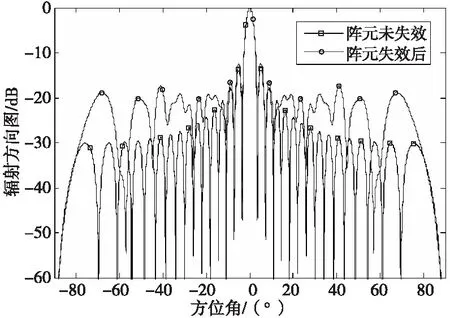
图1 阵元失效前后的方向图Fig.1 The antenna pattern before and after array element failure

采用改鲸鱼优化算法优化阵元激励幅度，对阵元失效后的天线方向图进行校正，并和标准鲸鱼优化算法、采用线性优化算法权值更新的粒子群优化算法优化结果进行比较。算法的初始参数设置为：种群个数为30，最大迭代次数为500次，对数螺旋形状常数b为1，缩放因子F为0.8，交叉因子C为0.9。

经过仿真，得到优化算法收敛曲线和优化后的阵列天线方向图如图2和图3所示，从图2中可以看出，改进的鲸鱼优化算法迭代进化优于标准鲸鱼算法；从图3中可以看出，阵元失效后天线最大副瓣电平为-12.46 dB，经过改进鲸鱼优化算法、标准鲸鱼优化算法和采用线性权值更新的粒子群优化算法校正后的方向图最大副瓣电平分别为-18.08、-17.34和-17.58 dB。

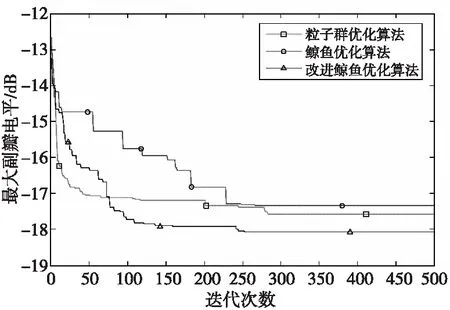
图2 算法的收敛曲线Fig.2 Convergence curve of the algorithm

图3 优化后的天线方向图Fig.3 The optimized antenna pattern

仿真实例2：对于线性阵列天线，单元数N=32，单元间距d=λ/2，天线波长λ=1，采用副瓣为-30 dB的切比雪夫加权馈电，激励电流的相位为0，假定阵元3、9、15失效，阵元失效前后的天线方向图如图4所示。从图中可以看出，阵元失效导致天线副瓣电平升高，方向图急剧恶化。

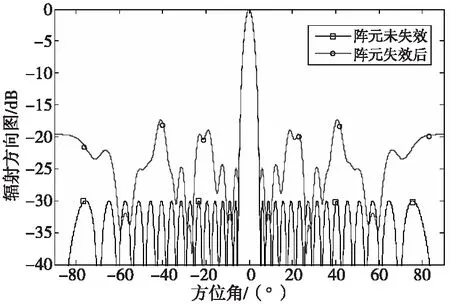
图4 阵元失效前后的方向图Fig.4 The antenna pattern before and after array element failure

通过优化阵元激励幅度实现方向图校正，优化算法的参数设置同实例1。

经过仿真，得到算法收敛曲线和阵列天线方向图如图5和图6所示，从图5中可以看出，改进的鲸鱼优化算法迭代进化优于标准鲸鱼算法；从图6中可以看出，阵元失效后天线最大副瓣电平为-17.34 dB，经过改进鲸鱼优化算法、标准鲸鱼优化算法和采用线性权值更新的粒子群优化算法校正后的方向图最大副瓣电平分别为-21.58、-19.32和-20.45 dB。

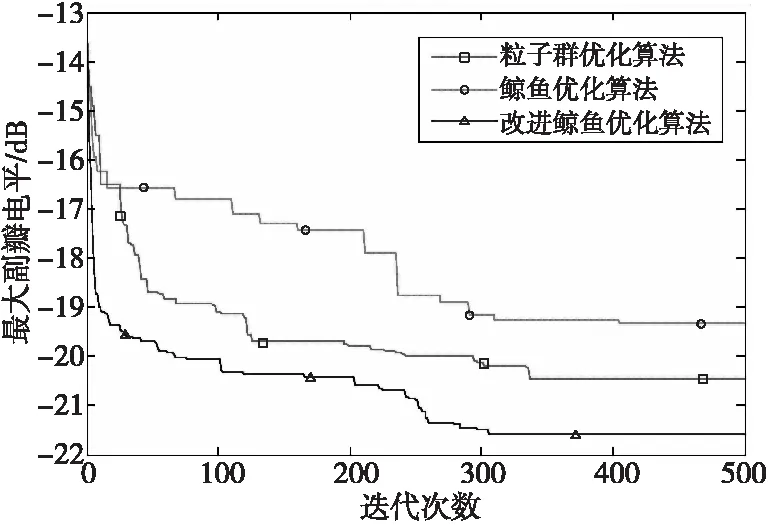
图5 算法的收敛曲线Fig.5 Convergence curve of the algorithm

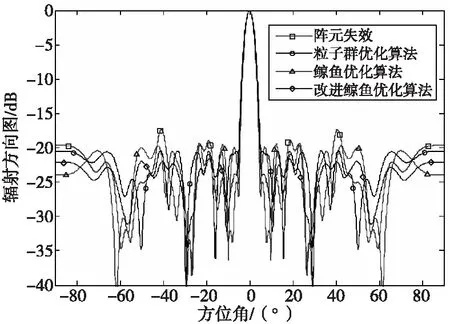
图6 优化后的天线方向图Fig.6 The optimized antenna pattern

由此可见，改进鲸鱼优化算法的收敛速度和收敛精度优于标准鲸鱼优化算法和采用线性权值更新的粒子群优化算法。

4 结论

本文提出了一种改进鲸鱼优化算法，用于阵列天线阵元失效校正。该算法在鲸鱼优化算法的基础上，引入自适应权重，提升局部寻优能力；同时结合差分进化策略，通过最优解交叉、变异和选择，提升全局寻优能力。仿真实例表明，改进鲸鱼优化算法能够有效抑制阵列的副瓣电平，降低失效阵元对天线性能的影响。