基于瞬时转速的旋转激光测量系统测角精度评价

任永杰，金云超，郭同闯，林嘉睿

(天津大学 精密测试技术及仪器国家重点实验室，天津 300072)

1 引 言

随着先进装备制造业的不断发展，大尺寸空间精密测量技术作为关键的工艺质量控制手段，已成为大型装备制造及精密工程安装的基础支撑技术之一。其中，大尺寸工件关键点坐标的精密、高效测量在大尺寸工件对接装配领域凸显出重要的现实意义[1-2]。常规大尺寸坐标测量系统以单站式球坐标测量系统最为典型，它对目标点的角度观测依赖光学码盘来完成。但基于点位对准的角度测量机理在面对空间多目标点测量任务时，始终无法摆脱目标点依次观测的测量模式，测量效率十分受限[3]。多基站旋转激光扫描方式的出现为角度测量提供了全新的传感方式，其核心理念为“以时间差测位置差”的时-空转换思想，以匀速旋转运动载体为媒介，由脉冲触发式测量取代机械对准式测量，赋予系统多目标快速扫描并行测量的能力，大大提高了测量效率，相关系统近年来发展迅速，应用十分广泛[4-5]。

目前，旋转激光测量系统测角精度的评价方式主要可分为整体测角精度评价和单环节误差分析。前者采用千分表打表法、多面棱体-自准直仪-多齿分度台组合检测装置、光电传感器与精密转轴搭建单站校准平台等方案进行精度评价[6-8]。这些方案较为全面地评价了系统整体测角精度，但由于融合了各环节的误差影响，难以对某个环节的误差进行具体量化。后者通常采用抽象建模的方式，从数模角度对该环节内部的多个误差影响因素展开研究，进而评价单环节误差[9-11]。但某些环节如电机伺服控制系统，本身各影响因素相互耦合，理论模型复杂，单独分析较为困难。匀速的机械扫描和场扫描(光场、电场)是基于时空转换思想实现高精度测角的重要基础[12]，以上两种方式忽视了作为空间-时间媒介的转速环节的重要性，若借助转速建立测角误差模型，则可避免建立复杂模型，在不引入其他误差环节影响的基础上，对与转速相关的误差环节进行着重分析，进而为提升系统的转速稳定程度及测角精度提供评判依据。

目前，瞬时转速稳定性评价指标的缺乏限制了对瞬时转速稳定程度的定量分析和优化。本文以天津大学精密测试技术及仪器国家重点实验室研制的制造空间测量定位系统(workshop Measurement Positioning System，wMPS)[4]作为实验平台展开研究，发射站内部的码盘作为电机转速控制系统的关键传感器，解析码盘脉冲序列并结合相关数字转速算法可计算得到转台转速。为了定量研究系统瞬时转速的稳定程度，基于对码盘脉冲和传统转速算法的研究，并结合系统测角精度影响因素的误差分析，引入“瞬时转速稳定度”作为瞬时转速评价指标。针对传统转速算法在使用低精度码盘时测速误差大的问题，提出一种基于脉宽误差补偿的瞬时转速算法，通过实验验证获得了测角精度和瞬时转速稳定度的相关性规律。

2 测角模型及误差分析

旋转激光测量系统一般由激光发射站、接收器、前端处理器和计算机组成，其角度测量原理如图1所示。激光发射站发射两相交激光扇面Plane 1和Plane 2激光发射站可抽象成质点。建立基站坐标系为OXYZ，定义Z轴为旋转轴，Plane 1和Z轴的交点为原点O，Plane 1上过原点且与旋转轴垂直的直线为X轴，根据右手定则确定Y轴。

基于上述模型，系统的测角过程为：系统发射站转台逆时针旋转，发射两束旋转扫描激光和一束同步脉冲激光，构建覆盖全周空间的三维角度测量场。接收器根据光电脉冲周期与发射站旋转周期的匹配关系识别信号来源。发射站内部的增量式码盘旋转一周触发一次同步光信号，如图2所示。T0时刻接收器在C位置处接收到同步光信号，以T0为初始时刻，在时刻t1，t2接收器位于相对位置C1，C2处，则相对初始位置转过的扫描角θ1，θ2可由扫描光-同步光相位差与转速乘积得到。

利用激光面扫描角θ1，2，结合两激光面的已知位姿参数(φ1，φ2，θoff)可计算接收球相对原点O的水平旋转角α和垂直旋转角β，最终利用单站方位角和多站角度交会原理实现空间坐标解算。

图2表示的角度测量原理中隐含了时空转换思想，作为空间角度差Δθ和时间差Δt的媒介，激光面扫描转速ω的稳定性会直接影响空间角度测量场的精度和分辨力。鉴于实际应用场合中对坐标测量的实时性要求，此类系统的工作转速常在千转每分钟以上，测量周期仅为几十毫秒，因此这里采用瞬时转速(Instantaneous Rotation Speed，IRS)来描述转台在单个测量周期内各观测点的旋转速度。目前，关于瞬时转速波动造成测角误差的研究较少，本文建立了转速波动模型以分析瞬时转速波动对测角精度的影响。由图2可知，瞬时转速波动会引起均匀时间间隔内转过的角位移量不均，导致角度测量误差。误差公式为：

(1)

其中：Δω是瞬时转速与平均转速的差值，t0是时间零点，t1为光平面扫过测量点的时刻，ω(t)为瞬时转速函数，ωm为平均转速。

以图3为例说明瞬时转速波动对测角误差的影响。t1～t2期间，理想情况下光平面应以转速ωm转过角度θ1，而实际瞬时转速ω(t)>ωm，实际扫描角为θ1+Δθ1，角度误差为Δθ1。t1～t2期间，ω(t)上下波动，导致t1～t2期间累积的角度误差被抵消。t2时刻角误差对比t1时刻的角度误差减小。

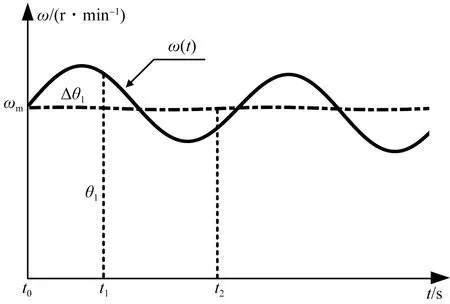
图3 转速误差模拟

由上述分析可知，瞬时转速引起的测角误差与时间零点t0和扫描时刻t1，t2相关，即与激光发射站和接收器的相对位置相关；另外，在测量周期内，瞬时转速与平均转速的偏差值减小或瞬时转速围绕平均转速上下波动的频率增大都会降低瞬时转速波动导致的测角误差。

3 瞬时转速稳定度与瞬时转速算法

3.1 瞬时转速稳定度

由于瞬时转速的波动幅值和波动频率共同影响瞬时转速稳定程度，本文引入瞬时转速稳定度(Instantaneous Rotation Speed Stability，IRSS)概念表征系统的瞬时转速稳定程度[13]。定义系统的IRSS为瞬时转速与平均转速在某时间内包围的角位移，其数学表达式如下：

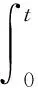
(2)

其中：ω(t)为瞬时转速，ωm为平均转速，T为测量周期。IRSS与误差分析中式(1)的角度旋转误差的计算方式相同，但与时间零点t0和目标点被扫过的时刻t1，t2无关，表征的是瞬时转速波动幅值和波动频率耦合的一种属性。

IRS是计算IRSS的必要条件。基于码盘的传统转速算法主要有M法、T法、M/T法和一些特定转速测量场景下的优化算法[14-16]。利用wMPS发射站内部的码盘脉冲，基于传统M/T法计算得到IRSS约为600″，与实际测角精度评价实验的误差结果不符[4]。

传统M/T法计算转速时以脉冲计数值换算角度位移量的方式建立在理想、均匀的码盘脉冲基础上。光栅刻线精度和安装等因素导致码盘的脉宽均匀性变差，直接影响传统M/T法的转速测量精度，进而影响相应的角度误差。实验中使用的增量式码盘标称精度为16′，使用示波器实际检测码盘的多组脉冲宽度时发现脉宽均匀性较差，脉宽标准差可达平均值的18%。传统转速算法在使用低精度码盘时的测速误差较大，亟需减小码盘脉宽误差的影响以提升转速测量精度。

3.2 基于脉宽误差补偿的瞬时转速算法

为补偿码盘脉宽误差造成的瞬时转速测量误差，提出基于脉宽误差补偿的瞬时转速算法，经标定过程得到码盘的真实脉宽比例，在角位移计算环节补偿脉宽误差以提升测速精度。一般使用高精度的测角仪器可精确标定码盘的脉宽，现采用一种简易的标定方法，仍可以获得不错的补偿效果。

为保证脉宽比的正确性和补偿算法的有效性，标定时采用以下方法：整机旋转时负载采用最大转动惯量的旋转头架，以抑制电机转速的波动，提升转速的稳定性；采集多圈数据计算多组脉宽比值取平均值，以减小测量随机误差；提升示波器的采样频率，即采用高频时钟计数，以减小计时误差。根据电机的最大扭矩和负载转动惯量计算得到，电机在旋转一圈的时间内转速波动不超过±1 r/min，标定时转速波动造成的影响可忽略。

如图4所示，规定转过N个码盘脉冲时计算一次转速，将一圈角位移分割成p段角位移，其中p=R/N。确定N的原则有：N可被R整除；平均转速下，旋转一周的转速考察点个数p应大于25(传统算法在1 850 r/min转速下旋转一周约产生30个瞬时转速值)。利用每段角位移中N个脉冲的脉宽比例，将每段角位移补偿为真实角位移，获取该角位移段起始和结束时刻值计算该角位移段内的平均转速，作为该观测点的瞬时转速。

图4 瞬时转速算法原理

以计算第一个瞬时转速为例，第一段角位移的表达式为：

(3)

其中：X为转速计算的第一个位移段，R为码盘分辨率，Ki为标定获得的每个脉冲的脉宽比值。转过这段位移的时间为：

T=m2/fc，

(4)

其中m2为在N个脉冲时间内计数器的计数值(即示波器采样次数)。结合式(3)和式(4)得瞬时转速为：

(5)

已知60fc/R为一个常量，令α=60fc/R，式(5)可改写为：

(6)

由于计时T的启停由码盘上升沿触发，位移无分辨率误差，算法的分辨率取决于时钟脉冲计数变化±1，算法分辨率为：

(7)

(8)

则优化后的转速算法测速误差为：

(9)

4 实 验

4.1 瞬时转速稳定度测量

为验证基于脉宽误差补偿的瞬时转速算法的正确性，进行了图5所示的瞬时转速稳定性测试。

如图5所示，系统轴系和转台完成转子动平衡后固定于光学平台台面，经驱动器控制软件调节PID参数最优，给定转速控制转台旋转。使用示波器(Keysight MSOS254A)采集增量式码盘的A，B，Z三相信号。首先设置采样率为50 MHz采集配备大惯量转台的发射站码盘数据进行标定数据采集。随后更换正常惯量转台并采集码盘数据，最后计算出IRS和IRSS。

图5 瞬时转速稳定度测量

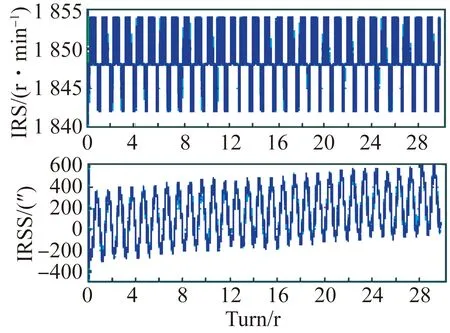
图6和图7为两种发射站使用M/T法、脉宽相同的补偿算法(即将脉宽数组K全设为1)和使用标定脉宽的补偿算法得到的IRS曲线和IRSS曲线。由图可知，标定脉宽的补偿算法在不同类型的发射站上均获得了较好的效果。图6(a)和6(b)对比表明，M/T法计算的IRS波动为±4.5 r/min，IRSS为600″左右，而采用本文设计的按脉冲数分段计算位移的算法，在不考虑脉宽误差时，对比M/T法仅在转速分辨率上有所提升。对比图6(b)和6(c)，经标定脉宽误差补偿后计算的IRS波动为±0.25 r/min，IRSS降至±4″，表明了脉宽误差补偿对提升测速精度的有效性。以上3种转速算法中，基于脉宽误差补偿的IRS算法的测速精度最优，IRSS数值最合理。

4.2 验证实验

为研究旋转激光测量系统的测角精度与IRSS的关系，验证实验如图8所示。在8 m×8 m×2.5 m的空间中布置两个发射站和24个控制点和16个测量点，分别使用激光跟踪仪(Leica AT403)和wMPS测量这些点的坐标。激光跟踪仪用于获取精确的空间三维坐标并与wMPS测量点的坐标进行比对，其测角误差为±15 μm+6 μm/m[17]，由于测角度盘误差、轴系加工误差等因素的存在[18]，跟踪仪在水平、垂直方向的测角精度存在一定的差异。计算得到坐标误差并反算出单站测角误差，结果如图9所示。

(a)M/T法(a)M/T method

(b)脉宽相同的补偿算法(b)Compensation method with same pulse width

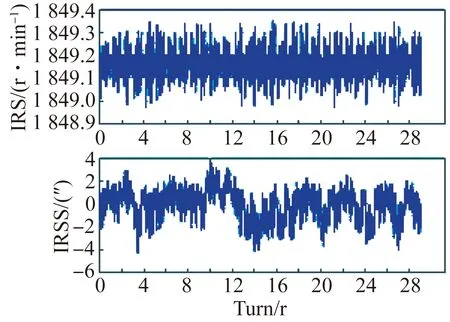
(c)标定脉宽的补偿算法(c)Compensation method with calibrated pulse width

(a)M/T法(a)M/T method

(b)脉宽相同的补偿算法(b)Compensation method with same pulse width

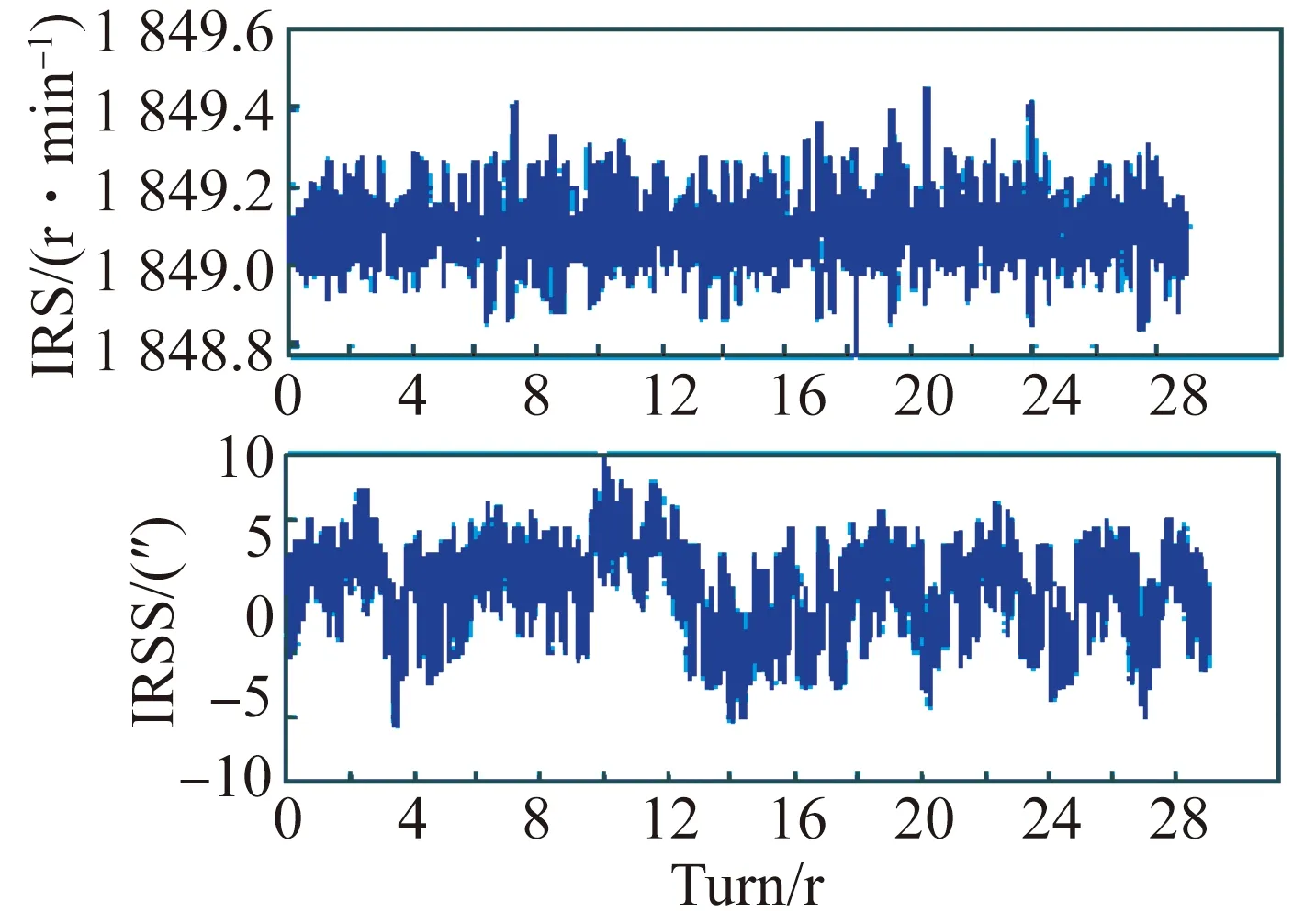
(c)标定脉宽的补偿算法(c)Compensation method with calibrated pulse width

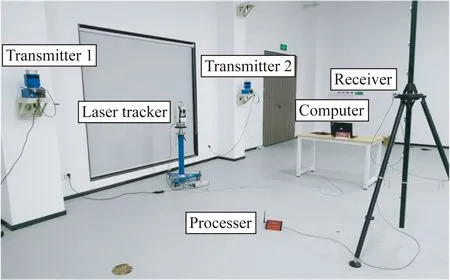
图8 旋转激光测量系统验证实验

Group1：气浮轴承+高分辨率码盘；Group2：机械轴承+高分辨率码盘；Group3：机械轴承+低分辨率码盘。

如图9所示，Group1，Group2结果对比表明，气浮轴承发射站的IRSS和测角精度优于机械轴承发射站；Group2，Group3结果对比表明，高分辨率码盘发射站的IRSS和测角精度优于低分辨率码盘发射站。从折线斜率上看，测角误差的增长速率低于IRSS的增长速率，符合误差分布的实际情况，即测角误差表征包括转速误差在内的整体误差。另外，考虑经脉宽误差补偿后算法仍存在一定的测速误差，IRSS在数值上仍大于实际测角精度。图9中已基本反映出系统的测角精度与IRSS的一致性关系，可利用IRSS对系统测角精度水平进行评价。

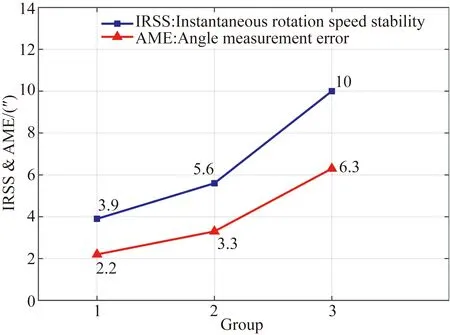
图9 测角精度与瞬时转速稳定度对比

5 结 论

本文建立了旋转激光测量系统的转速误差模型，分析了瞬时转速波动对系统测角误差的影响，引入IRSS作为评价指标，提出了一种瞬时转速算法并分析了算法的分辨率和精度，最后进行了验证实验。结果表明，现有气浮轴承发射站系统的瞬时转速波动测量值从传统算法的±4.5 r/min降至±0.25 r/min，IRSS降至±4″，脉宽误差补偿是提升测速精度的有效方式，系统的测角精度和IRSS存在一致性规律。利用系统的瞬时转速特征，可对系统测角精度进行快速有效的评价。未来在对此类系统的机械旋转模块的机电器件进行性能对比时，可在不引入其他环节误差的情况下，通过解析码盘脉冲计算IRSS以快速评价系统的测角精度水平，为今后电机控制系统、轴系结构等转速相关环节的优化提供了判断依据。