滚齿工艺对热处理畸变的影响研究
2020-12-23王明镜王炯曹荣青束长林樊凡夏三星
王明镜,王炯,曹荣青,束长林,樊凡,夏三星
(南京高速齿轮制造有限公司 制造技术及过程控制处,南京211100)
0 引 言
齿轮渗碳淬火畸变是整个制造过程各个工序畸变的积累,包括设计、锻造、机加工、热处理,而不是由单一某个工序造成的。因而畸变的控制是一个系统的协作过程[1]。
齿轮的热处理畸变同样与前道工序滚齿工艺有一定的关系[2]。滚齿工序在齿坯内部产生加工应力,在齿坯表面引起粗糙度变化,特别是由于滚齿工艺不当、滚齿刀具用钝等因素的影响,会造成更复杂的应力状态。齿轮不同的切齿加工工艺在表层形成不同的加工应力状态,所以其变形倾向也有所不同[3]。
本文采用控制变量法,做三因素两水平正交试验,分别改变滚刀类型、轴向进给、走刀次数,收集热处理各工序前后齿轮的特征尺寸,基于相关统计学原理,分析不同滚齿加工参数对热处理畸变的影响。
1 研究对象、工艺和方法
1.1 研究对象的基本参数
选取的齿轮材料为18CrNiMo7-6,其特点为心部及渗碳层均具有较高的疲劳强度、淬透性、淬火后微畸变和高温使用性能[4]。用光谱仪测定其化学成分,其测试结果如表1所示。

表1 材料18CrNiMo7-6 的化学成分质量分数 %
1.2 研究对象的结构
选取的研究对象为某行星轮,模数为16 mm,其几何外形如图1所示。
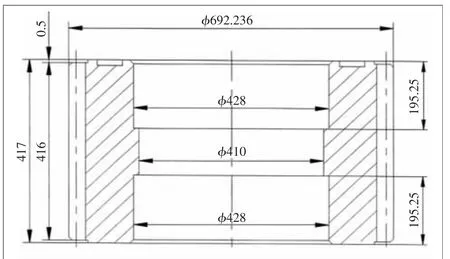
图1 行星轮结构简图
1.3 工艺试验策划
通过三因素两水平正交试验来优化工艺参数,以减小热处理畸变,为减小其他因素干扰,每组试验重复做一次,正交试验策划方案如表2所示。
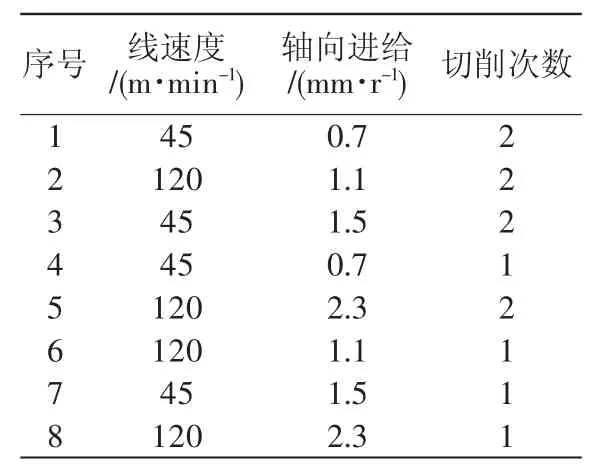
表2 正交试验策划表
1.4 变形的测量方法
实验序号1和8的试验件滚齿、渗碳、淬火后送齿轮计量仪精确测量齿部变形。
选取齿轮的公法线长度、齿顶圆直径及内孔尺寸作为研究齿轮变形的特征对象。测量和计算这些尺寸在渗碳淬火工序前后的变化情况。
齿顶圆直径:对图2中1、2、3、4等4个位置测量基准端、非基准端上下2个位置直径。
内孔直径:对图2中1、2、3、4等4个位置等分测量轴向6个位置内孔尺寸。
公法线长度:对图2中1、4、5等3个位置测量齿宽上、中、下等3个位置公法线。
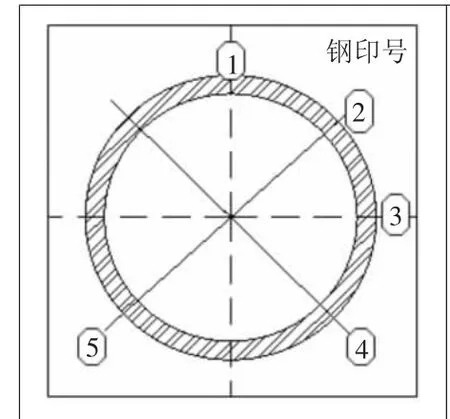
图2 径向测量位置示意图

图3 轴向测量位置示意图
2 热处理宏观变形规律研究
2.1 齿顶圆直径变化规律
分别在滚齿后、渗碳后、淬火后等3个时刻对选定的16个齿轮进行齿顶圆直径值的测量。取同一截面4个位置的均值变化作为变形的衡量依据。齿顶圆尺寸变形数据如表3所示,其变形示意图如图4所示。
由图4可以看出,渗碳后上部齿顶圆缩小,下部齿顶圆变大,齿轮呈锥度变形趋势;淬火相对于渗碳齿顶圆直径有增大趋势,且仍存在一定锥度。
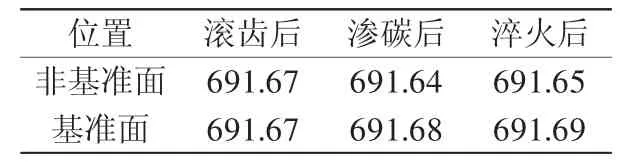
表3 齿顶圆尺寸变形数据 mm
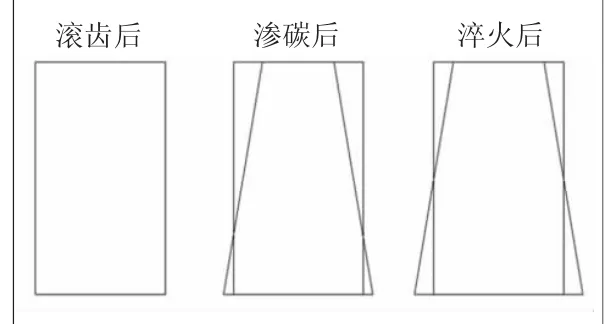
图4 齿顶圆变化示意图
2.2 内孔直径变化规律
分别在滚齿后、渗碳后、淬火后等3个时刻对选定的16个齿轮进行内孔直径测量。取同一截面4个位置的均值变化作为变形的衡量依据。内孔轴向6个位置尺寸变形数据如表4所示,其变形示意图如图5所示。
由图5 可以看出,相对于滚齿后的内孔尺寸,渗碳后的内孔直径呈缩小趋势,且中间部分缩小量最大;相对于渗碳后的内孔尺寸,淬火后的轴向方向靠近两端部位,内孔呈略微增大趋势,但整体仍呈继续缩小趋势,且淬火后的内孔畸变相对于滚齿后的内孔畸变更明显。
2.3 公法线变化规律
分别在滚齿后、渗碳后、淬火后等3个时刻对选定的16个齿轮进行公法线的测量。取同一截面3个位置的均值变化作为变形的衡量依据,且以滚齿公法线数值为0基准进行分析。公法线沿轴向上、中、下3个位置变形数据如表5所示,其变形示意图如图6所示。

表4 内孔尺寸变形数据 mm
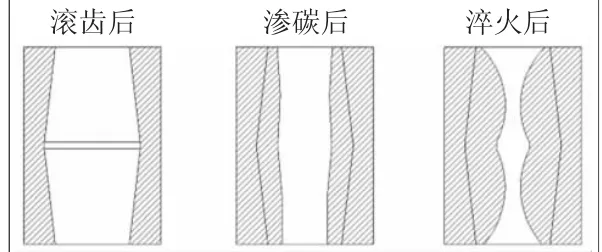
图5 内孔变化示意图

表5 公法线尺寸变形数据 mm
由图6可以看出,与滚齿相比,渗碳后的公法线呈增大趋势,且上部公法线增量最小,下部公法线增量最大,呈均匀锥度变形;与渗碳相比,淬火后的公法线呈缩小趋势,且齿轮上中下各部缩小量不均匀,中部缩小量>上部缩小量>下部缩小量,公法线呈中凹变形。
3 滚齿参数对热畸变相关性研究
3.1 回归方程分析
由第2节研究结果可知,齿轮淬火后中部齿顶圆、内孔尺寸、公法线等特征量畸变明显,故以淬火后公法线缩小量变化作为变形衡量指标,以Minitab为工具研究滚齿工艺参数对热处理畸变影响规律。对齿轮中部淬火后公法线数据(同一截面三等分测量)进行滚齿参数相关性分析,得出标准化效应图,如图7所示。
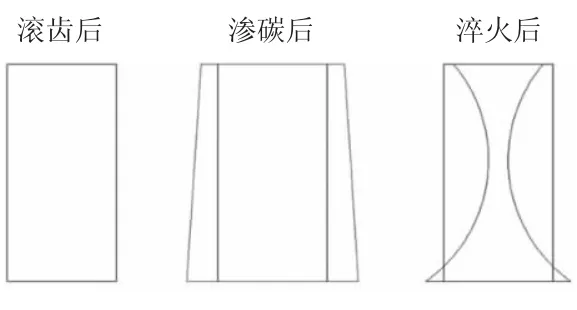
图6 公法线变化示意图
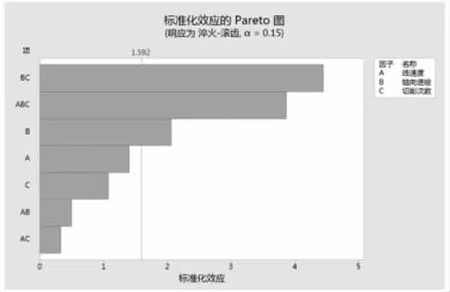
图7 标准化效应柏拉图
由图7可知,轴向进给速度对热处理畸变影响最显著,且线速度、轴向进给速度、走刀次数等3因子交互作用明显。去除误差项精简模型后继续分析,其标准化效应图如图8所示。
由精简模型后的标准化柏拉图和方差分析结果可知,R-sq较大,并且R-sq与R-sq(调整)很接近,故该模型拟合效果很好;建立滚齿工艺参数对热处理畸变的影响模型,对此实验结果拟合的回归方程[5]:Y=-0.08167+0.01042B+0.0225BC+0.01958ABC(淬火-滚齿公法线增量以Y表示)。
3.2 滚齿工艺参数优化
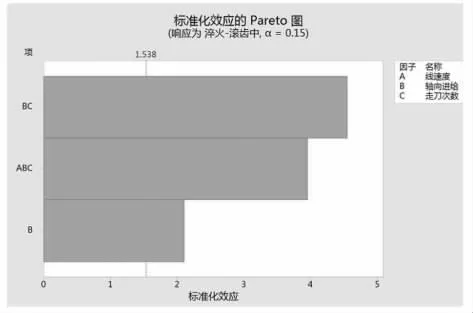
图8 精简模型后标准化效应柏拉图
基于相关统计学原理,为分析不同滚齿加工参数对热处理畸变的影响规律,运用Minitab响应优化器模块来确定滚齿加工最优工艺条件。
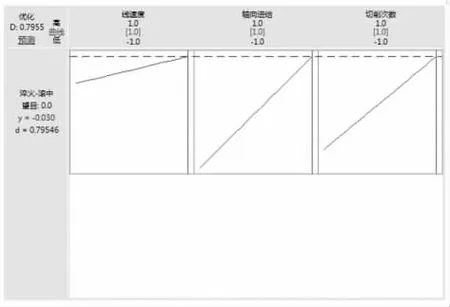
图9 淬火-滚齿公法线增量响应优化图
由响应优化图可知,当线速度、轴向进给速度、切削次数均取高水平工艺参数时,淬火相对滚齿的热处理畸变最小,优化符合合意性达79.55%。
同理,可拟合出渗碳-滚齿、淬火-渗碳、淬火-滚齿各阶段公法线变动量与滚齿工艺参数之间的回归方程,并计算出高、低水平滚齿工艺参数时各阶段公法线变动量,如表6所示。
从表6中可以看出,高水平滚齿工艺参数时,渗碳后、淬火后公法线变动量相对较大,但两者之间存在相互抵消作用,即机械加工产生的残余应力与热处理产生的热应力、组织应力相互平衡抵消作用,使最终热处理状态淬火-滚齿公法线畸变量最小为-0.02971,远小于低水平时公法线变动量。即当线速度、轴向进给速度,切削次数均取高水平时,综合畸变量最小。
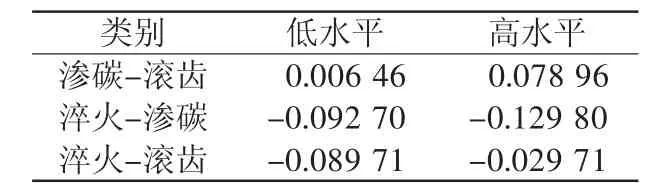
表6 高、低水平滚齿参数公法线变动数据表 mm
4 结 语
通过改变滚齿工艺参数,作三因素两水平正交试验,探究滚齿工艺对热处理畸变的影响,研究结果如下:1)选取某行星轮作为试验对象,采用控制变量法,分别改变线速度、轴向进给、走刀次数,收集热处理各工序前后齿轮的齿顶圆直径、内孔尺寸、公法线数据,分析出齿轮热处理宏观变形规律;2)基于Minitab统计分析工具分析不同滚齿加工参数对热处理畸变的影响规律,确定滚齿加工最优工艺条件;当滚齿线速度、轴向进给、切削次数均取高水平参数时,热处理综合畸变最小,得出符合加工条件的最佳切削参数。
本文只统计分析了行星轮的热处理变形数据,以后可尽量多地统计不同类型齿轮的热处理变形数据,基于大数据的思想,得到更准确、全面的热处理畸变规律,以指导现有工艺改进和现场生产工作。获得该类型齿轮热处理畸变规律后,可优化留磨滚刀的设计与应用,在热处理前合理调整齿轮切深和留磨量,以补偿公法线变动,提高磨齿质量[6]。
