扩展A*算法的火灾逃生路径规划研究*

程鹏举，吴 楠，孟凡坤，李 爽

（1.中国人民解放军战略支援部队信息工程大学，河南 郑州 450000；2.郑州大学，河南 郑州 450000）

0 引言

随着现代城市规模的不断扩大，大型场馆和高层建筑越来越多，且楼层高，结构复杂，人员密集。现有的消防疏散逃生设备不能根据火灾实际情况进行相应的改变，可能会导致逃生人员跑向火情点。因此，当发生火灾时，如何智能规划出有效的逃生路径对人员进行安全指引，降低火灾中人员的伤亡代价是十分有价值的研究[1]。而如何有效引导人员进行疏散逃生涉及到路径规划问题，故本文重点研究路径规划算法。

目前，有大量的专家学者在路径规划领域做了较多研究，包括人工势场法、A*算法、蚁群算法及粒子群算法等[2]。其中，A*算法具有计算量小、规划路径快等特点，但算法的启发函数考虑维度较简单，规划出的路径容易冗余。文献[3]在传统的八角度搜索邻域基础上，设计了多角度A*算法，可获得更短的可行路径。文献[4]通过目标性扩展、目标可见性判断、改变启发函数以及改变扩展节点选取方略等4 个方面改进A*算法，使算法运行得更快。文献[5]将A*算法扩展到24 邻域，使路径方向具有更多选择，并融合曼哈顿距离和欧几里得距离，提高算法的路径规划能力。文献[6]针对多U 型障碍环境，引入邻域矩阵进行障碍搜索以提升路径安全性，结合角度信息和分区自适应距离信息改进启发函数以提高计算效率。以上研究对A*算法的改进提高了算法效率，但都没有讨论算法在某位置存在多个最小代价因固定选取第一个最小代价值而造成路径曲折的情况。针对此问题，本文提出扩展A*算法。当传统A*算法在某点处出现多个最小代价值时，假设每个最小值点为下一点，依次对其进行扩展计算，直到找到最小综合代价值，并选择此分支为最优路径。

1 环境建模与算法原理

1.1 环境建模

本文简化建筑物模型，假设各楼层之间的消防楼梯安全且仅通过此处相互连接，并采用栅格法对各个楼层的环境进行建模[7]。将各楼层二维平面划分为N×N的地图，Ni={1,2,3,…,N2}。按照从左至右、从下至上依次编排，分为自由栅格、障碍栅格和火情栅格3 种栅格，人员只能在自由栅格中跑动，模型如图1所示。栅格图中，可通行区域设为自由栅格，障碍区域设为障碍栅格，发生火灾的区域设为火情栅格，障碍物和火情不足1 格的区域按照1 个栅格计算。

每个栅格中心坐标可表示为：

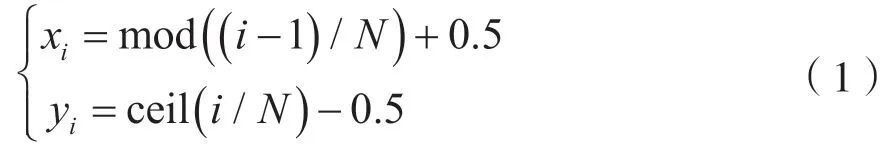
式中，mod 为求余运算，ceil 表示向后取整数。

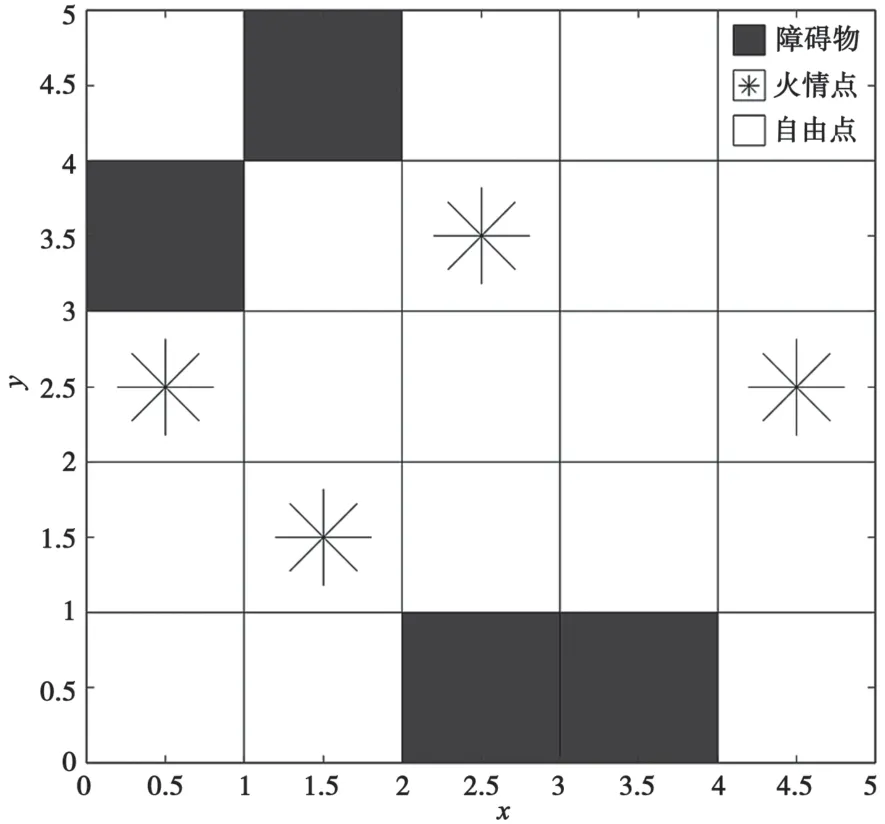
图1 环境栅格示意

本文忽略人流密度、人员情绪以及烟雾浓度等影响，并假设人员的平均逃生速度为单位速度，其在逃生时的运动模型如图2 所示，即人员每次只能向相邻的8 个栅格内移动1 格。

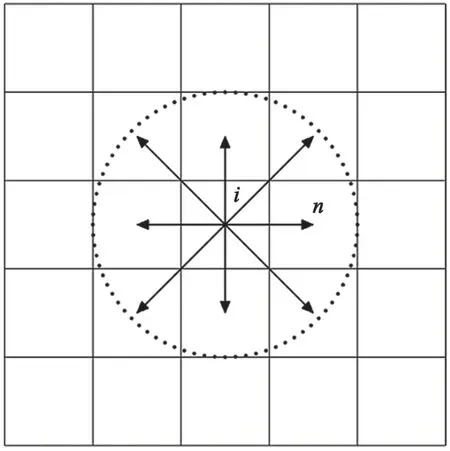
图2 运动邻域模型

1.2 A＊算法原理

A*算法通过对相邻8 个节点计算代价值，在进行启发式搜索提高效率的同时，可以找到一条优化路径[8]。算法从起点T开始，依次对8 邻域可通行节点计算启发代价值，直到找到终点S或进入死胡同或遍历完所有自由节点[9]。

算法的启发函数为：

式中：g(n)是从起始点T到节点n的实际代价；h(n)是从节点n到终止点S的估计代价；f(n)为节点n的代价函数[10]。

式中：Li是起始点T到当前点i的实际代价且初始值为0；xn、yn、xi、yi、xS、yS分别为节点n、当前点i和终点S的横纵坐标值[11]。设立集合close用于存储已经走过的节点，使其不被再次搜索。算法流程如图3 所示。

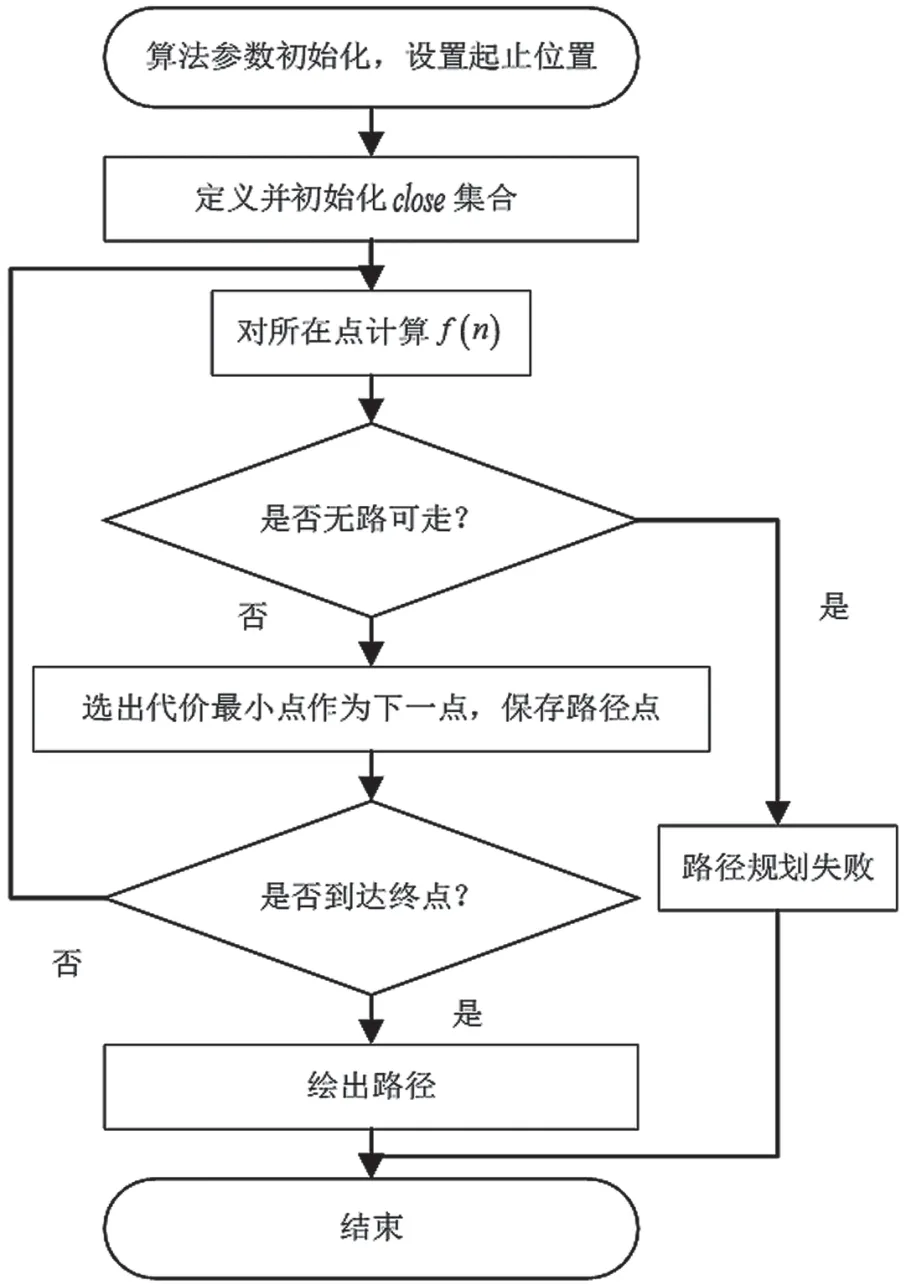
图3 A*算法流程

2 扩展A＊算法

传统的A*算法在一定情况下会陷入多个最小代价值的困境，在选取下一点时往往选择位置靠前的最小代价，不能对多个最小代价值的路径进行评估后选择最佳路径。其中，算法在特定情况出现两个最小代价点的示意图如图4 所示。图中T、S为起止点，在点i处，其可选下一点为图中点{1,2,3,4}的位置，其中最小代价点有{3,4}两点，算法默认选择靠前的最小代价即点3，规划出的路径为A 路径。相比之下，另一最小代价点即点4，其规划出的B 路径转折少，路径更短。由此看出，当环境规模较大时，一旦陷入此困境，将使规划出的路径曲折往复，大大增加了路径长度。在火灾逃生路径规划中，曲折的路径和较长的路线将大幅增加人员逃生耗时，降低逃生效率。

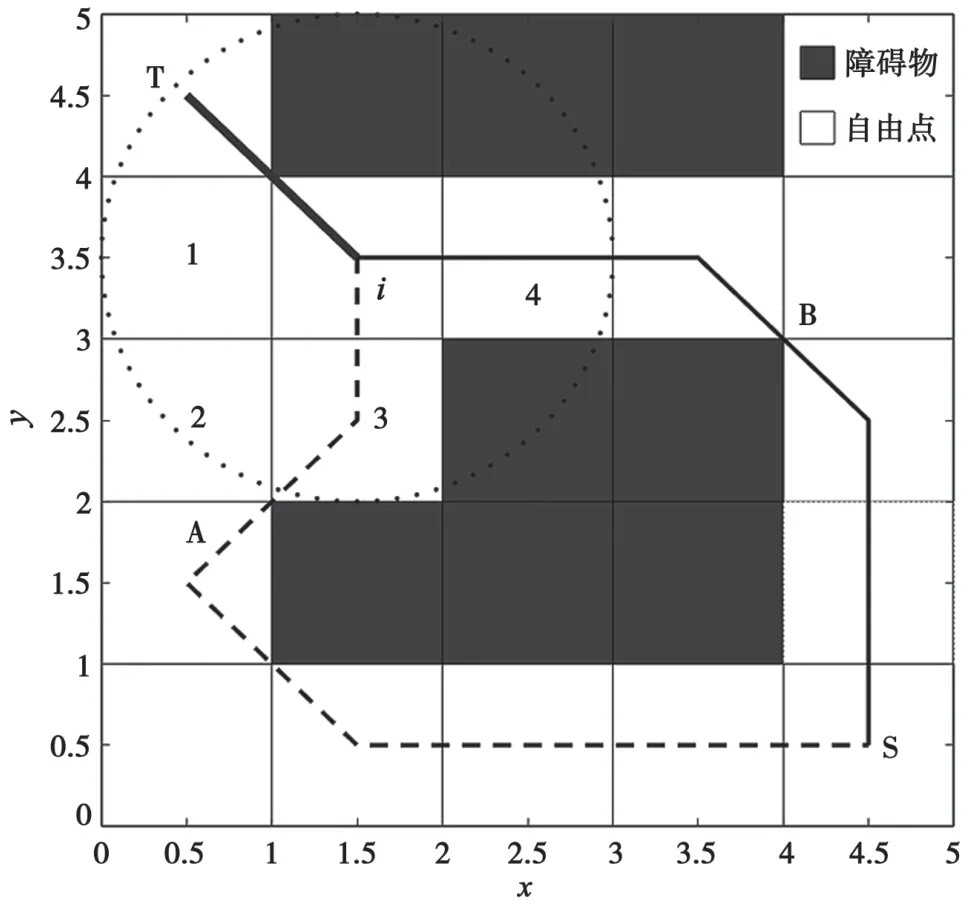
图4 两最小代价点情况

本文针对此困境提出扩展A*算法，在其出现多个最小代价值时依次扩展每个最小值。假设每个最小值点为其下一点，并计算该点邻域的启发代价，将得到的最小代价值累加到上一层的代价中，对比其综合代价，选择综合代价最小的路径。当扩展层最小代价值也相等时，再以此为基础扩展其下一层，计算其最小代价值，累计到上一层。依次类推，直到最后选择综合代价最小的分支。改进后的算法流程如图5 所示。

3 仿真验证

为验证改进后算法的有效性，本文的实验平台如下：计算机CPU 为Inter Core i7-8750H（2.2 GHz），内存为8 GB，显卡为NVIDIA GeForce GTX1050Ti，仿真软件为MATLAB R2018b。A*算法的启发距离为欧几里得距离。

在30×30 的环境地图中，对传统A*算法和扩展A*算法进行10 次仿真实验，结果如表1 所示。表1 中，l1、l2分别表示传统A*算法和改进后的扩展A*算法规划出的路径长度。虽然扩展A*算法在多个最小代价点需要对每个最小值进行扩展计算，增加了计算量，但可以选择最佳路径，使路线变短，减少需要计算的路径点。两者相互抵消后，从表1的计算时间均值可以看出，两种算法的计算量相差不大。

图5 扩展A*算法流程

表1 传统A＊算法和扩展A＊算法结果比较

从图6 和图7 可以看出，算法在圆圈标记的位置出现两个最小代价点。传统的A*算法选择靠前的最小代价，导致规划出的路径长且曲折。改进后的扩展A*算法在扩展一层后，其最小代价值依然相等；当经过两层扩展后，最小代价值不同，最后选择出综合代价最小的路径，规划出的路径平滑且大幅缩短了长度。综合以上结果分析可知，在此环境下，两种算法的计算时间相差不大，但改进后的扩展A*算法规划出的路径缩短了50.7279，降幅约52%，且路线远离火灾区域，更便于人员逃生。实验表明，改进后的A*算法在多最小代价值位置可以选择最优分支，可高效地进行路径规划。

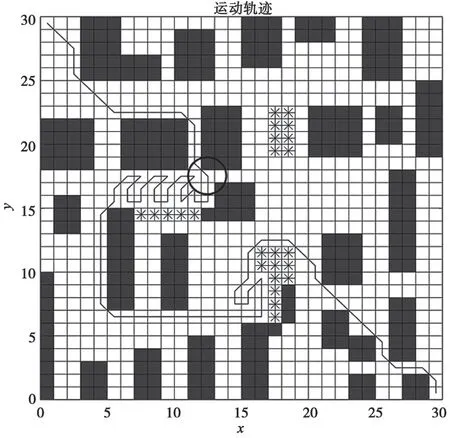
图6 传统A*算法结果

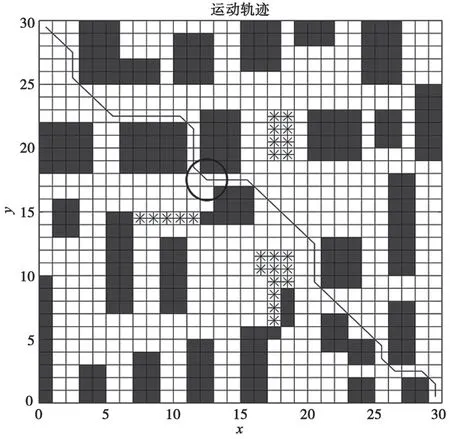
图7 扩展A*算法结果

4 结语

发生火灾时，结合路径规划算法的智能逃生指引可大大降低火灾中人员伤亡程度。传统的A*算法计算速度快，但在多最小代价点处固定选取第一个最小代价值容易规划出较长路径，不利于人员逃生。针对此问题，本文提出扩展A*算法，在多最小代价点处对每一个最小代价进行扩展计算，并将扩展后的最小代价累加到上一层，以此类推，直到选择出综合代价最小的分支，从而使改进算法规划出的路径更短。在MATLAB 软件中对其进行仿真验证，结果表明，改进后的扩展A*算法规划出的路径更短，算法寻优效率更高，应用在火灾逃生中可大大提高逃生效率，降低人员伤亡。