基于PGM 的态势预测技术*

刘俊波，黄 斌，邓 蕾

(中国电子科技集团公司第三十研究所，四川 成都 610041)

0 引言

机器学习[1]是现阶段实现人工智能应用的主要方法。机器学习最重要的任务是根据已观察到的数据对感兴趣的未知数据进行估计或推测。

概率模型（probabilistic model）提供了一种描述框架，将学习任务归结于计算变量的概率分布，即如何基于已知变量推测出未知变量的条件分布。

概率图模型[2][3]（probabilistic graphical model）是一类用图来表达变量相关关系的概率模型。概率图模型大致可分为两类：第一类是使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网；第二类是使用无向图表示变量间的相互关系，称为无向图模型或马尔可夫网[4]。

隐马尔可夫模型[5]（Hidden Markov Model，简称HMM）是结构最简单的动态贝叶斯网，它是一种著名的有向图模型。

本文基于HMM 采用两种方法实现系统的态势预测。这两种方法在不同的场景中预测效果良好。

1 隐马尔可夫模型（HMM）

隐马尔可夫模型可以计算出一个系统每一时刻处于各种状态的概率以及这些状态之间的转移概率。

系统有n种互斥的状态（状态1，状态2，状态3，…），即系统的状态可以构成集合

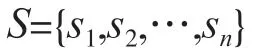
设在t时刻系统的状态为zt，它是一个离散型随机变量。从时刻1 开始到时刻T为止，系统所有时刻的状态值构成一个随机变量序列：

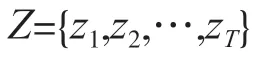
系统在不同时刻可以处于同一种状态，但在任何一个时刻，系统只能有一种状态。不同时刻的状态之间是有关系的。时刻t的状态由它之前时刻的状态决定，这可以表示为如下的条件概率：

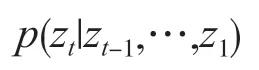
即在从1 到t-1 时刻系统的状态值分别为z1,z2,…,zt-1的前提下，时刻t系统的状态为zt的概率。如果要考虑之前所有的状态，数学模型太复杂。因此，可以做一个简化，假设t时刻系统的状态只与t-1时刻系统的状态有关，与更早的时刻无关。上面的概率可简化为

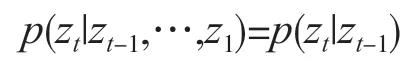
系统状态的取值有n种可能，在t时刻取任何一个值与t-1 时刻取任何一个值的条件概率构成一个n×n的矩阵A，称为状态转移概率矩阵，其元素为

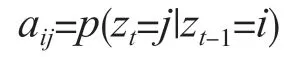
这个矩阵的元素表示t-1 时刻系统的状态为i，t时刻系统的状态为j的概率，即从状态i转移到状态j的概率。如果知道了每一时刻的状态转移矩阵，就可以计算出任意时刻系统状态取每个值的概率。状态转移矩阵的值通过训练样本学习。

状态转移概率矩阵的元素必须满足如下约束：

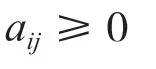
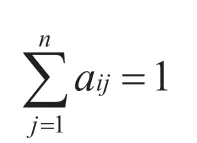
第一条是因为概率的值必须为[0,1]，第二条是因为无论t时刻的状态值是什么，在下一个时刻一定会转向n个状态中的一个，因此，它们的转移概率和为1。另外，还需要为系统指定初始状态z0=s0。

由该模型产生一个状态序列z1,z2,…,zT的概率为

结果就是状态转移矩阵的元素乘积。在这里，假设任何一个时刻的状态转移矩阵都是相同的，即状态转移矩阵与时间无关。

状态转移矩阵通过训练样本学习得到，训练时的损失函数使用对数似然函数。给定一个状态序列z，定义马尔可夫过程的对数似然函数为

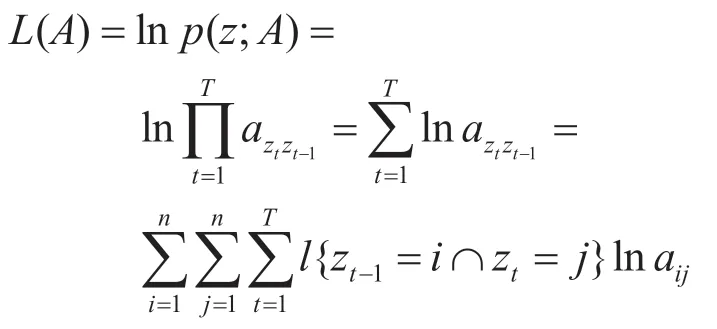
因为状态转移矩阵要满足上面的两条约束，因此，要求解的是如下带约束的最优化问题：

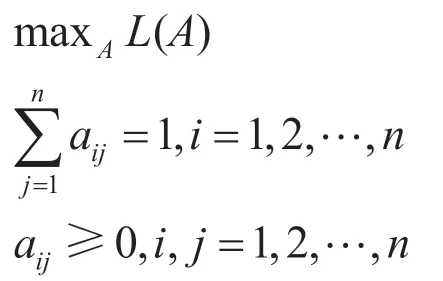
由于对数函数的定义域要求自变量大于0，所以可以去掉不等式约束，上面的最优化问题是一个带等式约束的优化问题，可以用拉格朗日乘数法求解。构造拉格朗日函数：

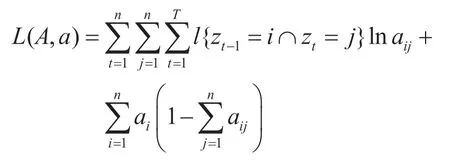
对aij求偏导数并令导数为0，可以得到

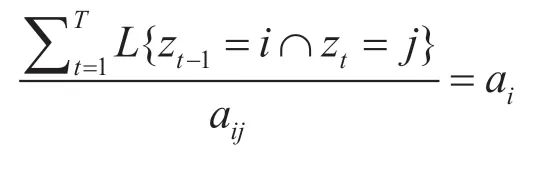
解得

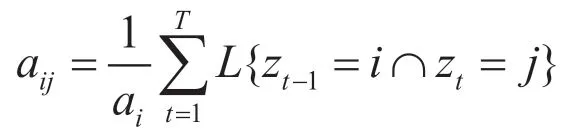
对ai求偏导数并令导数为0，可以得到

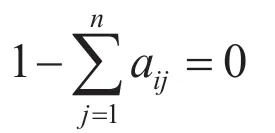
将aij带入上式可以得到

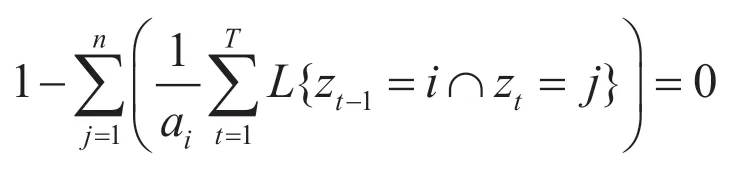
解得

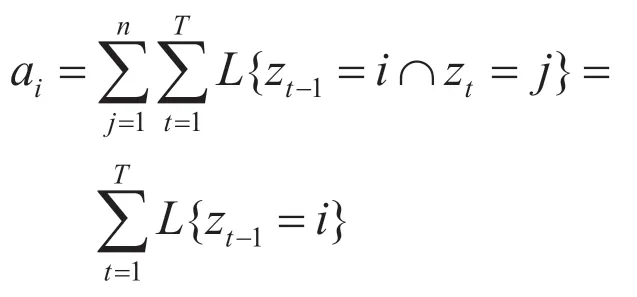
合并后得到下面的结果：

也就是说，从状态i转移到状态j的概率估计值，就是在训练样本中从状态i转移到状态j的次数除以从状态i转移到下一个状态的总次数。

2 实验方案

实验的核心技术思想为采用PGM 算法对系统的历史状态数据即训练样本进行学习，求出状态转移矩阵，从而对系统的未来状态进行预测。

实验分为三个阶段：

（1）样本预处理。一个系统包含多个子系统。子系统的状态有四种，分别记为状态1、状态2、状态3、状态4。分别查询每个时刻（间隔1 小时或间隔固定时长）各个子系统的状态，并统计整个系统各个时刻、各个状态的总数量。

（2）计算状态转移矩阵。根据预处理结果，取前80%的数据作为样本集，统计各个状态转移次数，求出各个状态转移概率，得到状态转移矩阵。

（3）预测。取欲处理结果的后20%作为测试集，根据状态转移矩阵，计算未来某一时刻系统的各个状态的数量。

3 实验结果

本文给出两种预测方法。其中，状态转移矩阵的选取不同。

第一种，状态转移矩阵不随时间变化。分别统计出各个状态在各个时刻的预测数量和实际数量。实验结果如表1 和图1 所示。

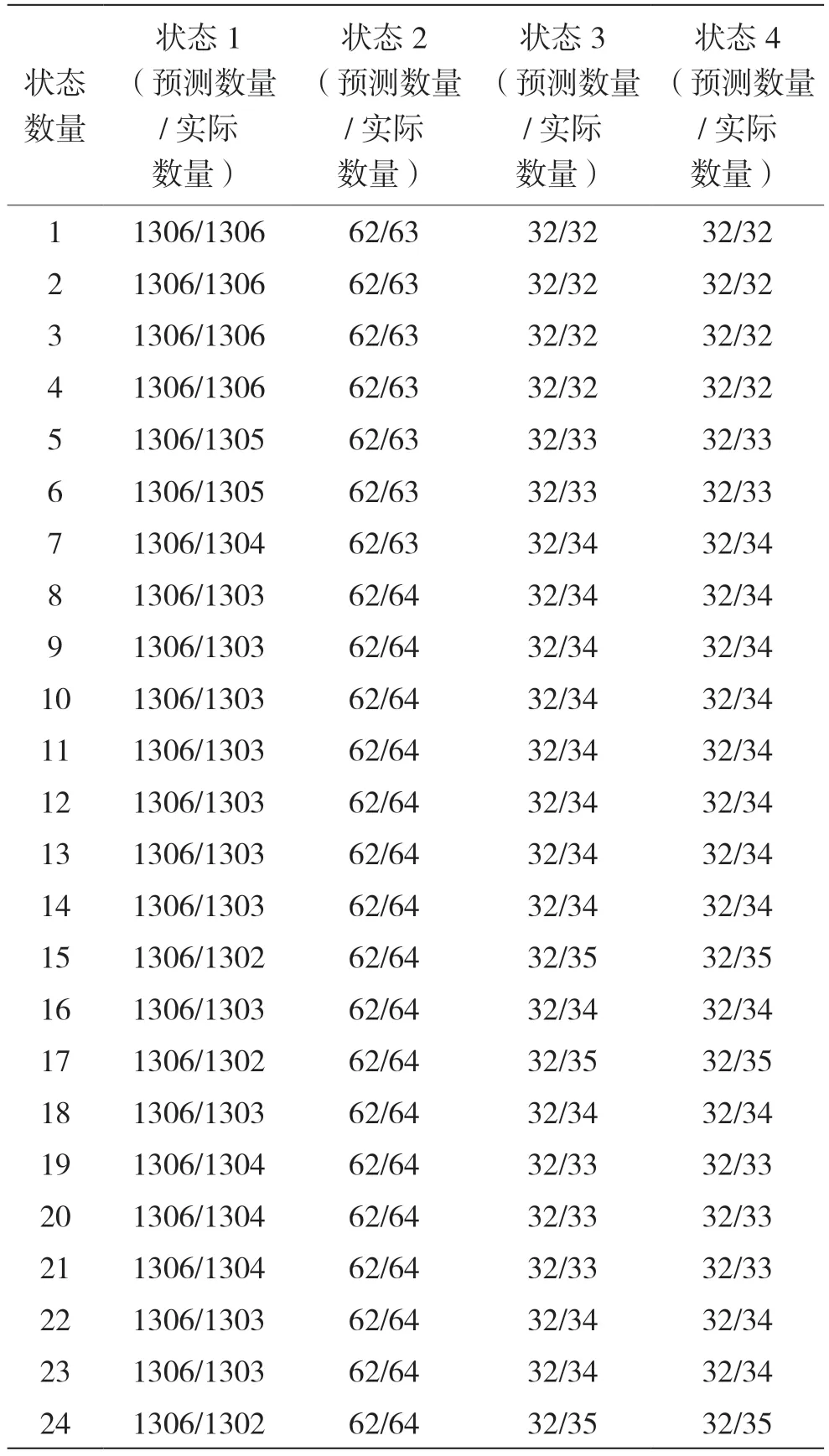
表1 第一种方法结果

其中，四张图分别表示各个状态的预测数量和实际数量的对比图，蓝色线表示预测结果，红色线表示实际结果。

第二种，状态转移矩阵随时间变化。状态转移矩阵每时刻修正一次，且采用贝叶斯权重模拟计算状态转移概率，即系统当前的状态和它前一时刻的状态相关性最大，往前依次根据贝叶斯系数递减。贝叶斯函数为

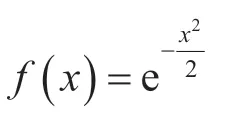
贝叶斯函数图像如图2 所示。

实验结果如表2 和图3 所示。

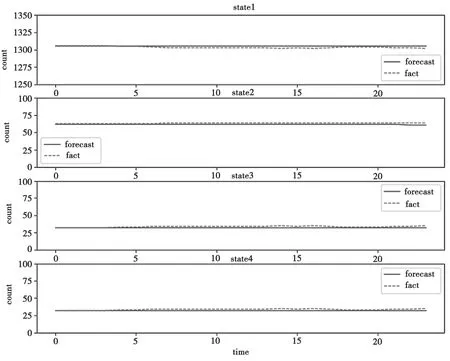
图1 方法一结果

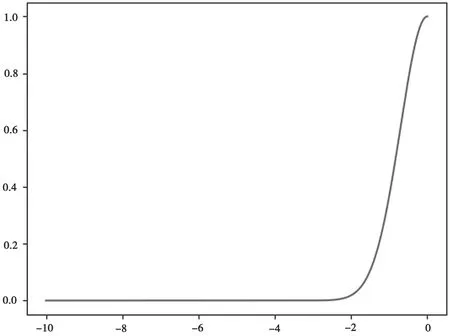
图2 贝叶斯函数

第一种方法，只能预测前几个时刻，随着时间推移，预测效果不理想，但是由于状态转移矩阵固定，所以该方法计算量小。第二种方法，由于状态转移矩阵随时间不断变化，计算量有所增加，但可以较好地预测未来任意时刻系统的状态。

4 结语

本文基于PGM 算法，给出了两种预测系统状态的方法。第一种方法可以快速预测未来前几个时刻的状态，具有计算量小的优点；第二种方法，通过不断调整状态转移矩阵，虽然增加了计算量，但可以预测未来任意时刻系统的状态。这两种方法与神经网络方法预测相比，具有计算量小的优点，均具有可行性。