基于扩展Lanchester方程的非对称型海战效能研究*

（91404部队 秦皇岛 066001）

1 引言

传统意义的Lanchester模型主要通过建立敌我平台耗损的微分方程组的形式［1～3］来比拟该作战进程，但使用该模型来描述非对称型海战存在两个缺点，一是在非对称型海战中，优势一方先敌发现，率先攻击，使得敌我双方平台耗损过程呈现很大差异；二是当代海战具有进程快、平台兵力耗损的“跳跃”性、“间断”性等特点［4～7］，难以确定非对称型海战何时进行平台补充，因此需要研究扩展的Lanchester模型。

2 传统Lanchester方程

传统的Lanchester方程通常用三个通用性的方程来描述［8～10］，即Lanchester方程第一线性率方程、第二线性率方程以及平方率方程。

假设a、b分别代表蓝、红两军平台在单位时间内对敌对方平台的平均毁伤威力数，x、y为任意t时刻敌我两军平台的剩余数量的平均数，x0、y0为敌我两军平台开始时刻的平台数。Lanchester第一线性率方程、第二线性率方程和平方率方程可描述为［11～12］

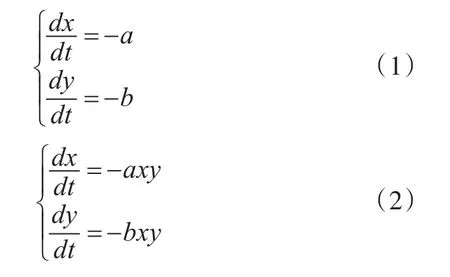
3 扩展Lanchester模型

非对称型海战可以划分为两个阶段。第一阶段是优势的部队可以精确探测到敌方目标方位距离等信息，而弱势一方只能估计到某个海域的海战，定义为“可见-不可见”阶段；第二阶段是敌我两军同等可精确探测到对方平台的海战，及“可见”阶段。

3.1 “可见-不可见”阶段

假设蓝军为性能优势一方，红军为弱势的一方，其中a、b分别为蓝红两军于单位时间内单发炮弹对红蓝两军平台的平均毁伤威力（其中b此时为0）；x（n）、y（n）为在n时刻红蓝两军平台数量，x0、y0为红蓝两军开始平台数，c（n）、d（n）分别为红蓝两军在n时刻的支援平台［1］。

那么此时红蓝两军战斗模型为

通过迭代可求的：

求解上式可得：

如下结论：

1）“可见-不可见”阶段不存在和局条件，随着战斗次数的增多，红方即弱势一方的耗损越来越多，说明弱势一方在遭受不对等作战时，要尽快探明敌情，尽早发现敌方。

2）该阶段红方（弱势一方）为避免快速落败，应该加大平台补充力度。

3）该阶段蓝方（优势一方）的耗损与己方开始平台无关，性能优势一方，投入较少平台就可取得战斗胜利，证明了舰艇隐身性和预警探测性能对于战局决定性影响。

3.2 “可见”阶段

随着战斗的进行，敌我两军终将可精确探测到对方的海战，进入“可见”阶段。“可见”阶段海战模型类似于Lanchester平方律模型［1］。

此时红蓝两军战斗模型为

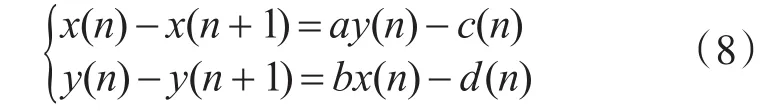
求解式（11）比较困难的，可以考虑某一小段时间，假设只有n+1点，两军有平台增援，此时有：

当i≤n时；求解式（11）可得：

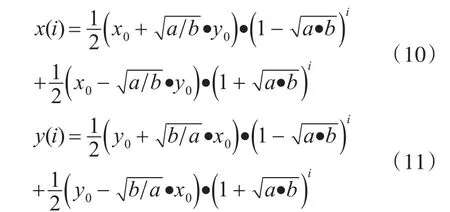
当i≥n+1时，求解式（11）可得：

其中：x0、y0分别为进入“可见”阶段时的红蓝两军开始平台：

结合以上公式可得：

红蓝双军平台数量的损失与我方开始平台数量有关，我军开始平台越多，越容易获得战争的胜利。

红蓝双军平台数量的变化与敌对两军单发炮弹的平均毁伤威力有关，我军对敌方炮弹杀伤性越大，越容易获得战争的胜利；而且存在时，即时，红军平台的耗损小于蓝军的耗损，此条件下类似于Lanchester平方律方程。

3.3 非对称型海战和局条件

非对称型海战模型分为两个阶段，第一个阶段不存在和局条件，弱势一方由于无法观察敌方，只能被动挨打，直至进入第二阶段，此时时刻为T，想要达到和局，无支援兵力条件下必须满足如下条件：

同时在第一阶段中：

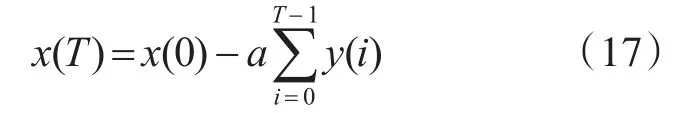
以此可得非对称型海战和局条件：

4 仿真实例

前文已经推导出非对称型海战的解析解，得到的平台耗损和单发炮弹的平均毁伤威力和平台数量的关系并不直观可见，同时平台补充的数量和时机的关系不易得到，因此需要仿真验证，其中弱势一方从时间2开始观察到目标，及从“可见-不可见”阶段进入“可见”阶段。

模型一：在无平台补充条件下

1）红蓝两军开始平台相同，单发弹毁伤威力不同，即 x0=y0=20，a=0.1，b=0.05；此时红蓝两军平台耗损如图1所示。

图1 开始平台相同、单弹毁伤威力不同战斗

2）红蓝两军开始平台数量不同，单发弹毁伤威力不同，即x0=20，y0=32，a=0.1，b=0.05；同时开始平台满足式（21）和局条件，因此战斗结果为和局，此时红蓝两军平台耗损如图2所示。

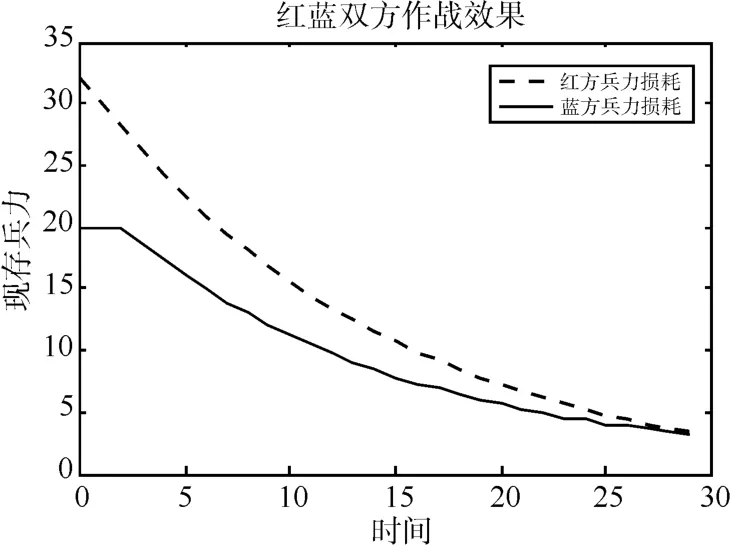
图2 和局条件下的战斗

从该模型可以得到：单发炮弹的平均毁伤威力和平台数量影响战局，在“可见-不可见”阶段，是弱势一方单方面耗损过程，因此在非对称型海战中，弱势一方取得胜利，需投入大量平台。

模型二：有平台补充条件下

1）红蓝两军开始平台相同，单发弹毁伤威力不同，即x0=y0=20，a=0.1，b=0.05；红方平台在i=1时刻（及第一阶段时刻内）支援为7，蓝方无支援，满足非对称的海战和局条件，此时红蓝两军平台耗损如图3所示。

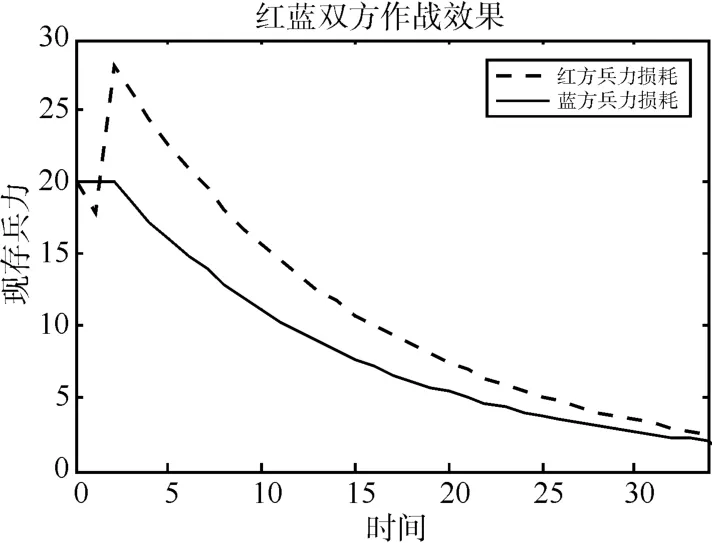
图3 红方有平台补充条件下的作战（i=1，c=7）

2）红蓝两军开始平台相同，单发弹毁伤威力不同，即x0=y0=20，a=0.1，b=0.05；红方平台在i=5时刻（及第二阶段时刻内）支援为10，蓝方无支援，满足非对称型海战和局条件，此时红蓝两军平台耗损如图4所示。

图4 红方有平台补充条件下的作战（i=5，c=10）

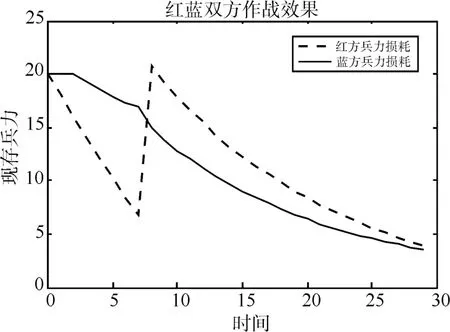
图5 红方有平台补充条件下的作战（i=7，c=11）

3）红蓝两军开始平台相同，单发弹毁伤威力不同，即x0=y0=20，a=0.1，b=0.05；蓝方平台在i=7时刻（及第二阶段时刻内）支援11；蓝方无支援，为非对称的海战和局条件，此时红蓝两军平台耗损如图5所示。

结合图5可得如表1。

表1 和局条件汇总表

从该模型可以得到：在非对称型海战中，平台兵力的补充可以有效改变战局变化，单发炮弹毁伤威力小和隐身性能差的弱势一方当其支援数大于平衡条件数，即满足和局条件就可改变战局胜负；同时由表1可得，弱势一方想最小代价扭转败事，需要在发现目标后尽早支援，而在未发现目标情况下支援，对于战局影响不大。

5 结语

本文根据现代非对称型海战的特点，提出了扩展Lanchester模型，推导了非对称型海战的两阶段的数学表达式以及和局条件，应用仿真手段进行了验证研究，本文的结果对我海军对于强敌作战有一定借鉴意义。但论文存在一定不足，其一是未考虑双方平台补充可能导致舰艇编队整体探测能力增加，其二是未考虑平台作战中队形和战术对于海战的影响，需要下一步研究。