中外小学高年级数学竞赛试题难度的比较研究——以“华杯赛”与“袋鼠赛”为例
2020-12-22蒋培杰
蒋培杰,张 勇,熊 斌
中外小学高年级数学竞赛试题难度的比较研究——以“华杯赛”与“袋鼠赛”为例
蒋培杰1,2,张 勇1,2,熊 斌1,2
(1.华东师范大学 数学科学学院,上海 200241;2.上海市核心数学与实践重点实验室,上海 200241)
小学数学竞赛试题的难度与数学的普及和竞赛活动本身的社会反响密切相关.对当前国内外小学数学竞赛试题的难度进行探讨,回答了国内小学数学竞赛与国外相比是否太难的问题.首先在已有模型的基础上构建小学数学竞赛试题综合难度的一个多因素模型,对中外两类参与面很广的小学高年级数学竞赛“华杯赛”和“袋鼠赛”近6年的试题进行综合难度比较,利用SPSS22处理所得数据.在考虑到中外国情、文化传统差异的基础上得到如下结论:国内小学数学竞赛试题的难度较高,应适当降低难度;国内小学数学竞赛应进一步处理好普及与提高的关系;国内小学数学竞赛试题在情境上应更加生活化,在认知上应更贴近学生的思维水平.
袋鼠数学;华杯赛;难度;小学数学竞赛
华杯赛始于1986年,是一项纪念中国著名数学家华罗庚(传承其精神)的全国性少年数学竞赛活动,竞赛命题的基本原则是:普及性、趣味性和新颖性[1].普及数学是该竞赛的重要目的和根本出发点.国际上以普及数学和最基本的数学文化为宗旨的小学数学竞赛参与面较广的是袋鼠数学竞赛(Math Kangaroo),该竞赛(以下简称袋鼠赛)始于1991年,目前全球每年有超过600万中小学生参与该赛事.该活动在美国、法国和加拿大等国家受到孩子们及其家长的一致欢迎和好评[2].恰与之相反,华杯赛等小学数学竞赛在中国已经被明令禁止开展.同样以普及数学为宗旨的数学竞赛活动,为什么会有如此不同的结局?很明显,袋鼠赛在国际上日渐受欢迎,在数学普及上,袋鼠赛日益展现它的价值;而华杯赛等活动在数学普及上已然无力,因为活动本身已经被禁停.其中的原因非常复杂,但不少人持这样一种观点:小学数学竞赛的内容超出了孩子们的认知水平,过难的试题不仅没有激发孩子们的兴趣,反而是对孩子们的摧残[3].国内小学数学竞赛的试题是否真的太难?考虑到小学高年级是小学生思维发展的关键时期,为了解中外小学数学竞赛活动的差异,弄清楚国内小学数学竞赛试题是否过难,以华杯赛和袋鼠赛为例,比较它们小学高年级数学竞赛试题的综合难度能够得到一些启示.
1 小学数学竞赛试题的综合难度模型
数学试题的难度指的是数学试题的难易程度,单个试题的难易程度可以用难度系数来刻画,难度系数越低,通过的人越少,试题越难.经典测量理论(CTT)难度系数在数值上反映的是考生群体在该试题上的通过率或得分率;项目反应理论(IRT)中,难度被定义为试题本身固有的特性,不随考生样本的变化而变化[4].由于数学课程难度的国际比较和大规模高利害数学教育考试命题等实际需要,要对试题本身固有的难度进行量化,因此发展出很多试题绝对难度的估计模型.比如,考虑影响数学试题难度的信息量、思维水平、推理步骤和认知要求等各因素而设计的综合难度模型[5].模糊综合评判和神经网络等方法也用于试题客观难度的刻画[6-7].国外有研究者将影响数学试题难度的因素进行了梳理,影响因素主要有情境、原理和知识技能等17个[8].目前,综合难度模型多用于数学课程难度的跨国比较[9-13],在考试方面涉及高考试题的综合难度模型已经有研究[14].基于已有的综合难度模型,考虑小学数学竞赛的特点,在专家论证的基础上,确定符合小学生特点的难度影响因素结构及各水平的权重,构建小学数学竞赛试题的五因素综合难度模型分析框架(见表1),用该框架作中外小学高年级数学竞赛试题综合难度的分析比较.
以下给出两个按照上述框架进行因素水平分析的具体例子.
例1 设是一个平方数,如果-2和+2都是质数,就称为型平方数,例如,9就是一个型平方数,那么小于1 000的最大型平方数是.(2016年华杯赛小高组初赛第9题)
该题主要考查同余的思想,试题情境为数学本身,信息量为知识较多,运算次数为多次运算,推理类型为复杂推理,认知要求为分析水平.
例2 What is the greatest number N, which, when divided by 7, has a remainder that is equal to the quotient?(2014年袋鼠赛五~六年级第20题)
(A)7 (B)8 (C)48 (D)56 (E)77
该题译为:被7除所得的商和余数相等的最大的整数是多少?
该题主要考查带余除法,试题情境为数学本身,信息量为知识较多,运算次数为简单运算,推理类型为简单推理,认知要求为理解水平.

表1 小学数学竞赛试题综合难度模型分析框架
基于已有模型[9-14],按表1所示框架,单个因素的难度模型为:
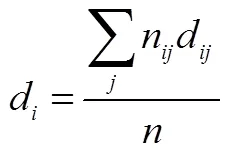
综合难度模型为:
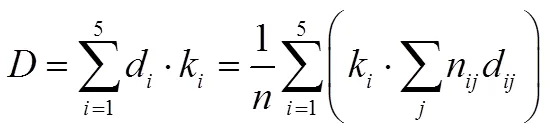
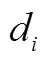
2 中外小学高年级数学竞赛试题难度的比较
选取华杯赛小学高年级组初赛(以下均简称为华杯赛)和袋鼠赛五~六年级(以下均简称为袋鼠赛)近6年的试题进行分析.这两类竞赛的考生均处于小学高年级阶段(五年级和六年级),两类竞赛的本质目的都是普及数学.其中,华杯赛是国内参与人数最多的小学数学竞赛之一;袋鼠赛则是国际上参与人数最多的国际性小学数学竞赛.华杯赛一般是6道选择题,4道填空题,答题时间为60分钟;袋鼠赛是30道选择题,答题时间为75分钟.两类竞赛试题除了考查小学阶段基础的数和几何知识外,都或多或少涉及到初等数论和组合数学等离散数学的内容.相对而言,华杯赛更注重数学的深度,数学味道较浓,如2018年的第5题,从1—20这20个整数中任选11个,要回答必有两个整数的和是21.该题考查的是抽屉原理,要能正确构造“抽屉”才能完成解答.袋鼠赛则更注重数学与生活的联系、趣味性以及试题的图文并茂,试题整体给人一种亲切感,能够激发学生的探索兴趣,如2018年第28题(图1).该题虽考查的知识点不多,但要认真分析才能获得答案.
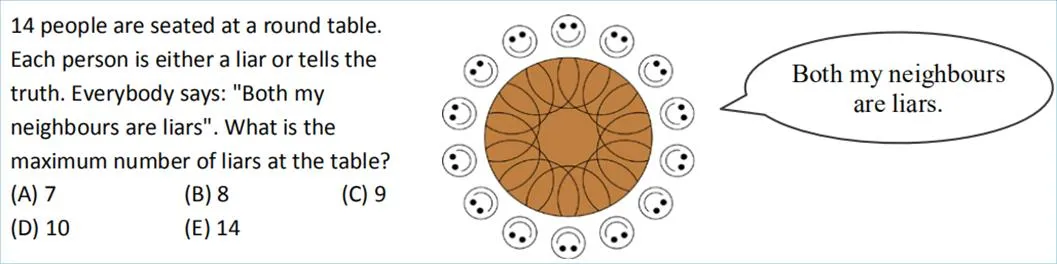
图1 袋鼠赛2018年第28题原题
在上述模型和分析框架的基础上,统计华杯赛和袋鼠赛近6年试题难度的各单因素难度系数和综合难度系数,对中外这两类数学竞赛各单因素难度系数和综合难度系数作均值比较,既分析中外试题各因素难度和综合难度是否存在显著性差异,也揭示中外各影响试题难度的因素的特点,并从中得到启示.
2.1 描述性统计
表2是近6年小学高年级华杯赛和袋鼠赛试题各因素难度系数和综合难度系数的统计表.近6年中的每一年华杯赛试题的综合难度均高于袋鼠赛相应试题的综合难度.华杯赛试题的综合难度最难达到难度系数0.40(2017年),最容易时综合难度系数为0.51(2013年);袋鼠赛试题的综合难度最难时难度系数为0.67(2018年),最容易时综合难度系数为0.72(2013年).近6年华杯赛试题的综合难度系数的标准差为0.04,袋鼠赛试题的综合难度系数的标准差为0.02,华杯赛试题的综合难度的波动性略高于袋鼠赛.近6年华杯赛试题运算难度系数的标准差是0.09,运算难度相对于其它因素难度波动性较大,2016年和2017年华杯赛试题的运算难度相对其它年份较难.根据表2数据,近6年华杯赛在影响试题难度的各个因素的难度系数上都小于袋鼠赛,华杯赛在影响试题难度的各个因素上都比袋鼠赛要求高、难度大.
2.2 差异性检验
为了进一步分析华杯赛和袋鼠赛试题综合难度的差异性特点,研究者对华杯赛和袋鼠赛小学高年级近6年的试题作了各单因素难度系数和综合难度系数均值的差异检验.检验方式为独立样本检验,显著性结果在<0.05水平上为显著水平、在<0.01水平上为极显著水平,并计算Cohen’s值,报告效应量().
由表3可知,华杯赛试题情境因素难度系数均值为0.786 7,袋鼠赛试题情境因素难度系数均值为0.856 7,二者存在极显著差异(=-3.380,=0.007),且效应较高(=0.70),华杯赛试题情境因素难度极显著高于袋鼠赛试题情境因素难度;华杯赛试题信息因素难度系数均值为0.720 0,袋鼠赛试题信息因素难度系数均值为0.886 7,二者存在极显著差异(=0.235,=0.000),且效应极高(=0.92),华杯赛试题信息因素难度极显著高于袋鼠赛试题信息因素难度;华杯赛试题运算因素难度系数均值为0.560 0,袋鼠赛试题运算因素难度系数均值为0.815 0,二者存在极显著差异(=-6.300,=0.001),且效应很高(=0.88),华杯赛试题运算因素难度极显著高于袋鼠赛试题运算因素难度;华杯赛试题推理因素难度系数均值为0.386 7,袋鼠赛试题推理因素难度系数均值为0.536 7,二者存在极显著差异(=-4.478,=0.001),且效应高(=0.79),华杯赛试题推理因素难度极显著高于袋鼠赛试题推理因素难度;华杯赛试题认知因素难度系数均值为0.286 7,袋鼠赛试题认知因素难度系数均值为0.651 7,二者存在极显著差异(=-19.779,=0.000),且效应极高(=0.99),华杯赛试题认知因素难度极显著高于袋鼠赛试题认知因素难度;华杯赛试题综合难度系数均值为0.463 3,袋鼠赛试题综合难度系数均值为0.695 0,二者也存在极显著差异(=-11.267,=0.000),且效应极高(=0.96),华杯赛试题综合难度极显著高于袋鼠赛试题综合难度.
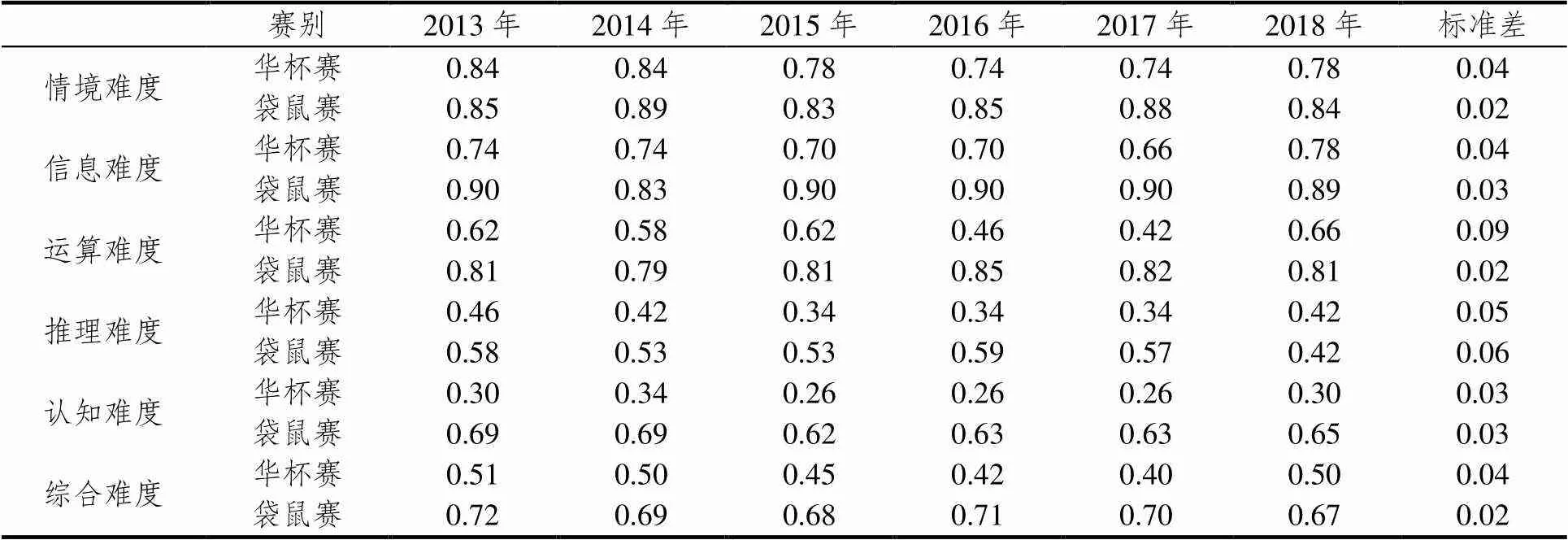
表2 近6年华杯赛和袋鼠赛试题各因素难度以及综合难度统计
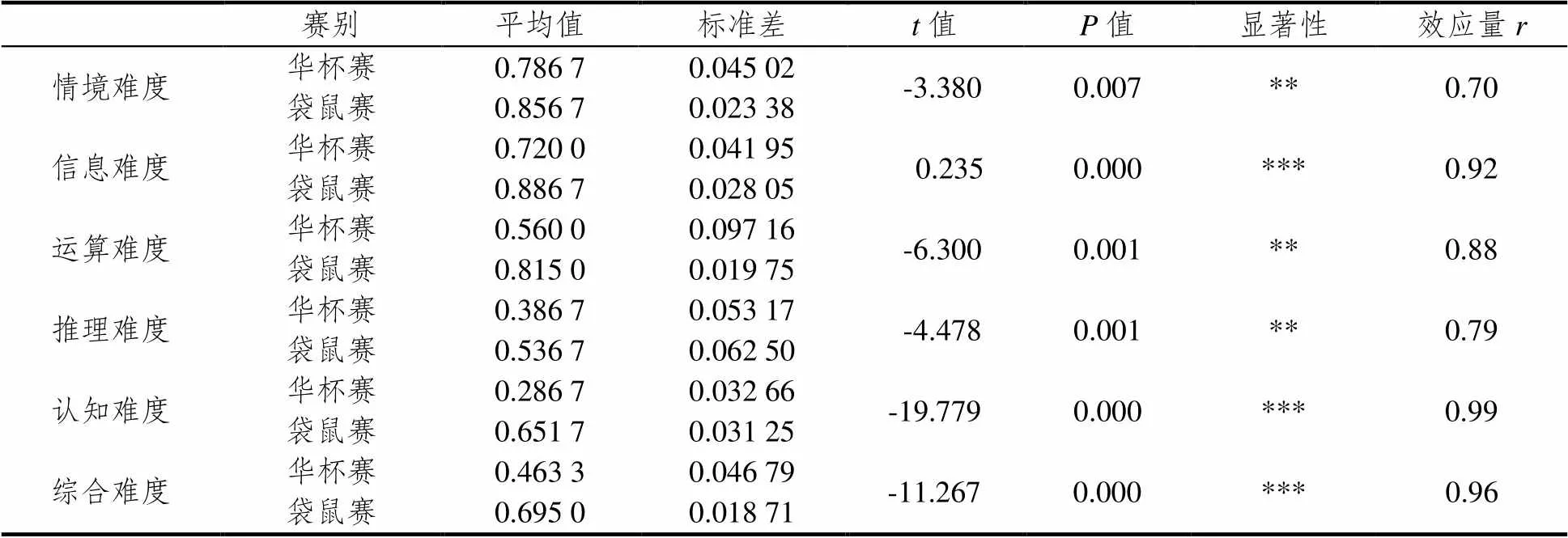
表3 华杯赛和袋鼠赛试题各因素难度以及综合难度的差异性
注:**<0.01,***<0.001
以上数据分析得出的结论是:在影响试题难度的情境、信息、运算、推理和认知5个因素上,华杯赛试题的难度都极显著高于袋鼠赛试题的难度;在信息、运算和认知因素上,华杯赛难度与袋鼠赛难度实际差异更大(在实际中更可能出现显著性差异);在综合难度上,华杯赛试题的综合难度极显著高于袋鼠赛试题的综合难度.
3 讨论与启示
在教育教学活动中,尽管中外各个国家在理念上大多都提倡重视学生学习的主体性,但在实践中往往是国外的一些国家更加注重这一点,在国内则更注重学习的结果和实效.在小学阶段,国外不少国家更重视培养学生的数学兴趣,参与数学竞赛往往是出于学生本人的意愿,数学竞赛成绩也不与升学等高利害活动直接相关,试题难度的设计会充分考虑到多数学生的兴趣和实际认知水平.在国内,虽然小学数学竞赛旨在普及数学、发展学生对数学的兴趣、发现和培养数学资优生,但是在浓厚的考试文化和精英主义导向下数学竞赛的成绩往往与升学挂钩,有很强的选拔性,导致很多学生为了升入好的学校不得不参与小学的各类数学竞赛,功利性目的覆盖了个人兴趣,这就必然要求试题具有较大的难度,只能关注到少部分学生.文化背景不同导致中外小学数学竞赛试题的难度差异较大,但总体而言,培养小学生的数学兴趣是根本,而适当的功利性目标则有助于激发学习动机,应该中西结合通盘考虑,既要普及数学也要有所提高.小学阶段数学竞赛试题的难度应建立在小学生认知水平的一般性特点上,既发展学生的数学兴趣,又提供适当的挑战和提高,因此在命题过程中要控制好试题的难度,命制既有趣又有数学味道的试题.基于这样的考虑和上述数据的比较分析,当下国内小学数学竞赛试题在以下方面值得重视.
3.1 国内小学数学竞赛试题的难度较高应适当降低难度
国内小学数学竞赛试题的难度高于国外同类竞赛试题的难度,这是意料之中的,符合国内的考试文化特点,符合国内大众对小学数学竞赛活动的认识和体验.研究数据显示华杯赛试题的难度极显著高于袋鼠赛试题的难度,同样层次、同样目的的竞赛,国内的试题的确过难.过难的试题将多数学生拒之门外,这在一定程度上可以解释为什么国内的诸多小学数学竞赛活动受到质疑.多年前就有研究者指出:“奥数,因其难,被很多人视为高不可攀”[15],“奥数给学生造成沉重的心理压力,是对学生的一种摧残”[16].这些观点虽值得商榷但也在某种层度上揭示了小学数学竞赛试题过难的现状.袋鼠赛全卷的难度在0.70左右,这意味着多数考生能取得较好的成绩,既有利于大众参与也有利于激发兴趣;华杯赛全卷的难度在0.46左右,这使得大部分学生的得分较低、在考试中失意,受到打击.如果将来要开展小学数学竞赛活动,那么国内小学数学竞赛应注意适当降低难度,使得学生在竞赛活动中有获得感,避免竞赛活动沦为单一的考试选拔工具,偏离数学竞赛活动最重要的普及数学文化、发现数学人才和培养数学兴趣的本质精神.
3.2 国内小学数学竞赛应进一步处理好普及与提高的关系
小学数学竞赛处理好普及与提高的关系不应只是口号.尽管有研究者曾经指出:“应该把握好日常而平凡的数学课堂,如果仅通过数学竞赛来普及数学,有舍本逐末之嫌.”[17]事实上数学竞赛活动与日常数学教学并不矛盾,数学竞赛有竞技性和提高性,竞赛活动普及数学的重要价值毋庸置疑,关键在于如何做好和落实.这要求正确认识数学普及,处理好普及与提高的关系.数学普及不是把大学或中学的知识内容一概下放到小学,数学普及也不是让大众去学习很多超出小学生认知水平的方法和技巧,数学普及是要让小学生喜欢数学、认识到数学的价值、了解数学最基本的思想和方法,进而愿意亲近数学,从而逐步发展数学思维和能力.一项在上海的调查研究显示,学无余力和难以学好是小学生不参加数学竞赛两个重要的因素[18],试题过难导致很多小学生不再参加小学数学竞赛,并且使得很多小学生误解数学、远离数学,小学数学竞赛普及数学的作用随之烟消云散.普及与提高是辩证统一的,普及是主要的、根本的,不普及就不会有整体的提高,普及是提高的基础,提高是普及的发展和目的.普及数学的关键在于激发学生对数学的兴趣,要激发学生的兴趣首先要让学生了解数学,了解真正的、简洁的、美的数学,小学数学竞赛本应该是一个很好的平台,是学生领略数学美的一扇窗.这扇窗应该为多数小学生打开,让更多的人能够通过这扇窗体悟数学的价值,而不是让这扇窗设得太高、开得太窄以至于多数学生在窗台之下.
3.3 国内小学数学竞赛试题应重视情境创设并贴近学生认知水平
小学五、六年级学生的认知水平已经逐渐从具体思维阶段过渡到抽象思维阶段[19],但这个阶段的学生思维活动仍需要具体内容的支持,尤其是日常生活中喜闻乐见事物的支持.任何高层次的思维都是由具体进至抽象,因此试题要结合图形、图表和图画等尽可能形象化地展现.袋鼠赛受欢迎的重要原因之一就是其试题的情境多为生活背景(如上述袋鼠赛2018年第28题),学生见之有亲切感.而华杯赛试题则不少是直接从数学出发(如上述华杯赛2018年的第5题),于小学生而言就相对缺少生活气息和趣味性,无法激起大部分学生的探究兴趣.鉴于小学生的心理特点,熟悉的、形象化的、生活化的情境背景对于他们思考和解决问题非常重要.国内小学数学竞赛试题在问题情境上应更加自然和生活化.此外,试题在认知要求上应更贴近小学生的思维水平.不论是发展数学兴趣还是发现数学资优生,并不是试题越难越好.适度的提高是必要的,也正是因为提高性和竞技性才使得数学竞赛称之为数学竞赛,但不能过度拔高,无视小学生的认知水平规律.正如有些专家所指出的,小学数学竞赛应当重视学生对于基础数学知识的灵活应用能力[20],而不是追求知识的偏和难以及琐碎的技巧,更不是把中学数学甚至高等数学的思想和内容不加“修饰”地直接放进小学数学竞赛.
[1] 华罗庚金杯少年数学邀请赛简介[EB/OL].(2019-03-08)[2019-03-10]. http://www.huabeisai.cn/list1.vpage? colId=1.
[2] Math Kangaroo in USA. Latest updates [EB/OL]. (2018-12-19) [2019-03-08]. http://www.mathkangaroo.us/mk/ default.html.
[3] 李叶峰,梁蓉.小学奥数热的冷思考[J].教育探索,2009(11):52-53.
[4] 毛竞飞.高考命题中试题难度预测方法探索[J].教育科学,2008,24(6):22-26.
[5] 高文君,鲍建生.中美教材习题的数学认知水平比较——以二次方程及函数为例[J].数学教育学报,2009,18(4):57-60.
[6] 汤服成.数学模糊抽象难度的研究简介[J].数学教育学报,1998,7(4):48-51.
[7] 谢莹,许荣斌.基于深度置信神经网络的组卷难度预测[J].韶关学院学报,2018,39(9):15-19.
[8] 鲁庆云,宋乃庆.我国数学试题难度影响因素的研究综述[J].数学通报,2009,48(4):47-49.
[9] 王建波.中美澳初中数学统计课程难度的比较研究[J].数学教育学报,2017,26(4):50-55.
[10] 曹一鸣,吴立宝.初中数学教材难易程度的国际比较研究[J].数学教育学报,2015,24(4):3-7.
[11] 鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望,2002,31(9):48-52.
[12] 陈燕,王祖浩.高考实验题“绝对难度”评估工具的研究[J].全球教育展望,2013,42(2):45-53.
[13] 章建石.新高考改革背景下不同版本试卷测量学指标的比较与监测——以某年度英语试卷的分析为例[J].全球教育展望,2018,47(5):71-80.
[14] 武小鹏,张怡.中国和韩国高考数学试题综合难度比较研究[J].数学教育学报,2018,27(3):19-24,29.
[15] 唐越桥.从小学教师专业化发展看奥数的价值[J].当代教育理论与实践,2013,5(7):23-26.
[16] 薛寒.顾明远呼吁:奥数班早就该停了[J].中国教育学刊,2009(10):25.
[17] 游安军.也论中国数学竞赛的教育性质——与罗增儒先生商榷[J].数学教育学报,2009,18(1):48-51.
[18] 伍青生.五年来上海市小学生校外奥数学习状况调查[J].上海教育科研,2015(4):27-31.
[19] 朱智贤,林崇德.思惟发展心理学[M].北京:北京师范大学出版社,1986:328.
[20] 孔企平,张晓玲.从学生数学学习的规律看“奥数”热[J].全球教育展望,2004,33(5):70-72,80.
A Comparative Study on the Difficulty of Chinese and Foreign Math Contests for Elementary School Seniors——Huabei Contest and Math Kangaroo
JIANG Pei-jie1, 2, ZHANG Yong1, 2, XIONG Bin1, 2
(1.School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;2. Shanghai Key Laboratory of PMMP, Shanghai 200241, China)
The difficulty of the questions in the math contests is closely related to the popularization of mathematics and the social response to the contests itself. This paper discusses the difficulty of the current math contests questions in primary schools at home and abroad and addresses the question whether the questions of the contests in China are more difficult than those in other countries. This paper firstly constructs a multi-factor model of the comprehensive difficulty of mathematics contests questions in primary schools on the basis of the existing model; then, it compares the comprehensive difficulty of the questions of Huaibei contest and Math Kangaroo in grade 5 & 6 of the past six years. SPSS22 is used to analyze the data. On the basis of taking into account the differences between Chinese and foreign national conditions and cultural traditions, the following conclusions of primary school math contests are drawn: (1) The difficulty of the questions in primary schools in China is much higher than that in other countries and the difficulty should be reduced appropriately; (2) The relationship between mathematics popularization and improvement in Chinese math contests should be dealt with further; and (3) The questions in Chinese math contests should be more lifelike in the situation and closer to the pupils’ thinking level in cognition.
math Kangaroo; Huabei contest; difficulty; elementary mathematics contest
G629.1
A
1004-9894(2020)06-0087-05
蒋培杰,张勇,熊斌.中外小学高年级数学竞赛试题难度的比较研究——以“华杯赛”与“袋鼠赛”为例[J].数学教育学报,2020,29(6):87-91.
2020-06-20
上海市核心数学与实践重点实验室课题——数学实践(18DZ2271000)
蒋培杰(1990—),男,广西全州人,博士生,主要从事数学方法论与数学教育研究.
[责任编校:周学智、陈隽]
