高考数学全国Ⅰ卷与课程标准的一致性研究——以2007—2019年为例

伊西凡，孙佳宁，朱立明

高考数学全国Ⅰ卷与课程标准的一致性研究——以2007—2019年为例

伊西凡1，孙佳宁1，朱立明2

（1．东北师范大学 数学与统计学院，吉林 长春 130024； 2．唐山师范学院 教育学院，河北 唐山 063000）

为了解当前新高考改革背景下高考数学试卷命题改革发展方向，基于“SEC”分析模式提出一套面向课程标准的编码准则，由“一级（二级）内容主题”及其对应的“认知水平”，量化得到两组代表粗细尺度的二维矩阵．对2007—2019年数学全国Ⅰ卷与课程标准进行一致性分析，并结合皮尔逊模型进行检验．结果显示：在粗细两种尺度下一致性系数取值的区间范围有较大不同，但呈现出相似的变化趋势；认知水平分布在新高考改革前后呈现出不同的分布特征，展示了近年全国Ⅰ卷为适应高考整体改革而在命题环节中进行的重大调整．这些成果可以为迎接新高考的中学数学教学，科学命制高考数学试题，深入实施新课程标准提供积极的建议．

新高考；高考数学全国Ⅰ卷；数学课程标准；一致性量化分析；SEC模式

1 问题提出

高考作为中国选拔人才的重要途经，兼具“毕业性”与“选拔性”的双重性质，其内容和形式受到众多教育工作者和大众的关注．一直以来，中国对于课程标准与高考试题的改革都十分谨慎[1]．2003年4月，国家教育部颁布了《普通高中课程改革方案（实验）》（以下简称：课标（实验））作为中国指导学科建设、课堂教学、教材编写、教学实施、考试命题与评价的最高准则[2]；为配合课标（实验）的实施，2007年，国家命题组在宁夏拉开了全国Ⅰ卷命制的序幕；2018年1月，随着中国颁布《普通高中数学课程标准（2017年版）》（以下简称：课标（2017年版）），意味着中国第八次课程改革进入全面深化阶段[3]．至2020年止，全国卷对课程标准的实践与落实已有13年，十余年来，课标（实验）与新课标卷的一致性如何？一致性趋势是否随着课标（2017年版）的颁布产生变化？造成变化的原因是什么？

研究基于粗细两种尺度（粗尺度：“一级内容主题—认知水平”；细尺度：“二级内容主题—认知水平”的二维矩阵），利用SEC一致性模式定量研究中国数学全国Ⅰ卷与课标（实验）的一致性及其13年以来的变化趋势，并对两种尺度下一致性的相关关系进行皮尔逊检验．总结13年来全国Ⅰ卷的命制特征，根据特征观察2017年新高考改革前后一致性的差异，从内容主题与认知水平两方面分析造成不同阶段一致性差异的原因．以此了解当前新高考改革背景下高考数学试卷命题改革发展方向，以期对科学命制高考数学试题、深入实施课程标准下的有效数学教学提供方向和建议．

2 文献综述

对于课程标准与学业评价、课程教材一致性的研究一直是中国教育学界关注的热点问题．起初各个学者对美国几种一致性研究分析模式进行论述和本土化研究，而后逐渐应用到各个科目中进行实践分析．在新高考提出以后，新课程标准对数学教学、试卷命制的所提出的新要求也正是国内学者所关注的重点．

刘学智[4]、张雨强[5]等人介绍了几种一致性分析模型及其本土化探索与应用[6-8]，为教科书、试卷与课程标准一致性水平分析提供了新的分析框架和方法．

近年来，孔凡哲[9]、张定强[10]、缪琳[11]等人分别利用韦伯、SEC、Achieve模式从化学、数学、语文、物理等学科分析了学业评价、课程教材与课程标准的一致性．相关结论对指导今后学业评价、高考试题命制以及课程标准改革具有巨大意义[12-14]．以上几位学者分析的方向多为某一年或者某几年的高考试题、初高中学业水平考试、教材与课标的一致性，在多年份的一致性上并不具有连续性．仅有赵宁宁[1]研究了近40年语文高考试卷与课标的一致性，将语文试卷根据特征特点的不同进行了阶段性分类，发现在教育改革阶段一致性系数不稳定．对于新高考背景下，数学学科上连续多年且不同内容主题尺度下的一致性分析的检验与比较，目前国内研究还未涉及[2]．

3 研究设计

3.1 研究对象

自2018年国家颁布《普通高中数学课程标准（2017年版）》以来，国家在上海、浙江等地逐步实施了新高考改革，但是新课标I卷所涉及的省份尚未实施改革．为减少变量，增加研究连续性，在课程标准上统一采用课标（实验），以观察13年以来数学全国Ⅰ卷与课标（实验）的一致性变化趋势．

在试卷上选择2007—2019年普通高等学校招生全国统一考试理科数学Ⅰ卷（简称：**年全国Ⅰ卷）．

3.2 研究工具

3.2.1 “SEC”一致性分析研究模型

一致性分析研究模型起源于20世纪90年代美国学者诺曼韦伯提出的Webb模式．2001年，史密斯与帕特等人在借鉴了Webb模式的基础上，由CCSSO协助，合作开发了更为科学的SEC一致性分析模式（Surveys of Enacted Curriculum——课程实施调查），作为实施监测的权威工具在美国进行了广泛应用．该模式的核心是“内容主题—认知水平”的二维矩阵[4]．其过程主要分为3个阶段．

第一阶段：“内容主题—认知水平”二维矩阵的构建；

第二阶段：研究资料统计，计算学业评价与课程标准所涉及的学习目标数量与学习目标总量的比率；

第三阶段：利用计算得出的比率代入Porter一致性系数公式[10，15]：

其中，——二维矩阵中单元格的数量；

——每一个单元格（1≤≤）；

——一致性系数（介于[0, 1]之间，0表示不一致，1表示完全一致）[6，16-17]．

3.2.2 难度系数公式

难度系数反映试题的难易程度，即考生在一个试题中的失分程度．根据某省招生办公室信息管理处提供的2008—2019年新课标全国Ⅰ卷（理科）中每一道题目的平均分，计算出每一道题目的难度系数，由此对认知水平进行划分．难度系数：

其中，——题目的平均分；

——题目的分值；

——难度系数（介于[0, 1]之间，(0, 0.3]表示难度较低，(0.3, 0.7)表示难度一般，[0.7, 1]表示难度较高．

3.2.3 皮尔逊相关系数（PCCS）

3.2.4 归一化公式

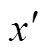
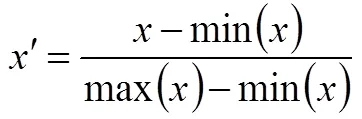
3.3 研究过程

3.3.1 确定编码准则

（1）课标编码准则．

①内容主题编码准则．

根据课标中课程结构与课程内容的设置，对课标（实验）进行编码．编码原则为：

首先，将基础知识、函数、几何与代数、概率与统计作为一级知识主题进行粗尺度编码1、2、3、4；其次，对4个一级主题下的24个二级知识主题进行细尺度编码1.1、1.2……；接下来，对24个二级知识主题下的67个目标领域作为三级知识主题编码1.1.1、1.1.2……；最后，对67个三级知识主题下的170个目标知识点作为四级知识主题进行编码1.1.1.1、1.1.1.2……．具体如表1．

表1 内容主题编码

② 认知水平编码准则．

以布鲁姆认知领域中的行为目标为依据，结合SEC认知水平编码的可操作性以及中国数学学科课程标准三维目标中的行为动词分析．将认知水平按照由低到高的顺序依次划分为：认知水平A（知道）、认知水平B（理解）、认知水平C（掌握），分别对认知水平进行编码．每种水平的界定如表2．

表2 认知水平的界定

四级知识主题的认知水平用A、B、C编码，如“1.1.1了解集合的含义，体会元素与集合的属于关系”属于“认知水平A（知道）”领域，用“A”进行编码．当一个四级知识主题包含多个学习内容和认知水平时，处理方法如下[13]．

（Ⅰ）四级知识主题表述的是同一内容的不同水平的行为动词时，只需要考虑最高一级的认知水平编码．如“2.7.1.4理解函数的单调性、最大（小）值及其几何意义；了解函数奇偶性的含义”，“理解”属于“认知水平B”，“了解”属于“认知水平A”，所以在编码的时候只需要考虑最高层次，用“B”编码．

（Ⅱ）四级知识主题表述的是同一行为动词的不同内容时，编码时按照正常情况编码．如“1.1.2.1理解集合之间包含与相等的含义，能识别给定集合的子集”包含“理解”“识别”编码为“B”．

（Ⅲ）四级知识主题表述的是不同内容，且有两个或以上不同水平的行为动词时，那么，按照内容与水平进行拆分为两个及以上的四级知识主题进行编码．如：“了解算法的含义，了解算法的思想；理解程序框图的3种基本逻辑结构：顺序结构、条件分支、循环结构”在绘制编码时拆分为“1.2.1.1了解算法的含义，了解算法的思想”和“1.2.1.2理解程序框图的3种基本逻辑结构：顺序、条件分支、循环”，分别编码为“A”和“B”．

（2）高考试卷编码准则．

①内容主题编码准则．

分析每一道试题所考查的知识点，以课标中编码过的内容主题作为依据，当知识种类一致时，由一位在职骨干教师在试题上标出对应课标上内容主题的编码．具体示例如图1与表3．

图1 2019年普通高等学校招生全国统一考试第1题

表3 高考试卷内容主题编码

②认知水平编码准则．

根据某省招生办公室提供的2007—2019年全国Ⅰ卷评析中所给的每一道题的平均分，计算出每一道题目的难度系数，对于难度系数介于(0, 0.3]编码为“认知水平A”，介于(0.3, 0.7)编码为“认知水平B”，介于[0.7, 1]编码为“认知水平C”．

（3）编码人员．

4位编码者分别由一位教授、一位博士研究生、一位在职数学教师和一位硕士研究生构成（均具有数学与教育学背景），各自根据课标与试题的编码准则进行编码，各自得到两种尺度下的二维矩阵，得出各自分析的结果．经计算，4位编码者对课标与试卷分析的信度分别为0.958与0.932，说明具有良好的内部一致性．对于存在分歧的地方，4位编码者通过协商达成一致，形成最终结果．

3.3.2 构建二维矩阵

根据课程标准编码原则与高考试卷编码原则，得到课标（实验）与2007—2019年全国Ⅰ卷在“一级内容主题—认知水平”（简称：粗尺度）与“二级内容主题—认知水平”（简称：细尺度）两个尺度下的二维矩阵．以课标二维矩阵为示例，如表4和表5．

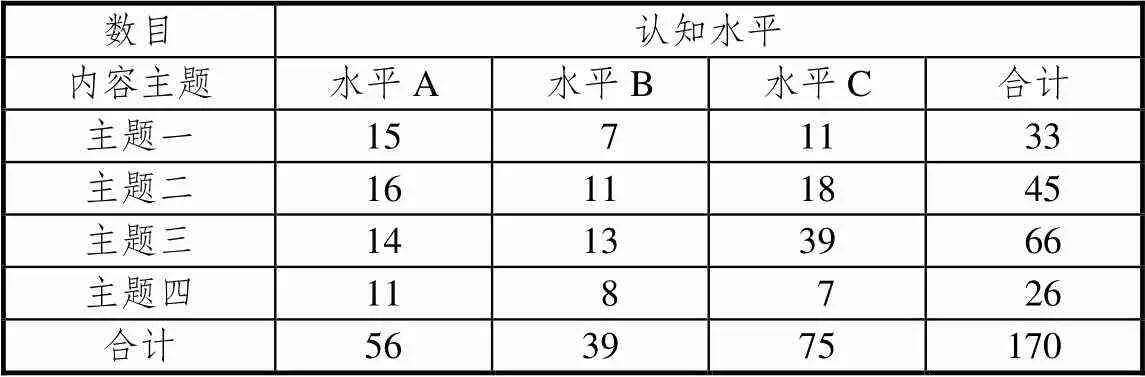
表4 课标在粗尺度下的二维矩阵

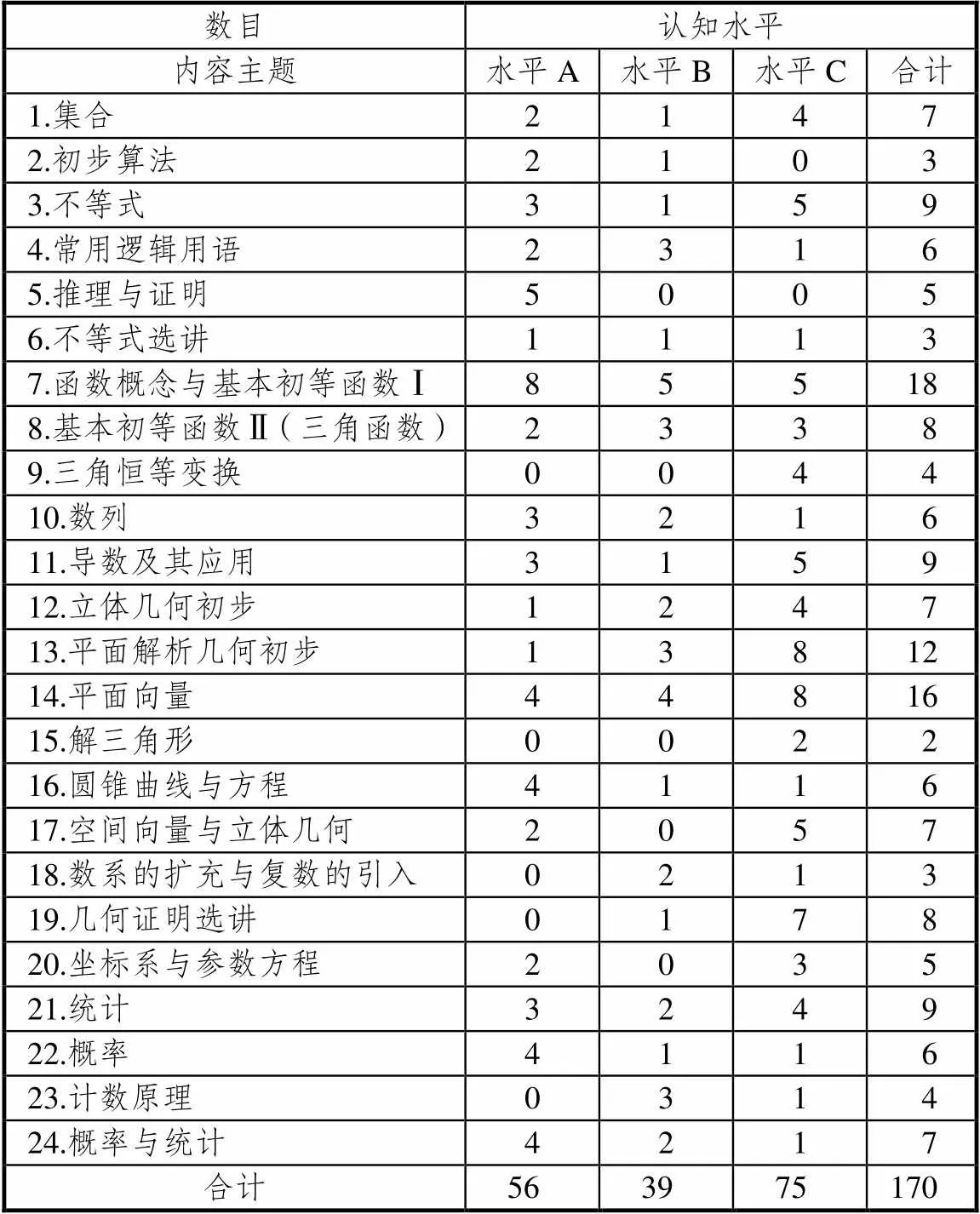
表5 课标在细尺度下的二维矩阵

4 研究结果

4.1 整体一致性分析

4.1.1 粗尺度下的一致性结果

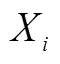
从图1粗尺度下的一致性系数可以得到，2007—2019年全国Ⅰ卷与课标的一致性系数均值为0.747，整体一致性程度较高，达到统计学中的显著性．其中一致性程度最好的是2016年，一致性系数达到0.812；一致性系数较差的是2017年，一致性系数为0.670．

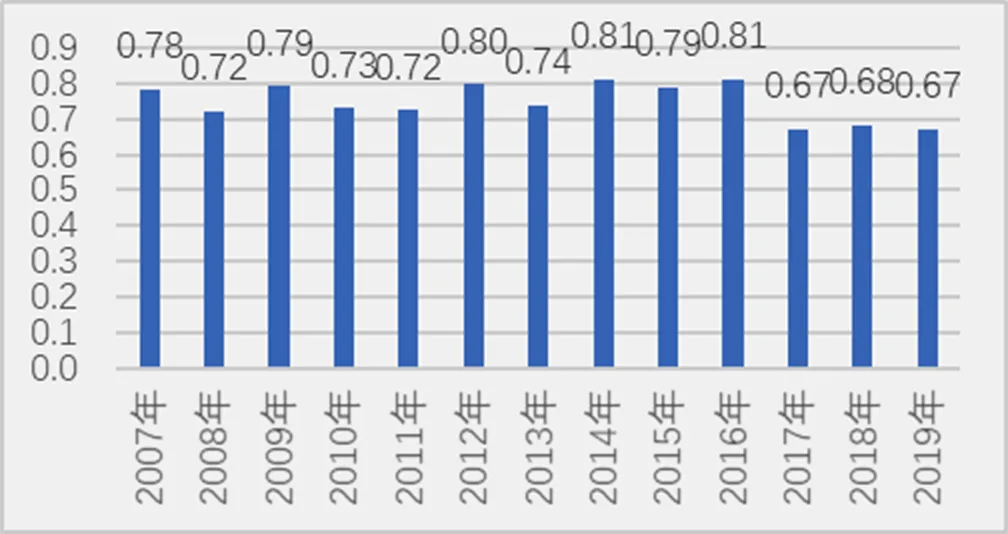
图2 粗尺度下的一致性系数

从一致性稳定情况上来看，2007—2016年的一致性系数较高（均值：0.769），一致性系数程度从低到高为：2016年、2014年、2012年、2009年、2015年、2007年、2013年、2010年、2011年、2008年；而在课标（2017年版）颁布以后，一致性系数降低（均值：0.673），从低到高依次为：2017年、2019年、2018年．

4.1.2 细尺度下的一致性结果

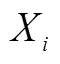
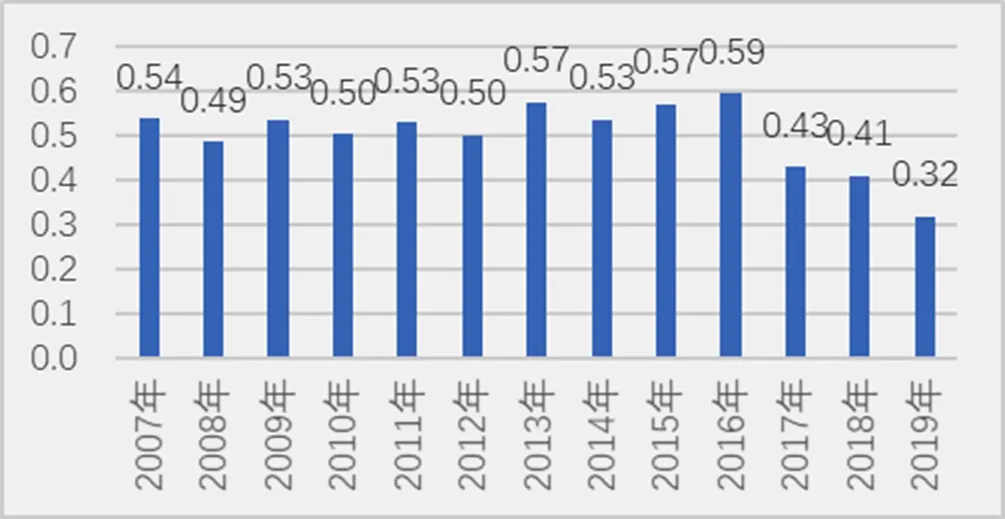
图3 细尺度下的一致性系数

从图2一致性系数可以得到，相较粗尺度的一致性系数而言，细尺度下2007—2019年全国Ⅰ卷与课标（实验）的整体一致性程度偏低（均值：0.501）．最高为2016年（0.593 7），最低为2019年（0.316 6）．

从一致性稳定情况上来看，2007—2016年的一致性系数较为稳定，均在0.5附近．课标（2017年版）颁布以后，一致性系数呈现断崖式下降，均在0.4附近．

4.1.3 两种尺度下一致性系数变化趋势的相关关系

将图1中在粗尺度下的一致性系数与图2中细尺度下的一致性系数分别代入归一化（rescaling）公式，计算出归一化后的两组数据（分别简称为：粗尺度归一、细尺度归一）．具体如图4所示．

观察图3可知，两组一致性系数变化趋势大致相同，将2007—2019年归一化后的两组数据代入皮尔逊相关系数（PCCS）公式，得到相关系数为0.786 3，呈现出强正相关的相关关系．

从一致性系数的稳定程度上来看，可以发现两种尺度下的一致性系数在2007—2016年稳定在某个区间范围内，而在2017年以后一致性系数降低，且不太稳定，由此可将课标（实验）与全国Ⅰ卷的一致性划分为两个阶段：第一阶段（2007—2016年），第二阶段（2017—2019年）．在两种尺度下均是第一阶段的一致性系数较高，第二阶段的一致性系数较低．

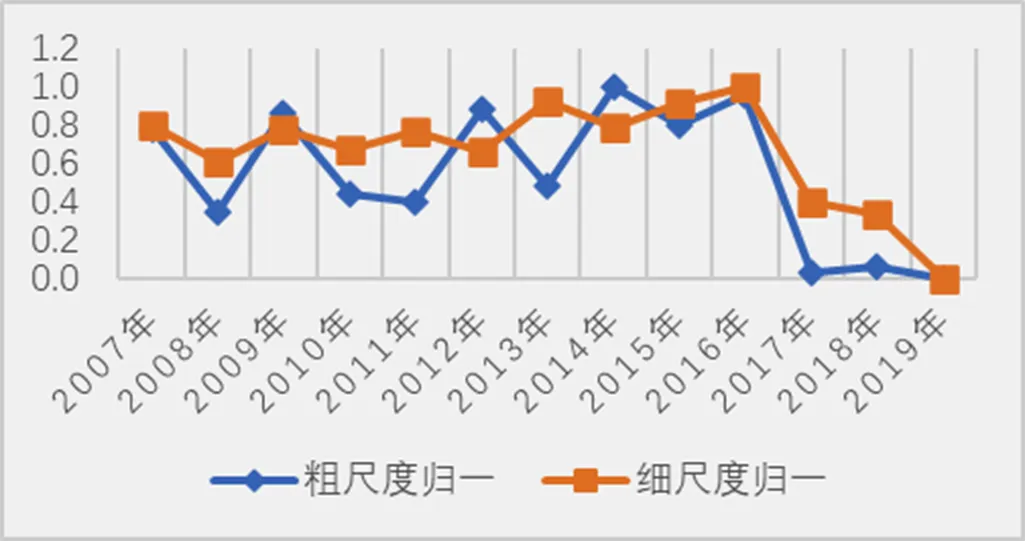
图4 归一化后两组一致性系数变化趋势

4.2 内容主题一致性

4.2.1 一级内容主题的一致性

将4个一级内容主题，在13套全国Ⅰ卷和课标中的比率分别以簇型柱状图和直线图的组合形式展现，以便更清晰地展现各年份在不同知识主题上的侧重程度，并与课标要求比率进行比较．具体如图5所示．

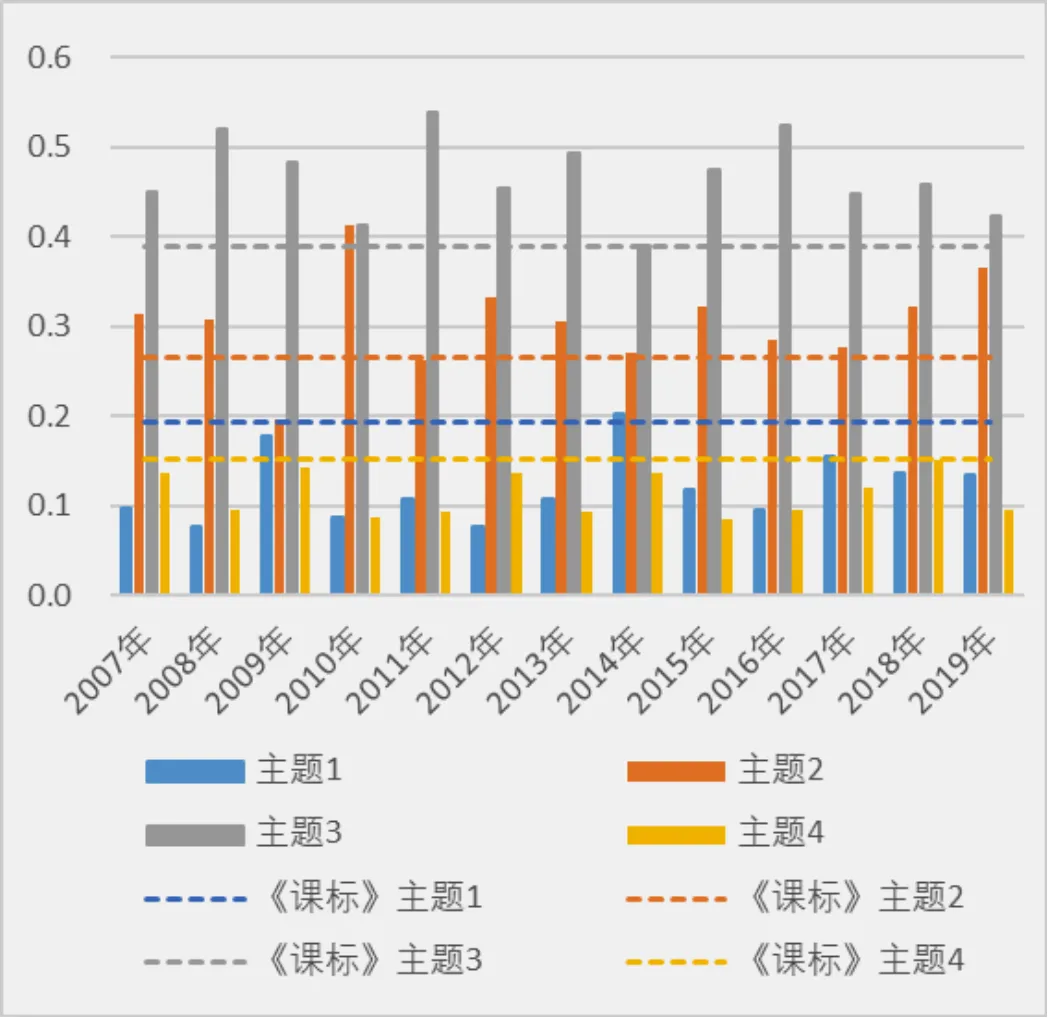
图5 课标与13套全国I卷一级内容主题比率分布

从课标要求上来看，主题3几何与代数部分比率最高（0.388 2），主题2：函数部分比率其次（0.264 7），主题1：基础知识再次之（0.194 1），主题4：概率与统计部分最低（0.152 9）．

纵观13套试卷而言，全国Ⅰ卷最注重考查的部分是主题3，考查比率超出课标要求的考查比率，其中2011年比率最高（0.538 5），2014年份最低（0.389 8）；其次是主题2，仅有2009年一年试卷的考查比率（0.214 3）低于课标要求，其余年份试卷均高于课标要求，考查比重较高，其中2010年的最高（0.413 8）；在主题1：基础知识部分，13套试卷的考查比率大都低于课标比率，仅有2014年一年（0.203 4）的试卷达到了课标要求，考查注重程度较低；在主题4：概率与统计部分，13套试卷的考查比率全部低于课标比率，仅有2009（0.142 9）和2018年（0.15）接近达到课标比率，考查比率最低．

4.2.2 二级内容主题的一致性

将24个二级内容主题在13套全国Ⅰ卷以等高线热力图的形式展现，以便更清晰地展现在不同二级内容主题与年份上的侧重程度，权重大小以颜色作为区分，权重比例由高到低依次为：红色（0.2~0.25）、黄色（0.15~0.2）、蓝色（0.1~0.15）、橘红（0.05~0.1）和灰色（0~0.05）．具体如图6所示．

由图6可以看出课标对24个二级知识主题考查权重最高的几个内容为：函数概念与基本初等函数Ⅰ（0.106）、平面向量（0.094）、平面解析几何初步（0.071）、不等式（0.053）、统计（0.053）、导数及其应用（0.053）．纵观13年全国Ⅰ卷，在函数概念与基本初等函数Ⅰ、导数及其应用、立体几何初步、圆锥曲线与方程和空间向量与立体几何这5个方面考查权重均超出课标要求．

图6 课标与13套全国I卷二级内容主题比率的地形等高线

4.3 认知水平一致性

将3个级别的认知水平在13套全国Ⅰ卷与课标中的比率分别以簇型柱状图和虚线图的组合形式展现，以便更直观地展现各年份在不同主题上的侧重程度，并与课标要求比率进行比较．具体如图7所示．

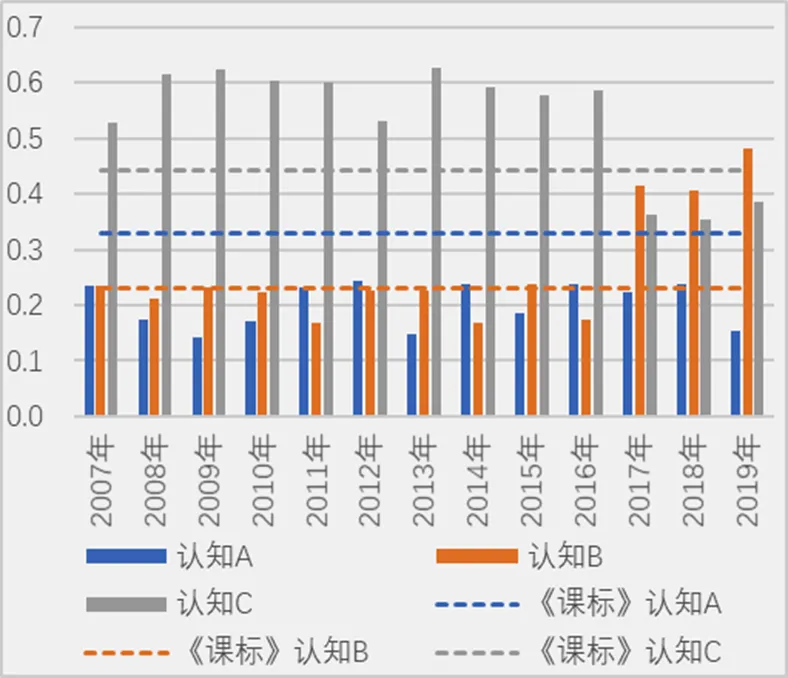
图7 课标与13套全国I卷认知水平比率分布

从课标要求上来看，认知水平C比率最高（0.441 2），认知水平A其次（0.329 4），最低为认知水平B（0.229 4）．

纵观13套试卷而言，新课标全国Ⅰ卷在在认知水平的稳定程度上呈现出两个阶段．第一阶段：2007—2016年；第二阶段：2017—2019年．在第一阶段中，认知水平C考查比率均超出课标要求，从高到底依次为：2013年（0.626 7）、2009年（0.625 0）、2008年（0.615 4）、2010年（0.613 4）、2010年（0.600 0）、2014年（0.593 2）、2016年（0.587 3）、2015年（0.576 3）、2012年（0.530 3）、2007年（0.529 4）；而在第二阶段，接近达到课标要求．认知水平A两个阶段中的考查比率基本均未达到课标要求，且考查比率相差不大，均在0.22左右．在认知水平B的考查中，第一阶段：基本达到课标标准，最低为2011年（0.169 2），最高为2015年的（0.237 3）；而在第二阶段的考查中，均超过课标要求，从高到低依次为：2019年（0.480 8）、2017年（0.413 8）、2018年（0.406 8）．

5 研究结论

5.1 粗细尺度下一致性系数的变化趋势

观察2007—2019年在两种尺度下的一致性系数（见图2和图3），均是在粗尺度下的一致性较高，在细尺度下的一致性较低．同时，计算在两种尺度下一致性的皮尔逊系数(0, 7 836)，可以得到两组一致性系数的变化趋势具有较高的正相关关系（如图3），说明SEC模式在不同尺度下量化中国学业评价与课标具有较高的适用性和稳定性．

5.2 粗细尺度下一致性的两个阶段

根据粗细尺度下一致性的变化趋势，将全国Ⅰ卷的一致性分析分为两个阶段，第一阶段：2007—2016年，在粗细尺度下一致性系数相对于整体均偏高；第二阶段：2017—2019年，在粗细尺度下一致性系数相对于整体均偏低．考虑到中国在2018年1月，颁布了《普通高中数学课程标准（2017年版）》，可以发现，虽然全国Ⅰ卷所设计的省份并未进行新高考全面改革，但是近年全国Ⅰ卷为适应高考整体改革而在命题环节中也进行了重大的调整变化．

5.3 内容主题的一致性

观察在各年份全国Ⅰ卷在不同尺度的内容主题分布与权重图（见图5和图6），发现内容主题的分布情况在各年份保持高度一致，与课标要求分布均有相同的差异．由此可知，造成两个阶段（2007—2016年，2017—2019年）一致性系数差异的原因不是由内容主题分布造成的．

一级内容主题分布：根据不同年份在一级内容主题上的分布（见图5），发现均是主题二函数部分考查比率最高（超出课标要求），主题三几何与代数其次（超出课标要求），主题一：基础知识与主题四：统计与概率的考查比例相差不大，各年份在一级内容分布上考查比率相差不大．

二级内容主题分布：根据不同年份在一级内容主题上的分布（见图6），可以看出13套试卷在二级主题上权重图具有较高的一致；在数列、导数及其应用、立体几何初步、解三角形、圆锥曲线与方程、空间向量与立体几何部分，每年权重均比课标要求高，而在常用逻辑用语、推理与证明、三角恒等变换、统计与概率考查比例较低．

5.4 认知水平的一致性

在内容主题的分布上，各年份与课标的差异保持高度的一致．造成一致性系数分成两个阶段的原因到底是为何？在此基础上分析了各年度试卷在认知水平上的差异性．

观察课标与13套新课标全国Ⅰ卷认知水平比率分布情况（如图6），可以发现两个阶段在认知水平的分布上呈现出巨大差异，第一阶段的认知水平分布较为一致，认知水平C考查远超课标要求，认知水平A与认知水平B考查程度相差不大；而在第二阶段中，认知水平C的考查比重大幅度下降，认知水平B的比重大幅度上升；由此可知造成两个阶段一致性系数发生大幅度变化的原因是由于认知水平分布情况的变化．

6 思考与建议

第一，量化课程标准，让教与评有迹可循．高中数学课程标准是数学学科教学、数学教科书的编辑以及考试评价的重要标准，应当具有可操作性与科学性．虽然目前课标（2017年版）在内容主题上所覆盖的“广度”具有相当明确的规定与要求；但是在知识“深度”即认知水平划分上较为粗略，仅将其划分为“了解”“理解”“掌握”3种水平，但每种水平并未进行具体界定．对指导教师实际教学内容的深度与命题人对于试卷命制难易程度的把握上造成较大的困难，致使试卷与课标的一致性产生偏差．

第二，深化教育课程改革，实现教与标一体化．虽然全国Ⅰ卷所涉及的地区并未全面进行新高考改革，但是从一致性系数上看，2017年以后的试卷与课标（实验）的一致性降低，可见，全国Ⅰ卷已经根据新高考要求进行了试题命制上的改革．基于此，在实际教育教学中开展课标（2017年版）与教学、试题的一致性研究，对于新课程改革在实际教学与试题命制的深化改革会起到巨大的推进作用[18]．

第三，完善试卷命制体系，全面提高试卷质量．在命制全国Ⅰ卷的过程中，应紧扣新高考改革方向，与课标（2017年版）的要求相匹配[19]．降低高考试题中函数概念与基本初等函数Ⅰ、导数及其应用、立体几何初步、圆锥曲线与方程和空间向量与立体几何部分考查的难度，提高统计与概率、常用逻辑用语、推理与证明部分考查的频率，将会使得全国Ⅰ卷更符合新高考改革后在内容主题上与认知水平上的要求．

[1] 赵宁宁，张开，海春英，等．我国40年语文高考试卷分析及反思[J]．课程·教材·教法，2018，38（5）：26-36．

[2] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003：10．

[3] 陈婷，孙彬博，张彩云．百年高中数学课程能力目标发展的回眸与反思——基于课程标准（教学大纲）的文本分析[J]．数学教育学报，2019，28（6）：5-9，54．

[4] 刘学智，马云鹏．美国“SEC”一致性分析范式的诠释与启示——基础教育中评价与课程标准一致性的视角[J]．比较教育研究，2007，29（5）：64-68．

[5] 诺曼·韦伯，张雨强．判断评价与课程标准一致性的若干问题[J]．比较教育研究，2011，33（12）：83-89．

[6] 杨玉琴，王祖浩，张新宇．美国课程一致性研究的演进与启示[J]．外国教育研究，2012，39（1）：113-121．

[7] 刘学智，张雷．学业评价与课程标准的一致性：韦伯模式本土化探究[J]．外国教育研究，2009，36（12）：13-17．

[8] 岳喜腾，张雨强．基于课程标准的学业成就评价：韦伯模式之研究[J]．全球教育展望，2011，40（10）：79-85．

[9] 孔凡哲，张丹丹，周青．合作问题解决在人教版小学数学教科书中的呈现及与课程标准的一致性分析[J]．课程·教材·教法，2019，39（2）：92-99．

[10] 张定强，裴阳．新高考改革背景下数学试卷与课标一致性研究——以2017—2018年全国Ⅱ卷与浙江卷为例[J]．数学教育学报，2019，28（4）：55-60．

[11] 缪琳，陈清华，苏圣奎．义务教育课程标准与中考试卷一致性分析——以2013—2016年厦门市中考数学试卷为例[J]．数学教育学报，2017，26（5）：44-48．

[12] 徐帆，张胜元，孙庆括．初中数学学业评价与课程标准的一致性研究——以福建省五套中考数学试卷为例[J]．数学教育学报，2019，28（3）：98-102．

[13] 张志红，张雨强，周传昌．化学中考试题与课程标准的一致性初探[J]．化学教育，2010，31（9）：44-46．

[14] 刘学文，韩庆奎，郭敏，等．高中化学学业水平考试与课程标准的一致性分析[J]．化学教育，2015，36（17）：49-54．

[15]  NORMAN L W. Alignment of science and mathematics standards and assessments in four states [M]. Washington D C: Council of Chief State School Officers, 1999: 23.

[16] 李秋实，刘学智．美国“课程实施调查”项目新进展：教科书与课程标准一致性分析模式研究[J]．外国教育研究，2019，46（7）：15-28．

[17] 郑蕾，雷浩．美国“实施课程调查”项目进展及运作机制——SEC项目主任约翰·史密森博士专访[J]．全球教育展望，2017，46（10）：11-23．

[18] 于涵，任子朝，陈昂，等．新高考数学科考核目标与考查要求研究[J]．课程·教材·教法，2018，38（6）：21-26．

[19] 任子朝，陈昂，黄熙彤，等．高考数学新题型试卷质量分析研究[J]．数学教育学报，2019，28（1）：1-7．

Research on Consistency between Mathematics Test Papers Volume Ⅰ of National College Entrance Examination and Mathematics Curriculum Standards——Sampling from 2007 to 2019

YI Xi-fan1, SUN Jia-ning1, ZHU Li-ming2

(1. School of Mathematics and Statistics, Northeast Normal University, Jilin Changchun 130024, China;2. Faculty of Education, Tangshan Normal University, Hebei Tangshan 063000, China)

In order to investigate the development of the new-type mathematics test papers (abbre. MTPs) under the background of the current College Entrance Examination reform (abbre. CEE), this paper, based on the SEC method (survey of enacted curriculum), puts forward a set of coding guidelines for mathematics curriculum standards (abbre. MCS) according to quantifying the two-level headers with their corresponding cognitive levels, and generates a pair of matrices representing coarse & fine scales respectively. Based on the work, the authors have quantified MTPs (Volume Ⅰ) of CEE from 2007 to 2019 and use the Person model testing to analyze the consistency between MTPs and MCS. The result finds that the interval range of the consistency coefficient values under the two scales of weight is different, but the variation trends are similar. It also shows that the distribution of the cognitive level, before and after the reform of the new college entrance examination, is different, indicating that recently the major adjustments have been made in the proposition link of Volume Ⅰ of CEE to adapt to the overall reform of the College Entrance Examination. These results can provide positive suggestions for the middle school mathematics teaching to meet CEE and scientific proposition of math questions for CEE and further implementation of the new curriculum standards as well.

new college entrance examination; college entrance examination paper; mathematics curriculum standards; consistency analysis; SEC method

G632.479

A

1004-9894（2020）06-0007-07

伊西凡，孙佳宁，朱立明．高考数学全国Ⅰ卷与课程标准的一致性研究——以2007—2019年为例[J]．数学教育学报，2020，29（6）：7-13．

2020-06-28

河南省教育科学“十三五”规划2018年度一般课题——新课程标准下高考数学试题SEC分析与预测研究（2018-JKGHYB-1591）

伊西凡（1995—），女，河南郑州人，硕士，主要从事数学教育研究．

[责任编校：周学智、陈隽]