基于APOS理论和RMI原则的二次函数图象平移教学实验研究

江春莲，胡 玲

基于APOS理论和RMI原则的二次函数图象平移教学实验研究

江春莲1，胡 玲2

（1．澳门大学 教育学院，澳门 999078；2．北京字节跳动有限公司上海分公司，上海 201100）

函数图象变换是中学数学中的重点和难点，尝试运用动态几何软件呈现二次函数图象平移过程中点的共同运动特点以促进学生的理解．采用准实验设计，实验包括6节课，其中4节用于教学实验，2节用于前测和后测．实验组（=23）的教学是基于APOS理论以及RMI原则设计的，并在DGS的支持下进行；而对照组（=22）则运用传统的教学，也无DGS的支持．结果表明：实验组的学生在点的平移、二次函数图象的平移以及复合函数和圆的平移等拓展领域均好于对照组．该实验设计可以扩展到三角函数图象变换教学．

APOS理论；关系—映射—反演原则（RMI原则）；函数；图象平移；多重表征

1 问题提出

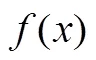
2 理论框架

关于二次函数图象平移的教学实验研究设计主要以杜宾斯基与其合作伙伴[3，9]提出的APOS理论为基础．该实验是在SSP的支持下进行的，SSP可以作为建立二次函数的代数表征和图象表征之间关联的媒介．然而，若要解决点的平移的代数表征和函数图象的代数表征之间的认知冲突，以及函数图象沿轴平移和沿轴平移的代数表征之间的认知冲突，需要运用关系—映像—反演（relationship mapping and inverse，简写为RMI）原则．图1展示了实验所涉及的4个方面之间的关系．下面将从APOS理论、函数的多元表征、DGS软件在函数教学中的应用和RMI原则4个方面作文献综述．

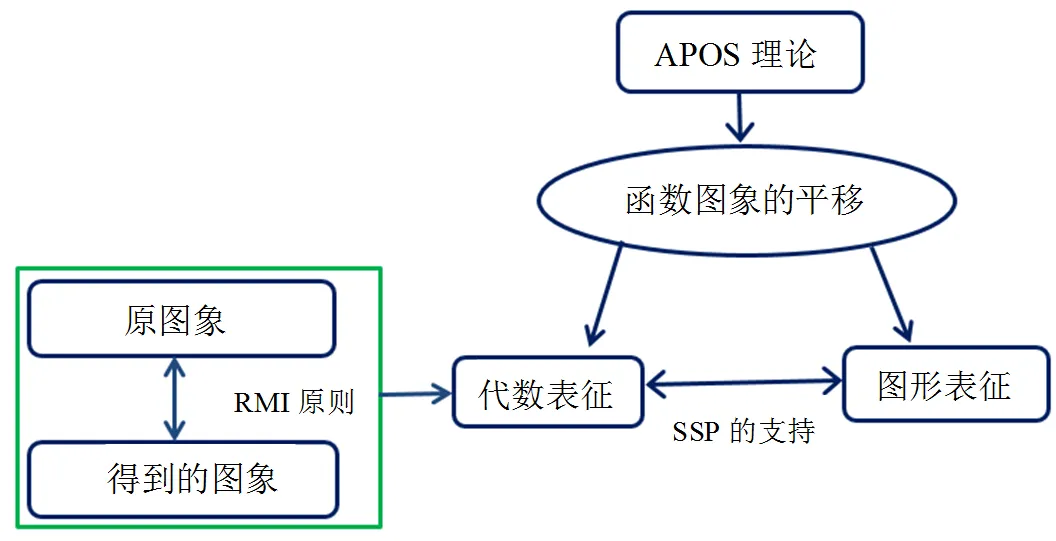
图1 “APOS理论”“多元表征”“SSP和RMI原则”之间的关系

2.1 “操作—过程—对象—图式”理论

在APOS理论中，当学生能够按照一套明确的指示对一个数学对象做变换时，就说他达到了操作水平．当学生不需要进行任何实际的操作就可以在脑海中进行整个操作或作反思时，就说学生将操作内化成了一个过程．如果学生意识到过程可以当作一个整体来把握并且可以对其实施更高级的操作时，学生的理解就达到了对象水平．此时，学生将内化形成的过程浓缩成一个对象．数学图式可以看作是当前的操作、过程和对象等概念和其它先前构建的图式所形成的连贯的整体[3，10-12]．图式的连贯性可通过学生能否用它来解决特定的数学问题的能力来确定[8]．杜宾斯基的图式概念源自皮亚杰[13]，皮亚杰指出学生学会了一个专题就意味着他能够解决和此专题相关的问题．

函数是中学数学的核心概念[2，14-15]．因此，关于函数概念的教与学的研究比较多[4，16]．杜宾斯基[13]认为，如果一个学生只能用数字代替公式中的字母，他对函数概念的理解处于操作阶段．如果他能内化这些操作并能将情境看作是对对象实施的一个操作，而该操作可以将一个函数对象变为另一个函数对象，他就能够协调函数过程及其图象，他对函数概念的理解就达到了过程阶段．反转函数的知求的过程以求得反函数可以看作是对函数的过程理解水平．当学生对函数的理解完成了内化—压缩过程并将其视为一个对象时（如可以解微分方程或建立不定积分），就可以看作达到了函数的对象理解水平．理解函数图象的平移和其它变换可以看作是对函数概念的过程和对象理解水平．

在运用APOS理论描述学生的建构过程时，研究者需要对学生要学习的概念从发生认识论的角度进行分解，生成一个假设的模型，以描述学生学习该数学概念可能需要建构的心理结构和机制[8]．结合RMI原则、多重表征理论和信息技术的整合理论，研究中的发生认识论的解构如下．

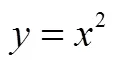
（3）对象．当学生能将二次函数的图象平移浓缩成一个整体，并迁移到一般的单变量函数时，更高层次的内化就出现了．RMI原则在这一过程中发挥了类似的作用．

（4）图式．主体可以运用函数图象平移的策略来解决其它涉及图形变换的问题，例如圆的平移或压缩等，形成连贯的知识体系．

2.2 函数的多重表征

日常用多重表征表示同一个数学概念，如函数，常用解析式、列表和图象等来表示．研究表明，与只通过单一表征（多数是代数符号表征）学习数学的学生相比，通过多重表征学习数学的学生通常对知识的记忆更长久，对知识的运用也更加高效[17]．多重表征可以促进学生对抽象的数学概念的理解[18-19]．中国的中学数学课程非常强调数形结合的思想方法，以帮助学生建立代数表征与图形表征之间的关联，并被广泛应用于数学教学和数学问题解决．

多重表征之间的转换可以帮助学生进行归纳．归纳能力是代数推理的一个标志，特别是在思维习惯上需要有重大突破时[6]．德雷福斯[18]提出归纳过程一般需要经历如下4个阶段：使用单个表征，平行地使用多重表征，在平行的多重表征之间建立联系，将不同表征整合在一起并能在彼此之间灵活进行转换．

多重表征的使用为抽象数学概念的学习提供了便利，然而不同表征之间的变换对学生来说，有时又会造成认知障碍[18-20]．借助现代资讯科技，可以帮助学生克服这些认知障碍．

一个函数可以用多种不同的表示形式，如语言、数字、图象和代数符号等形式[4]，它们呈现出函数的不同特征[21]．所以学生不仅需要运用多重表征来表示函数，还需要建立不同表征之间的关联，才能形成对函数的完整理解．大量研究表明多重表征的运用有助于函数的教学[11，22-24]，其不仅有助于学生理解观察到的现象与函数概念之间的联系，也有助于学生对函数概念的理解从操作水平提升到过程水平．

代数表征和图象表征之间的互动可以帮助学生在大脑中建构关于函数图象平移的知识．研究者试图以SSP为媒介去建立函数的多重表征之间的联系．在函数图象平移的过程，SSP可以动态地呈现原图象上的点如何移到新的函数图象上，这种动态表征有助于建立原函数图象和新函数图象之间的联系．以SSP为媒介的多重表征也有助于学生通过同时显示的代数表征和图象表征的变化归纳函数图象平移的普遍规律．DGS软件（包括几何画板GSP、SSP等）能动态地、灵活地处理不同表征形式的函数，例如表格、图象、解析式等形式[25]，其提供的多重表征及其之间的动态变换可以丰富学生对数学对象和过程的理解．

2.3 动态几何软件

当前，可用于数学教学的软件有很多，如可用于代数教学的软件有计算机代数系统（CAS）、SimCalc、动态几何软件（包括GSP、SSP等）以及其它相似的软件．与传统的代数教学相比，这些软件提供的环境通常具备如下5个特点：（1）它提供了支持性的、丰富的问题解决环境；（2）减少了用于技能训练的时间，因此学生将更多的时间和精力用于发展概念性理解；（3）技术的广泛应用；（4）提高了学生的学习动机；（5）促进了与现实世界问题的联系[6，23-24，26-28]．CAS软件建立了图象、数字和符号运算之间的多重联系，这使得老师和学生可以用它来解决各种现实世界问题[29]．如在SimCalc中，使用者能调查和研究模拟的现象，探索与运动相关的数学概念[30]．

自20世纪80年代第一个DGS软件GSP问世以来，动态几何的教育价值很快得到世界各国数学教育工作者的肯定，DGS软件在数学教学中的运用也一直是一项热门的研究课题．在传统的数学课堂里，DGS软件通常用作教学的辅助手段．如中国的数学教师在制作课件时，常使用SSP来帮助学生探究几何对象之间的关系，掌握它们的本质属性[31-32]．在创新的数学课堂里，DGS则通常用作学生的学习工具．这些工具给学生提供了独立探索数学思想、验证假设和分析例子的机会．当学生的学习变为主动时，老师的角色则变成了学习的指导者和促进者．这种全新的师生关系提高了学习效率并且促进了师生之间在情感和学术上的交流[27]．近来有许多研究关注到DGS软件提供的动态行为（如拖曳），特别是学生运用DGS软件动态行为的策略可以促进他们建构抽象的数学概念[24，28，33-35]．

计算机软件（如DGS）如果运用得当，可以促进学生的纵向发展（从操作到对象水平的发展）和横向发展（不同表征之间关联的建立）[9，12，18，23-24，36]．计算机软件可以用具体的形式表示抽象的概念，进而简化学生学习的纵向发展过程．它还可以让学生在对一种表征进行操作的过程中研究另一个表征的相应变化，进而帮助学生建立多重表征之间的联系[36-37]．SSP软件主要起到辅助教学的作用，其主要有两个作用，一是同步显示多重表征，帮助学生建立它们之间的关系；二是在函数图象平移的过程中追踪对应点的变化．图2和图3分别展示了原函数图象上的每一点如何一致地沿轴和轴平移到新的函数图象上．与此同时，希望SSP的运用能激发学生对数学学习的兴趣．

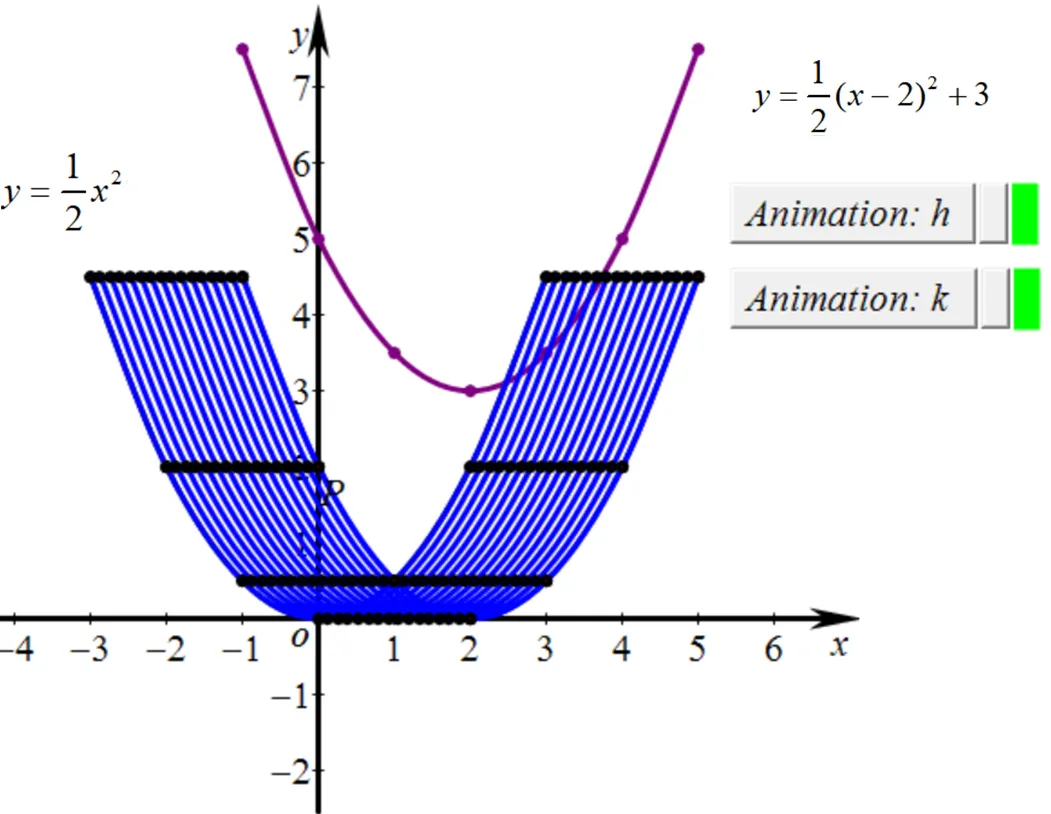
图2 原图象上的每一点以相同的方式沿x轴平移

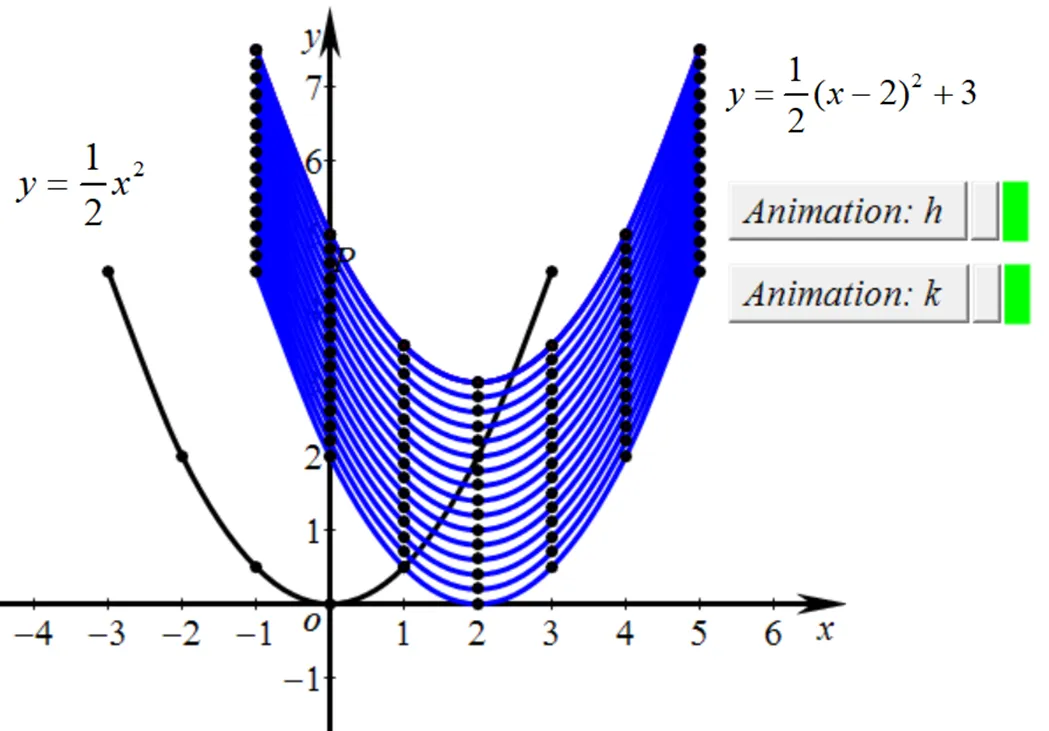
图3 原图象上的每一点以相同的方式沿y轴平移

学生可以通过追踪移动图象上的点，看到所有的点以相同的方式移动，来理解函数图象的平移过程．必须注意到，二次函数沿轴的平移看起来比沿轴的平移更明显．在图3中，两个终点所走的距离似乎比最低点所走过的距离要短，这里有个视觉差．这个问题后面还会作进一步探讨．

2.4 两个认知冲突

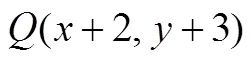
2.5 关系—映射—反演原则

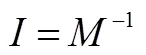
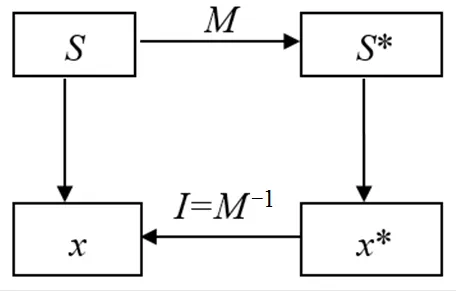
图4 RMI原则

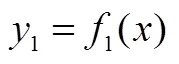
3 研究问题

研究旨在回答这样一个研究问题：“与传统教学相比，基于APOS理论和RMI原则设计的、在DGS支持下的一元二次函数图象的教学能否更好地促进学生对函数图象平移的理解？”对应的研究假设是：与传统教学相比，基于APOS理论和RMI原则设计的、在DGS的支持下的一元二次函数图象的教学能更好地促进学生对函数图象平移的理解．

4 研究方法

采用准实验设计，实验时间跨两周，总共6节课，其中4节用于教学，前后两节分别用于前测和后测．实验组学生接受SSP支持下的实验教学，对照组则采用传统的教学，不使用任何DGS软件．

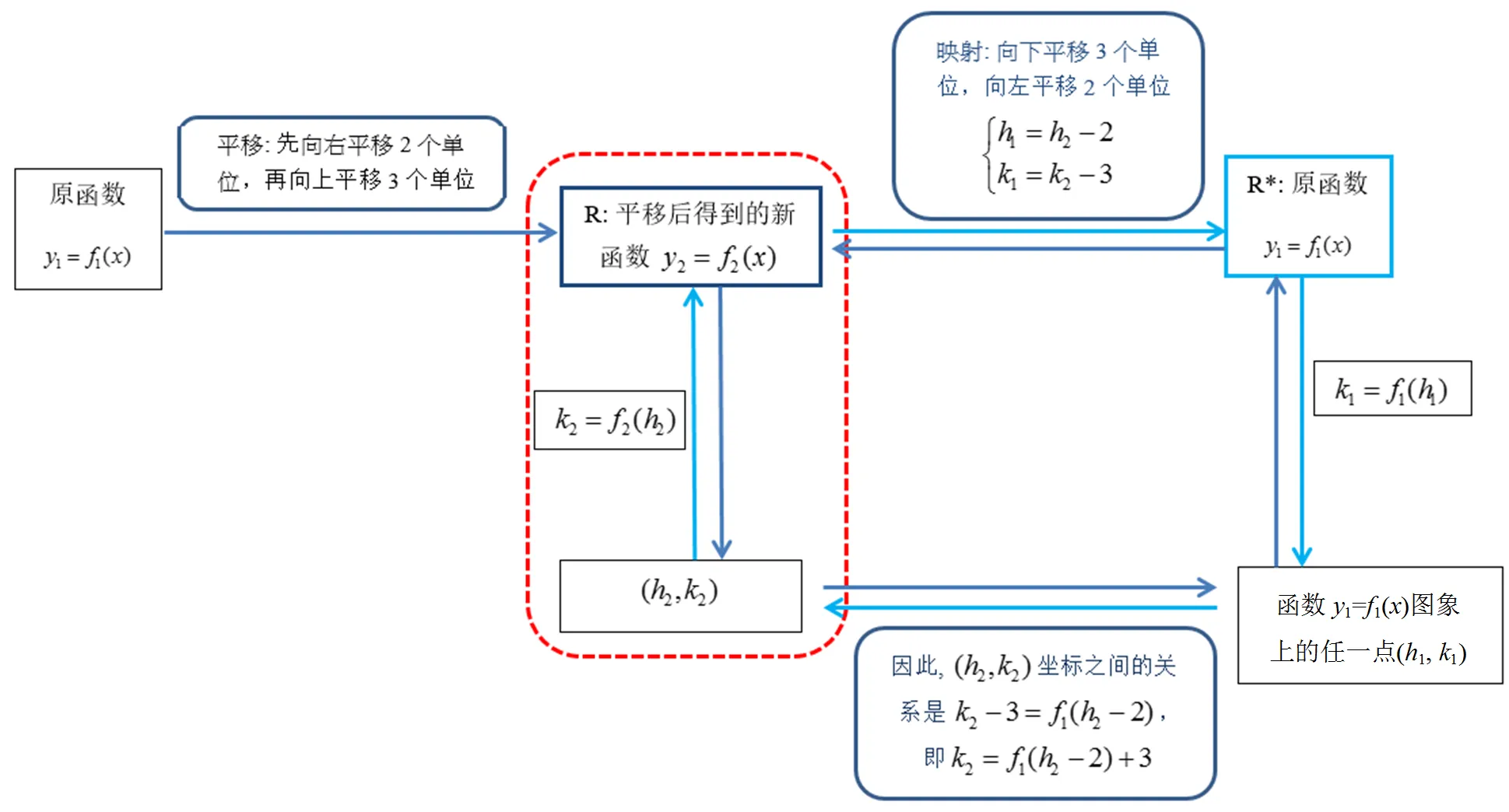
图5 RMI原则在函数图象平移中的应用

实验对象是来自西安市某校两个十年级的班级共45名学生．其中实验组学生23名（女生8名，男生15名）；对照组学生22名（女生7名，男生15名）．两班学生男女比例比较接近．实验组和对照组的教学均由原班数学老师实施，是同一位老师．

实验措施：在教学实验进行之前，两个班的实验对象已在九年级时学习过二次函数并且知道二次函数的基本特点．他们也学习过二次函数图象平移的基本规则，即左加右减，上加下减．实验组的教学主要是基于前面提到的发生认识论视角的分解而设计的，并且要先介绍3个背景专题．实验组的教学从点的平移开始，通过二次函数的图象平移，到单变量函数的图象平移．在SSP的支持下，实验组的教学还侧重于展示平移前后两个函数图象上对应坐标点之间的关系以及函数的图形表征和代数表征之间的关联．四节课的教学涵盖了如下7个专题．

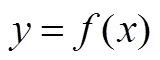
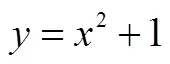
（3）点的平移．这部分同样借助于SSP的支持，涉及坐标平面R2上点的平移以及平移过程中的多重表征．

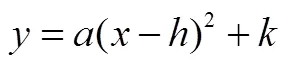
（5）二次函数图象的平移1（顶点法）．基于顶点的平移，使用RMI原则将原函数和平移后得到的函数关联起来．

（6）二次函数图象的平移2（任意点）．由二次函数上特殊的点（如顶点）扩展至二次函数图象上的任意点，在SSP的帮助下，学生会发现不仅是二次函数图象的顶点，该图象上的任意点都以相同的方式平移．学生可能也会认为函数图象上的所有点跟着顶点做相同的平移．

（7）单变量函数的图象平移（任意点）．第六部分可以作为这里的引入部分．在这里，学生可以发现第六部分的规则适用于任何单变量函数图象的平移．

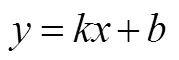
数据分析．对于填空题，使用0—1评分法．还确定了参与者可能达到的APOS的阶段．处于操作前阶段的学生无法在所有涉及操作阶段的题目上得到正确的答案．而处于操作阶段的学生应该在所有涉及操作阶段的问题上得到正确的答案．处于过程阶段的学生应该在所有涉及操作和过程阶段的问题上得到正确答案．处于对象阶段的学生应该在操作、过程和对象阶段的所有问题上得到正确答案．处于图式阶段的学生应该能正确回答所有问题．

通过检验比较实验组和对照组学生的成绩增长是否有差异．

5 实验结果

实验得到的Cronbach’s系数是0.84，所以从统计意义上来说，测试是可信的．下面将首先报告两组学生的总分，然后再呈现达到操作、过程、对象和图式等阶段的学生的百分比，以比较两组学生的表现差异．

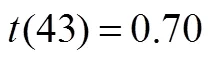
表1 实验组和对照组学生在前测和后测的原始总分的 均值（标准化的）和标准差

注：前测满分是25分，后测满分是34分；前测和后测标准化后的范围是[0, 100]；**<0.01．

表2展示了在不同APOS阶段学生的百分比．对照组的学生在前测和后测中的百分比没有太大差异．在前测中，实验组的学生在操作阶段的百分比高于对照组，而在其余3个阶段，实验组和对照组学生在百分比之间没有多大差异．然而，在后测中，实验组的学生达到图式阶段所占的百分比远高于对照组，而且实验组的学生在操作阶段所占的百分比也远低于对照组．尽管在过程和对象阶段，实验组和对照组学生的百分比之间没有较明显的差异，实验组学生在后测中到达对象阶段和图式阶段所占的百分比均有提升．与此同时，实验组的学生在后测中达到过程阶段的百分比和图式阶段的百分比均高于前测中的对应百分比，相应地，实验组学生在后测中处于操作阶段的百分比较明显地低于其在前测中的百分比．

表2 学生在不同APOS阶段所占的百分比

这些结果表明，研究设计有助于实验组学生在函数图象平移的理解方面从操作阶段向图式阶段提升．特别地，更多的学生能够在脑中建构二次函数图象平移的意象，并运用这一策略解决其它数学图形的平移问题．SSP的使用不仅可以促进学生的理解从操作阶段向对象阶段提升[3，9，11]，也可以帮助学生从对象阶段向图式阶段提升．他们可以扩展函数图象平移的策略来解决解析几何中的图形（如圆）平移问题．RMI原则的使用有助于学生将这种问题解决的方法融会贯通．

6 讨论

研究表明：基于APOS理论和RMI原则设计的、在DGS支持下的教学可以帮助实验组学生形成对函数图象平移的更好理解．同时，实验组学生在拓展问题上的突出表现表明：该教学设计可以帮助实验组学生完成从操作阶段向图式阶段的过渡．

之前的研究表明，大多数学生对函数概念的理解停留在操作阶段，而没能达到APOS理论中更高的水平[4]．研究结果表明：好的教学设计是可以帮助学生从操作阶段提升到过程阶段，甚至更高的阶段．怎样达成这个目标呢？研究中试图去跟踪一些点以帮助学生看到原函数和新获得的函数图象上的点是如何关联的．这种跟踪也可以让学生看到所有的点以相同的方式移动，因此可以帮助学生看到原函数图象上的点和新获得函数图象上的点之间的一一对应关系．DGS软件所提供的跟踪功能的创造性运用，帮助实验组学生看到二次函数图象的平移，不仅是基于相应点的平移，更重要的是均与顶点做相同的平移．点的跟踪给学生提供了一个将操作内化的机会．研究者观察到大多数教师只是追踪一个运动着的函数图象，希望学生能看到原函数和新获得函数之间的关系．然而，如果不基于点的平移，学生将很难看到两个图象之间的关联．

当然，跟踪的运用只能“显示”平移对图象的影响，包括对图象表征和代数表征的影响．DGS提供了德雷福斯所建议的可平行使用多个表征的平台．然而，它并不能解释点的平移和函数图象平移之间的认知冲突，这时RMI原则的使用发挥了更重要的作用．实验中RMI原则的运用不仅能帮助学生解决认知冲突，还能将这一策略推广到解决解析几何中一般的图形平移问题．同时，RMI原则的运用也能避免传统教学方法给学生造成的困惑，因此也可能会降低实验组学生的认知负荷．

7 启示

研究表明：点的平移是学生理解函数图象平移的基础．不幸的是，在20世纪90年代，教学中已经将点的平移从高中数学课程中删除．强烈建议重新将这一内容加入高中数学课程，为学生深刻理解函数图象的平移和变换打好基础．

研究主要关注二次函数图象沿两个坐标轴的平移，该设计思想同样可以用于其它函数（如三角函数）及其包括平移在内的图象变换．同样地，点的坐标变换也是三角函数图象变换的基础．因此，点的坐标变换也应被纳入高中数学课程之中，并放在三角函数图象变换之前．像SSP这样的DGS软件所提供的跟踪功能是一种很强大的工具，它可以显示两个相互关联的图象上的点与点之间关系，帮助学生建立图象表征和代数表征之间的关联．

不可避免，研究也受到实验条件的限制．首先样本太小，需要有更大样本的研究．其次，在前测和后测中需要加入更多的题目，以保证在APOS理论的每个阶段中至少有3道题目．最后，在研究中，SSP用来说明原函数图象和平移后的函数图象之间的关系．这个工具也可以教给学生，让他们自己去探索一组函数图象之间的关联，以及代数和解析几何中其它相似的专题．

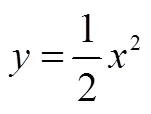
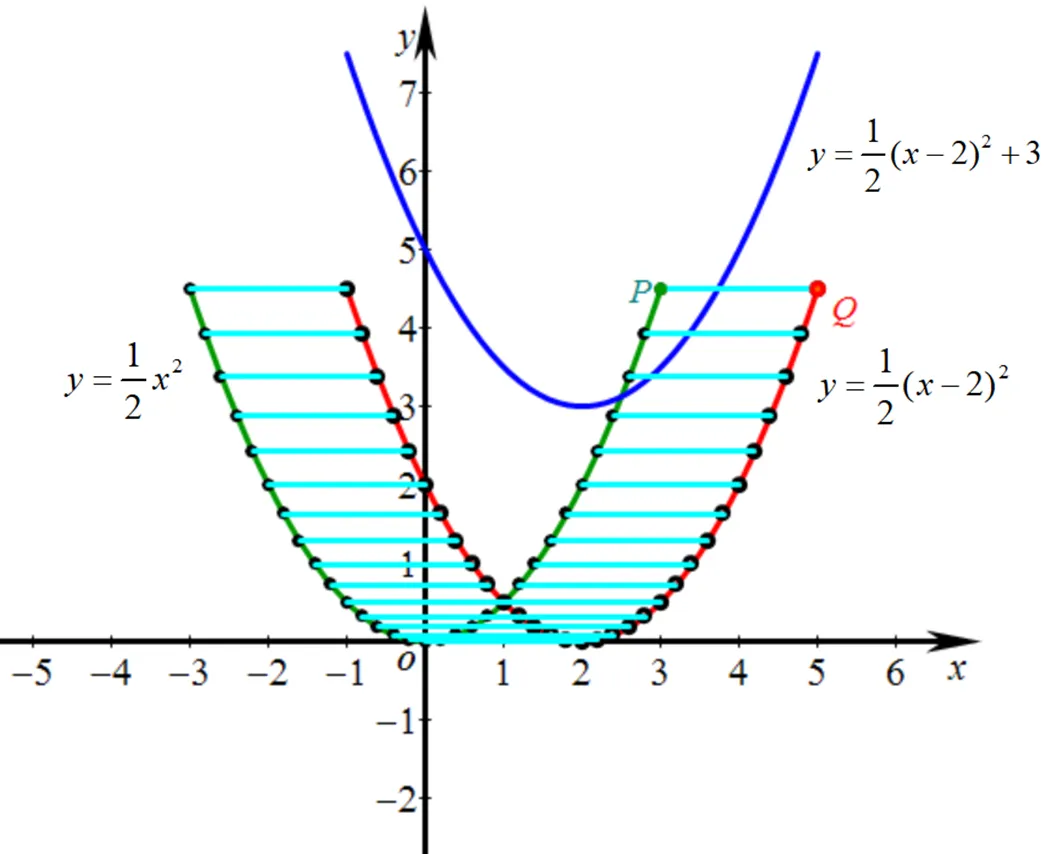
图6 函数和图象之间的关系

图7 函数和图象间的关系

8 结论

简而言之，实验成功地将多种数学教育理论（APOS理论、RMI原则、表征理论等）综合在一起解决学生在学习二次函数图象平移中的困难．对数学教育的贡献在于它不仅指出了学生在学习二次函数图象平移时可能遇到的认知障碍，还设计了一个教学计划以帮助学生克服可能存在的障碍．先前的研究表明学生们对于函数概念的理解常限于操作阶段而不能达至APOS理论中更高的层次[4]，这里通过DGS环境的支持，结合RMI原则的解释所设计的教学可以提升学生的理解．DGS软件清晰地展示了原函数图象上的每个点是如何移动到平移后的图象上的对应点．除此之外，DGS软件清晰地展现了所有的点都在以相同的方式移动，这有助于学生对操作阶段进行内化，从而进入更高层次的过程阶段．而对二次函数图象平移形成较好的理解，必将为今后微积分和大学数学中复合函数的研究奠定坚实的基础．

[1] 中华人民共和国教育部．全日制义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：62．

[2] Common Core State Standards Initiative. Common Core State Standards for mathematics [EB/OL]. (2010-06-06) [2020-04-01]. http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf.

[3] DUBINSKY E. Reflective abstraction in advanced mathematical thinking [M] // TALL D. Advanced mathematical thinking. Dordrecht: Kluwer, 1991: 95-123.

[4] DUBINSKY E, WILSON R T. High school students’ understanding of the function concept [J]. Journal of Mathematical Behavior, 2013 (32): 83-101.

[5] MEVARECH Z R, KRAMARSKY B. From verbal descriptions to graphic representations: Stability and change in students’ alternative conceptions [J]. Educational Studies in Mathematics, 1997 (32): 229-263.

[6] YERUSHALMY M. Designing representations: Reasoning about functions of two variables [J]. Journal for Research in Mathematics Education, 1997 (28): 431-466.

[7] SFARD A. On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin [J]. Educational Studies in Mathematics, 1991 (22): 1-36.

[8] ARNON I, COTTRILL J, DUBINSKY E, et al. APOS theory: A framework for research and curriculum development in mathematics education [M]. New York: Springer, 2014: 112.

[9] DOORMAN M, DRIJVERS P, GRAVEMEIJER K, et al. Tool use and the development of the function concept: From repeated calculations to functional thinking [J]. International Journal of Science and Mathematics Education, 2012 (10): 1 243-1 267.

[10] BAKER B, COOLEY L, TRIGUEROS M. The schema triad: A calculus example [J]. Journal for Research in Mathematics Education, 2000 (31): 557-578.

[11] BREIDENBACH D, DUBINSKY E, HAWKS J, et al. Development of the process conception of function [J]. Educational Studies in Mathematics, 1992 (23): 247-285.

[12]  TRIGUEROS M, MARTINEZ-PLANELL R. Geometrical representations in the learning of two-variable functions [J]. Educational Studies in Mathematics, 2010 (73): 3-19.

[13]  PIAGET J. Piaget’s theory [M] // MUSSEN P H. The process of child development. New York: Jason Aronson, 1975: 164-212.

[14]  National Council of Teachers of Mathematics. Curriculum and evaluation standards for school mathematics [M]. Reston, VA: Author, 1989: 98, 154.

[15]  National Council of Teachers of Mathematics. Curriculum and evaluation standards for school mathematics [M]. Reston, VA: Author, 2000: 15.

[16]  AYERS T, DAVIS G, DUBINSKY E, et al. Computer experiences in learning composition of functions [J]. Journal for Research in Mathematics Education, 1988, 19 (3): 243-259.

[17]  HUNTLEY M A, RASMUSSEN C L, VILLARUBI R S, et al. Effects of standards-based mathematics education: A study of the core-plus mathematics project algebra and functions strand [J]. Journal for Research in Mathematics Education, 2000 (31): 328-361.

[18]  DREYFUS T. Advanced mathematical thinking processes [M] // TALL D. Advanced mathematical thinking. Dordrecht: Kluwer, 1991: 25-40.

[19]  VINNER S, DREYBUS T. Images and definitions of the concept of function [J]. Journal for Research in Mathematics Education, 1989 (20): 356-366.

[20]  THOMPSON P W. Students, functions, and the undergraduate curriculum [M] // DUBINSKY E, SCHOENFELD A H, KAPUT J J. Research in collegiate mathematics education. Providence, RI: American Mathematical Society, 1994: 21-44.

[21]  ELIA I, PANAOURA A, ERACLEOUS A, et al. Relations between secondary pupils’ conceptions about functions and problem solving in different representations [J]. International Journal of Science and Mathematics Education, 2007 (5): 533-556.

[22]  MARTINEZ-PLANELL R, TRIGUEROS G M. Students’ ideas on functions of two variables: Domain, range, and representations [C] // SWARS S L, STINSON D W, LEMONS-SMITH S. Proceedings of the 31st annual meeting of the North American chapter of the international group for the psychology of mathematics education. Atlanta, GA: Georgia State University, 2009: 73-80.

[23]  YERUSHALMY M. Problem solving strategies and mathematical resources: A longitudinal view on problem solving in a function based approach to algebra [J]. Educational Studies in Mathematics, 2000 (43): 125-147.

[24]  YERUSHALMY M. Slower algebra students meet faster tools: Solving algebra word problems with graphing software [J]. Journal for Research in Mathematics Education, 2006 (37): 356-387.

[25]  PONTE J P. The history of the concept of function and some educational implications [J]. The Mathematics Educator, 1992, 3 (2): 3-8.

[26]  BEN-CHAIM D, LAPPAN G, HOUANG R. The role of visualization in the middle school mathematics curriculum [J]. Focus on Learning Problems in Mathematics, 1989 (11): 49-60.

[27]  O’CALLAGHAN B C. Computer-intensive algebra and students’ conceptual knowledge of functions [J]. Journal for Research in Mathematics Education, 1998 (29): 21-40.

[28] TALMON V, YERUSHALMY M. Understanding dynamic behavior: Parent-child relations in dynamic geometry environments [J]. Educational Studies in Mathematics, 2004 (57): 91-119.

[29]  HEID M K, EDWARDS M T. Computer algebra systems: Revolution or retrofit for today’s mathematics classroom [J]. Theory Into Practice, 2001 (40): 128-136.

[30] MORENO-ARMELLA L, HEGEDUS S J, KAPUT J J. From static to dynamic mathematics: Historical and representational perspectives [J]. Educational Studies in Mathematics, 2008 (68): 99-111.

[31] 张景中，江春莲，彭翕成．《动态几何》课程的开设在数学教与学中的价值[J]．数学教育学报，2017，26（3）：1-5．

[32] 张景中，江春莲，彭翕成．基于《超级画板》开设《动态几何》课程的实践与思考[J]．数学教育学报，2018，27（5）：1-5．

[33]  HOLLEBRANDS K F. The role of a dynamic software program for geometry in the strategies high school mathematics students employ [J]. Journal for Research in Mathematics Education, 2007, 38 (2): 164-192.

[34]  LEUNG A, BACCAGLINI-FRANK A, MARIOTTI M A. Discernment of invariants in dynamic geometry environments [J]. Educational Studies in Mathematics, 2013 (84): 439-460.

[35]  LEUNG A, LEE A M S. Students’ geometrical perceptions on a task-based dynamic geometry platform [J]. Educational Studies in Mathematics, 2013 (82): 361-377.

[36]  TALL D. Computer environments for the learning of mathematics [M] // BIEHLER R, SCHOLZ R, STÄßER R, et al. Didactics of mathematics as a scientific discipline. Netherlands: Kluwer Academic Publishers, 1994: 189-199.

[37]  DREYFUS T. The role of cognitive tools in mathematics education [M] // BIEHLER R, SCHOLZ R, STÄßER R, et al. Didactics of mathematics as a scientific discipline. Netherlands: Kluwer Academic Publishers, 1994: 201-211.

[38] 徐利治．数学方法论选讲[M]．武汉：华中理工大学出版社，1988：24-29．

Teaching Graph Translation of Quadratic Functions Based on APOS Theory and RMI Principle: A Quasi- Experimental Study

JIANG Chun-lian1, HU Ling2

(1. Faculty of Education, University of Macau, Macao 999078, China;2. Shanghai Branch, Beijing Bytedance Limited Cooperation, Shanghai 201100, China)

Graph translation of functions is an important but difficult topic in high school mathematics. This study attempts to facilitate students’ understanding of graph translation of quadratic functions in a dynamic-geometry-software (DGS) supported environment. A quasi-experimental study design was used. This teaching experiment was carried out in two weeks including six lessons, four of which were used for teaching and two for pre- and post-tests. The experimental group (=23) received an instruction based on Action-Process-Object-Schema (APOS) theory and Relationship-Mapping-Inversion (RMI) principle in a DGS supported environment. The control group (=22) followed the traditional instruction without using any DGS. The comparison between students’ performance in the pre- and post-tests indicates that the experimental group outperformed the control group not only in items of point translations and graph translation of quadratic functions, but also in items in an extended area including complex functions and circles. This quasi-experimental design can be extended to the teaching of graph transformation of trigonometrical functions as well as geometrical shapes in 2-D and 3-D coordinate systems.

APOS theory; Relationship-Mapping-Inversion (RMI) principle; function; graph translation; multiple representations

G632.0

A

1004-9894（2020）06-0032-08

江春莲，胡玲．基于APOS理论和RMI原则的二次函数图象平移教学实验研究[J]．数学教育学报，2020，29（6）：32-39．

2020-08-18

澳门大学研究基金项目——高中生函数学习路径分析（MYRG2020-00277-FED）

江春莲（1971—），女，湖北武汉人，助理教授，主要从事数学问题解决、数学问题提出、数学考试评价、数学教育技术、数学奥林匹克研究．

[责任编校：周学智、陈汉君]