基于共同趋势提取的多维有序聚类方法

何韩吉，邓光明，b

(桂林理工大学 a.理学院；b.应用统计研究所，广西 桂林 541004)

一、引 言

样本的有序聚类，是对有序样本在样本次序相关的前提下进行聚类的方法。随着数据维度的增加，有序聚类方法在多维情形下已经不再适用[1-3]。对于多维有序聚类的处理有两种方式：一是直接构建多维有序聚类方法，如程乾生引入加权思想，用权函数和广义相关系数度量多维序列之间的差异度[4]；二是通过降维或信息提取来处理多维数据，如张彦周构建了有序聚类投影寻踪模型，并应用于郑州市房地产评价，发现结果受到离群值的影响较大[5]。杨毅等通过主成分分析处理多维数据，解决有序面板数据时间尺度的维度问题[6]。在第二种方法中，由于受到多维数据离群值及冗余信息的影响，信息提取的一维有序数据不能完全体现数据的发展趋势。此类方法无法获得合理的多维有序聚类结果，需要对离群值及冗余信息进行处理。

现有的基于信息提取的多维有序聚类分析主要存在以下问题：一是在多维有序数据的各个指标之间一般都存在相关性的前提下，不考虑数据的主要趋势，直接进行有序聚类无法获得代表整体趋势的结果；二是利用主成分或投影寻踪等降维方法不能解决离群值和冗余信息的影响；三是多维时间序列离群值检测方法无法直接应用于多维有序数据的变量处理上。本文通过对多维序列样本进行动态聚类提取共同趋势，用共同趋势进行有序聚类，不仅可以剔除离群值和冗余信息的影响，而且也提取了多维有序数据的主要趋势，使有序聚类结果符合多维数据总体的趋势情况。

二、多维有序聚类方法

(一)传统主成分多维有序聚类

主成分方法是基于降维的思想，保留主要信息不丢失的基础上对数据进行压缩的方法[12]。此方法广泛应用于多维数据的处理当中，自然可以解决多维时间序列数据的信息提取问题，从而有效解决多维有序聚类。具体做法是通过主成分降维完成对多维有序数据的信息提取，对主成分得分进行有序聚类。

首先，X={x1，x2，…，xp}′是p个样本的多维有序数据，每个样本是有n个时序的有序数据，即行方向上为时序，列方向上为样本，且x1，x2，…，xp相互之间具有较强的相关性。主成分分析有效与否的关键在于协方差矩阵的稳健性。可以看出，协方差的计算与样本的均值密切相关，从而能够对特征值和特征向量产生影响。如果对样本的均值影响不大，那么就不会影响主成分分析的结果。

Cov(x，y)=E[(x-E(x))(y-E(y))]

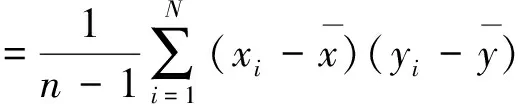
(2)

Cov(X)=

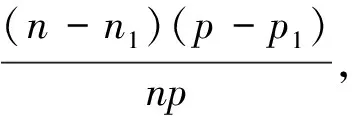
在协方差矩阵未发生较大变化的情况下，没有对主成分载荷矩阵的结果产生影响，但在依据载荷矩阵计算主成分得分时，变化不明显的权重将离群值按照相同比例相加。与没有离群值的结果相比，在某些时序点上出现了较大的差异，而将这一错误序列进行有序聚类自然无法得到可靠有效的聚类结果。

在前面提到，样本中可能存在一些时点上有不同的变化趋势，因此在时序维度上块状分布的离群值不会产生很大的影响。在样本维度上，离群的样本比例越高对主成分得分的影响越大。在这样的情况之下，主成分得分不能代表整体趋势，主成分降维的方法不适合处理存在离群值的多维有序数据。

(二)基于共同趋势提取的稳健多维有序聚类

基于以上讨论，主成分方法无法改变时序维度上主成分得分的问题，离群值对聚类结果的影响很大。而从样本维度来看，存在几种不同的变化趋势，需要考虑哪一类变化趋势占据主导地位。基于这样的考虑，本文提出基于共同趋势提取的多维有序聚类方法。主要算法步骤如下：

1.数据归一化处理

首先，对数据进行归一化处理，消除各变量的量纲对分析结果的影响。设多维有序聚类的样本集为{xij|i=1，2，…，n;j=1，2，…，p}，其中xij表示第i个样本中第j个变量的值，时序为n个，样本数有p个。 计算方法如下：

正向数据：

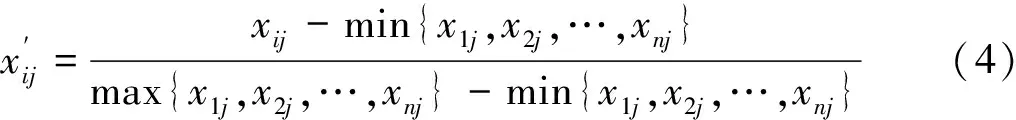
负向数据：

2.提取共同趋势

提取多维有序数据的共同趋势，采用k-means动态聚类迭代算法，基本思想为：将数据分成k组并使得样本到其指定的聚类中心的平方的总和为最小。具体的计算步骤如下：

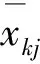
k*=arg max(ni/n)

(7)

由于聚类是对原始数据的变量维度聚类，因此即使离群值很少，根据k-means聚类原理，无离群值序列趋势相似，存在一个聚类中心；同时，离群值一般在正常数值的3倍标准差之外，导致存在离群值序列的离差平方和与无离群值序列的离差平方和差异较大，所以存在离群值的序列能够形成另外的聚类中心。与传统主成分相比，传统主成分方法对离群值的抗干扰性差，而本文所提出的方法则不会出现误判的情况。

3.对共同趋势进行有序聚类

三、数值模拟

下面证明本文所提出的方法与传统的主成分降维方法相比，在多维有序聚类的应用中更加稳健，对离群值的抵御能力更强。模拟数据是时序大小为n=40，样本数p=20的多维有序数据，并且具备以下两个特点：序列之间存在较强的相关性，趋势变化相似和离群值呈现块状分布特征。

(一)模拟数据生成

1.生成基本序列

为了获得强相关性的有序多维数据，需要生成一维有序基本数据x1，主要分为四段，第一段为1到10等差为1的等差序列；第二段为10到11等差为0.1的等差序列；第三段为10到6等差为-1的等差序列；第四段分为两部分，第一部分为 6.5，6.4，6.3，7，8，第二部分为8.1到8.18等差为0.01的等差序列。具体趋势见图1，可见时序大小为40，大致存在两个高峰和两个低谷段，满足趋势性。

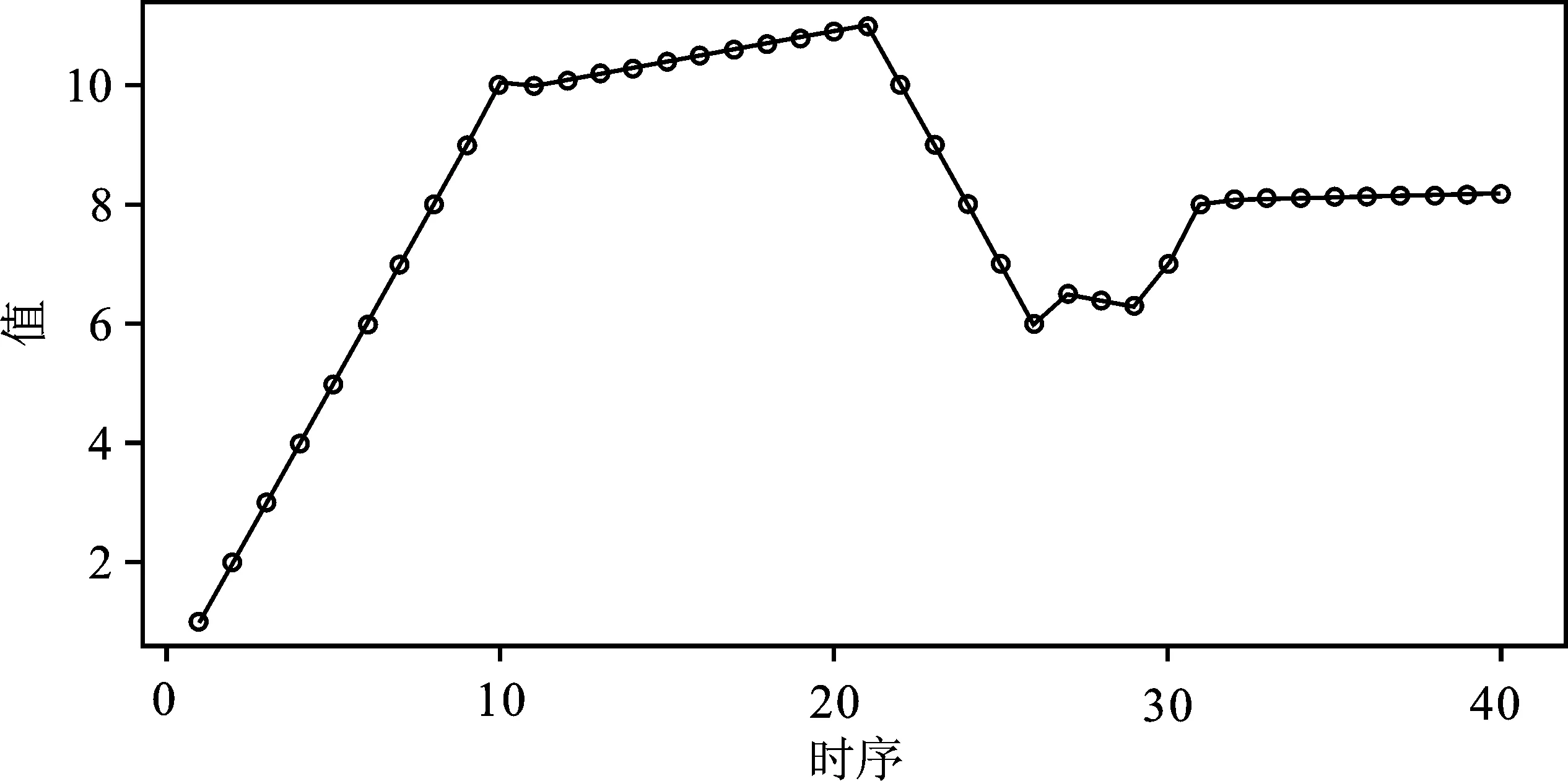
图1 一维有序样本数据折线图

2.生成有序多维数据

对基本数据进行20次平移，保持共同趋势性不变，获得强相关性；在所有序列上增加噪声，增强一般性：

x1+αi，αi～N(i-0.5，1)，i=1，2，…，n

生成有序多维数据X=(x1，x2，…，x20)′。从图2的部分序列折线图可以看到，5条序列的整体发展趋势趋同，满足序列之间存在较强的相关性。

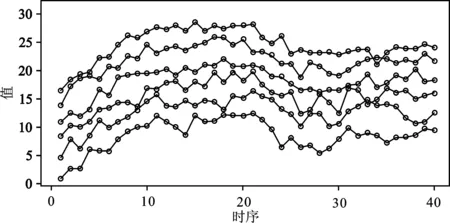
图2 同趋势有序多维数据(部分)折线图

3.添加离群值

在样本维度随机选择6组变量，随机选择了第1，6，8，15，16，17个变量作为离群值变量。在时序维度选择这些变量的第36～40个时序上插入离群值εj，εj～N(8，1)，j=1，2，…，0.2×n，离群值满足块状分布的特征。此外，在样本维度上存在离群的样本有30%，在时序维度上存在离群的时序点有12.5%，离群值比例仅为3.75%，但是由于其特殊的结构，不易改变协方差矩阵，而在样本维度的加权计算则会使第36～40个时序值偏高，从而导致了降维的失败。进一步，将以上6组变量与第2个变量对比，观察离群值加入之后的效果，见图3，实线为无离群值样本，虚线为含有离群值的样本，可见在第36～40个时序上，它们是显著不同的。

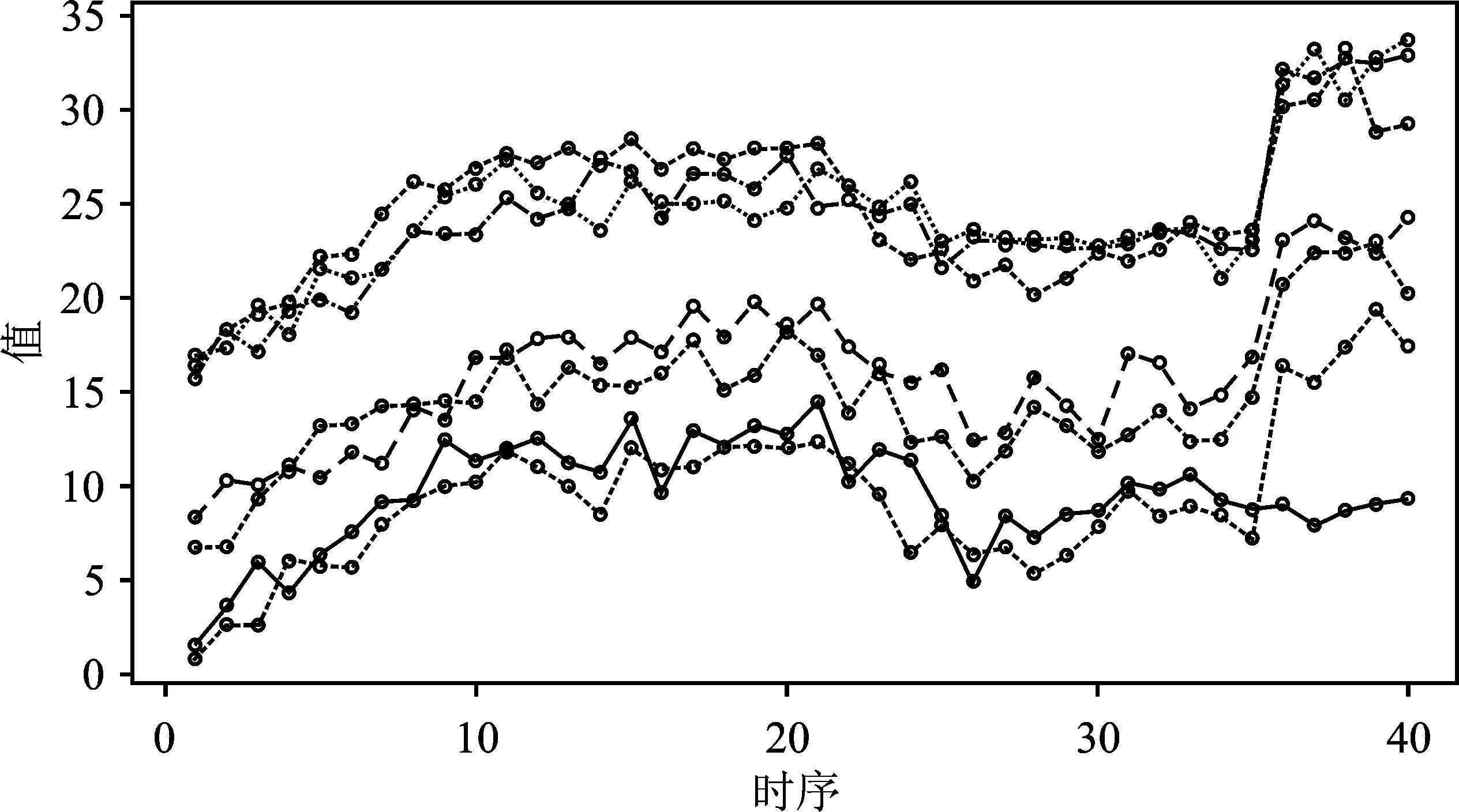
图3 离群有序多维数据(部分)折线图

(二)有序聚类的结果比较

对多维有序数据X进行共同趋势的提取，k-means 聚类的数目为2。相应的聚类中心代表了不同的趋势，提取了含有离群值和无离群值的两种趋势；再通过聚类结果进行投票，聚类数量较多的趋势作为共同趋势进行提取。趋势2有14个样本，为共同趋势，与上文中未添加离群值的序列比较，趋势相似。趋势1有6个样本，为异常趋势，与上文添加离群值的结果比较，趋势相似。比较结果说明了k-means 聚类方法对趋势提取的准确，详见图4。

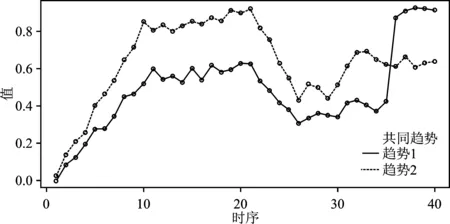
图4 有序多维数据共同趋势折线图

通过共同趋势提取，我们将多维有序数据转化为一维有序数据来进行处理。在做有序聚类之前，对降维的数据与共同趋势进行比较，发现传统主成分方法对离群值非常敏感，在第36～40个序列上与不存在离群值的主成分序列显著不同。而本文所提出的共同趋势提取方法与不存在离群值的传统主成分方法趋势一致，详见图5。

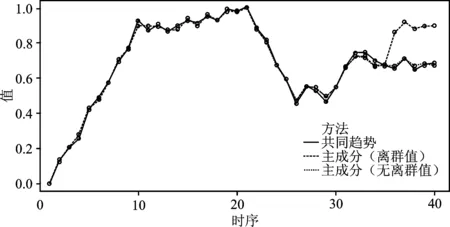
图5 不同方法和情况下转换的一维有序数据对比

进一步，通过观察序列图像的趋势，将数据聚为4类较为合适。从表1中明显看到所担忧的离群值影响了有序聚类的结果，当存在离群值时，传统主成分方法会导致对离群值的误判，将第36～40个序列点聚为一类。但是，此时离群值仅仅占到了数据的3.75%，可见传统主成分方法对离群值相当敏感。而本文所提出的共同趋势提取方法与无离群值时传统主成分的结果相同，并没有受到离群值的影响，聚类结果符合多维有序数据的整体变化趋势。

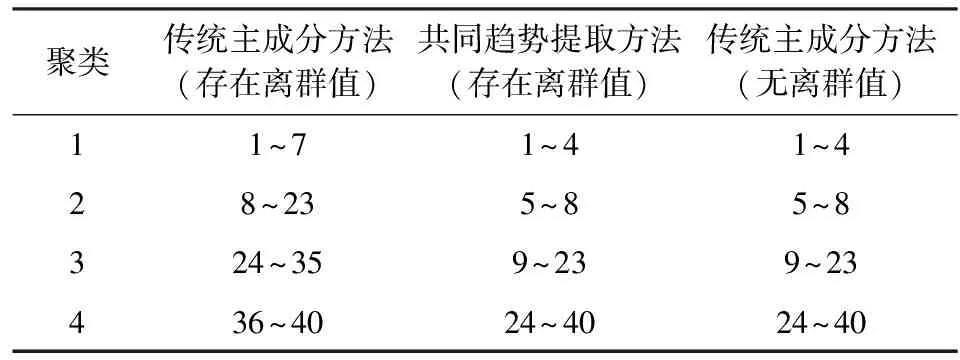
表1 有序聚类结果表

四、实证分析

(一)数据来源

股票价格的变化会受到市场宏观经济的影响，由于其他的不确定因素，不同类型的股票也会出现不同的局部趋势，因此对股票价格整体趋势的挖掘是有必要的。本文选取在上海证券交易所上市的30支股票2016年10月28日至2017年3月23日的日收盘价的99个时点(分别记为时间点1～99)的多维时间序列数据进行有序聚类分析，将最终聚类结果与同期的上证指数趋势变化相比较，证实所提出的方法在多维有序聚类上的表现。

(二)共同趋势提取和聚类结果分析

股票数据是一个30维99个序列点的多维时间序列数据。如图6所示，首先基于共同趋势提取的方法得到了上证30支股票此时间段的趋势变化。

使用共同趋势提取方法提取了30支股票此时间段股价的两种发展趋势。其中，趋势1与趋势2的比例为2∶1，因此趋势1为共同趋势序列，趋势2为含有离群值的异常趋势序列。此外，两种趋势的大部分变化时间点是一致的，但是在时间点30和60附近的变化差异较大，在1～31时段上共同趋势序列明显高于异常趋势序列，在60～99时段上异常趋势序列则明显高于共同趋势序列。可见，在这两处时段和变化时间点附近存在离群值的干扰。

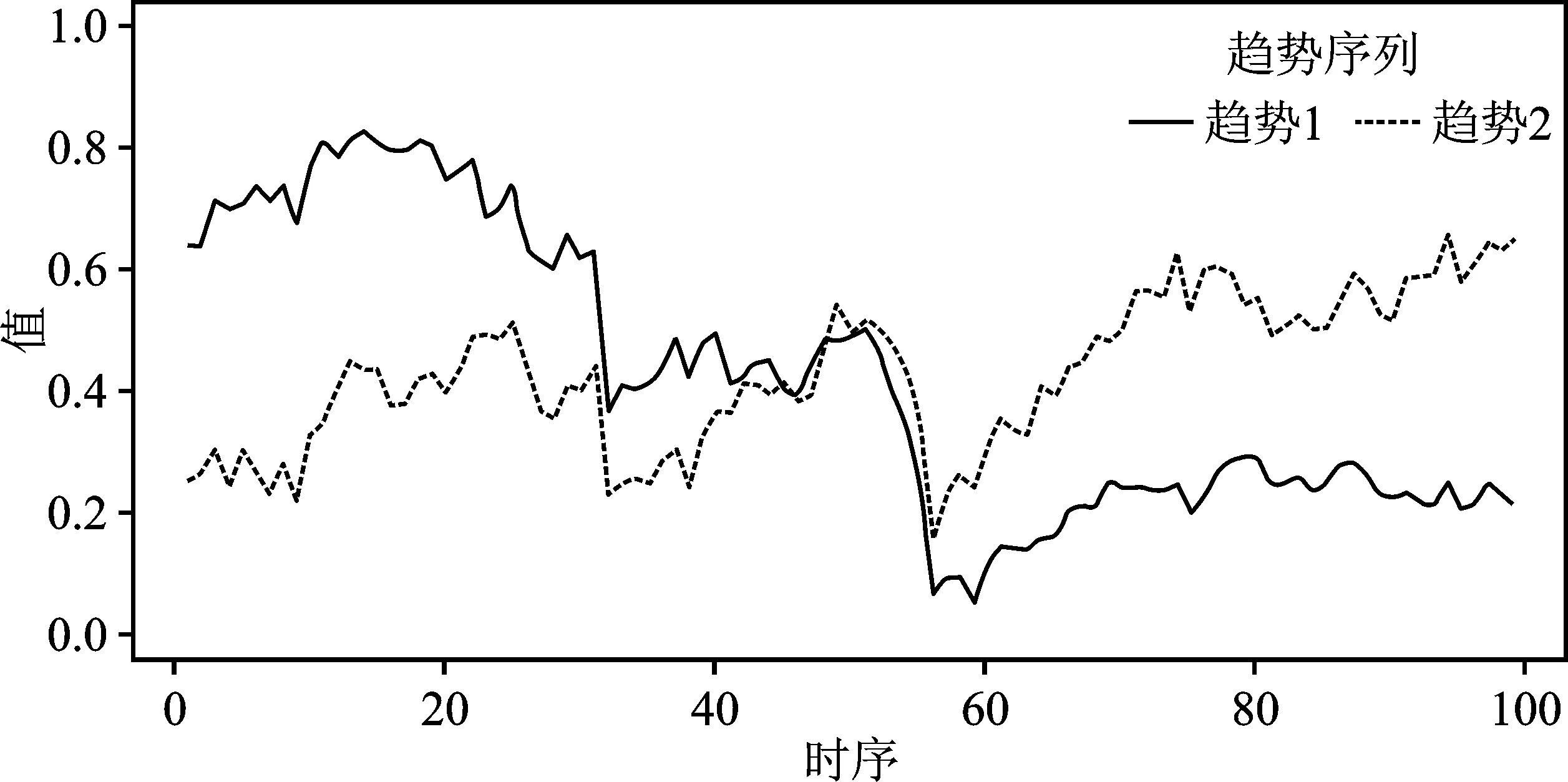
图6 上证30支股票不同趋势的对比图

使用传统主成分方法生成一维有序数据，与本文所提出方法得到的数据进行有序聚类分析，得到图7的聚类折线图，可见在1～31和60～99时段上聚类结果出现了分歧。基于传统主成分方法的有序聚类结果认为，1～31时段内出现了两段聚类区域，但基于共同趋势提取的方法将1～31和66～99时段单独聚为一类，具体分类情况见表2。由此可见，聚类结果的差异主要集中于60～99时段上是否存在两类发展趋势，而对于1～31时段明显应该归为一类，均处于较高的股价水平，因此传统主成分在此出现了误判的情况。

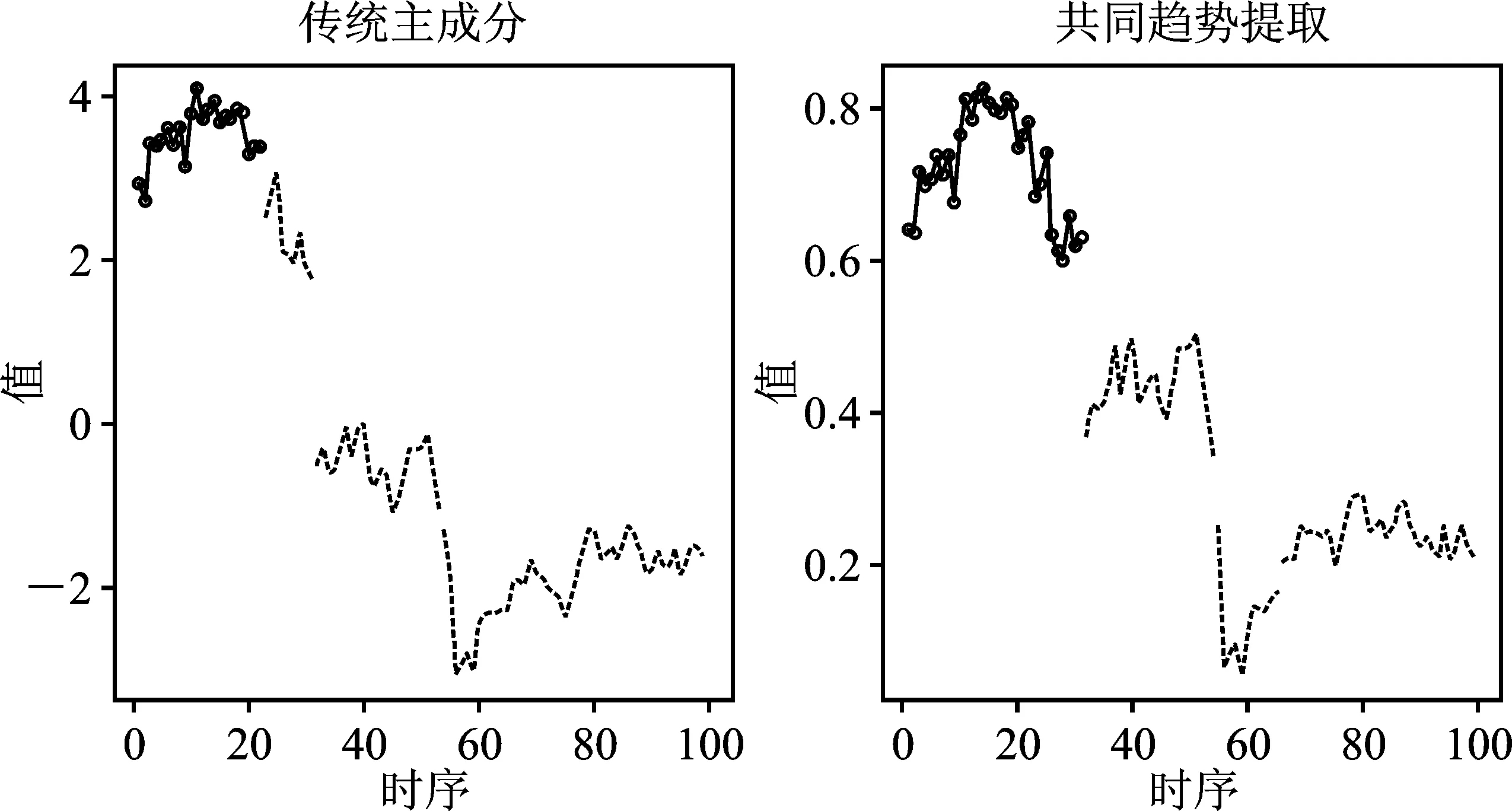
图7 两种方法有序聚类折线图

表2 上证30支股票有序多维聚类结果

(三)聚类结果与实际情况比较

为了与实际情况比较，本文引入同期的上证指数与两种方法进行比较，对比两种方法给出的聚类结果代表这一时间段股票市场的整体趋势的合理性。

根据有序聚类的原理，聚类分割点往往不会在极值处而是在极值的周围，此时的离差平方和较小。由此，通过对上证指数排序发现，最大值中前10的时间点为23，22，25，94，21，97，78，80，77，79；倒数10位的时间点为57，1，46，56，38，4，44，59，2，45。可见，极大值分布在21～25和77～97时点附近，极小值分布在1～4、38～46、56～59附近。

由数据结合图像，1～4的极小值分布区并不明显，因此这一时间段内上证指数存在明显的“两高两低”特征，即：在时间点20、80附近存在高值区域，在时间点40、60附近存在低值区域，说明这一时间段内股票市场存在4个明显的区间。第一阶段为区间高位期，第二阶段为震荡下降期，第三阶段为区间低位期，第四阶段为震荡上升期。

由图8可知，实证结果表明，本文所提出方法的结果完全对应了上证指数的高值和低值区域，而传统主成分方法对时间点20附近的高值区域聚类出现了分化，分为了两个阶段，并且未将时间点60附近的低值区域和时间点80附近的高值区域单独成类。具体而言，在第一次指数到达高值区时，本文所提出的方法准确将这一时间段聚为一类。传统主成分方法则受到离群值影响，将高值区分为两类，与实际情况不符；在第一次指数到达低值区域之后，还有一次上升再下降到达第二次低值区域的过程。本文所提出的方法成功识别了这两个区域，而传统主成分方法却将第二个低值区域和第二个高值区域聚为一类，从而导致了误判。

因此，从实证结果看，基于共同趋势提取的多维有序聚类方法得到的聚类结果与实际的股票市场价格走势趋同，而传统主成分方法出现了两次误判，在聚类精度上远远低于本文所提出的方法。

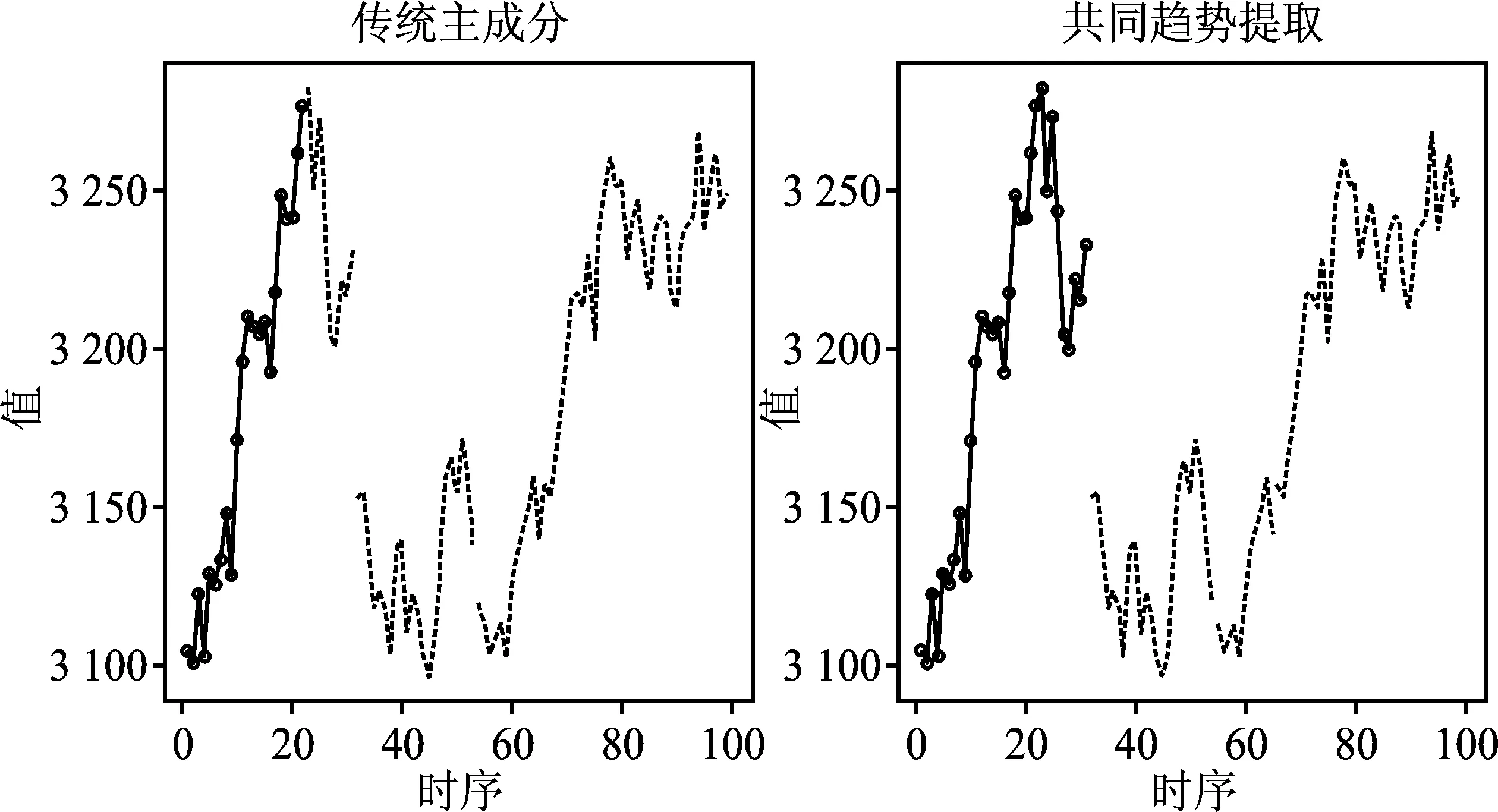
图8 两种方法聚类结果在上证指数上的效果图

五、结 论

针对多维有序聚类研究中很少涉及的数据问题，本文从离群值和序列共同趋势的角度，构建了基于共同趋势提取的多维有序聚类方法。第一阶段通过k-means聚类获得代表了多维有序数据的共同趋势的一维有序序列，其包含了多维有序数据的主要信息；第二阶段通过有序聚类方法获得稳健的聚类结果，其代表了多维有序数据总体的共同趋势。本文所提出的方法不仅剔除了离群值和冗余信息的影响，而且提取了多维有序数据的共同趋势，使分析结果符合多维数据总体的趋势情况。

模拟结果表明，当数据中不存在离群值时，共同趋势提取和传统的主成分有序聚类方法得到的结果差异不大；当数据中存在离群值时，传统主成分有序聚类方法的结果受到离群值的影响大，但是基于共同趋势提取方法的结果与不存在离群值时的结果保持一致。实证结果表明，将基于共同趋势提取的多维有序聚类方法与传统主成分多维有序聚类方法应用到实际数据中时，共同趋势提取方法得到的结果比传统主成分方法得到的结果更具有解释性，体现的信息量更加准确，更加符合实际情况。