中观理念下章起始课的教学实践与思考
2020-12-21刘敬生张秀萍
刘敬生 张秀萍
[摘 要]
在中观理念的指导下,“整式及其加减”章起始课可以划分成“宏观脉络→中观线索→微观落实→课时规划”的教学四部曲。教师在实施过程中,首先应创设情境,使学生初步感受新知识在系统中的地位;通过合作学习的方式,帮助学生理清脉络,探寻中观线索,进行知识建构;然后在微观层面上落实概念的理解。这样才能达到提升课堂教学效率,落实数学核心素养的目的。
[关键词]
初中教学;中观理念;章起始课
中观理念[1]是以数学教学的单元或知识模块为基础,站在系统的高度,用联系的观点对教学内容进行整体设计并落实到课堂教学的一种设计理念。中观介于宏观与微观之间,中观理念强调知识间的逻辑关系和学科思想。教师应站在系统的高度进行教学,使学生学会用联系的方法进行学习,用联系的观点构建知识框架,学会一种思考问题的方式。如今,章起始课教学已成为许多同行关注的话题,如何在教学中有效实施章起始课非常值得探讨。本文以“整式及其加减”为例,谈谈中观理念下章起始课的教学实施与建议,希望能抛砖引玉,引起更多同行加入到此类问题的研究之中。
一、课堂教学流程
(一)创设情境,初步感知
在新知识的学习过程中,教师应让学生感受学习的必要性,章起始课也不例外。在教学中,教师要设计学生熟知的情境问题,引导学生回顾旧知识,引出新知识,使学生感受到新知识“有用”,激发学生学习的兴趣。
PPT展示学生熟悉的儿歌。
1只青蛙1张嘴,_____只眼睛_____条腿;
2只青蛙2张嘴,_____只眼睛_____条腿;
……
_____只青蛙_____张嘴,_____只眼睛_____条腿。
问题1:刚才的儿歌,你是用什么方法表示青蛙的只数、眼睛和腿的个数呢?
追问:你还能举出字母表示数的例子么?
通过对话交流,引出“用字母表示数”,在举例中提炼出小学学习的各类式子。
教师板书:s=vt,2a+ab,s/t,a,2a等。
设计意图:章起始课知识的呈现要基于学生已有的认知,将学生已有经验作为知识的生长点。青蛙儿歌情境的引入,将知识从数自然地过渡到了“式”,符合学生的认知,激发了学生的学习兴趣,同时让学生初步感受到了代数式学习的必要性和合理性。举例过程回顾了小学学习过的各类式子,使学生体会到了用字母表示数应用的广泛性,为下一环节做好了铺垫。
(二)合作学习,理清脉络
任何单元知识都是知识系统的一部分,学习新单元知识时,教师要让学生从宏观上理解知识的来龙去脉。在教学中,教师要基于学情开展合适的探究活动,使学生在活动中体验新知识的演变过程,从宏观上理解单元知识在初中数学知识体系中的地位和作用,确立学习的计划和方向。
问题2:你能对刚才举例中的式子进行分类吗?
学生独立分类,小组讨论后班内分享。根据式子中是否含有关系符号(如等号、不等号等),“式”可以分为关系式和代数式;通过类比有理数的分类,又可以将例子中的代数式分为整式和分式。教师要明确指出整式和分式是初中数学的重要知识,点出本单元主要学习整式,引出课题。
设计意图:学生通过对不同类型的式子进行分类,构建“式”的知识体系,初步感知“式”的宏观脉络,理解整式在“式”中的地位。教师通过对话活动,用具体实例让学生感知“式”的多樣性,并将所学过的“式”进行分类,区分关系式和代数式,然后类比有理数,将代数式初步分成整式和分式。由此,学生对“式”的宏观脉络有了初步的认知。“式”的宏观脉络虽不完善,却使学生初步明确了整式在“式”的体系中所处的地位。
(三)探寻线索,知识建构
章起始课中的中观线索是理清知识间联系的路径,为章起始课的教和学提供方向。中观线索通常以思维导图或结构图的形式展现单元知识间的逻辑关系,是对单元知识有序整合的思维展示。中观线索的构建,通常运用课题联想和类比联想的策略,既要构建本单元知识结构,又要理清基本概念与运算间的联系。
1.初步构建知识框架
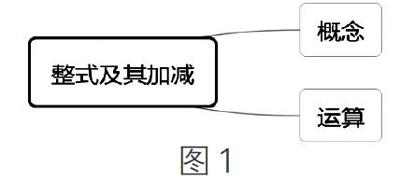
PPT展示本章标题“整式及其加减”。教师通过课题联想策略,确定本单元教学的关键词为整式和加减,明确加减是一种数学运算,初步构建知识结构(见图1)。
2.完善知识框架
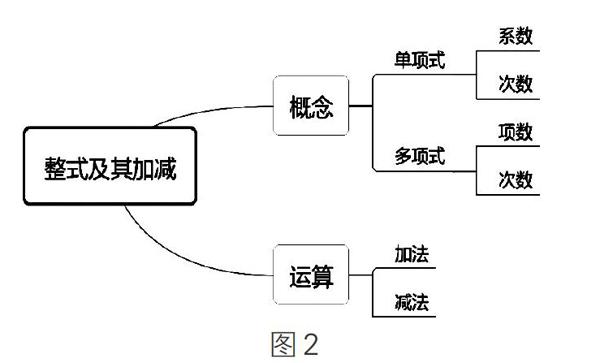
教师启发学生对图1展开联想,学生提出如下问题:①什么是整式?②整式还包括什么样的式子?③整式如何进行加减运算?学生带着问题,在教师的引导下阅读教科书,然后自主完善知识结构图,经全班讨论后,形成知识结构(见图2)。
3.从概念角度认识数和式
教师相继提出三个有关数的问题:①能否由数字1得到所有的自然数?②能否由自然数得到所有的整数?③能否由整数得到所有的分数?教师引导学生得出结论:数字1通过加减乘除运算能演变出所有的有理数。类比有理数的演变过程,通过举例,由数字和字母演变出不同的代数式,师生总结出代数式的定义,并对其中的整式进行辨析。
4.从运算认识数和式
问题3:小明一家6人去肯德基点餐,他们都要汉堡、可乐、薯条。你觉得小明会怎样和服务员说呢?(学生回答如何点餐,教师适当点评。)
问题4:157+23怎样用列竖式计算?(教师引导学生得出结论“同类”才能加减)
问题5:如下整式中哪些能进行加减运算?
x,3x,x2,xy,-2x2,12xy,-2x2y,6x2y
学生初步分类后,教师引导学生理解整式中的“同类”是指同类项。
问题6:单项式是如何相加的呢?(教师引导学生理解同类项相加就是系数相加)
问题7:多项式[(3x+4xy),(2x+3xy)]能加减运算么?怎么运算呢?
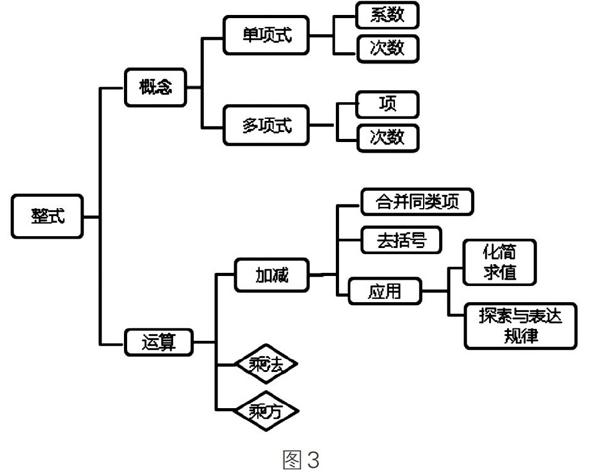
学生交流,形成共识:整式的加减运算就是合并同类项。至此,构建出本节课的中观线索(见图3)。
设计意图:通过课题解读策略,教师初步概括出本单元的知识结构,在学生自主阅读教科书的基础上,完善知识结构图(图2)。类比整数,从概念和运算两方面加深对整式概念和加减运算的认识,构建本节课的中观线索(图3)。体会整式概念各要素之间的联系和整式加减运算的本质,感悟分类、类比等思想方法,使学生站在更高的角度审视本章知识。
(四)微观落实,理解概念
章起始课的首要任务是构建中观线索,感悟知识间的联系。在构建中观线索的过程中,一些微观知识的落实十分必要。微观知识的落实要根据本单元知识的内在逻辑关系,以中观视角选取那些相对独立的、容易理解的知识进行。
1.理解概念
问题8:你能举例说明什么是单项式和多项式吗?
学生回答单项式和多项式的定义,教师引导学生举例辨析单项式中的系数和次数、多项式中的项和次数。
2.课堂检测
(因篇幅问题,此处略)
设计意图:在微观落实环节中,通过具体例子的讨论和变式练习,进一步加深学生对单项式和多项式的理解,使学生掌握整式的概念,为加深理解本单元知识间的联系奠定了基础。
(五)课时规划,明确进度
問题9:通过今天的学习,我们对这一章的知识有了全新的认识,那么我们接下来将分几课时学习完本章呢?
PPT展示课时安排表(见图4),教师讲解后续课时的规划。
设计意图:通过课时规划,教师将本章剩余的知识以思维导图的形式呈现给学生。教师进行必要的讲解,使学生明确后续学习的重点及课时数,做到心中有“数”。这样做提高了学生的学习积极性,便于学生课后开展自主性探究学习。
二、教学后的思考
对于章起始课的教学研究,多数同行关注到了它的教学意义和教学原则,对于每一单元内容的教学模式却研究较少。章起始课的研究是一个逐步深入、螺旋上升的过程,如何在中观理念的指导下探索章起始课教学实施的有效模式迫在眉睫。对于此类课的教学,笔者探索了“宏观脉络→中观线索→微观落实→课时规划”的四部曲,在教学实践中取得了非常理想的效果,并总结出以下四点实施建议。
(一)基于学情创设适宜情境,引导学生感受知识在系统中的地位
数学知识具有很强的系统性,知识之间是相互联系的。在学习一个新章节时,从宏观上理解知识产生的过程以及所处的地位和作用,可以让学生对新知识的理解更加深入。教师要深刻理解知识发生、发展的过程,基于学生的知识和生活经验创设适宜情境,找准单元知识的生长点,使学生体会本单元知识在初中数学知识体系中的地位和作用,激发学生学习的兴趣。如在上文的教学中,教师用学生熟悉的儿歌创设情境,完成从“数”到“式”的过渡,进而通过对“式”的分类,明晰整式在“式”这一系统中的地位和作用,并明确了后续学习的方向和目标。这一环节可以促进学生后续学习的进程,使学生习得的知识在大脑中进行有序储存,保证了知识的快速提取,提高了学习效率。
(二)用类比联想的策略设计问题串,构建知识框架
特级教师卜以楼先生曾说:“类比联想是发现问题的一种思维方式。”[2]教师通过类比联想设计相关问题串,可以帮助学生打通知识之间的联系通道,使知识能够在学生头脑中以框架结构储存,加深学生对知识内涵和外延的理解。类比联想的策略就是通过已有的知识经验来带动新知识的感悟和体验,使学生充满求知欲,降低学生对未知知识的畏惧感,提高他们学好数学的自信心。以上文的教学为例,教师通过分解课题名称中的关键词“整式”和“加减”,引导学生产生联想,得出本单元的知识学习主要从整式的概念和运算两个角度进行,然后通过问题串的形式建立“数”和“式”的联系。活动一通过引导学生类比有理数理解整式的相关概念和分类,活动二引导学生类比整数、小数和分数的运算本质——“同类可加减”,得出整式加减运算的本质——合并同类项[3]。在整个环节中,教师均以问题串的形式引导学生进行自我构建,最终构建了本章的知识框架。
(三)以中观的视角进行筛选,夯实纽带性知识
章起始课的首要任务是帮助学生学会学习,找准同类知识的学习路径,解决“怎么学”的问题。在打通知识联系通道的过程中,一些基本的、纽带性的知识必须深入理解,当堂落实。所谓纽带性知识是指那些相对独立、简单易懂且能在知识的联系中起关键作用的概念、法则等。在上文中,单项式、单项式的次数和系数、多项式、多项式的项和次数等知识,对于联系整式概念和加减运算起着关键作用。倘若学生对单项式的次数和系数掌握不到位,对合并同类项法则的本质(“同类”相加减)就无法理解,也很难对整数的加减法则进行有效迁移,那么“怎么学”的问题就难以实现。
(四)以全局观点进行知识梳理,明确课时规划
在课堂教学中,知识的小结和梳理都必不可少,章起始课也不例外。教师在进行知识梳理时,要以全局观点引导学生审视本章的知识框架,了解知识间是如何生长的,并以此来积累同类知识的学习经验。如上文,教师要让这节课的学习活动成为后续学习分式、二次根式等“式”的种子课。此外,规划好本单元后续学习的主要内容和课时也十分必要,如本节课已经落实了整式的概念,后续的课时就是深入研究整式的加减运算。教师还应通过思维导图的形式让学生明确要学习的内容和课时,指明学习的方向,提升学习的主动性和积极性,培养自主学习能力。
[参 考 文 献]
[1]李传英,韦凤莲.做知“道”的教育(上):“中观课堂”的思考与实践[J].山东教育,2017(9):35.
[2]卜以楼.生长数学:卜以楼初中数学教学主张[M].西安:陕西师范大学出版总社,2018:222.
[3]李传英,韦凤莲.做知“道”的教育(中):国家课程校本化之中观课程[J].山东教育,2017(12):42.
(责任编辑:赵晓梅)
作者简介:刘敬生(1982-),男,山东博兴人,中学一级教师,硕士,研究方向:初中数学教学;张秀萍(1983-),女,山东莱芜人,中学一级教师,硕士,研究方向:初中数学教学。
