高温无机晶体材料比热容的双参数预测方法

魏小林，李 腾，李 博，孙 岑

(1.中国科学院 力学研究所 高温气体动力学国家重点实验室，北京 100190；2.中国科学院大学 工程科学学院，北京 100049)

0 引 言

高温固体是工业流程中的常见物料，如钢铁行业与有色金属行业中的高温冶金渣(1 500～1 900 K)、烧结热矿料(1 000～1 100 K)，以及干熄焦过程中的红焦炭(1 200～1 300 K)；建材行业的高温水泥熟料(1 700 K)、烧成陶瓷(1 400～1 600 K)；矿热炉中2 200 K以上的电石等[1-4]；还有自然界中正在凝结的火山熔岩(约1 500 K)等。确定固体的比热容一般采用热量计等方法[5]，但由于高温下测量困难，工作量大，因此固体比热容经常只存在有限温度范围内的测量数据[6-8]，许多含有复杂晶格晶体的高温固体比热容数据经常缺失或不准确。因此研究高温固体比热容的理论预测方法具有重要意义。

固体中相邻原子(或离子间)的距离很小(几个埃)，一般以金属键、离子键或共价键结合，原子之间的相互作用很强，如金属键、离子键或共价键键能为200～400 kJ/mol[9]。固体中的内能主要产生于每个原子在其平衡位置附近做的微振动，因此在考虑固体比热容的影响因素时，不考虑原子平动和转动的影响，只考虑微振动，这样统计热力学就从固体的微观结构出发给出了固体比热容的理论计算方法[10-11]。

若固体中有N个原子，每个原子有3个自由度(即3个振动的方向)，即固体共有3N个振动自由度，可以将固体的热运动描述为3N个相互作用的简谐振动，称为简正振动[11-12]。按照能量均分定律，每个简正振动的原子能量包括动能与势能之和，各为1/2kT(k为玻尔兹曼常数，T为温度)，一个原子的平均能量则为3kT，因此，不考虑温度对于固体比热容的影响时，经典的杜隆-珀蒂定律给出固体的热容量为3Nk。统计热力学从玻色量子统计理论出发，将简正振动的能量量子看成一种准粒子，称为声子，将固体中的3N个有相互作用的原子系统简化为声子理想气体，从而用玻色分布来分析固体的热运动[11-12]。

为了计算固体热运动的能量，需知道3N个简正振动的频率ωi。简正振动的频谱特性可以通过试验测得[13]，也可以采用某种假设的频谱模型。对于一维单原子晶体，2种常见的频谱模型是爱因斯坦模型和德拜模型[12-13]。爱因斯坦假设每个简正振动的频率相同，从而得出以指数形式表达的固体定容比热容。德拜提出一种声子谱模型，将固体作为连续弹性介质，所有的简正振动形成3N支在固体中传播的低频弹性波；假设3N个简正振动为一系列频率为ωi(i= 1,2,…,3N)的低频振动，每一个振动都对应晶体点阵中传播的振动波，其能量是量子化的，以hωi为单元，从而得出以积分形式表达的固体定容比热容。

Inaba通过分析以上2种模型，基于试验结果建立了一种半经验的单参数固体比热容计算模型。比热容方程采用指数形式，而不是德拜模型的积分形式；特征温度为重新定义的一维德拜特征温度，对于玻璃状氧化物的比热容进行了比较成功的预测[14-15]。徐辉等[16]考虑了固体的晶格振动热容、电子热容、晶体点缺陷热容等因素，将固体比热容的拟合计算式表达为含有2个特征温度的指数项、1个温度一次方项的非线性多项式；在实际测试固体比热容时，只需得到有限几个温度点的比热容数据，即可通过非线性拟合的方法确定公式中的参数，从而得到固体材料各个温度的比热容，计算准确度可以满足一般工程需要。但这些方法基本通过对试验数据的重新处理和拟合得到。

在应用过程中，爱因斯坦模型和德拜模型仅适用于简单的单原子晶体或某些双原子晶体，且德拜温度或爱因斯坦温度经常难以准确获得，因此采用这些模型方法准确预测含有多个原子与复杂晶格的固体比热容比较困难。本文采用统计热力学方法，基于玻恩的固体晶格同时存在声频与光频振动的理论[12,15-16]，提出一种高温固体比热容的双参数预测方法，仅通过固体比热容的有限试验数据或简单物质的热物性，即可较准确地预测不同温度下固体的理论比热容，以期为确定流程工业的固体热物性数据，提供一种简单可靠的新方法。

1 模型与方法

1.1 简单晶体比热容模型

爱因斯坦模型和德拜模型主要是针对一维单原子晶体提出和验证[10-12]。爱因斯坦模型假设晶格只有一种频率的振动，均为爱因斯坦特征频率，表示为ωE，从而推导出固体中单原子的定容比热容cV[12-13]。

(1)

ΘE=hωE/k，

(2)

式中，ωE为爱因斯坦模型中固体内声子的圆频率；h为普朗克常数。

对于固体的比热容，爱因斯坦模型假设晶格只有一种频率的振动，而实际晶格的振动存在频率密度函数[13]，因此德拜假设固体为均匀的各向同性连续介质，弹性波可以分为1个纵波(膨胀压缩波)和2个横波(剪切波)，共代表3N个简正振动模式。因此将固体中的弹性波看成声子理想气体，从而推导出固体中单原子的定容比热容[12-13]。

(3)

ΘD=hωD/k，

(4)

其中，ωD为德拜模型中固体内声子的圆频率。德拜模型中单位体积简正振动的数密度定义为声子的态密度，可以计算出声子态密度[13]为

(5)

其中，c为固体中弹性波的平均体波速度。可见德拜模型的声学振型遵守ω2的变化特性(平方关系)，而爱因斯坦模型的光学振型态密度遵守ω的变化特性(线性关系)。德拜模型适用于低频的声学振型，适宜预测低温固体比热容；用于较高频的振型会出现较大偏差，导致预测的晶格比热容偏离试验值[17]。光学振型的态密度g(ω)通常有一个最大的峰值，在常温或高温时，即kT≥hωE时，爱因斯坦模型近似给出了态密度中最重要的部分，因此在预测高温固体比热容时，该模型非常关键。

1.2 含复杂晶格的固体比热容模型

对于一维双原子晶格晶体，原子质量分别为m和M时，由于原子质量不同，会出现2种高低不同频率的振型，因此多原子晶体的实际晶格振动存在较复杂的频率密度函数[13]。对于多个原子的复杂晶格晶体，玻恩提出将晶格振型分为2类：声学支和光学支[13,17-18]。对于低频的声学支，可采用德拜模型，将一个晶格晶胞(基元)看作一个分子，声学支共有3组振型，共含3N0个频率(N0为固体晶格原胞数)；对于高频光学支，可采用爱因斯坦模型，若假设每个晶格原胞的原子数为p，则有3(p-1)组振型，共包含3N0(p-1)个光学频率。

包含多原子的复杂晶格晶体定容比热容定义为声学支与光学支的贡献之和[13]，即

(6)

对于复杂晶格晶体固体的比热容计算，假设多原子组成的单个晶格原胞具有唯一的德拜特征温度ΘD和爱因斯坦温度(ΘE)，固体比热容由式(6)确定。本文的新思路是通过晶体学的基本参数和简单物质的热物性，预测得到ΘD、ΘE，从而推算出不同温度下固体的理论比热容，通过与试验数据的相互验证，获得高温固体比热容的双参数表达式。

式(6)中，由于N0k=R(R为气体通用常数)[9]，因此比热容的双参数计算式为

(7)

在本文固体比热容计算中，爱因斯坦温度是试凑数据，目的是保证式(7)可以正确预测比热容，其实际数据与固体比热容爱因斯坦模型中的数据不同，但物理意义不变，其值仍大于德拜温度。

1.3 高温固体比热容双参数的确定方法

(8)

式中，D(x)为德拜函数，即

(9)

德拜比热容函数计算式比较复杂，本文为方便计算，采用文献给出的该函数列表数值[17-18]，得到德拜比热容函数的拟合式为

fD(x)=0.999 95+0.000 762x-0.052 5x2+0.002 72x3+

0.000 765x4，

(10)

式中，x取值小于2时(即高温区)，计算值的误差小于0.015%。

德拜温度与固体的弹性波速度有关，可以采用式(11)确定[19-20]。

(11)

式中，V为每千摩尔固体的体积，m3；c为固体中弹性波的体波速度。

(12)

其中，cl、ct分别为纵波波速和横波波速。由于每kmol(N0=6.022 141 79×1026kmol-1)固体的质量可表达为

M=ρV,

(13)

其中，M、ρ分别为每千摩尔固体的分子量(kg/kmol)和密度(kg/m3)，因此有1/V=ρ/M，代入式(11)可以得德拜温度[19]。

(14)

其中固体中弹性波的体波速度c由式(12)得到。

(15)

计算时，关键参数体波速度c通过固体的弹性模量确定。假设固体为各向同性的弹性物质，固体中传播的纵波波速与横波波速计算公式[21-22]为

(16)

(17)

式中，λ、μ分别为固体的第一和第二拉梅弹性常数。

固体常用的弹性模量为体积弹性模量和剪切弹性模量，体积弹性模量K是固体压缩系数的倒数，剪切弹性模量G=μ。固体的弹性模量是固体发生弹性形变时的固有性质，与固体的原子组成与晶格结构密切相关。体积弹性模量K满足[23]

(18)

应用μ=G，并将式(18)的λ带入式(16)和(17)，即可得到固体中传播的纵波波速与横波波速为

(19)

(20)

固体的体积弹性模量(K)和剪切弹性模量(G)可以通过试验得到，也可以通过量子化学计算获得基本参数，然后采用Voigt-Reuss-Hill(VRH)方程通过固体弹性刚度常数和弹性顺度系数计算得到[24]。本文计算中采用美国加州大学伯克利分校晶体学网站提供的数据[25]，包括晶体的密度以及在VRH近似下的体积弹性模量(K)和剪切弹性模量(G)，从而通过式(19)和(20)得到固体中传播的纵波波速与横波波速，采用式(15)获得固体中弹性波的体波速度c，并通过式(14)获得德拜温度ΘD。

(21)

该函数可直接计算，文献[18]给出了其数值，为计算方便，本文给出了爱因斯坦函数拟合式为

fE(x)=0.999 8+0.003 12x-0.092 2x2+0.008 84x3

+0.001 01x4，

(22)

x取值小于2时(即高温区)，计算误差小于0.02%。

确定式(7)中的ΘE比较困难。当晶体中原子数较多时(p值较大)，由于爱因斯坦项成为比热容的主要贡献项，因此准确获取ΘE很重要。本文采用以下2个思路之一来解决：

2)构造一个该固体物质的生成反应

(23)

(24)

利用基尔霍夫方程[9,26]，可以得到不同温度下标准反应热效应随温度的变化关系为

(25)

式中，Δcp为生成物的摩尔定压比热容之和与反应物的摩尔定压比热容的差值，即反应摩尔比热容差。

Δcp=∑iaicp,i-bcp,b，

(26)

(27)

Δcp=∑iaicp,i-bcp,b=0，

(28)

(29)

1.4 比热容公式的修正

将晶体的德拜温度与爱因斯坦温度等数据代入式(7)，还可进行自由电子比热容以及定压比热容和定容比热容的修正。当计算含自由电子(如金属)等固体比热容时，自由电子比热容[13]为

(30)

其中，TF为金属的费米温度。式(30)得到的自由电子作为附加比热容，可修正比热容公式(7)。

由于随温度变化时，固体会发生体积膨胀等变化，因此固体的定压比热容与定容比热容随温度有微小变化[17-18]。确定定容比热容后，可采用式(31)获得修正后的定压比热容[18-19]。

cp-cV=ATcp，

(31)

(32)

由式(31)得出

(33)

由式(7)得到固体的定容比热容后，通过式(33)得到定压比热容。对于具有复杂晶格的晶体，文献[20]给出的A0数值有数量级变化，如A0=1～10×10-3K·mol/J(对于晶格的单原子)，因此实际计算时可对A0取值进行适当调整，从而使得定压比热容的理论结果更接近实际值。

针对固体的定压比热容与定容比热容的修正，计算时通过晶体的熔点考虑固体的热膨胀等因素，但由于不同实际固体在熔点附近的膨胀特性有一定差异，同时部分晶体的熔点无法查询，只能采用估计的熔点，因此比热容修正式(33)不确定性很小。

2 结果与分析

计算比热容时不同晶体的主要参数见表1，晶体的体积弹性模量K和剪切弹性模量G来自晶体学网站[25]。德拜温度ΘD利用式(14)计算，爱因斯坦温度ΘE利用双参数比热容计算式(7)反算得到。德拜温度仅依赖于晶体的基本参数，具有明确的物理意义，代表比热容项中的声学支；爱因斯坦温度代表比热容项中光学支的影响，数值大于德拜温度，但为了保证比热容的预测精度，具体数值有一定的拟合成分。从固体的晶体结构看，一种晶体往往存在多个同分异性体[25]，即虽然分子式相同，但原子排列不同，从而晶型也不同，因此这些晶体构型的基本参数(如密度、弹性模量和熔点等)会有变化。在德拜计算中，用不同晶型的基本参数进行对比试算，发现得到的德拜温度差别不大。

表1 计算比热容时晶体的主要参数

2.1 简单晶体的比热容

首先用双参数比热容预测方法计算了简单的金属铜晶体(单原子Cu)的比热容。由表1可知，铜的德拜温度为350.5 K，而文献给出的数值为345 K[10]，两者误差仅1.59%，这是因为单原子晶体的结果与德拜理论最为接近。

不同温度下的铜比热容预测值如图1所示，预测的比热容值(空心方块)与文献[26](实心方块)相比，最大误差为2.865%。该比热容的计算只考虑了金属原子振动的比热容，没有考虑金属中自由电子的比热容。温度较高，与金属中的自由电子温度特征温度(对于Cu，ΘE=82 000 K)可以相比时，电子比热容按照式(30)进行修正。由图1可知，经过电子比热容的修正，铜比热容的预测值(空心圆圈)最大误差下降至1.312%，精确度很高。

图1 铜的比热容

MgO、SiO2和Al2O3的比热容如图2所示。由图2(a)可知，MgO比热容的预测值与文献[26]非常接近，最大误差为1.095%；根据HSC软件和文献[6]给出的MgO比热容，可以看出不同文献的比热容具有明显差别，特别是文献[6]的比热容在高温下明显比其他比热容值大。图2(b)为了减少预测误差，将温度分为298～400 K和400～2 000 K两个区段，SiO2比热容的预测值与文献[26]在1 000 K存在最大误差(-4.905%)，而HSC软件给出的比热容值与这些值偏差均较大。图2(c)温度也被分为298～800 K和900～2 327 K两个区段，Al2O3比热容与文献[26]比较接近，最大误差为-2.828%；而文献[6]给出的Al2O3比热容，与预测值非常接近。因此本文比热容的预测值具有很好的精度，其误差已经小于不同文献之间的比热容误差。

图2 MgO、SiO2和Al2O3的比热容

2.2 复杂晶格晶体的比热容

具有多原子的复杂晶格固体MgAl2O4、Mg2SiO4和Al2SiO5的比热容如图3所示。由图3(a)可知，MgAl2O4的比热容预测值与文献[26]的误差随温度升高增大，最大误差为5.754%；由HSC软件给出的比热容值为最大，与预测值最大相差12%以上。图3(b)中Mg2SiO4比热容的预测值与文献[26]在800 K存在最大误差(-3.065%)，其他比热容值与该值比较接近。图3(c)中Al2SiO5比热容与文献值均很接近，而预测值比文献[26]大，900 K时存在最大误差(-4.923%)。因此对于MgAl2O4的比热容，预测误差随温度升高而增大；对于Mg2SiO4、Al2SiO5的比热容，在比热容曲线的拐点附近，比热容存在最大误差。

图3 MgAl2O4(MgO·Al2O3)、Mg2SiO4(2MgO·SiO2)和Al2SiO5(Al2O3·SiO2)的比热容

具有29个原子的复杂晶格固体Mg2Al4Si5O18(2MgO·2Al2O3·5SiO2)的比热容如图4所示，可知其比热容预测值比文献[26]大，随温度升高预测误差不断变大，最大误差为-7.081%。为了减小误差，调整式(32)中A0=3.11×10-3K·mol/J，这时比热容预测值的最大误差减少为3.474%。可见微调A0可以明显提高比热容预测的精度。

图4 2MgO·2Al2O3·5SiO2的比热容

晶体Mg3Al2(SiO4)3(3MgO·Al2O3·3SiO2)的比热容很难查到，因此采用本文提出的方法，对其进行预测计算。首先给出3MgO·Al2O3·3SiO2的生成反应式[26]为

2(2MgO·2Al2O3·5SiO2)+(MgO·Al2O3)+

(34)

已知3种生成物的比热容(图3(a)、(b)和图4)，采用式(29)获得298 K时3MgO·Al2O3·3SiO2的比热容(311.752 J/(mol·K)；然后采用类似方法，预测出该固体在不同温度下的比热容(图5)。由于该固体的比热容完全来自于预测计算，其精确性有待验证。

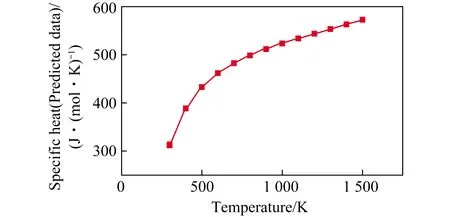
图5 3MgO·Al2O3·3SiO2的比热容

3 结 论

1)本文基于统计热力学方法，提出一种高温固体比热容的双参数预测方法，采用该方法对典型单原子、双原子与多原子晶体的比热容进行预测计算，并通过试验数据进行对比验证。

2)将固体晶格振型分为声学支与光学支，假设多原子组成的复杂晶格比热容主要影响因素为2个参数：德拜特征温度ΘD和爱因斯坦温度ΘE；通过晶体学的基本参数获得德拜特征温度ΘD，再通过固体比热容的有限试验数据或简单物质的热物性，反算出复杂晶格固体的爱因斯坦温度ΘE，从而预测得到不同温度下固体的理论比热容。

3)从预测得到的固体比热容与实际值对比发现，比热容预测误差主要有2种形式：一是在温度拐点附近，误差较大，即在温度区间内体现为两头精度高、中间误差大，可以采用温度分区的办法来减少误差(如Al2O3和SiO2的比热容)；二是随温度升高，比热容误差加大(如MgAl2O4和Mg2Al4Si5O18的比热容)，可以通过调整比热容修正式中的A0来微调定压比热容的预测值。温度分区与调整参数A0两种方法也可以结合起来微调比热容。

4)该方法在宽范围变化的温度区间内可以保证比热容的预测误差小于5%，说明高温固体比热容双参数表达式有望为流程工业的固体热物性数据，提供一种简单可靠的确定方法。实际晶体的比热容由晶格振动比热容、电子比热容、晶格缺陷比热容等组成，本文在计算中基本未考虑电子比热容、晶格缺陷比热容等因素的影响，这是下一步研究方向。