包含Bernoulli 多项式的正整数的m 次方部分之和

朱萍萍，洪海燕

1993年，罗马尼亚数学家F.SMARANDACHE在其论著中提出了一些新的函数，并且列举了100 多个未曾解决的问题及猜想，众多学者都对其中的很多问题进行了深入细致的研究，并获得了一定的成果［1-3］.

对于任意大于1 的正整数m，n，设fm(n)是不小于n的最小m次方部分，例如f3(1)= 1，f3(2)= 8，f3(3)= 8，f3(4)= 8，f3(5)= 8，f3(6)=8，f3(7)= 8，f3(8)= 8.

设Sm(n)是不小于n的所有正整数的m次方 部 分 之 和，即文献［4］利用初等方法研究了fm(n)的均值性质，并给出了fm(n)的渐近性公式；文献［5］利用解析法给出了fm(n)及除数函数的渐近性公式；文献［6］利用初等法和解析法研究了正整数的四次方数列求和问题，给出了S4(n)的计算公式，即但 是并没有给出Sm(n)的计算公式.文献［7］直接利用f3(n)的性质，给出了S3(n)的计算公式，即而当k= 2，n= 8 时，S3(8)= 11.6 不是整数，文献［7］所给的公式是错误的.

鉴于目前仍未有学者研究Sm(n)的一般性公式及渐近性，本文根据Bernoulli 多项式与连续正整数的齐次和的关系式，推导出了Sm(n)的一般性计算公式及其渐近性，得到相应结论.

1 主要结果

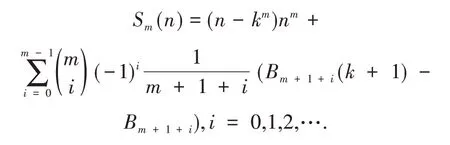
由定义可知Sm(n)= (1m- 0m)1m+ (2m-1m)2m+ 3m(3m- 2m) + …(n-km)nm，即

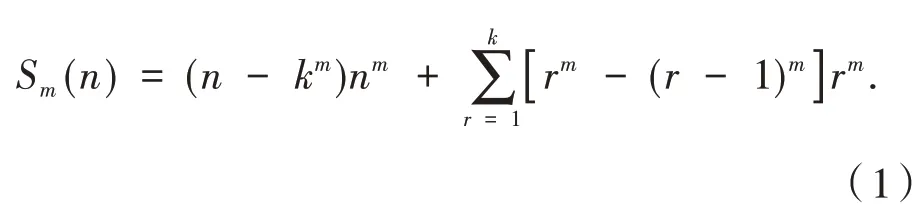
根据二项式定理［8］可知

对于正整数c和t，设

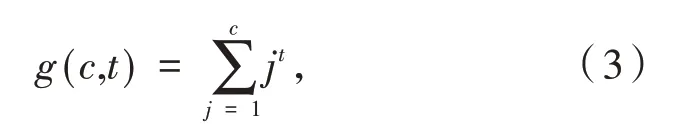
所以有

结合（3）式，可得

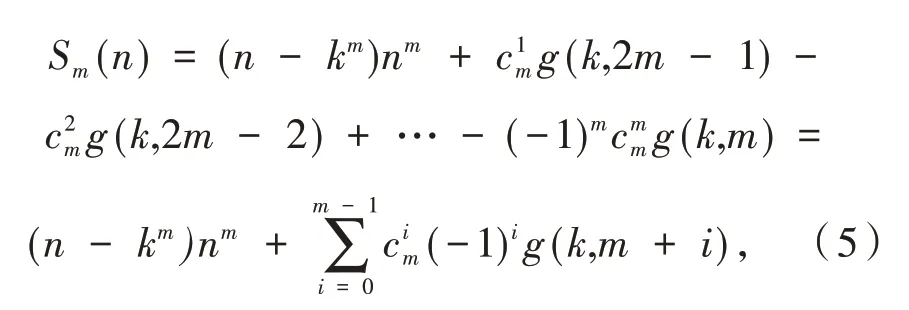
由其 中Bt+1与Bt+1(c+ 1) 分 别 是 第t+ 1个Bernoulli 数和Bernoulli 多项式，因而

由式（5）及式（6）式可得定理1.

证 明 由当n→∞时，有k→∞，且(k- 1)m＜n≤km，显然有

又由

可得

而当i=m- 1 时，

由定理1 及式（7）、式（8）、式（9）、式（10）可得推论1.

2 结语

对于连续正整数的m次方部分和的研究，笔者引入了正整数的齐次和与Bemoulli 多项式之间的关系式，再借助二项式定理展开式推导出Sm(n)的一般性计算公式，该方法可用于推导出Tm(n)的一般性计算公式及其渐进性（设Tm(n)是不大于n的所有正整数的m次方部分和），有兴趣的读者可以尝试.