多参数复合核的Hilbert 型不等式及应用

有名辉，董 飞，何振华

若f(x),g(y) ≥0，且满足f,g∈L2(R+)，则Hilbert 不等式通常可表述为［1］：

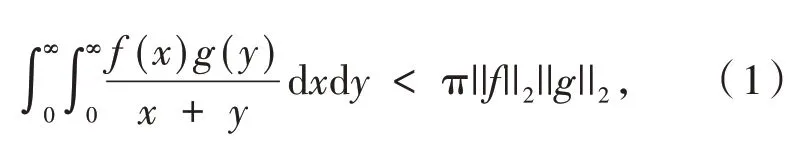
其中：π 是满足式（1）的最佳常数因子.此外，文献［1］中还给出了与式（1）类似的含有对数函数核的不等式

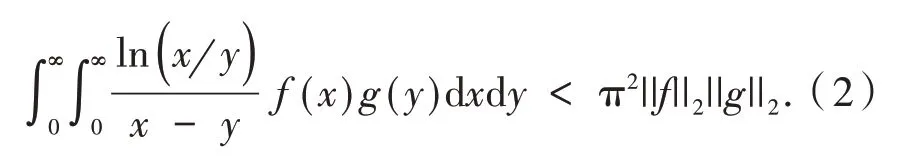
其中：π2是满足式（2）的最佳常数因子. 式（2）通常被称为Hilbert 型不等式，通过对核函数进行推广、类比等不断的演化，数学工作者们已经建立了形形色色的Hilbert 型不等式［2-10］.这些新不等式的建立借助了许多经典分析的技巧，同时又在很大程度上促进了现代分析的发展.与式（2）类似的，还有杨必成［11］建立基本的Hilbert 型不等式

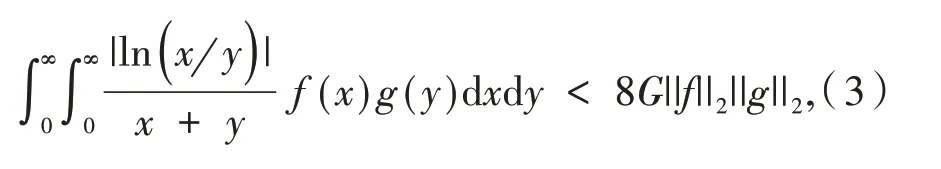
其中：G= 0.9159…为Catalan 常数.其它一些与对数函数关联的Hilbert 型不等式可参见文献［12］～［14］.另外，通过构造对数函数和指数函数复合而成的核函数，刘琼［15］构建了Hilbert 型不等式

其中：μ(x)=x-3，ν(y)=y-3.受文献［15］的启发，本文将构建以下Hilbert 型不等式

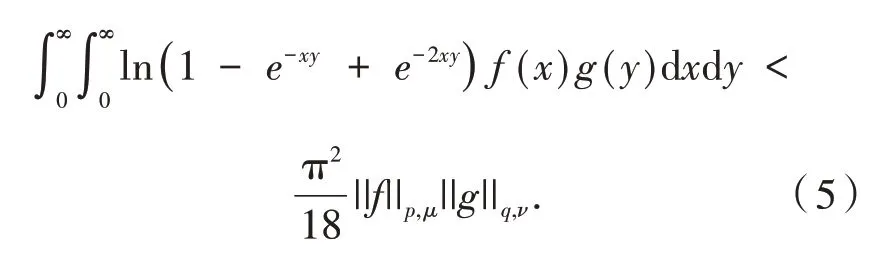
其中：μ(x)=x-1，ν(y)=y-1及

其中：μ(x)=xp-1，ν(y)=yq-1.更一般地，下文将构造一个含有对数函数及指数函数的多参数核函数，并同时考虑齐次和非齐次两种形态，利用统一的处理方法，建立式（5）及式（6）的统一推广.先给出以下引理.

1 预备知识

引理1 设b＞a＞0，γ＞0，定义K(t):=则

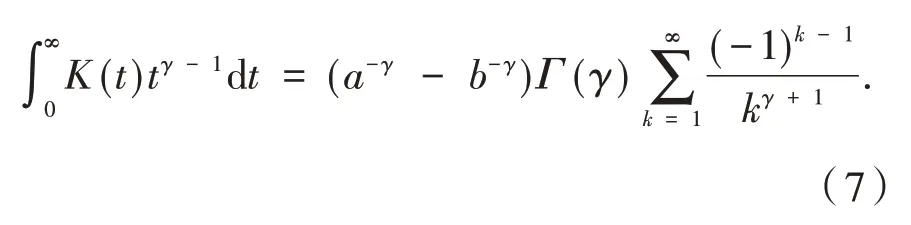
证明 把ln(1 +e-at)展开为麦克劳林级数，并逐项积分，可得

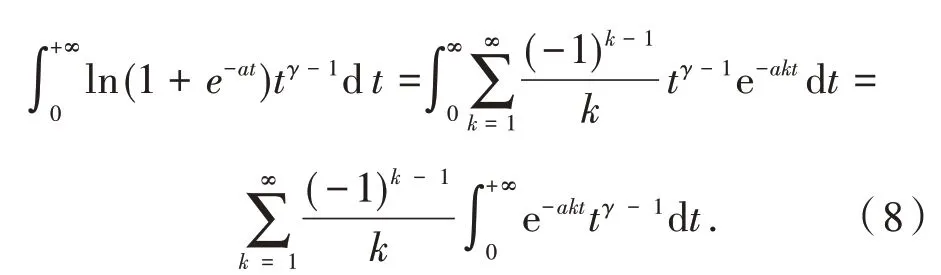
作代换u=akt，则

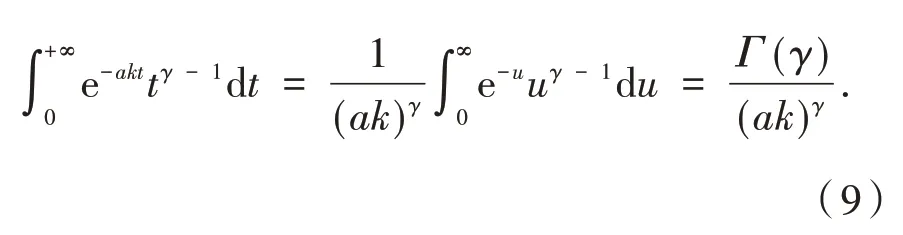
把式（9）代入到式（8），可得

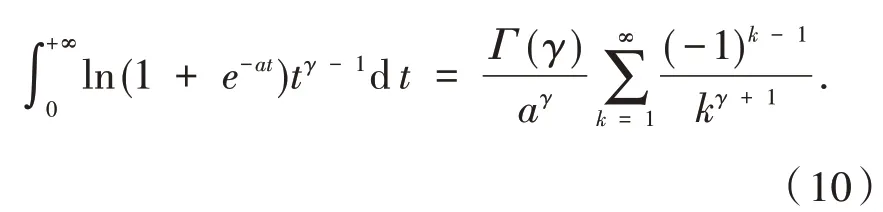
类似地，可算得

结合式（10）与式（11），可得式（7）.

引理2 设b＞a＞0，K(t)如引理1 定义，则

证明 任取δ1，δ2＞0，经过简单的代换，可得

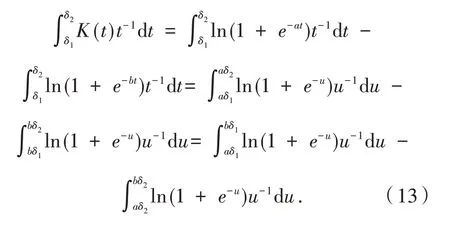
分别对式（13）中的积分使用积分第一中值定理，则有

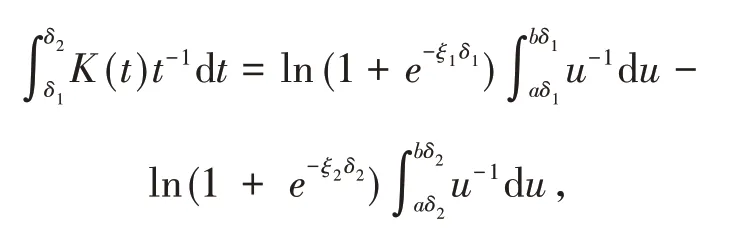
其中：a＜ξ1，ξ2＜b，令δ1→0，δ2→+∞，则可得式（12）.

注：根据引理1 和引理2，可记

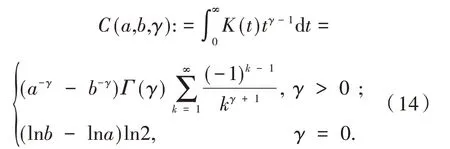
引 理3 设b＞a＞0，γ≥0，β1β2≠0，由式（14）定义.定义核函数

n∈N+，且fn(x)及gn(y)定义如下：

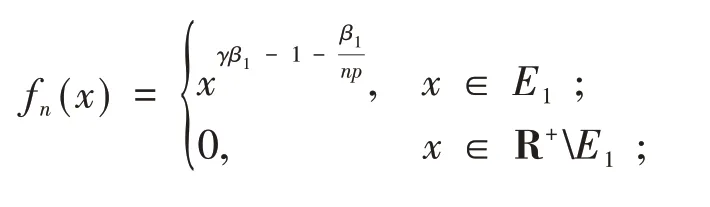
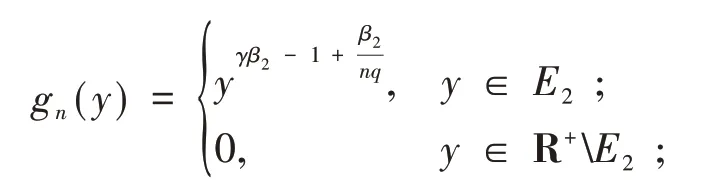
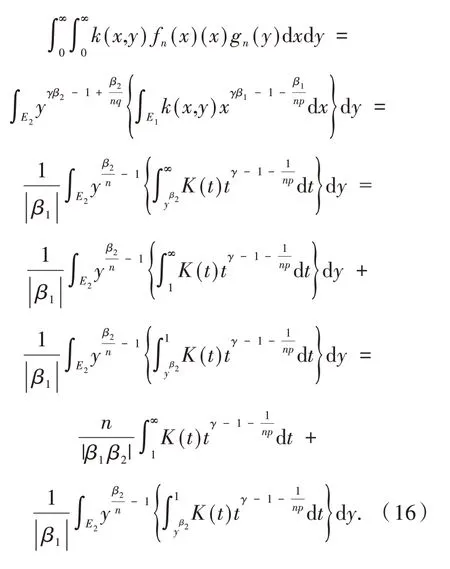
不管β2＞0 还是β2＜0，由勒贝格控制收敛定理，可算得

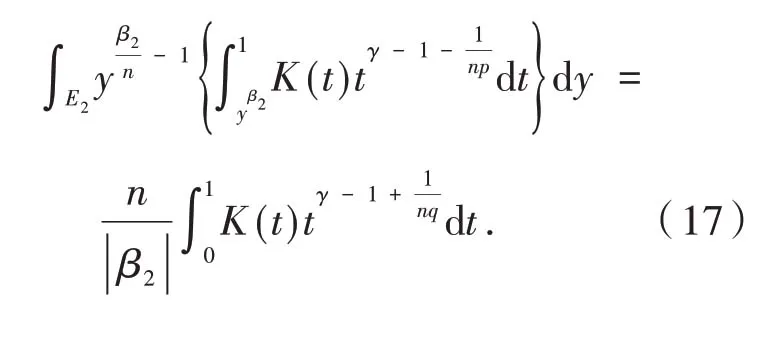
把式（17）代入到式（16），令n→∞，并利用式（14），则可得式（15）.

2 主要结果

定 理1 设b＞a＞0，γ≥0，β1β2≠0，和k(x,y) 分别由式（14）和 引 理3定义且 满 足f∈Lp,μ(R+)，g∈Lq,ν(R+)，则

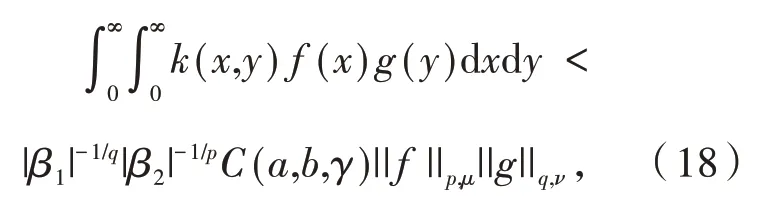
证明 由Hölder 不等式［16］，得

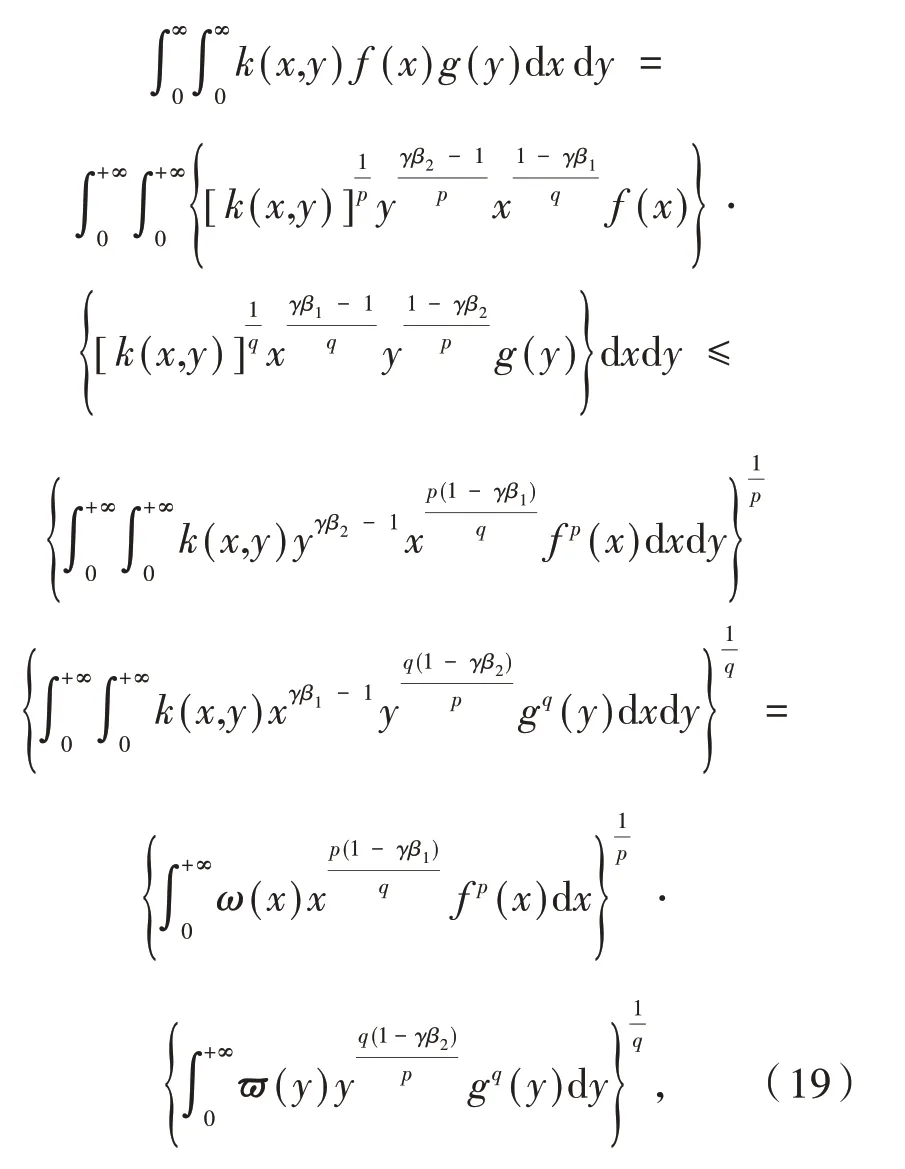
类似地，

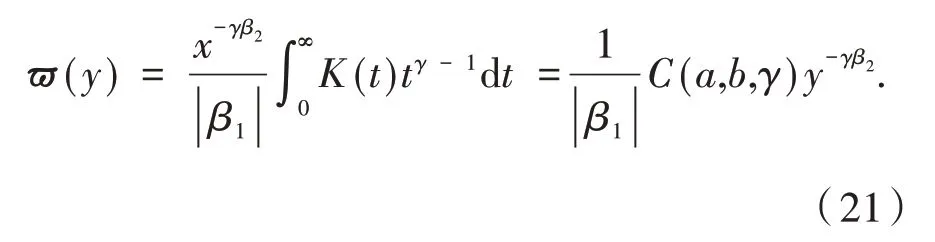
将式（20）和式（21）代入式（19），则有

根据Hilbert 不等式相关文献［2-3］通用的处理方法，可得式（22）不可取等号，故式（18）成立.

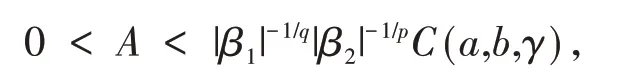
使得式（22）的常数因子变为A后，式（22）依然成立.即

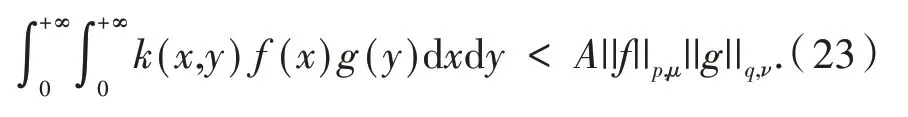
用引理3 中的fn(x) 和gn(y) 分别替代式（23）中的f(x)和g(y)，并借助式（15），可知

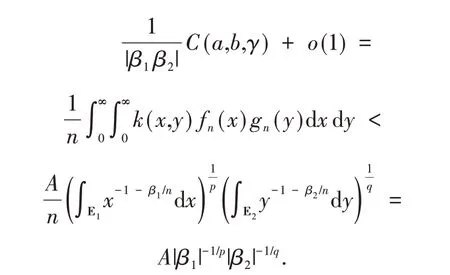
令n→∞，则这显然与假设矛盾.故式（22）的常数因子最佳．定理1 证毕.

在定理1 中，令β1=β2= 1，γ= 1，因

故定理1 转化为：

其中：μ(x)=x-1，ν(y)=y-1.令a= 1，b= 3，则有式（5）成立.

在定理1 中，令β1=β2= 1，γ= 3，因

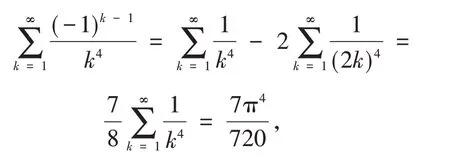
故定理1 转化为：

在定理1 中，令β1=β2= 1，γ= 0，a=1，b= 2，则有式（6）成立.另外，在定理1 中，令β1= 1，β2= -1，还可得0 齐次核的Hilbert型不等式，在此不再赘述.

3 结语

通过构造一个与指数函数和对数函数相关、且包含齐次和非齐次两种情形的核函数，建立了一个新的Hilbert 型不等式.核函数中引入β1和β2这两个实数域中的参数，对之前文献中参数的范围有所改进，处理方式也异于以往；在最佳常数的处理上，借助积分第一中值定理等分析的方法，解决最佳常数的计算问题.