一类具有时滞的分数阶SIS 模型的稳定性分析

蒲武军

近年来，随着计算机技术的不断发展，分数阶计算引起了许多学者的关注，并已经成功应用到许多工程技术领域［1-2］，特别是许多应用数学工作者正在用分数阶计算模拟现实过程［3-5］.HETHCOTE 讨论了一类经典的传染病模型［6］.CHEN 讨论了该模型格动力系统行波解的存在性［7］.郑义讨论了该模型在分数阶导数意义下各类平衡点的稳定性［8］.然而，传染病有一定的潜伏期.如新冠肺炎部分个体潜伏期达14 天之久.因此，讨论具有时滞的分数阶传染病模型具有十分重要的意义［9-10］.基于此，本文考虑如下具有时滞的分数阶传染病模型.

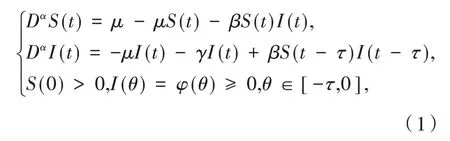
其中：α(0＜α≤1)是方程（1）的阶数，S(t)，I(t)分别表示易感者和感染者在时刻t时占总人口的比例，β称为日接触率，μ表示单位时间内人口的常数输入率，γ表示疾病的恢复率，τ表示疾病的潜伏期.

1 预备知识

定义1［11］设α∈R+，函数f(x) ∈L1(0,t)，t＞0，则 函数f(x)的α阶Riemann-Liouville 分数阶积分定义为：

定 义2［11］函 数f(x) 的α∈(n- 1,n) 阶Caputo 分数阶导数定义为：

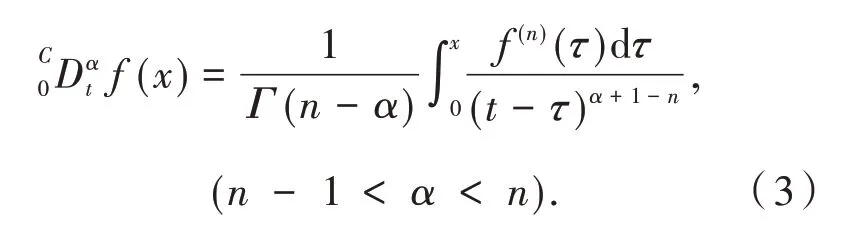
引理1［12］考虑下面具有Caputo 分数阶导数的非线性微分方程

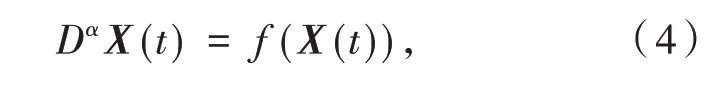
其中：α∈(0,1]，X(t) ∈Rn，则系统（4）的特征方程为|sαE-A|= 0.A为函数f(X(t))在系统（4）的平衡点处的雅可比矩阵.若特征方程限制在-π＜arg(s) ≤π 内的所有特征根均具有负实部，则系统（4）的零解局部渐近稳定.特别地，令sα=λ，则上式变为|λE-A|= 0.此时系统（4）的平衡点局部渐近稳定的充要条件为

引理2［13］考虑下面具有Caputo 分数阶导数的非线性时滞微分方程

其中：α∈(0,1],X(t) ∈Rn,τ≥0，则系统（5）的 特 征 方 程 为|sαE-A-Be-sτ|= 0.A，B分别为函数平衡点f(X(t))和g(X(t))在系统（5）的平衡点处的雅可比矩阵.若特征方程限制在-π＜arg(s) ≤π 内的所有特征根均具有负实部，则系统（5）的零解局部渐近稳定.

2 主要结果

2.1 平衡点与基本再生数

由系统（1）的第一个方程可知，当疾病不存在时，随着时间的变化该地区的总人口数量最终趋于1.因此系统（1）的任意解将进入或停留在区域D中，其中

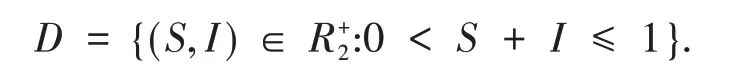
区域D是系统（1）的正不变集.显然系统（1）总存在一个无病平衡点E0(1,0).利用下一代生成矩阵的方法可得基本再生数R0=

定理1 若R0＞1，则系统（1）存在唯一的地方病平衡点E*，若R0＜1，则系统（1）不存在地方病平衡点.

证明 显然，系统（1）的地方病平衡点E*应满足如下方程组

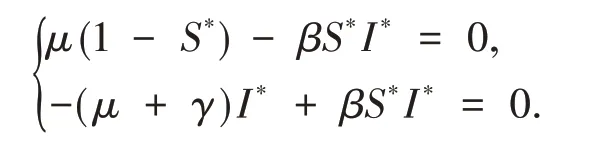
2.2 解的存在性与非负性

定理2 对任意的(S0,I0) ∈Ω，则系统（1）存 在 唯 一 解X= (S,I) ∈Ω，其 中 Ω={(S,I) ∈R2:max{|S|,|I|} ≤K}.

证明 定义映射f(X)= (f1(X),f2(X))，其中

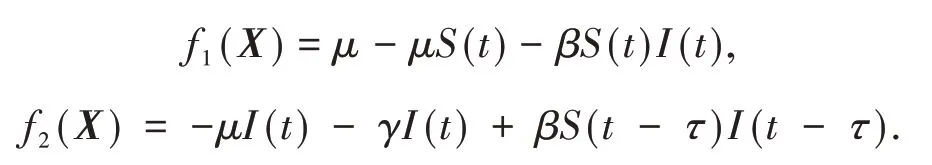
对

因此，f(X)关于X满足Lipschitz 条件，由文献［14］的定理3.7 易知系统（1）存在唯一解X(t).

定理3 系统（1）任意始于D的解是非负的.

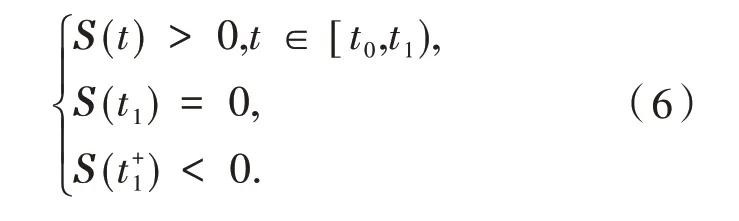
由式（6），并结合系统（1）的第一个方程，易知DαS(t1)|S(t1)=0=μ.根据文献［15］的定理1 易 得这 与矛 盾.因 此，S(t) ≥0,∀t≥t0.同理可证∀t≥t0，I(t) ≥0.

2.3 无病平衡点的稳定性分析

系统（1）在无病平衡点E0处的雅可比矩阵为：

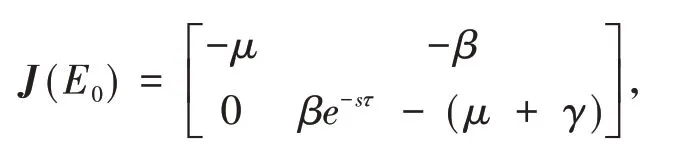
其相应的特征方程为：

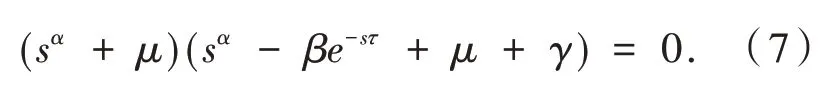
当τ= 0 时，方程（6）简化为：

定理4 若R0＜1 时，则当τ= 0 时，系统（1）的无病平衡点E0是局部渐近稳定的.

定理5 若R0＜1 时，则对任意的τ≥0，系统（1）的无病平衡点E0是局部渐近稳定的.

证明 若R0＜1 时，则定理4 成立.注意到式（7）的第一个方程不含时滞τ，因此只需考虑第二个方程

当τ≠0 时根的分布情况即可.设方程（9）存在一对纯虚根s1,2=±iw，将其代入方程（9），得

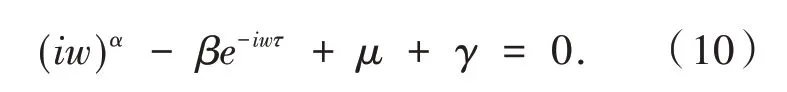
分离实部与虚部得

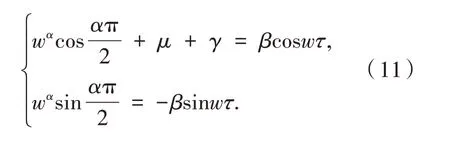
将式（11）两端平方相加，得

显然，若R0＜1 时，则方程（12）无正根，即特征方程（9）不存在纯虚根.结合定理4 及特征根关于时滞的连续性知，当R0＜1 时，对任意的τ≥0，系统（1）的无病平衡点E0局部渐近稳定.

2.4 地方病平衡点的稳定性分析

系统（1）在正平衡点E*处的雅可比矩阵为：

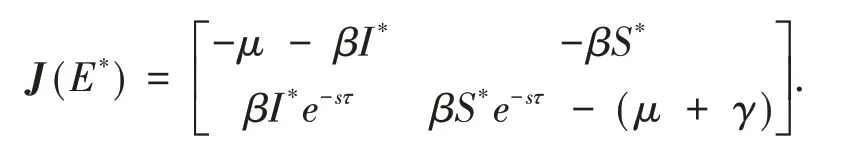
于是，系统（1）在E*处的特征方程det(J(E*))= 0 可写为：

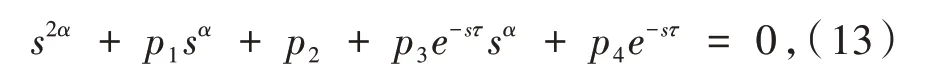
定理6 若R0＞1，则对∀τ≥0，系统（1）的地方病平衡点E*局部渐近稳定.

证明 若R0＞1，根据定理1 知地方病平衡点E*存在.当τ= 0 时，方程（13）简化为：

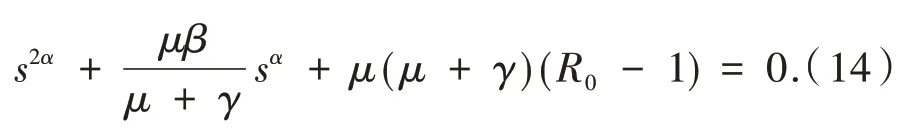
由霍尔维茨判据和引理1 知，系统（1）的地方病平衡点E*局部渐近稳定.

若τ＞0，假 设是式（13）的一对纯虚根，并代入式（13），得|ω|2α(cosαπ +isin(±απ)) +|ω|α(μ+

分离实部和虚部，有

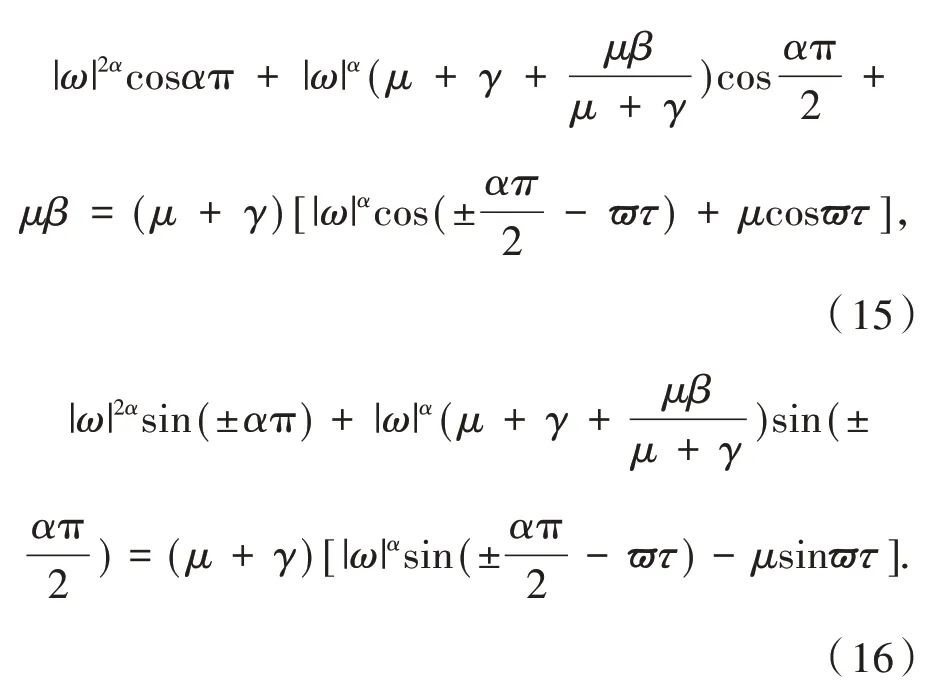
将上面二式平方相加可得

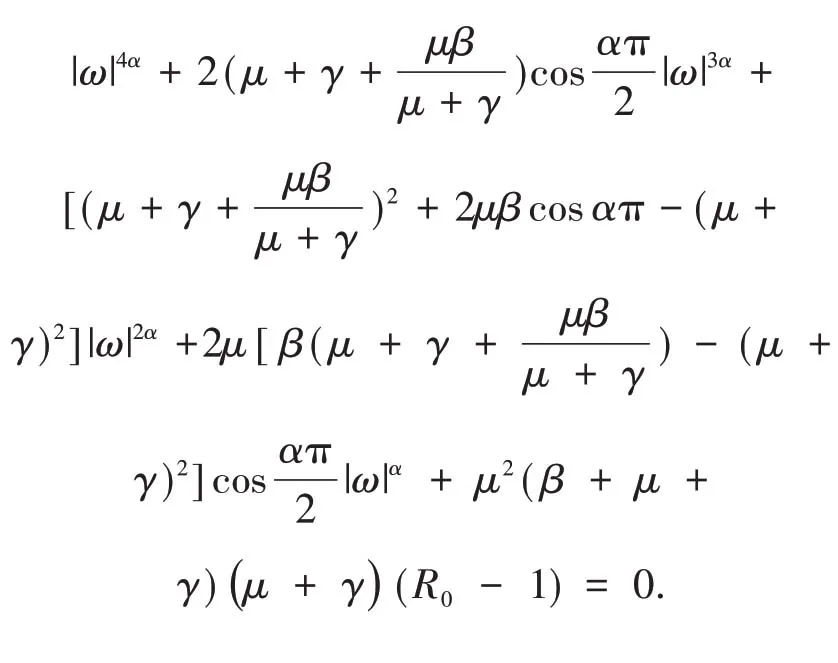
记

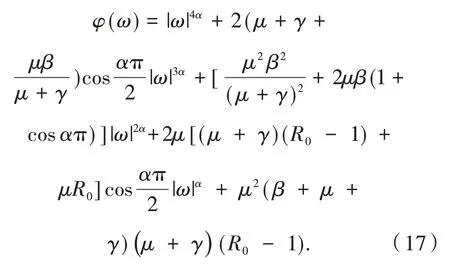
显然，若R0＞1，则方程φ(ω)= 0 不存在纯虚根，于是对任意的τ≥0，由文献［16］中引理1 和性质3，知地方病平衡点E*局部渐近稳定.

2.5 无病平衡点的全局渐近稳定性分析

定理7 若R0＜1，则对∀τ≥0，系统（1）的无病平衡点E0全局渐近稳定.

计算L0(t)沿着系统解的关于时间的分数阶导数

因此，若R0＜1，则DαL0(t)≤0，当且仅当S= 1,I=0时，DαL0(t)= 0.

设M= {(S,I) ∈D|DαL0(t)= 0}.当t→+∞时，M→{E0}所以{E0}是M唯一最大正向不变集，由Lasalle［17］不变原理知，系统（1）的无病平衡点E0在D中全局渐近稳定.

3 结语

本文主要讨论了一类具有时滞的分数阶传染病模型的动力学行为，包括该模型解的存在唯一性、非负性，无病平衡点的局部渐近稳定性和全局稳定性，地方病平衡点的局部渐近稳定性，结果显示时滞不会对该地方病平衡点的局部渐近稳定性产生影响.