转子叶尖间隙对风扇气动特性及单音噪声特性影响的数值计算
2020-12-21王良锋乔渭阳杨党国
王良锋, 杨 野, 乔渭阳, 杨党国
(1.中国空气动力研究与发展中心 空气动力学国家重点实验室, 绵阳 621000;2.中国空气动力研究与发展中心 高速空气动力研究所, 绵阳 621000;3.西北工业大学 动力与能源学院, 西安 710072)
0 引 言
由于叶尖泄漏流对叶轮机内部流场具有显著的影响,研究人员对其特性进行了深入的研究分析,例如Inoue和Kuroumaru[1],Storerand Cumpsty[2],以及Lakshminarayana等[3],他们指出叶尖泄漏流具有三维非定常特性,对叶轮机气动性能有较大的影响。宾夕法尼亚大学在1.5级低速涡轮实验台上对转子叶尖间隙内流场结构进行了大量的实验测量研究,探索叶尖泄漏流动损失产生机理,极大促进了叶轮机叶尖间隙流动方面的研究[4-9]。但是,这些研究主要分析了叶片通道内涡流场与气动性能的关系,而没有分析涡流非定常特性对噪声的影响。
目前环境保护要求的不断提高,叶轮机噪声问题已经成为社会关注的焦点,也成为世界民用航空领域竞争的一个焦点,而且在航空产品竞争力上扮演着越来越重要的角色。经过几十年的努力,采用传统的叶轮机降噪设计技术能够继续降低叶轮机噪声的潜力已经不大。要进一步降低叶轮机噪声,必须对叶轮机进行精细化的气动声学设计,并且发展创新型的降噪技术。这都强烈依赖于叶轮机关键设计参数对气动性能和噪声辐射强度影响的精细化研究。本文的主要目的即为研究不同叶尖间隙尺寸对轴流风扇气动性能和单音噪声辐射强度的影响。
相比于在气动方面的工作,叶尖间隙对叶轮机噪声影响的研究要少得多,而且主要研究其对宽频噪声的影响。Kameier和Neise[10]指出,叶轮机转子叶尖反流是一个重要的噪声来源。Fukano等[11]利用随转子旋转的热线探针研究了叶尖间隙流动产生的噪声,研究结果指出,尽管间隙流本质上是一种宽频噪声源,但是噪声频谱上出现了峰值频率,而且该峰值频率随着转速的增加而增大,当转速恒定时,该峰值频率随流量的增加而增大。NASA格伦研究中心的Hughes等(2005)[12]实验研究了不同叶尖间隙下风扇的气动性能和气动噪声的变化,实验结果表明,叶尖间隙对风扇噪声的影响比较复杂,其与风扇工况以及风扇结构类型都密切相关。Alessandro Corsini等[13]在管道风扇上研究了转子叶尖平板设计的降噪效果,该设计方案不仅可以改善转子气动性能,而且还能够降低转子噪声。赵磊[14]利用CFD和CAA混合模型研究了叶尖间隙对涡轮单音噪声的影响,研究结果表明:对于转/静干涉而言,叶尖间隙会增大涡轮单音噪声,但是对于静/转干涉而言,叶尖间隙会降低涡轮单音噪声。但是由于硬件条件的限制,他仅仅研究了叶尖间隙对涡轮后传1BPF单音噪声的影响。
从上述分析可知,关于叶尖间隙对风扇噪声的影响,大部分的研究集中于叶尖间隙对噪声辐射强度的影响,并没有深入分析叶尖间隙对声源分布特性的影响,也没有考虑噪声频率和传播方向的影响。本论文将以某单级高速轴流风扇为研究对象,利用开发的流场/声场混合模型[15]研究转子叶尖间隙对风扇气动性能、不同传播方向和不同频率单音噪声辐射强度以及声源分布特性的影响,分析转子叶尖间隙对风扇单音噪声的影响机理。
1 研究对象及计算设置
1.1 研究对象
该风扇计算模型如图1所示,该风扇包括24个转子叶片和36个静子叶片。表1给出了该风扇模型的主要设计参数。

图1 风扇级计算模型
1.2 网格划分
为了保证对风扇内部流场的准确模拟,同时尽量降低计算量,数值模拟采用的计算域包括2个转子叶片和3个静子叶片,如图2所示。该计算域的子午流面示意图如图3所示。
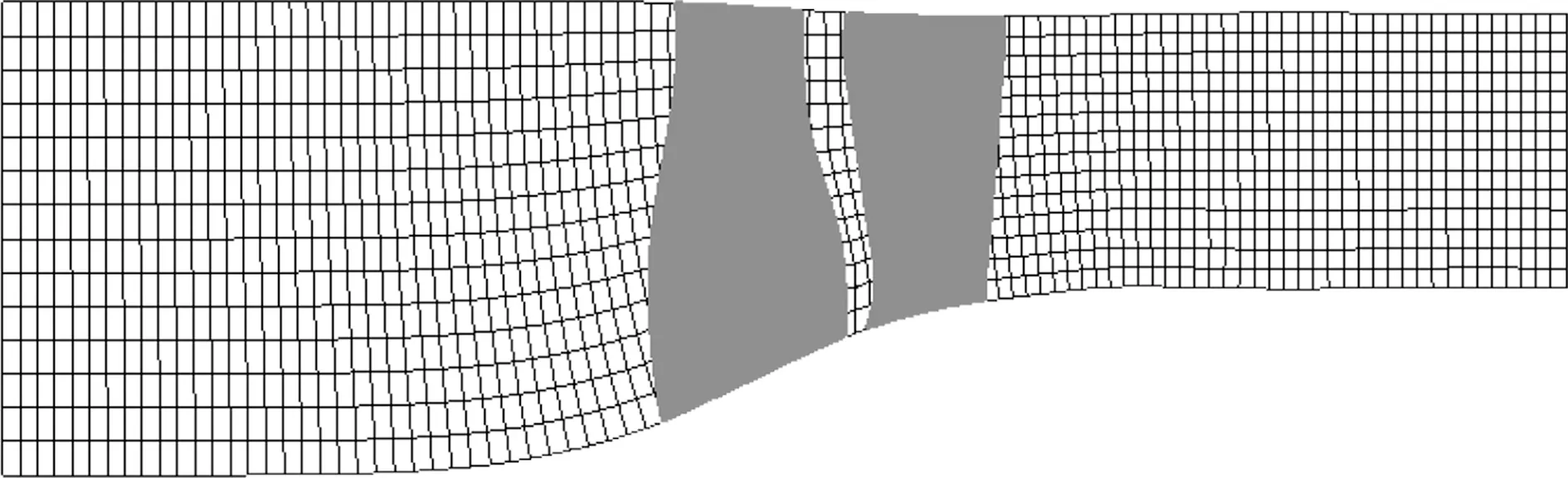
图3 计算域子午面示意图
1.3 数值计算方法及边界条件设置
数值计算中控制方程采用有限体积法求解,空间离散采用了高阶差分格式,时间离散为二阶向后欧拉差分格式。数值计算中选用基于k-ω模型的SST(Shear-Stress-Transport)湍流模型。进口边界给定总温、总压和气流方向,出口给定静压边界条件。
非定常计算中物理时间步长设置为Δt≈5.952×10-6s,即转子叶片转过一个叶片通道的时间步为60步,计算7圈共168个叶片周期后,各个监控值均呈现周期性的波动。该数值计算方法可以准确模拟叶轮机的气动性能及中尺度流场时空发展[16-17]。
1.4 网格无关性验证
数值模拟之前进行网格无关性验证不仅可以降低数值离散引起的误差,而且还可以在保证计算精度的情况下选择最少的网格量(降低计算量)。数值模拟分析了3套网格量对风扇特性的影响,3种网格设置方案都采用相同的网格拓扑结构,差别只在于网格密度不同。在网格量无关性验证中,转子叶尖间隙设置为0。表2给出了网格量无关性的验证结果。
从表2可以看出,当计算域网格量增加到250万时,风扇的流量、总压比和等熵效率变化很小,因此,计算域网格量至少保证在250万以上。根据叶轮机械气动声学基本理论可知,风扇单音噪声是转子叶片尾迹周期性地扫过下游静子叶片引起的,准确捕获静子叶片表面压力脉动信息对风扇单音噪声预测至关重要。因此,风扇转子叶片表面网格划分保证第一层网格的无量纲高度y+<5,而静子叶片表面网格划分保证第一层网格的无量纲高度y+<1。在保证叶片表面y+满足上述要求的情况下,计算域最终的网格量为300万以上。

表2 网格量无关性验证结果
1.5 研究对象管道声模态分析
根据管道声模态理论[18-19]可以得到该风扇在计算状态下不同频率的单音噪声对应的截通模态数(如表3所示)。从表3中可以看出,对于1BPF而言,m=-12是离散单音的主要周向模态,其中包括n=0和n=1两个径向模态;在2BPF和3BPF下,由于频率的提高,使得处于“截通”的模态数也随之增加。
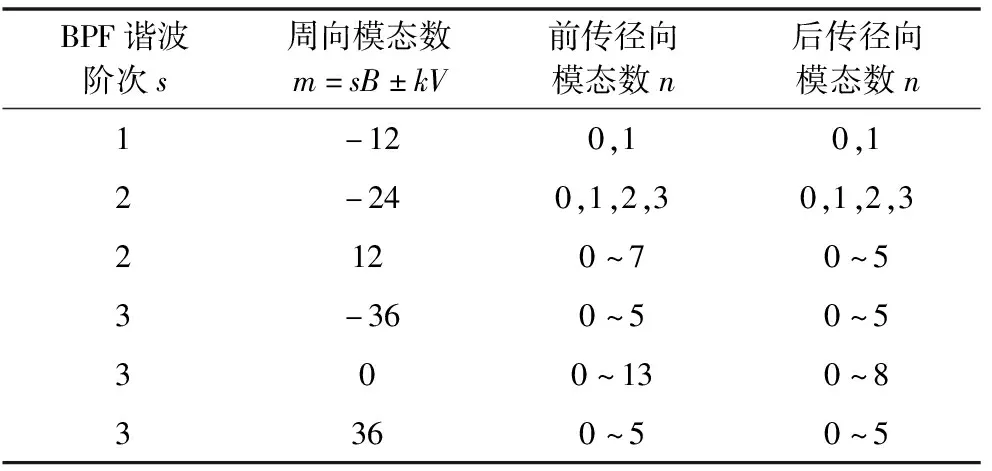
表3 研究对象管道声模态分析(B=24,V=36)
2 流场/声场混合模型
流场/声场混合模型是将叶轮机非定常流场数值模拟结果与管道内Goldstein方程[20](即声类比方程)有效耦合,实现对叶轮机单音噪声的模拟。
对于亚声速叶轮机械而言,忽略单极子声源项和四极子声源项,管道内声压计算方程为[21]:
exp(imφ-iγmnx1)
(1)
其中p是声压,pmn是对应频率下(m,n)阶模态的振幅,Ψmn是管道特征函数,κmn是管道模态特征值,m是周向模态阶数,n是径向模态阶数。
混合模型中,下游叶片表面周期性的压力脉动信息被用来作为声源信息来计算管道内的声场强度,该信息是直接通过CFD计算获得。然后,由管道声学理论就可以计算出pmn,最终得到对应的声功率:
(2)
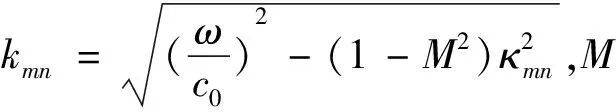
流场/声场混合模型能够准确模拟叶轮机单音噪声,实现对叶轮机单音噪声基本规律的分析和认识[15,22-23]。
3 叶尖间隙对风扇气动性能的影响
论文研究了6种转子叶尖间隙高度的情况,分别是0 mm、0.5 mm、1 mm、1.5 mm(约1%叶高)、2 mm和2.5 mm。
3.1 叶尖间隙内网格层数无关性验证
间隙内网格保证机匣和叶片顶部第一层网格y+<5,按比例向间隙内扩展。在叶尖间隙内,由于流场的局部速度梯度很大,所以必须保证其展向和周向足够的网格数。在叶尖泄漏流动影响区域内,只有足够的网格层数才能保证准确捕获叶尖间隙内的流动结构[14,24-25]。图4给出了25%弦长位置和75%弦长位置处叶尖间隙内不同网格层数计算得到的间隙内速度分布图,可以看到,要准确捕获间隙内的流动结构,间隙内网格层数至少要15层以上。在本节算例中,2 mm和2.5 mm间隙高度设置30层网格,其他间隙设置20层网格。最终,整个计算域网格数在340万以上。
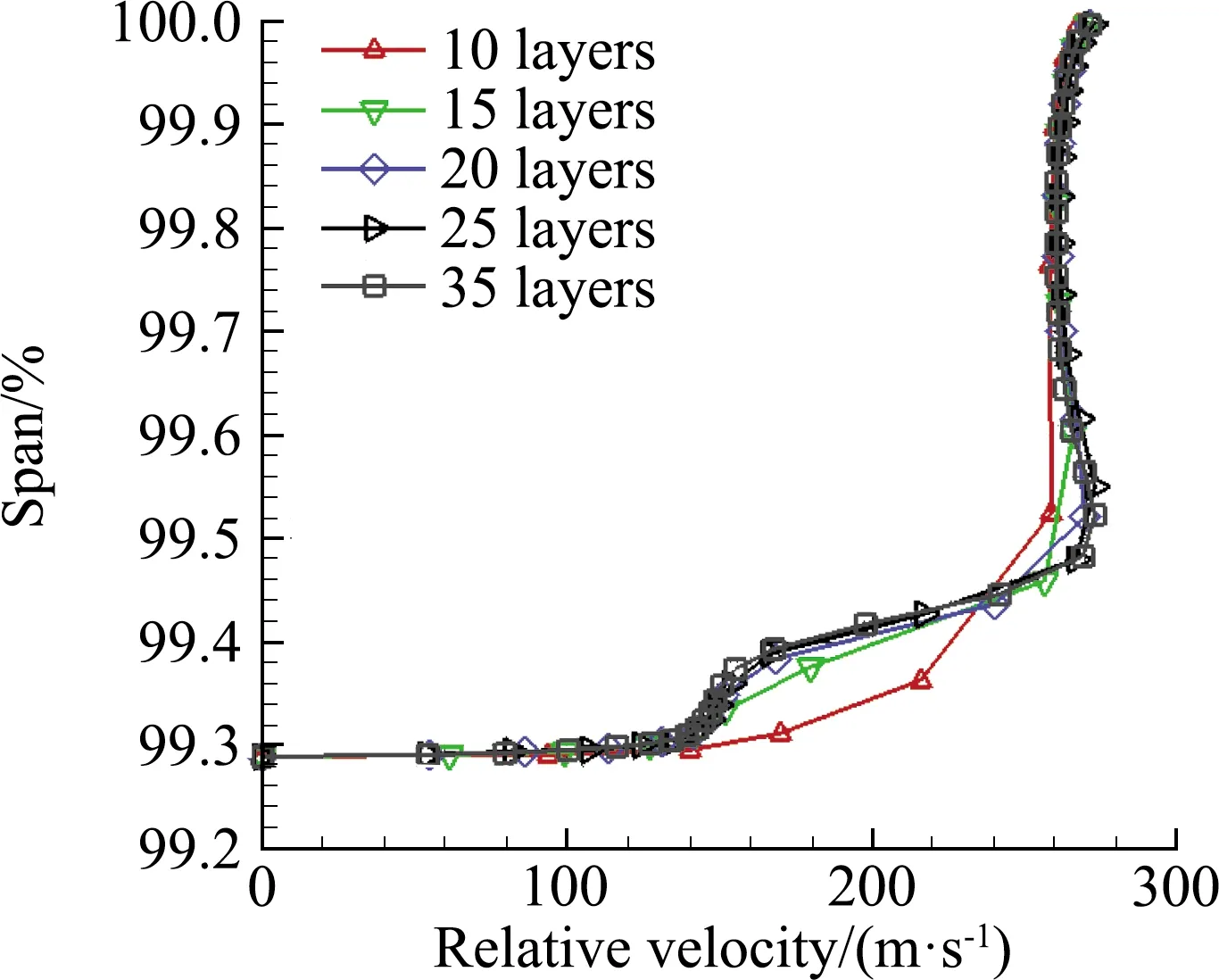
(a)25%弦长位置
3.2 叶尖间隙对气动性能的影响
表4给出了不同叶尖间隙条件下定常和非定常时均流量、等熵效率和总压比的比较。可以看到,随着风扇叶尖间隙的增大,风扇流量减小,效率降低,而总增压比减小不明显。2.5 mm间隙使得风扇流量减小了约2%,风扇效率较无间隙时下降约1%。
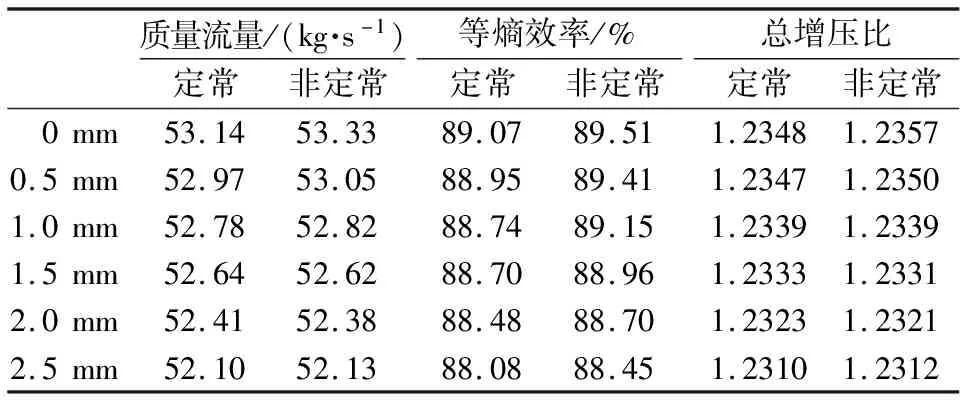
表4 不同叶尖间隙条件下风扇气动性能比较
图5给出了风扇50%展向位置总压瞬态总压分布云图,从图中可以看出数值模拟可以清晰地捕获转子尾迹与下游静子叶片之间的相互干涉。从风扇单音噪声的产生机制来看,上游尾迹特性(包括强度、宽度和相位分布)直接影响风扇单音噪声强度。图6给出了不同叶尖间隙情况下风扇转子出口时均相对速度的分布云图。从图6中可以看出,随着叶尖间隙的增大,尾迹分布沿展向的变化范围也随之增大,但是即使当叶尖间隙增大到2.5 mm时,转子出口尾迹特性发生变化的范围也主要集中在86%以上的展向范围内。我们将重点分析86%以上展向位置的尾迹变化。
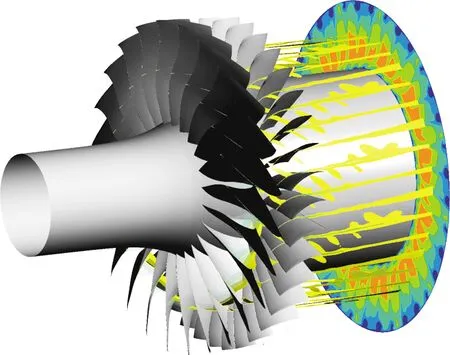
图5 50%展向位置和风扇级出口平面瞬态总压分布云图

(a)0 mm TC
图7给出了90%和98%展向位置处转子出口相对总压的周向分布。转子间隙带来的叶尖二次流导致转子出口尾迹宽度和尾迹强度都有不同程度的增大,而且间隙越大,尾迹宽度和尾迹强度的幅值也越大。前人的研究已经指出,这两个因素对单音噪声强度有不可忽视的影响。另外,转子叶尖间隙对尾迹相位分布没有明显的影响,当尾迹与下游静子叶片干涉时,仅仅影响静子叶片表面的非定常载荷强度,而不会影响其相位分布。

(a)90%展高位置
4 叶尖间隙对风扇单音噪声的影响
使用URANS/DBAA单音噪声预测模型可以对不同转子叶尖间隙下风扇单音噪声进行计算分析。表5和表6分别给出了不同间隙高度下向前传播和向后传播的风扇单音噪声声功率级。可以看到,不论是向前传播还是向后传播的单音噪声,随着叶尖间隙的增大,1BPF下的噪声级是随之增大的。2.5 mm间隙使得向前传播的1BPF单音噪声声功率级增大了1.5dB,向后传播的1BPF单音噪声声功率级增大了0.7dB。但是2BPF和3BPF下的单音噪声强度随叶尖间隙的变化较为复杂,没有特定的规律,而且变化幅度都小于1dB。总的来说,对于该风扇级而言,转子叶尖间隙对单音噪声的影响主要集中在1BPF上,对2BPF和3BPF的单音噪声影响很小。
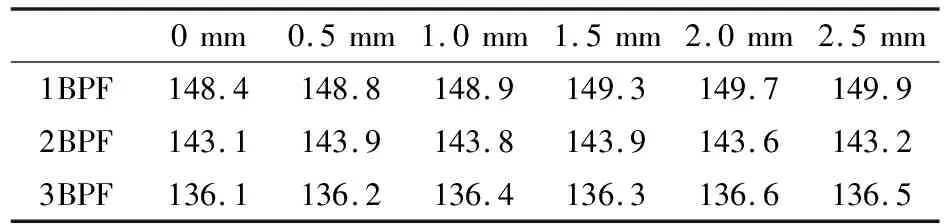
表5 不同间隙高度下风扇单音噪声PWL比较(向前传播)
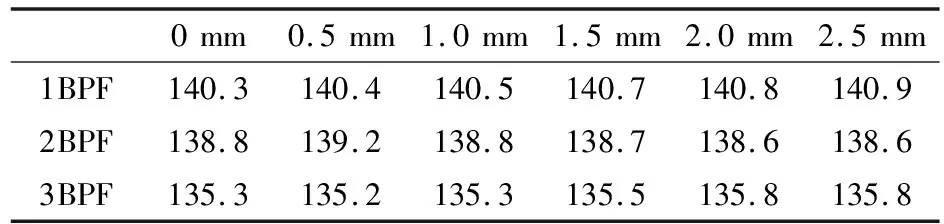
表6 不同间隙高度下风扇单音噪声PWL比较(向后传播)
某个频率下的声功率是将该频率下所有“截通”模态的声功率进行叠加得到的,而有些情况下我们会关心各个模态各自的声功率强度,因此,图8~图10分别给出了不同频率下单音噪声各个模态的声功率级分布图。由于叶尖间隙对不同模态声功率上的分配影响很小,因此,这里仅给出了TC=0 mm时的模态声功率图。需要指出的是图中只给出了处于“截通”状态的模态声功率级。从图中可以看出,对于风扇进口噪声和出口噪声,尽管在模态结构上大体相同(主要是“截通”的径向模态阶数不同),但是两者在各个模态的能量分配上差异很大,而且处于“截通”状态的模态个数也不相同,这主要是由于风扇进出口几何参数和气动参数不同引起的。
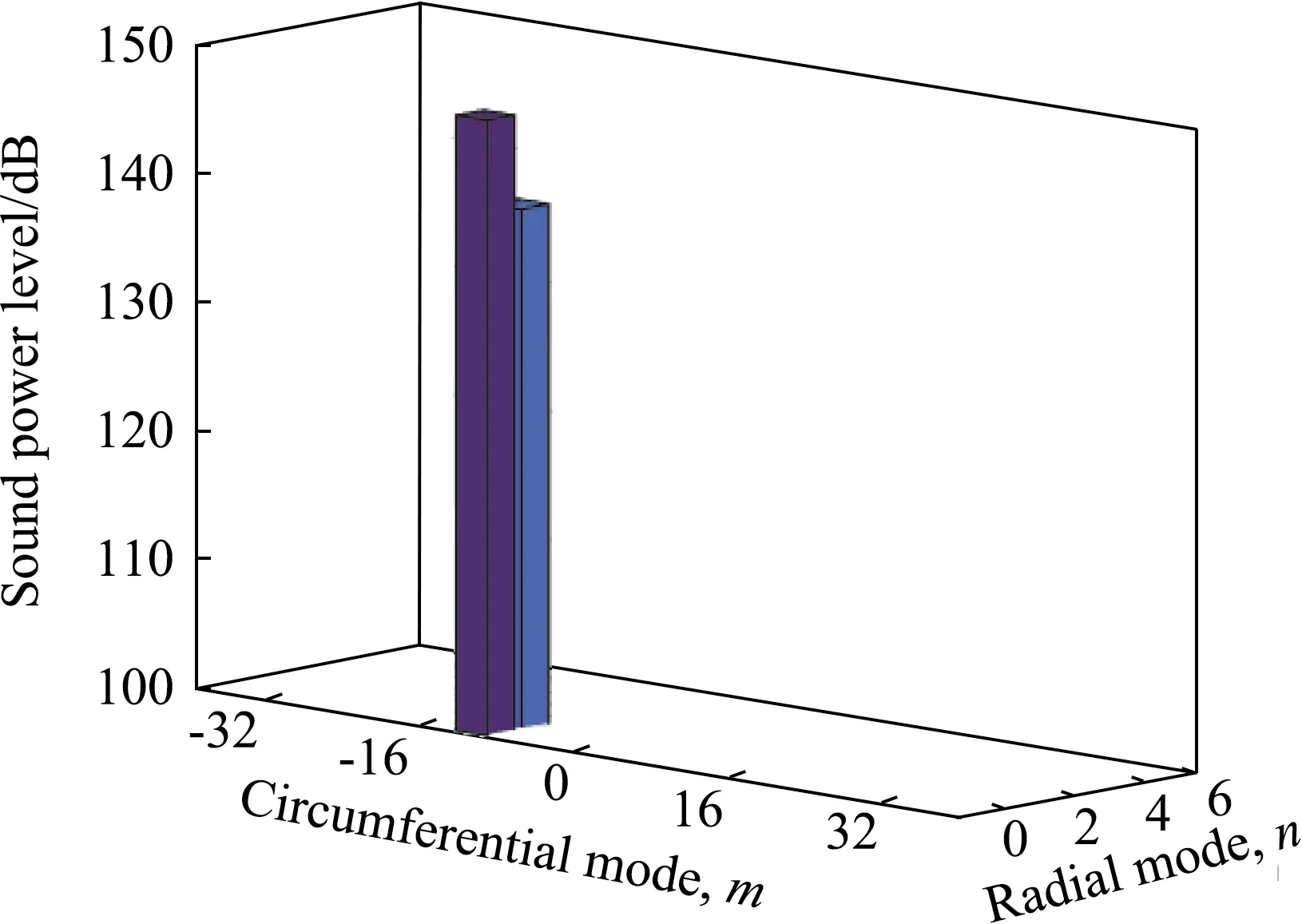
(a)向前传播

(a)向前传播

(a)向前传播
图11~图13分别给出了TC=0 mm时静子叶片压力面1BPF、2BPF和3BPF对应的脉动压力幅值分布。可以看出,对于单音噪声而言,静子叶片前缘始终是压力脉动幅值最大的区域,这与风扇单音噪声产生机制是相符的。从图中还可以看到,静子叶片前缘并不是唯一的主要声源区域,对于1BPF对应的脉动压力而言,静子叶片压力面80%以上展向位置都是较为明显的声源区域,尤其是在尾缘附近形成图11中的“A”区域,其脉动压力幅值与前缘位置接近;对于3BPF对应的脉动压力而言,静子叶片压力面65%~75%展向位置附近(图13中的“B”区域)也形成了显著的声源区域。
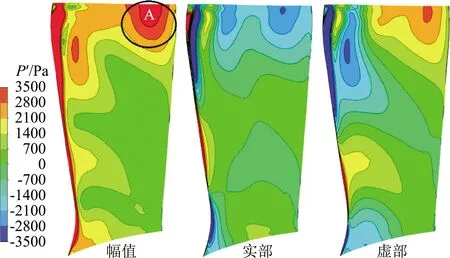
图11 静子叶片压力面非定常压力载荷分布(1BPF)

图12 静子叶片压力面非定常压力载荷分布(2BPF)

图13 静子叶片压力面非定常压力载荷分布(3BPF)
为了研究在“A”区域产生高压力脉动幅值的原因,图14给出了80%轴向弦长平面上的瞬态静压分布和尾迹位置分布。可以看出,在该时刻,位于中间的静子叶片“A”区域,压力面静压达到最大值,而对应的吸力面位置静压正好是最小值,这样就会导致“A”区域成为重要的声源区域。“B”区域成为3BPF下非定常压力脉动幅值较大的区域,其产生原因也可以使用相似的方法进行分析。

图14 80%轴向弦长平面熵和静压分布云图(后视图)
另外,从图11中静子叶片表面非定常压力脉动实部或者虚部的分布图中可以看出,叶片前缘复数振幅沿展向相位变化了2次,说明上游一个转子尾迹将同时与两个静子叶片相互干涉。为了验证这一结果,图15给出了静子叶片上游熵的瞬时分布图,从图中可以很直观地看出,同一时刻,上游一个转子尾迹可以与下游两个静子叶片相互干涉,这与图11的结果是相符的。

图15 静子叶片前缘附近平面瞬时熵分布云图(前视图)
图16给出了不同叶尖间隙条件下静子叶片表面1BPF对应的脉动压力幅值分布。从图中可以看出,转子叶尖间隙变化对下游静子叶片表面非定常载荷分布的影响主要集中在80%展高以上的叶尖区域,对其他区域影响不大。在静子叶片吸力面上,叶尖间隙主要影响图中的区域“A”和区域“C”,区域“A”位于叶片前缘附近,而区域“D”位于叶片尾缘附近。随着叶尖间隙的增大,区域“A”和区域“C”的脉动幅值都明显增大,而且这里的区域“A”与图11中的区域“A”是相同的。总体上来说,转子叶尖间隙增大主要影响静子叶片压力面上的非定常压力脉动分布,对吸力面上的非定常压力脉动分布影响很小。可以看到,随着转子叶尖间隙的增大,下游静子叶片吸力面上只有很小区域(图中的区域“D”)上的非定常压力脉动幅值随之增大。
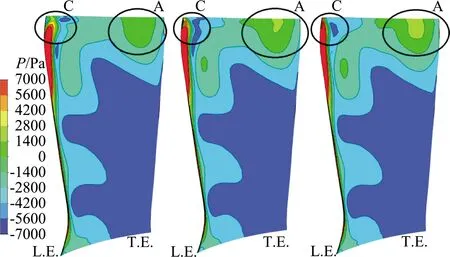
(a)压力面
5 结 论
1)风扇转子叶尖间隙增大,减小了风扇流量,降低了风扇等熵效率,但是对风扇总增压比影响很小。相比于无间隙而言,2.5 mm的叶尖间隙使得风扇流量减小了约2%,风扇效率较无间隙时下降约1%。
2)转子叶尖间隙主要影响85%以上展向范围内的尾迹强度和尾迹宽度,对相位分布影响很小。在相位分布不变的情况下,尾迹强度和尾迹宽度的增大会导致单音噪声辐射强度的增大。因此可以通过对比不同叶尖间隙下转子下游尾迹特性的变化,定性分析其对单音噪声辐射强度的影响。
3)转子叶尖间隙对风扇单音噪声辐射强度及声源分布特性的影响与传播方向和声波频率密切相关,并且主要影响1BPF单音噪声的辐射强度,而对高次谐波噪声的辐射强度影响较小。
