基于意义联结，助推思维进阶

刘霞

一、思维生长点：从计数走向计量，几何直观支撑计数单位到计量单位的转换

三年级学生的思维能力处于从具体到抽象过渡的初期，也是思维进阶的转折点，此时几何直观更有利于学生进行知识的关联沟通。设计如下的对比体验素材，让学生经历关联教学过程，锻炼思维能力。

【题组1】

问题：一共有多少个鸡蛋？（图略）先估一下，再写出算式，用竖式帮助解答。

追问1：为什么列出乘法算式？

追问2：摆竖式的时候，先算的是什么，再算的是什么？（竖式略）

追问3：结合图形说一说你对这个乘法算式意义的理解。

追问4：13、22分别表示什么，286表示的是什么？

追问5：3×22=66和10×22=220分别表示什么？请在图上圈出来，并说一说。

【题组2】

问题：这个盒子的面积是多少？（图略）请写出算式，并借助竖式解答。

追问1：为什么列出乘法算式？

追问2：摆竖式的时候，先算的是什么，再算的是什么？（竖式略）

追问3：你能结合图形说一说对这个乘法算式意义的理解吗？

追问4：一个小正方形的面积是多少？13指的是什么？22指的是什么？286表示的是什么？

追问5：3×22=66和10×22=220分别表示什么？请在图上圈出来，并说一说。

对比追问：不变的是什么，变的是什么？

两份对比素材，分别是点状的鸡蛋图和面状的格子图。每份素材设计相似的问题，每个问题都承载了各自的设计意图。追问1：倒逼学生思考乘法的意义和本质，从乘法意义的角度进行思考，一个是计数单位的累加，一个是计量单位的累加，都是求积的过程。追问2：从意义出发关联算理。追问3：被动思维呈现，评价学生的理解程度。追问4：对比体验，一个表示的是计数单位的个数，一个表示的是计量单位的个数，建立知识的关联点。追问5：深度挖掘竖式计算在不同情境中所承载的不同意义。对比追问：在思考变与不变中，体验计数到计量的联结点。

上述问题的引导要达成两个层次的目标。第一层次：乘法运算意义与算理的进一步理解沟通;第二层次：体验变与不变。不变的算式，变的是单位和具体问题承载的意义。从熟悉的计数问题到不熟悉的计量问题，让知识找到生长的土壤，促成思维在沟通关联中发展。

二、思维拔节点：从意义走向图式，任务驱动探究两位数乘两位数的分与合

思维的发展是纵横交错展开的，在纵向打通计数和计量的联结点后，横向拓展练习恰是思维生长的拔节点。首先设疑“这个图式你可以看懂吗”（图1），给学生锻炼思维的空间。承接此任务，再设计三个层次的探究性任务。

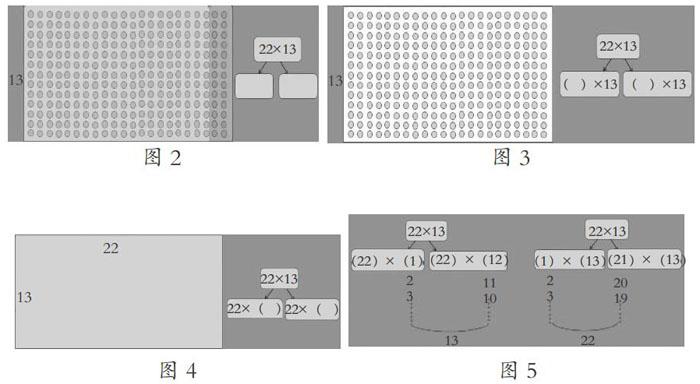
第一层次，操作载体为点状鸡蛋图，设计两个问题，先是由图到式（图2），讓学生从图上去发现一个乘法算式基于意义可以分成哪两部分。再由式到图（图3），让学生主动构建分的方法，然后在分的基础上，得出分的图式。两个问题承载不同的思维含量。第二层次，操作载体为面状长方形图（图4），从点状图到面状图，问题虽然一样，但思维层次有着很大的跨越。第三层次，操作载体为抽象的图式，意在培养学生们的抽象概括能力。抛出问题“你能有序地对这个算式分一分吗？”（图5）从图到式，再图式联合，最后到抽象的图式，这样的进阶让学生的思维有所倚靠又有所发展。

从第一次以鸡蛋图为载体的点状探究到以长方形为载体的面状探究，再到基于图式的抽象概括，学生经历了从模型初探、模型再探到模型建立的过程，是一次深度学习的过程。

三、思维绽放点：从图式走向问题，问题解决疏通两位数乘两位数的意义

高阶思维的养成需要训练学生思维的灵活性和敏捷性。具体表现为能迅速地对具体问题做具体分析，采取灵活的方法来思考问题。本课后续教学以前面的图式分解为基础，在意义思辨、图式思辨和批判思辨中，培养学生形成解决问题的策略，达成思维的绽放。

问题：欣欣农场里有一片蔬菜种植区，它的长和宽刚好是1、2、6、8四个数字组成的两个两位数，且这两个两位数的乘积最小，请帮忙找到它的长和宽。

意义思辨：基于乘法意义或是乘法算式乘积的特点，可以得出两种可能，分别为16×28和18×26。

师：请想一想，第一步我们要做什么？可以得到什么？

生1：可以根据乘法的意义，先把最小的数字放在十位，另外的两个数字分别放在个位，然后再计算比较。

生2：也可以根据我们前面探究的规律——和相等，差越小，积越大。

这一环节考查学生们是否养成遇到问题逐步思考的好习惯。学生根据乘法算式的意义想到第一步对策，先将两个最小的数字1和2，分别放在两个数的十位。

图式思辨：在乘法意义深刻建构的基础上，结合图形对两个算式分别进行分解，判断出乘积的大小。

问题：16×28、18×26两个算式乘积的大小，不借助竖式计算，可以判断出它们乘积的大小吗？

师：请观察格子图中的两个图形，比较16×28、18×26两个算式乘积的大小，并完成填空。（格子图略）

直接将两组数据对应的图形画在格子图中，留给学生足够的思考时间，让他们先根据图形得出结论，再来完成分一分，降低他们思考的难度。此环节要让学生们通过观察格子图得出，两个长方形有一部分是重叠的，所以只要比较未重叠部分就可以得出结论。接着，再引导学生完成从格子图到算式的分解，使图与式对应（图6，格子图略），让算理与算法融合。

批判思辨：两个数的和不相等时，不能基于“周长相等，长和宽相差越小面积越大”的规律得出答案，但基于乘法意义进行分解的方法可行。

问题：欣欣农场计划建造一个游乐区，有两种方案，请你帮忙选出面积最大的方案。方案一为长72米，宽33米;方案二为长71米，宽34米。

师：这题还能用规律解决吗？试试看。

师：可以用什么方法解决？（方法如图7所示）

从周长相等到周长不等，培养学生借助学过的知识，批判性地思考问题，不拘泥于固定的形式和结论。三次思辨，三次成长，在问题链的引导下，促成学生的高阶思维在不断思辨中成长。

（作者单位：浙江省杭州市富阳区灵桥镇中心小学本专辑责任编辑：王彬）