BaBiO3电子结构与机械性能的第一性原理研究

刘 林， 王殿辉， 钟 燕， 胡朝浩

(桂林电子科技大学 材料科学与工程学院,广西 桂林 541004)

目前，作为一种新型高温超导材料，BaBiO3吸引了科研人员的广泛关注。BaBiO3存在单斜、菱方和面心立方结构，并可以发生相转变。在常温状态下，BaBiO3以单斜I2/m相存在，当温度达到425 K时，单斜I2/m相转变成菱方R-3相，直到温度达到893 K时再次发生相变，转变为面心立方结构[1]。早期，科研工作者在BaBiO3中加入钾元素，发现可以形成具有高于30 K超导温度的化合物Ba1-xKxBiO3[2]。由于该化合物中Bi具有+3和+5的混合价态而产生的电荷歧化，极有可能是获得高温超导的原因[3]。BaBiO3具有三维的Bi-O阵列结构，与传统的铜基超导体二维片层结构完全不同。Tang等[4]的研究表明，BaBiO3中Bi原子存在+3、+5价，且这2种价态的Bi原子对光催化性能的贡献不同。鉴于此，为了探明BaBiO3的超导机理和光催化性能，开展研究Bi混合价态的工作是必不可少的。为此，运用第一性原理计算了BaBiO3三种相的电子结构，并在此基础之上通过用钽(Ta)掺杂BaBiO3改变电子能带结构和BaBiO3机械性能，为今后该材料的实验提供理论依据。

1 计算方法

BaBiO3与Ta掺杂BaBiO3的电子结构和力学性能均在VASP软件包[5]中完成。原子核与电子的交互作用采用投影缀加波法(PAW)[6-7]来描述，交换关联能采用perdew-burke-ernzerhof(PBE)修正的广义梯度近似(GGA)来处理[8]。为了得到精确的晶体结构，对初始结构进行充分的驰豫，其截断能设置为520 eV，采用不大于2π×0.03 Å-1的k点网格密度。在优化过程中，当能量的收敛度小于1×10-5eV，且每个原子受力小于0.01 eV/Å时，结构优化完成。为了快速准确地得到计算结果，在整体计算过程中，用费米形式的展宽模式来计算电子态密度。

2 结果与讨论

2.1 BaBiO3的晶体结构

表1为BaBiO3三种相的优化晶格常数，图1为经过结构优化后BaBiO3的立方、菱方、单斜相晶体结构。3种晶相的BaBiO3由BiO6八面体结构组成，其中Bi原子位于八面体中心，O原子位于八面体各顶角。在BiO6八面体结构单元中，由于Bi原子以+3和+5混合价态存在，导致出现2种Bi—O键键长。八面体与八面体之间通过共享一个O原子相连接，并形成电子传输通道。

表1 BaBiO3三种相的优化晶格常数

图1 BaBiO3的晶体结构

在立方和菱方的结构中存在2种不同的Bi—O键长，在—Bi—O—Bi—O—Bi—键所形成的平面上，O原子的排列具有疏密性偏离Bi原子的现象，这个现象从电荷密度图中也可以观察到[10]。BaBiO3三种结构优化前后Bi—O键长的变化列于表2中，其中Bi(I)表示+5价Bi原子，Bi(II)表示+3价Bi原子。从表2可看出，BaBiO3面心立方结构和菱方结构在结构优化前后，2种Bi—O键长差均发生改变，面心立方中Bi—O键的键长差减小到0.041 3 Å，但在菱方结构中反而增大到0.158 0 Å。对于单斜结构来说，优化前后Bi—O键的键长变化较为复杂，八面体中的Bi—O键长不相等。从表2可看出，存在2种不同长度的Bi—O键，较长的Bi—O键长为2.32 Å，而较短的Bi—O键长约为2.17 Å。一个八面体中的Bi—O长键通过顶角的O原子与紧邻的八面体中的Bi—O短键互连。由于键长的方向依赖性产生对应的电荷方向依赖性，导致了单斜结构的产生。值得注意的是，光生电子空穴的传输，光催化性能和材料的各向异性均受这种特性的影响。

在单斜结构对称的体系中，存在一种Bi—O“breathing distortion”(呼吸形变)模式[11]，这种模式不是普遍存在的，而是由单斜结构八面体中Bi原子电荷的歧化造成的。在表2中的实验数据[9]展示了这2类八面体的呼吸形变为同一八面体中不同类型Bi-O的差值，即为0.000 3 Å和0.008 5 Å，与本次计算值0.003 7 Å和0.009 1 Å基本相符。由此可表明，这种呼吸模式影响催化剂的催化性能、自身相结构或者晶面的性质。如BiVO4单斜结构的光催化性能在3种结构中最高；另外，在BiVO4和金红石TiO2的各个晶面中，(110)面的氧化能力最强。

表2 具有不同对称性结构的BaBiO3键长分布 Å

2.2 BaBiO3的电子结构

在得到优化结果的基础上，进一步计算了BaBiO3的能带结构和电子态密度。对于DFT计算，往往只关注靠近费米能级附近的几条能带。BaBiO3三种晶体结构的能带结构如图2所示。

图2 BaBiO3三种不同晶体结构的能带图

相关BaBiO3立方结构的实验结果表明，其为间接半导体，但测得的带隙值差别较大，变化范围在0.2～2.0 eV[12-16]。由于在正常的DFT计算中未考虑电子的激发效应，计算结果一般比实验值偏小。从图2(a)可看出，因面心立方结构的BaBiO3的带隙被低估，导致了价带与导带重叠。BaBiO3菱方和单斜结构分别在高对称点L、V处为最小带隙，被低估后的带隙分别为0.20、0.05 eV，且与BaBiO3的立方结构一样，均为间接半导体。

为了更深入地研究BaBiO3的电子结构，以BaBiO3立方结构为例进行电子态密度分析。Bi(I)为+5价，Bi(II)为+3价的立方结构BaBiO3态密度图如图3所示。从图 3可看出，BaBiO3的电子态密度贡献主要分布在3个区间，在-1～0 eV区域的态密度主要由Bi(II)—6s、O—2p及少量的Bi(I)—6p组成。在0～2 eV附近电子态密度的主要有Bi(I)—6s、Bi(II)—6p、O—2p及少量的Bi(I)—6p、Bi(II)—6s组成。在能量大于2.5 eV的区间电子态密度主要由Ba—5d、Bi(I)—6p、Bi(II)—6p、O—2s及O—2p组成。由于Bi(I)和Bi(II)在离子状态下电荷量不同，2种Bi原子在费米能级附近的区间分布也不同。Bi(I)因为与O—2p形成σ反键态，所以产生了Bi5+离子。此时Bi(I)—6s轨道无电子占据，为空轨道，所以Bi5+离子分布于费米能级之上的占据态；同样，Bi(II)中的6s与O—2p形成σ成键态，因此产生了Bi3+离子，分布区间在费米能级以下。从图2(a)可看到一条贯穿费米能级的能带，这是由费米能级附近Bi—6s和O—2p杂化效应造成的。

图3 立方结构BaBiO3态密度图

2.3 Ta掺杂BaBiO3的电子结构

具有典型ABO3型钙钛矿结构的BaBiO3由2种不同价态的Bi原子周期性排列，形成明显的层状结构。对于50% 的Ta掺杂，由于周期性中心和棱占位，中心和面心的位置是完全等效的。也就是说，沿a、b、c轴中任意方向移动晶格长度的一半，得到的掺杂模式能带结构与移动前是一致的，能带图如图4(a)所示，带隙约为2.66 eV。 若不考虑BaBiO3的对称性，则只在同一个层状结构中替换Bi而掺入50%的Ta原子。这样仅保证了该掺杂结构具有50% Ta的掺杂量。该结构破坏了原有的周期性，导致该掺杂模型的能带结构中价带与导带相交，表现出金属性，如图4(b)所示。因此，掺杂Ta的位置对材料本身的性能影响较大。

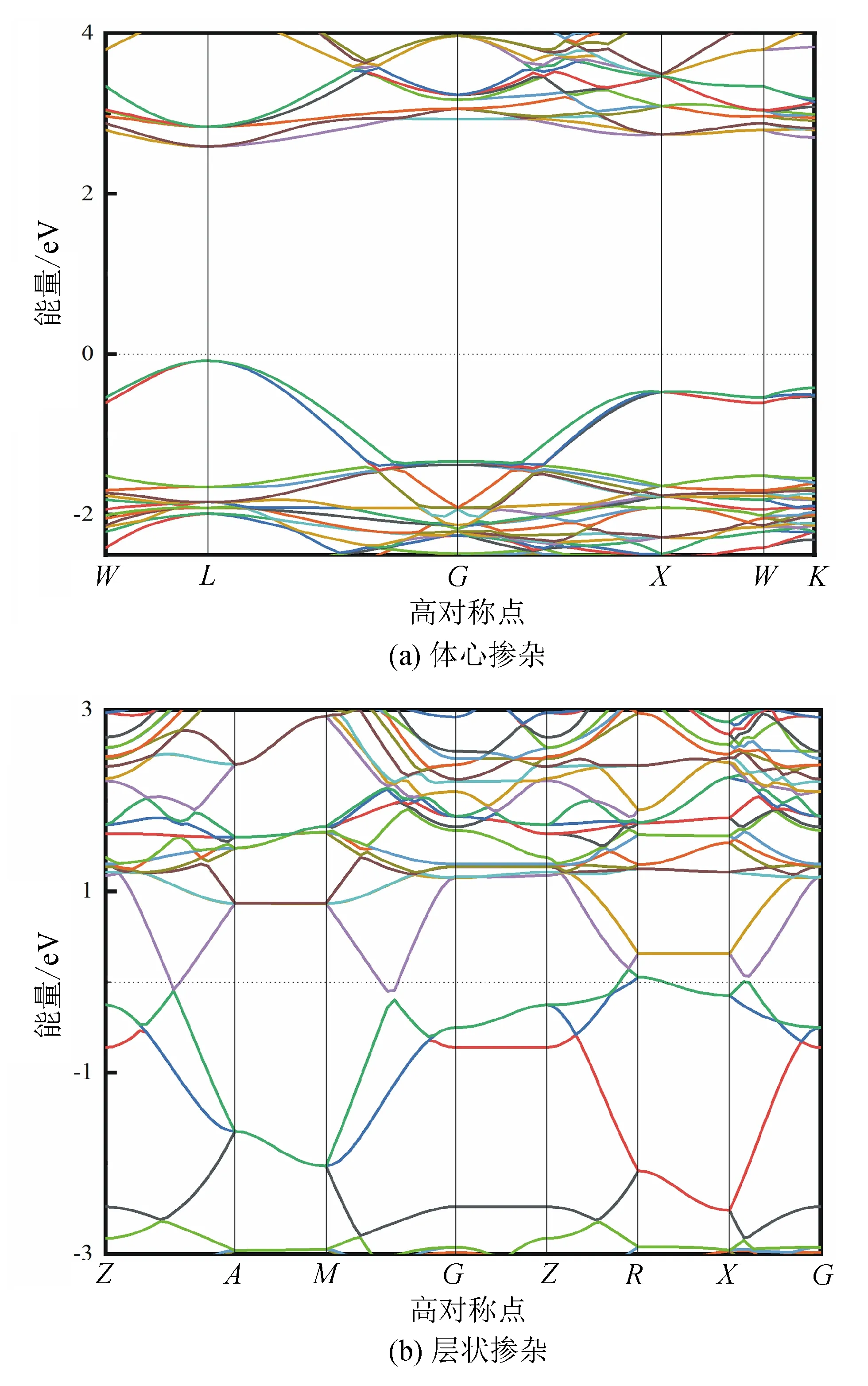
图4 Ta替换Bi掺杂浓度为50%的BaBiO3能带结构

当Ta替换Bi的掺杂浓度为12.5%时，Ta的掺杂在面心立方的体心、面心或者棱中点时的能带结构是一致的，如图5(a)所示。因为晶格的对称性，该掺杂浓度下，不管是体心掺杂模型，还是面心掺杂模型、棱掺杂模型，都可以通过沿着晶格轴平移来相互转换。例如，体心掺杂移动a/2的长度就会转换为面心掺杂模型，然而整个晶格的对称性却未发生变化。通过观察能带结构可发现，价带与导带相交，表现为半金属特征。与纯相BaBiO3的能带结构相比，12.5% Ta掺杂的能带结构中，使低能带的离域性和高能空带的定域性都获得了加强。由此可推断出，从纯相BaBiO3开始不断提高Ta的掺杂浓度，直到浓度达到12.5%的这个过程中，费米能级附近能级较低的能带会向高能级方向移动。掺杂浓度为37.5% Ta的情况与此浓度情况类似，所有掺杂模型的能带结构完全相同，如图5(b)所示。

图5 Ta替换Bi掺杂浓度分别为12.5%、37.5%的BaBiO3能带结构

通过掺杂方式的不同，研究了2种不同的25% Ta掺杂模型。一种用Ta原子在面心立方中的面上替换2个Bi原子，掺杂后的结构如图6(a)所示；另一种掺杂方式是使用Ta替换面心立方中一个面心Bi原子和一个体心Bi原子，结构如图6(b)所示。从图6可看出，2种掺杂结构均表现出金属性，掺杂结构中的Bi具有混合价态，仍能出现Bi的电荷歧化现象。从能带结构还可分析出，采用合适的能级修正，在图6(a)中的高对称点A和图6(b)中的高对称点G均可能出现直接带隙。

图6 Ta替换Bi掺杂浓度为25%的BaBiO3能带结构

对使用Ta替换Bi不同浓度的掺杂后，能带结构计算结果表明，仅有不破坏对称性的50% Ta会显示出明显带隙，其他12.5% Ta、25% Ta和37.5% Ta的3种浓度掺杂后均无带隙，表现出金属性。另外，从能带结构可看出，能带越过费米能级后，未发生严重的交叉。这2种现象可能是由混合价态(+3，+5)的Bi原子电荷歧化导致的。为了进一步探究其本质原因，利用杂化泛函对能带进行了修正，但依然由于Bi原子电荷的歧化现象，处理仍比较困难。

2.4 BaBiO3的力学性质

BaBiO3具有立方、三方(菱角形式)、单斜3种不同的晶系，其对应的独立弹性常数的个数也不尽相同。其中立方晶系具有3个独立的弹性常数，计算结果如表3所示。对于立方晶系，相应的力学稳定性条件为：C11>0，C44>0，C11>C12，(C11+C12)>0。通过稳定性条件的验证，立方晶系BaBiO3满足上述判定条件。

表3 计算得到的BaBiO3的弹性常数Cij、体模量B、剪切模量G、杨氏模量E及泊松比υ

材料抵抗正应力的能力和抵抗剪应力的能力分别用体模量B和剪切模量G来表示。其中B/G与材料的脆性相关，若B/G>1.75，则表明该材料具有易延展性[17]。立方结构BaBiO3的B/G=1.98，表现出良好的延展性。若材料本身的各向异性比较微弱，则可以用E=9BG/(3B+G)，υ=(3B-2G)/2(3B+G)来近似求解各向同性材料的杨氏模量E与泊松比υ[18]。泊松比υ用来表示材料在形变过程中体积的改变程度，其值越小，该材料在形变过程中体积改变越大。立方结构的BaBiO3的泊松比为0.28，表明具有较好的韧性。根据泊松比υ，还可以从力学角度得到更多的成键方面的信息[19-20]。另外，根据Zener定义[21]，可用参数A来描述立方结构BaBiO3的各向异性，其中A=G1/G2，G1=C44，G2=(C11-C12)/2，当A=1时,表明该材料不具有各向异性。通过计算得到A=0.55，表明立方BaBiO3具有各向异性。另外，根据杨氏模量E与弹性柔度之间的关系，立方结构的BaBiO3的各向异性可以由E检测。立方BaBiO3的杨氏模量E的方向依赖性如图7所示。从图7可看出，立方BaBiO3具有各向异性。

图7 立方BaBiO3杨氏模量(GPa)的方向依赖性

3 结束语

利用第一性原理对BaBiO3及使用Ta替代Bi在不同浓度掺杂下BaBiO3的电子结构和力学性能进行了计算分析。计算结果表明：1)经过结构优化后，晶格常数与实验值吻合；2) BaBiO3的面心立方结构由于DFT方法对带隙的低估与混合价态Bi原子电荷歧化，使得无法观察到带隙；3)对于Ta掺杂浓度分别为12.5%、25%、37.5%、50%四种情况，仅在50%浓度下，表现出了明显的带隙。4)通过BaBiO3力学性质的计算，表明该材料在立方结构下具有良好的延展性与韧性。