求解矩阵方程AX=B的多步迭代算法
2020-12-18周昱洁彭振赟尚邵阳
周昱洁, 彭振赟, 尚邵阳
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
矩阵方程的求解是数值代数领域的重要课题之一,在工程技术、控制理论和图像处理等方面有极大的实用价值。矩阵方程
AX=B
(1)
是最简单也是研究最多的矩阵方程类型,求解方法主要包括直接解法和迭代解法2大类。Bjerhammar[1]利用矩阵的广义逆研究了该矩阵方程在一般矩阵集合中的求解问题,并给出了有解的充要条件和通解的表达式。Allwright[2]采用凸分析的方法对矩阵方程(1)在对称半正定矩阵集合中的反问题进行了研究,给出了最小二乘解存在的条件,但未给出解的具体表达式。谢冬秀[3]通过引入新的内积并应用闭凸锥逼近理论得出了该矩阵方程存在半正定最小二乘解的充要条件以及通解的表达式。文献[4-6]分别就中心对称矩阵、广义(反)对称和广义(反)自反矩阵、(反)对称正交矩阵集合对该矩阵方程进行了研究。彭亚新[7]首次利用共轭梯度算法的思想,构造了共轭残差算法求解矩阵方程(1)的一般解、(反)对称解及中心对称解等。郭孔华[8]通过构造正交投影迭代法,进一步研究了矩阵方程(1)的几种对称性解及其最佳逼近问题。在矩阵方程(1)有解的情况下,Ding等[9]参照Jacobi迭代法和Gauss-Seidel迭代法提出了一种更广义的基于梯度的迭代算法,因收敛因子μ的存在保证了算法的收敛性,但由于该基于梯度的迭代算法只使用当前迭代近似解来决定新的迭代近似解,在求解大规模矩阵方程时可能出现收敛速度缓慢的情况。
鉴于此,提出一种求解矩阵方程(1)及其最小二乘问题的多步迭代算法,即通过前m+1个迭代近似解的特定线性组合[10-14]来估计下一步迭代近似解,并证明了算法的收敛性。数值结果表明,本算法相对于基于梯度的迭代算法具有更好的收敛效果。
1 矩阵方程(1)的多步迭代算法及其收敛性
基于梯度的迭代算法[9]:给定初始近似解X0,按照迭代格式
Xk+1=Xk+μAT(B-AXk)
(2)
计算矩阵方程(1)的第k+1步迭代近似解,其中:

λmax(ATA)为对称矩阵ATA的最大特征值。
基于梯度的迭代算法是单步迭代算法,当矩阵A为列满秩矩阵时,由该算法得到的矩阵序列{Xk}收敛到矩阵方程(1)的唯一解:
X*=(ATA)-1ATB=A+B。
基于梯度的迭代算法也是不动点迭代法[14],令
g(X)=(I-μATA)X+μATB,
则基于梯度的迭代算法的迭代格式(2)可改写为
Xk+1=g(Xk)。
算法1令
f(X)=g(X)-X,
则求解矩阵方程(1)在Rn×n内的多步迭代算法为:

2)若‖f(Xk)‖F≤ε,则程序运行终止,此时,Xk即为矩阵方程(1)在Rn×n内的解;
3)令mk=min{m,k};


(3)
5)令
(4)

为了方便讨论算法1的收敛性,给出如下引理。
引理1[15]若x*为线性方程组Ax=b的解,且x*∈R(AT),则x*是线性方程组Ax=b的最小Frobenius范数解。
引理2若X*为矩阵方程AX=B的解,且X*=ATH,H为任意矩阵,则X*为矩阵方程AX=B及其最小二乘问题的最小Frobenius范数解。
设m×n阶矩阵A的奇异值分解为
(5)
其中:U=(U1,U2),U1∈Rr×m为m阶正交矩阵;V=(V1,V2),V1∈Rr×n为n阶正交矩阵;Σ=diag(δ1,δ2,…,δr)>0,r=rank(A),则X=ATH等价于X=VH。
引理3若X*为矩阵方程AX=B的解,且X*=VH,则X*为矩阵方程AX=B及其最小二乘问题的最小Frobenius范数解。
对于算法1,有如下收敛性定理。
证明由矩阵函数f(X)和g(X)的定义可知:
f(Xk+1)=μATB-μATAXk+1。
(6)

f(Xk+1)=μATB-μATAXk+1=μATB-μATA×
因此,
(7)
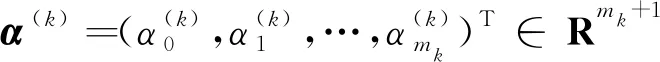
所以式(7)可转化为
‖f(Xk+1)‖F≤‖I-μATA‖2·‖f(Xk)‖F。

‖f(Xk+1)‖F≤c‖f(Xk)‖F≤…≤ck+1‖f(X0)‖F。
因此,当k→∞时,有‖f(Xk)‖F→0,f(Xk)→0,由算法1产生的矩阵序列{Xk}收敛于与矩阵方程(1)等价的法方程ATAX=ATB在Rn×n内的解。若A为列满秩矩阵,则算法1产生的矩阵序列{Xk}收敛于矩阵方程(1)在Rn×n内的唯一解A+B;若A为非列满秩矩阵,且其奇异值分解为式(5),则由算法1产生的矩阵序列{Xk}收敛于矩阵方程ATAX=ATB在Rn×n内的一个解
如何加强图书、音像、网络教学、学术、创作展演等信息资源的整合,利用教学辅助条件,满足人才培养目标;如何把教学平台、实践平台和信息平台等方面的条件有机的融合贯通,把“学校大课堂,传媒大舞台”的教学模式,融入到图书馆的工作中,就必须营造全方位的服务支撑节点,进一步深化图书馆服务,提升精准服务水平。
(8)
其中G为适当阶数的任意矩阵。矩阵方程AX=B的最小二乘解同样地可表示为式(8),则由算法1产生的矩阵序列{Xk}收敛于矩阵方程(1)在Rn×n内的一个最小二乘解。
定理2当选取初始矩阵X0=ATH,或直接令初始矩阵X0=0,则由算法1产生的矩阵序列{Xk}收敛于矩阵方程(1)的唯一的最小Frobenius范数最小二乘解X*=A+B。进一步地,若X*为矩阵方程(1)的解或其最小二乘问题的解,则有
(9)
其中,
c=‖I-μATA‖2<1。

若X*为矩阵方程(1)的解,则有ATAX*=ATB,因此有
f(Xk)=μATB-μATAXk=-μATA(Xk-X*)=
-[I-(I-μATA)](Xk-X*)。
因
‖f(Xk+1)‖F≤c‖f(Xk)‖F≤…≤ck+1‖f(X0)‖F,
其中c=‖I-μATA‖2<1,则有
(1-c)‖Xk-X*‖F≤‖f(Xk)‖F≤
c‖f(Xk-1)‖F≤…≤ck‖f(X0)‖F≤
ck(1+c)‖X0-X*‖F。
因此,有
定理3若矩阵方程AX=B有解,则由算法1产生的矩阵序列{Xk}收敛于矩阵方程(1)在Rn×n内的一个解,当选取初始矩阵为X0=ATH,或直接取X0=0时,由算法1产生的矩阵序列{Xk}收敛于矩阵方程(1)唯一的最小Frobenius范数最小二乘解为X*=A+B。若X*为矩阵方程(1)的解,则误差估计式(9)成立。
矩阵方程(1)有解时,其解的表达式与其最小二乘解的表达式相同,则与定理1和定理2一样可以证明关于算法1的收敛性定理3。
2 数值实验
数值算例中矩阵A、B均由MATLAB软件随机产生,所有数据均在Window7 64-bit MATLAB R2013a环境下获得。对于多步迭代算法1,实验中初始矩阵X0选取为零矩阵,终止准则为‖f(Xk)‖F<10-6。
例1给定矩阵A∈R7×5和B∈R7×5:
A=

B=

由于矩阵A为列满秩矩阵,矩阵方程AX=B有唯一精确解。应用基于梯度的迭代算法和多步迭代算法1均可得矩阵方程(1)在Rn×n内的唯一精确解:
X*=A+B=

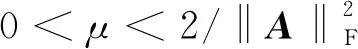

表1 基于梯度的迭代算法在选取不同收敛因子μ的数值结果

表2 多步迭代算法1在选取不同收敛因子μ和正整数m的数值结果
由表1、表2可得如下结论:

2)对于多步迭代算法1,当m=2或m=3时,其数值结果受2个收敛因子μ和m的共同影响,难以选择最佳收敛因子,当4≤m≤6时,其数值结果只受收敛因子m的影响,且m≥5时收敛效果最佳。
3)多步迭代算法的收敛性比基于梯度的迭代算法好,当2种算法的收敛因子μ取相同数值时,多步迭代算法有明显的加速收敛效果。


表3 不同矩阵维数下基于梯度的迭代算法的数值结果
由表3、表4可得如下结论:
1)随着矩阵A的规模增大,多步迭代算法的收敛性始终比基于梯度的迭代算法要好。对于同一矩阵方程,多步迭代算法有明显的加速收敛效果。
2)对于大规模矩阵方程AX=B,固定收敛因子μ,当m≥6时,多步迭代算法1的收敛效果最佳。
3)由于多步迭代算法使用前m+1个迭代近似解的线性组合,随着矩阵维数的增加,虽然加速效果依然明显,但运行时间也相对增加。因此,收敛因子m的选择并非越大越好,应根据矩阵方程的规模大小适当选取收敛因子μ和m,以达到最佳的收敛效果。
3 结束语
通过研究矩阵方程AX=B及其最小二乘问题,提出了一种使用前m+1个迭代近似解的线性组合来决定下一步迭代近似解的多步迭代算法。该算法能够使新的迭代近似解更接近原问题的精确解,从而

表4 不同矩阵维数下算法1在选取不同参数因子m的数值结果
减少迭代次数,达到更快收敛到问题的精确解的目的。数值实验验证了算法的有效性,且比基于梯度的迭代算法具有更好的收敛效果。该算法应用到其他类型的矩阵方程时的收敛效果还有待进一步研究。
