求解张量方程的Levenberg-Marquardt-型方法
2020-12-18刘奇龙段雪峰
王 丽,刘奇龙,段雪峰
(1.山东管理学院 信息工程学院,济南 250357;2.贵州师范大学 数学科学学院,贵阳 550025;3.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)


记所有的m阶n维实张量构成的集合为R[m,n]。考虑如下张量方程:

(1)


张量方程(1)本质上是一种特殊的非线性方程F(x)=0,有多种不同的求解方法[8-10]。通常可转化为非线性最小二乘问题
其中‖·‖为2-范数。求解非线性最小二乘问题常用的算法有Newton法、LM方法以及信赖域等方法、LM方法是Newton法的改进,于1944年Levenberg在文献[11]中首次提出,随后Marquardt[12]于1963年重新发现。LM方法通过引进迭代参数,克服了Jacobi矩阵接近奇异或者坏条件时Newton法所带来的困难。将应用LM-型方法求解系数为一般张量的张量方程。数值算例表明,在某些情况下所给算法优于文献[6]中的LM法。
1 LM-型方法
应用LM-型方法求解张量方程(1)。为方便讨论,首先给出如下定义和符号。


(2)
因此,张量方程(1)的解等价于下面优化问题的全局最优解,

ai1i2…im=aπ(1)π(2)…π(m), ∀π∈Πm,

ai0i1…im-1=ai0iπ(1)…iπ(m-1),∀π∈Πm-1,


通过计算可得F(x)与f(x)的Jacobi矩阵分别为:
(3)
g(x)=f(x)=J(x)TF(x)。
(4)
下面给出求解张量方程(1)的LM-型方法,见算法1。
算法1LM-型方法求解一般张量方程。
1)若k>N,则停止;否则通过式(2)、(3)和(4)计算

2)若‖gk‖<ε,则停止;否则,转步骤3。
4)若dk满足‖F(xk+dk)‖<σ‖Fk‖,则取αk=1;否则寻找αk满足如下Armijo条件:

2 收敛性证明
为了方便证明算法1的收敛性,引入局部误差界的定义及一些引理。
定义1设X*为F(x)的解集,N⊂Rn且满足N∩X*≠∅,若存在常数c>0,使得
‖F(x)‖≥c·dist(x,X*), ∀x∈N,
则称F(x)在N内有局部误差界,其中dist(xk,X*)=infyk∈X*‖xk-yk‖。
引理1[6]设F(x)与J(x)如式(2)与式(3)所示,则F(x)连续可微,且F(x)与J(x)在
N(x*,r1)={x|‖x-x*‖ 内Lipschilz连续,即存在常L1、L2>0,r1<1,使得对∀x,y∈N(x*,r1),均有 ‖F(y)-F(x)‖≤L1‖y-x‖, ‖J(y)-J(x)‖≤L2‖y-x‖。 由引理1和文献[13]可得如下引理。 引理2若xk∈N(x*,r1),则算法1产生的迭代点列{xk}收敛于张量方程(1)的解x*。 引理3[13]设{dk}为算法1得到的序列。若xk∈N(x*,r1),则存在常数c1>0,使得 ‖dk‖≤c1dist(xk,X*)。 引理4[14]设{Jk}为算法1得到的序列。若迭代点列{xk}收敛于张量方程(1)的解x*,则Jk有如下形式的奇异值分解 (5) 其中rank(Σ1)=rank(J(x*)),且rank(Σ2)≥0,Σ3=0。 定理1若初始向量x0在误差界内收敛于张量方程(1)的解x*,则算法1产生的迭代点列{xk}二阶收敛于x*。 证明利用式(5)与引理5的奇异值分解,得到当前迭代步, 其中, (6) (7) 又因为 根据引理1、引理5与式(7)可知, cL2‖xk-x*‖2= c1dist(xk+1,X*)≤‖Fk+Jkdk‖+O(‖dk‖2)≤ 对所有充分大的k,都有 根据引理4,可得 ‖dk+1‖=O(‖dk‖2)。 因此 ‖xk+1-x*‖=O(‖xk-x*‖2)。 即{xk}二次收敛于x*。证毕。 选取几个例子运用算法1进行数值实验。所有的数值实验都在配置为Intel(R) Core(TM) i5-6200U CPU @ 2.40 GHz的计算机中使用Matlab 2015b运行。选取容许误差界ε=10-5,最大迭代次数N=20。 b=(x*)m-1, 表1 比较算法1和文献[6]中LM算法的数值结果 用算法1求解一个4阶20维的一般张量方程。在局部误差界的条件下,绘制绝对误差与迭代次数的关系如图1所示。从图1可看出,算法1是二次收敛的。 图1 LM-型二次收敛可视化 算法1也可求解形如 其中x*=5ones(n,1),选取初始向量x0=2ones(n,1),用算法1求解广义的张量方程 数值实验结果见表2。该实验表明,算法1对解决一类广义三阶的张量方程是有效的。 表2 选取不同维数的广义张量方程的数值结果
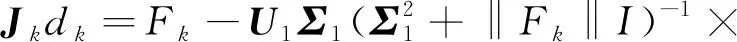

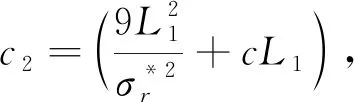
3 数值实验










4 结束语

