应用于Lamb 波的最小功率无畸变波束形成算法

褚兆飞，骆 英，秦 云

（江苏大学国家级高端装备关键结构健康管理国际联合研究中心，镇江，212000）

引 言

Lamb 波相控阵监测技术一直是板状结构健康监测研究的热点，该技术利用Lamb 波对结构中的裂纹等小损伤较为敏感这一特性，在结构中预置激励器/传感器阵列，阵列接收板中包含损伤特征信息的Lamb 波信号并对其分析解读，进而可对结构损伤实施成像监测[1]，而相控阵成像所用算法的运算效率及成像精度对最终损伤评估有着重要影响，既有超声相控阵方法多采用时域延时叠加(Delay and sum,DAS)成像算法[2‑3]，该类虽具有成像计算效率高的优点，但成像结果都会受到主瓣、旁瓣的影响，使得成像结果横向分辨率差，且存在旁瓣伪影。为此，最小功率无畸变（Minimum power without distortion re‑sponse, MPDR）自适应波束形成算法在Lamb 波损伤检测领域已得以应用[4‑7]，其相较于传统时域DAS成像算法具有成像分辨率高，可抑制旁瓣伪影的优点，然MPDR 算法在超声Lamb 波损伤检测中的应用面临诸多挑战：（1）超声Lamb 波所特有的频散特性将导致信号时域波形畸变，影响基于时域成像方法的精度；（2）自适应算法涉及谱矩阵求逆计算，直接进行求逆运算效率低，需耗费大量计算资源；（3）构成谱矩阵的有效信息量少，导致奇异矩阵无法求逆。

针对频散问题，骆英等[8]根据频散关系对不同频率信号施加不同的相位延时，去除了频散对成像结果的影响。按此思路，可在频域上进行MPDR 算法处理，如此有效解决了频散对MPDR 算法的影响。

针对矩阵求逆计算困难的问题，已有文献提出最小二乘递推算法（Recursive least squares, RLS）来求解矩阵逆[9‑10]，其可与MPDR 算法相结合并进一步优化计算过程，提高效率。而对于奇异矩阵无法求逆的问题，亦有文献提出使用对角加载改进算法，提高算法稳健性[11]。

综上，本文研究了适用于Lamb 波损伤检测的MPDR 算法，其利用自适应算法提高了损伤成像区域的横向分辨率，有效抑制旁瓣伪影；通过在频域上进行波束形成以消除频散对成像结果的影响；通过RLS 算法及对角加载技术相结合以实现谱矩阵的求逆运算，优化了计算过程。

1 MPDR 算法基本原理

1.1 压电阵列接收到的信号模型

用换能器主动激励Lamb 波，使其在铝板中与损伤相互作用发生散射，再由接收压电阵列采集。由于本文考虑在频域上进行MPDR 算法处理以去除频散对成像结果的影响，由此需对接收阵列所采集的频域信号进行建模，根据文献[6]，接收阵元i所接收到的频域信号为

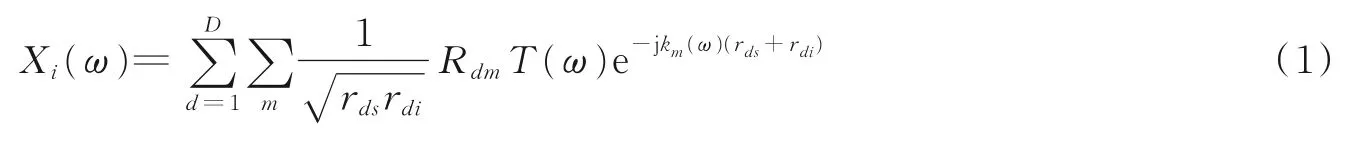
该频域信号由D个空间散射源对应的多模态信号组成，其中D为空间散射点数目；m表示Lamb 波传播模态；rds,rdi分别为信号激励源s到散射点d的距离，散射点d到阵元i的距离，其具体表示为：rds=|zd-zs|，rdi=|zd-zi|，zd、zi、zs分别表示散射点d，阵元i，激励源s的空间位置；T(ω)表示激励信号的频域，Rdm表示散射点d对模态m的Lamb 波的散射系数，km(ω)为模态m，角频率ω所对应的波数，该波数可由文献[12]所研究的Rayleigh‑Lamb 方程求解得出。根据式（1）可推导出M个阵元所接收到频域信号矢量模型为

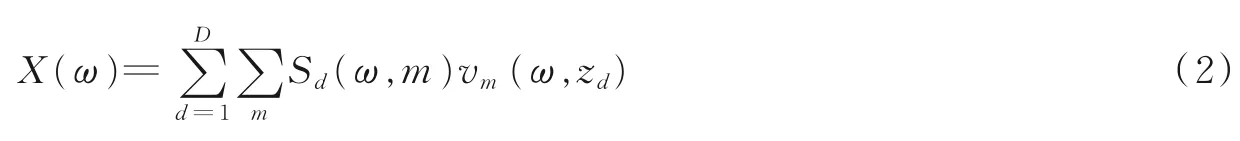
式中

vm(ω,zd)为导向矢量，用于表征阵列接收到单模态、单散射源信号的相位及幅度差异特征，可表示为

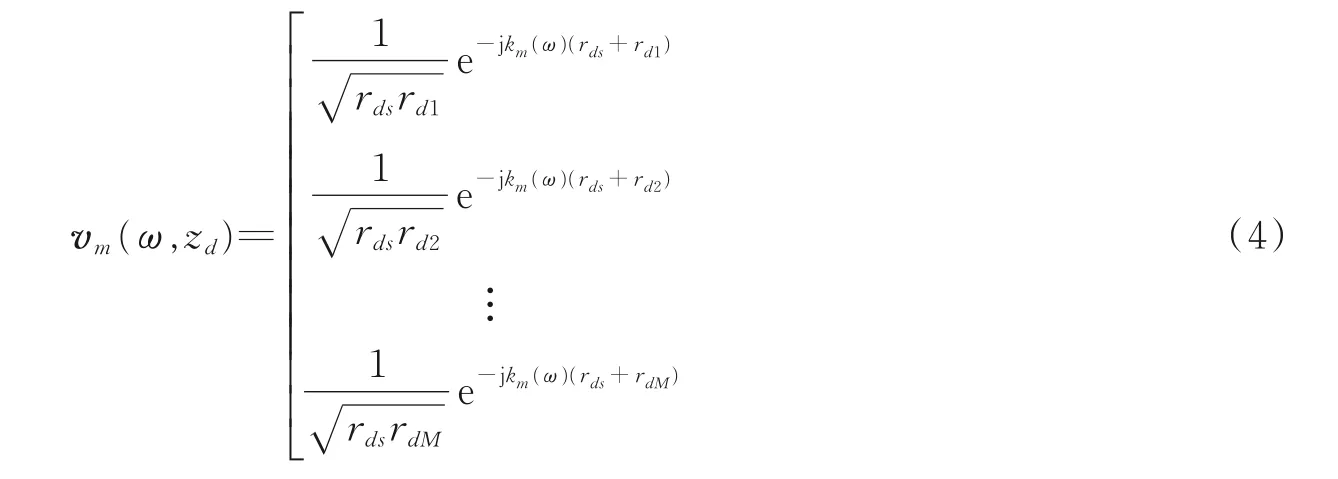
1.2 应用于Lamb 损伤检测的MPDR 权值求解

最小功率波束形式算法的最优加权向量是在保持对空间位置z=(x, y)处传来的Lamb 波增益不变的条件下，使阵列输出的能量最小而得到的[6]。

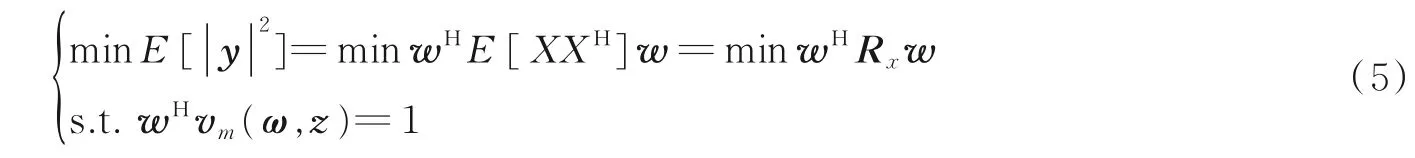
式中Rx为谱矩阵。利用拉格朗日数乘法可解得最优权值矢量为

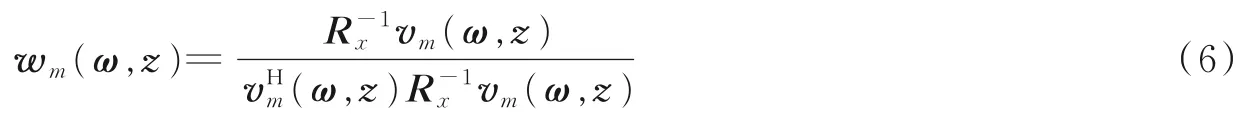
考虑到在单阵元发射、多阵元接收这种检测方案下，接收传感阵列只会接收到一组损伤信号，则对应的X(ω)只有一次采样数据，由此谱矩阵可表示为

本文σ2的取值参考文献[11]选取的方法，则

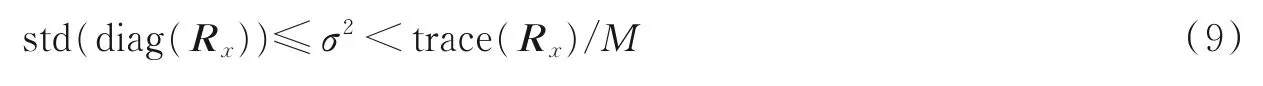
且本文中令

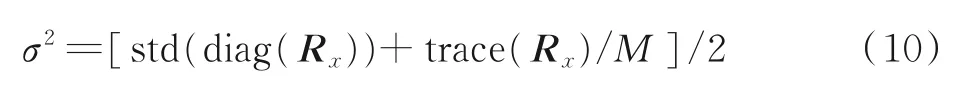
1.3 RLS 递推求逆

在MPDR 最优权值求解中，计算涉及到矩阵求逆运算，常规矩阵求逆采用伴随矩阵求逆法，其耗费极大的计算资源，降低了计算效率。为此本文引入了最小二乘法递推法（Recursion least squares，RLS），其通过迭代形式实现矩阵求逆运算，其具体形式如图1 所示。

X(ω,k)表示对X(ω)的第k次采样，P(k)即为第k次递推得到的谱矩阵逆，而在本文中只需进行一次递推求逆，只需初始化P(0)=I/σ2，递推结果P(1)为所需求解的逆，经递推后的所求矩阵逆为

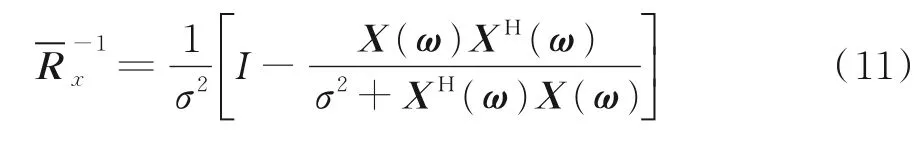
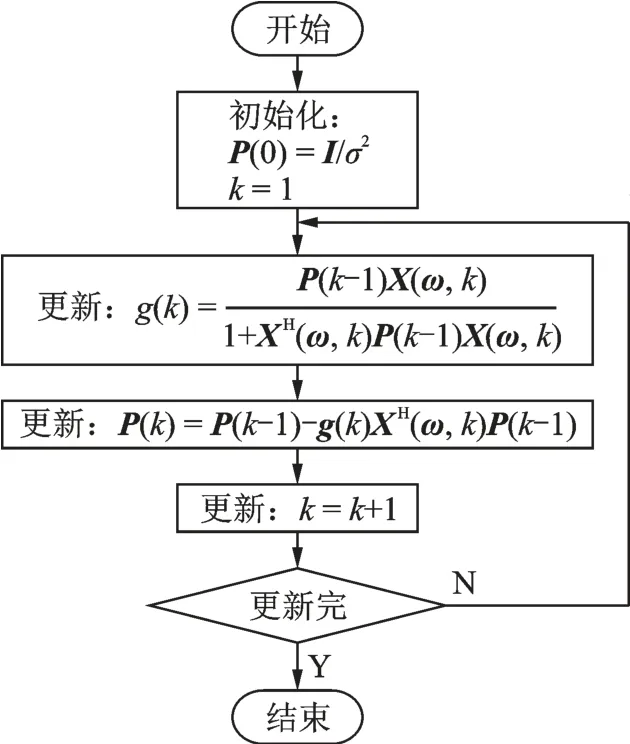
图1 RLS 递推求逆流程图Fig.1 RLS recursive inverse flow chart

而根据式（6），用（a为一复数）代替原并不会使权值wm发生改变，由此可对式（11）进一步简化，令

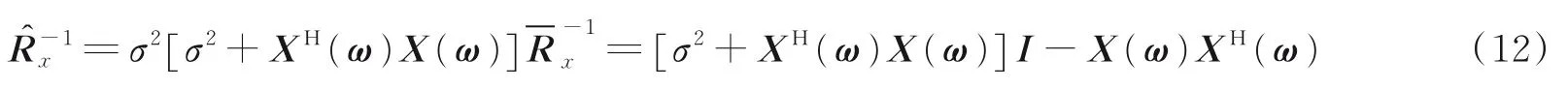
使式（11）中的除法变为乘法，计算更易实现。

1.4 损伤成像指标求解及优化

根据求解的权值，位置z处的波束合成输出

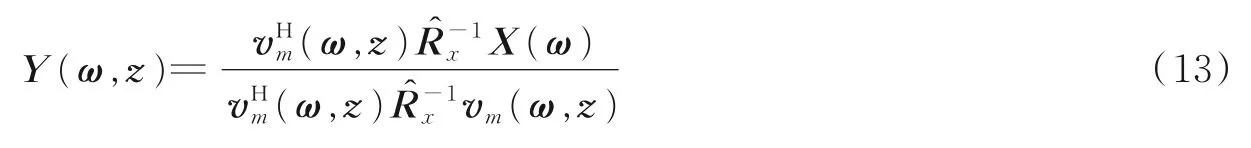
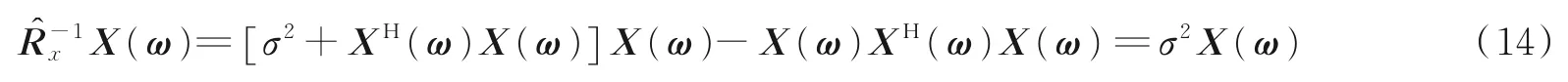
如此式（13）可简化为

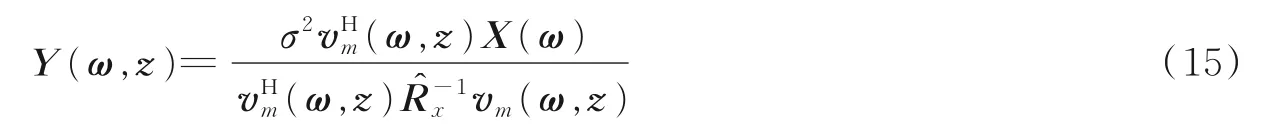
可得式（15）比式（13）少计算M2-1 次复数乘法，M2-M次复数加法（M表示阵元数目）。频域波束合成求解后，即可整合z点所有频域波束合成值Y(ω,z)进行逆傅里叶变换求取z处的成像指标

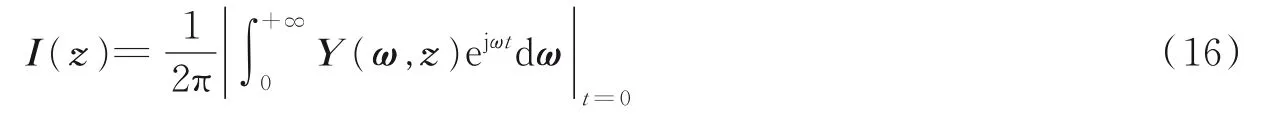
式（16）只对Y(ω,z)的正频率部分进行了逆傅里叶变换，目的是取逆傅里叶变换结果的包络信号，且以零时刻幅值作为z处成像指标输出。

1.5 成像流程

前面的部分详细描述了成像所用到的方法，其具体成像过程如下：

(1)阵列采集Lamb 波信号并从中剔除直达波及边界反射信号得到损伤散射信号。

(2)将信号傅里叶变换到频域，得到频域采样数据X(ω)。

(3)进行谱矩阵求逆运算（如式（12）所示）。

(4)对位置z求取频域波束合成值（如式（15）所示）。

(5)重复步骤(3)、(4)直至所有频率点及位置点的频域波束合成值求解完成。

(6)求取所有位置的成像指标（如式（16）所示）。

2 成像算法的COMSOL 仿真验证

为检验MPDR 算法特性，在Comsol 平台设置如图2（a）所示铝板结构模型，材料参数如表1，激励源位于铝板中心，以150 kHz 中心频率的五峰波作为检测波，采样点间隔为3.86 mm，其为150 kHz 频率下A0模态对应的半波长，取离面方向的结构位移量作为信号输出，最终仿真出的信号如图2（b）所示，其损伤散射信号部分经放大后如图2（c）所示，其中A0模态所引起的主要为离面方向，而S0模态所引起的主要为面内位移[13]，因此离面方向的损伤散射信号以A0模态为主。分别利用MPDR 算法、频域DAS 算法及时域DAS 算法进行成像处理，其最终成像结果如图3 所示。为评估成像结果，引入阵列性能指标（Array performance indicator, API）[14]，该指标定义为损伤处幅值最大值下降到50%之内所有像素点的面积S。

表1 仿真材料相关参数Table 1 Simulation material related parameters

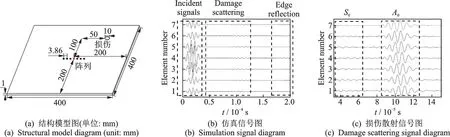
图2 仿真示意图Fig.2 Simulation diagram

图3 仿真成像结果图Fig.3 Simulation imaging results

此处λ取激励信号中心频率下A0模态对应的波长，API 越小，说明成像分辨率越高。对比图3中各个成像结果的API 指数以及损伤位置准确度可得结果如表2 所示，经分析可得如下结果：

（1）MPDR 损伤区域径向分辨率与相较于时域DAS 损伤区域径向分辨率有了显著提高，分析原因在于MPDR 算法能去除频散对成像结果的影响，提高了径向分辨率亦提高了损伤定位准确度。

（2）MPDR 成像结果的损伤区域横向分辨率显著优于时域及频域DAS 算法，且MPDR 算法可有效抑制时域及频域DAS 算法中的旁瓣伪影，分析原因为MPDR 算法可有效抑制非扫查方位的回波信号，保证扫查结果接近真实情况，有效提高了损伤区域的横向分辨率，且抑制了旁瓣伪影。

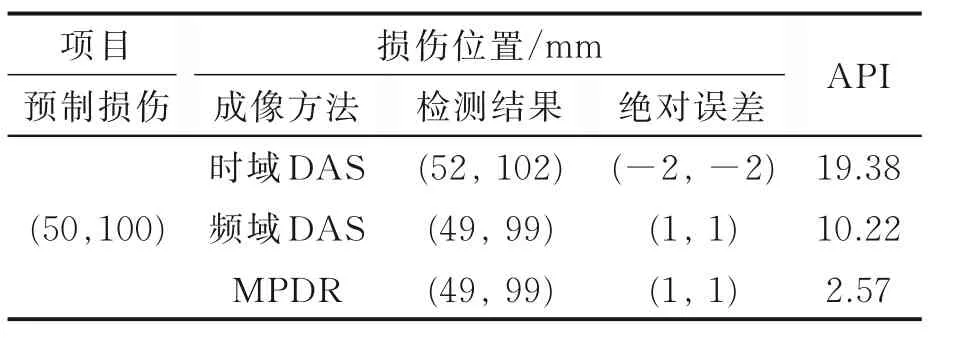
表2 仿真成像结果对比Table 2 Comparison of simulation imaging results

3 实验验证

为进一步验证MPDR 算法的特性，特搭建如图4 所示实验平台。实验中所用的铝板尺寸为1 000 mm×1 000 mm×1 mm，以铝板中心为坐标原点，黏贴7 个间隔为8 mm 的压电片（型号APC851，直径7 mm，厚度0.2 mm）位于(-24 mm, 0 mm)～(24 mm, 0 mm)范围内，预制直径4 mm 圆形通孔损伤位于坐标(50 mm, 100 mm)，压电阵列布置实物如图4（b），具体实验步骤如下：

（1）利用信号发生模块产生100 kHz 五峰波信号，经DA 转换、滤波及高压放大后产生Lamb 波信号，该发射压电片位置位于中心原点。

（2）Lamb 波信号发射之后发射压电片转换为接收功能，接收阵列开始采集信号，阵列将采集到的微弱损伤散射信号经由前端放大、滤波电路、AD 转换传输给FPGA 数据采集系统。

（3）FPGA 数据采集系统将采集到的数据打包通过串口传输至上位机中。

（4）上位机利用Matlab 软件将采集到的信号以A0模态为基准进行成像处理并显示。

最终实验所采集的损伤信号如图5 所示，可以看出损伤散射信号以A0模态为主，而S0模态信号微弱，难以区分，原因在于A0模态导致的结构位移主要在离面方向，而本实验所使用的压电晶片对于离面位移更加敏感，根据此损伤散射信号，最终的损伤成像结果如图6 所示，对比成像结果的API 指数以及损伤位置准确度可得结果见表3。

可得MPDR 算法的成像结果显著优于时域及频域DAS 算法，MPDR 算法的成像有效区域相较于时域DAS算法成像有效区域面积缩小了56.3%；相较于频域DAS 算法的有效区域面积缩小了54.8%。此外MPDR 成像结果有效抑制了旁瓣伪影，有效提高了损伤区域的横向分辨率，此外通过在频域上实施MPDR 算法，有效去除了频散对成像结果的影响，提高了成像结果的径向分辨率。以上结论与仿真结果保持一致，进一步验证了本文所研究MPDR 算法的优异性能。

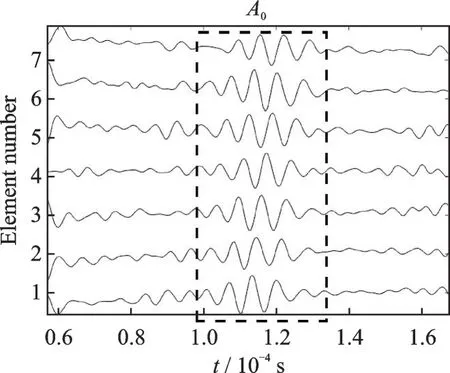
图5 实验损伤散射信号Fig.5 Experimental damage scattering signal

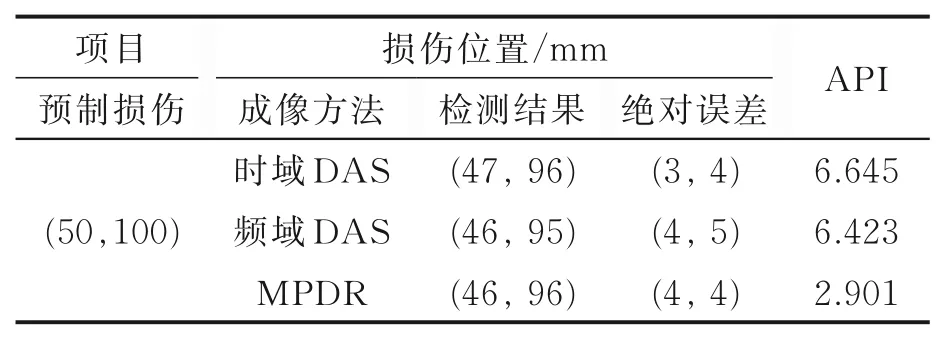
表3 实验结果对比Table 3 Comparison of experimental results

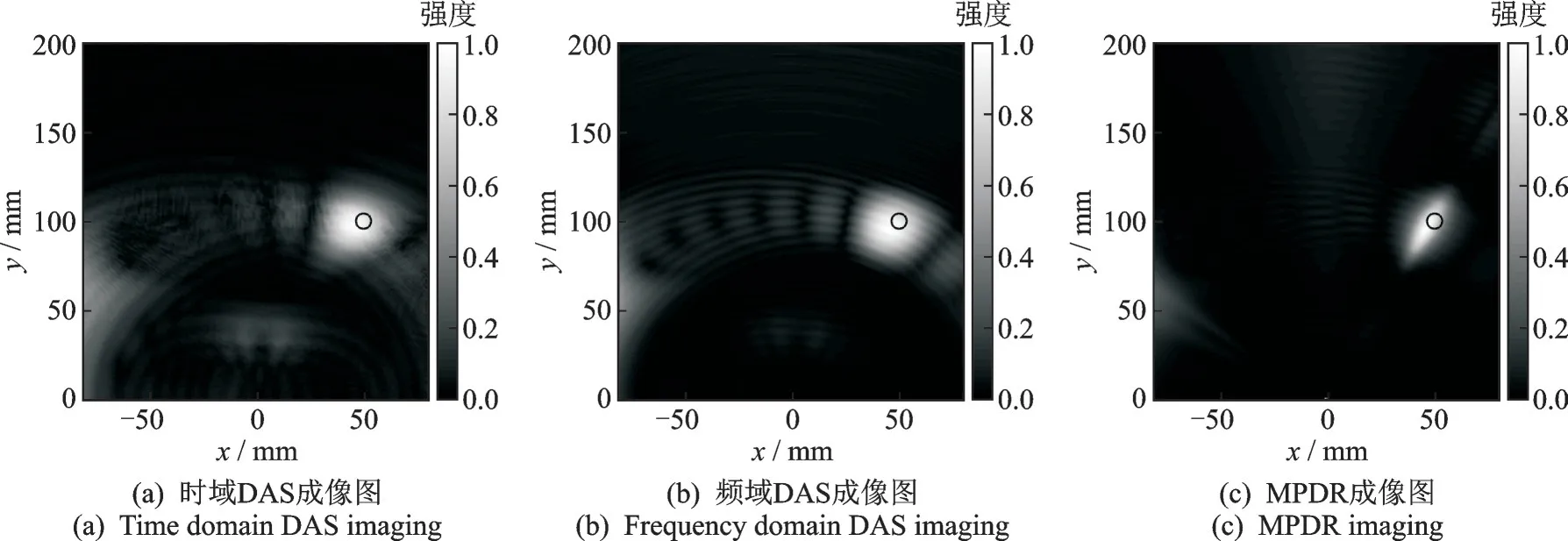
图6 实验成像结果图Fig.6 Experimental imaging results

为分析RLS 递推及算法优化对成像效率的影响，在Matlab 中分别利用优化后的RLS 求逆MPDR 算法以及伴随矩阵求逆MPDR 算法进行成像，其成像过程所耗费时间如表4 所示。对比发现，优化后的RLS 求逆MPDR 算法相较于伴随矩阵求逆MPDR 算法提高了61.4%的计算效率。

表4 成像耗费时间对比Table 4 Comparison of time consuming on imaging

4 结束语

本文提出了一种适用于Lamb 波损伤检测的MPDR 波束形成算法，该算法通过最小二乘递推与对角加载相结合的方式实现了谱矩阵求逆运算，通过变换到频域处理得以消除频散对成像结果的影响。通过仿真与实验表明，与时域DAS 算法相比，本文所研究的MPDR 算法能有效提高成像分辨率，有效抑制旁瓣伪影，去除频散对成像结果的影响，提高最终损伤评估准确度，同时对MPDR 的优化改进使得计算量降低，提高了计算效率。本文所研究的超声Lamb 波相控阵自适应成像方法在金属板状结构的成像检测精度和检测效率方面得到改进，相关成果有望为进一步优化发展自适应波束形成算法提供新方法，也有望为超声Lamb 波相控阵损伤检测的实际工程运用提供理论和方法基础。