基于一致判别相关分析的低分辨率人脸识别算法

张恩豪，陈晓红

（南京航空航天大学理学院，南京，211106）

引 言

近几十年来，人脸识别技术在日常生活中取得了广泛应用。现有的人脸识别系统或算法很多都是面对高分辨率(High resolution, HR)或超分辨率（super resolution，SR）的人脸图像，而在现实生活中，常需要对低分辨率（Low resolution，LR）人脸图像进行识别[1]。例如：为了社会安全保障和执法目的，很多公共区域安装监控系统，由于相机与被摄对象之间的距离较大，所捕获图像中的人脸区域通常较小，导致所捕捉的图像是LR 人脸图像。与HR 图像相比，LR 图像分辨率比较低，包含更多的噪声，且所含有的判别信息较少，这在很大程度上影响了传统人脸识别技术的性能，因而对LR 人脸图像的识别成为一种挑战[2]。

为解决LR 人脸图像的识别问题，研究者们针对LR 人脸图像相继提出众多算法。早期的算法中，主要采用基于超分辨率(Super resolution，SR)的方法[3⁃5]，将LR 图像重建得到对应的SR 图像，然后在超分辨率空间中基于SR 图像进行识别，也被称为“两步走”。如：Gunturk 等[6]在低维人脸空间中直接构造识别信息，从而实现SR 图像的重组，大大降低了重建超分辨率图像的计算复杂度；Freeman 等[7]提出VISTA⁃Vision 算法，通过使用逐对马尔科夫链进行SR 图像重组；Dong 等[8]基于字典学习的方法，在LR 和HR 特征空间中通过字典学习得到稀疏编码系数来生成SR 人脸图像；Kim 等[9]基于回归的方法首先学习从LR 特征空间到SR 特征空间的映射函数，然后利用学得的映射函数重新构造SR 人脸图像。“两步走”算法虽然提高了LR 人脸图像的识别率，但是这些算法的识别对象主要是SR 图像，忽略了LR本身的特征信息，并且重建SR 图像会提高算法的时间复杂度。

针对“两步走”算法的缺点，Li 等[10]提出了一种无需构建SR 图像的LR 人脸图像识别新方法，基于联合映射(Coupled mapping，CM)，将LR 和HR 人脸图像投影到一致的特征空间中，通过优化目标函数来学习CMs；然后基于投影后的训练样本，采用K 近邻（K⁃nearest neighbor，KNN）分类器进行分类。Huang 等[11]提出一种基于典型相关分析(Canonical correlation analysis，CCA)[12]的超分辨率人脸识别方法，将HR 和LR 人脸图像的线性相关性最大化，然后将LR 和HR 图像特征投影到一致特征空间中。基于CCA 的超分辨率算法比“两步走”算法获得更高的识别结果，但是CCA 本质上是一种线性学习方法，不能获得LR 图像和HR 图像的非线性关系。Zhang 等[13]在此基础上，利用核CCA(Kernel canonical cor⁃relation analysis，KCCA)[14]学得 LR 和 HR 图像的非线性关系，由径向基函数(Radial basis function，RBF)建立LR 和HR 图像间的非线性投影，进一步提高了LR 图像的识别能力。

综上可知，以上算法大都属于无监督学习，学习过程忽略了数据所包含的类标号信息，为提取更有利于分类的特征，并克服Huang 和Zhang 等所提出算法的局限性，本文考虑将数据的监督信息引入到LR 人脸识别算法中，可提取HR 和LR 人脸图像的有利于分类的低维特征，实验表明该方法对于LR 人脸图像的识别效果有所提升。进一步，从多视图学习的角度分析，不同的视图具有相同的源域，所以不同的视图间存在潜在的视图一致性，而这正是多视图学习取得成功的基石[15⁃16]。本文提出一致判别相关分析(Consistent discriminant correlation analysis，CDCA)。CDCA 算法同时考虑数据的监督信息和视图间的一致性信息，使得所提取的不同视图的低维特征存在较好一致性。进一步将CDCA 算法融入低分辨率人脸识别框架中，利用CDCA 算法提取LR 和HR 人脸图像的低维特征，之后利用径向基函数和最近邻算法实现低分辨率的人脸识别。实验表明，相比于其他算法，该算法有较好的识别结果和鲁棒性，而且随着所提取的低维特征的维数和分辨率的不同，该算法有更好的稳定性。

1 多视图降维算法

1.1 典型相关分析

CCA 是一种用于建模两个变量集之间关系的技术，能够识别并量化两组变量之间的关联程度，旨在 最 大 化 两 个 数 据 集 的 低 维 映 射 之 间 的 相 关 性[12]。 给 定 随 机 变 量X1=分别表示X1和X2样本集第i类的第j个样本，ni表示第i类的样本数目。CCA 旨在寻找一组投影矩阵的相关性最大。不失一般性，假设两个视图的样本均已中心化，则CCA 的目标函数定义为

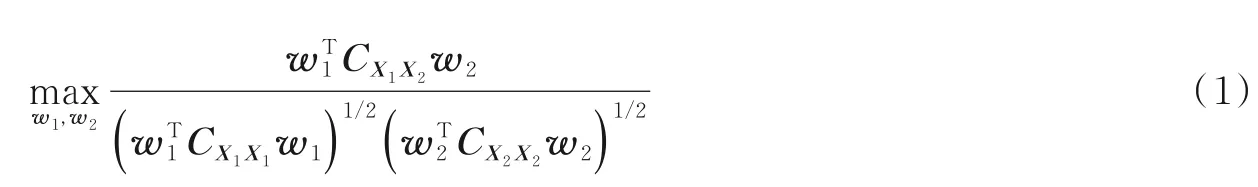
CCA 是从两视图数据中提取信息的技术，仅适用于线性空间中，而文献[14]则把核技巧融入CCA得到KCCA。Huang 和Zhang 分别将CCA 和KCCA 算法应用到低分辨率人脸识别中，得到了较好的识别效果。

1.2 一致判别典型相关分析

1.2.1 判别信息

在分类学习中，各样本的判别信息非常重要，CCA 和KCCA 的无监督特性限制了降维后的可分离性。针对该问题，孙廷凯等[17]在典型相关分析中融入数据的判别信息，得到如下目标函数

基于尺度不变性，可转化为

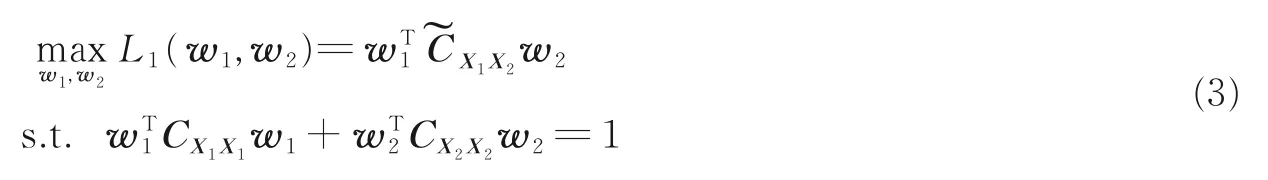
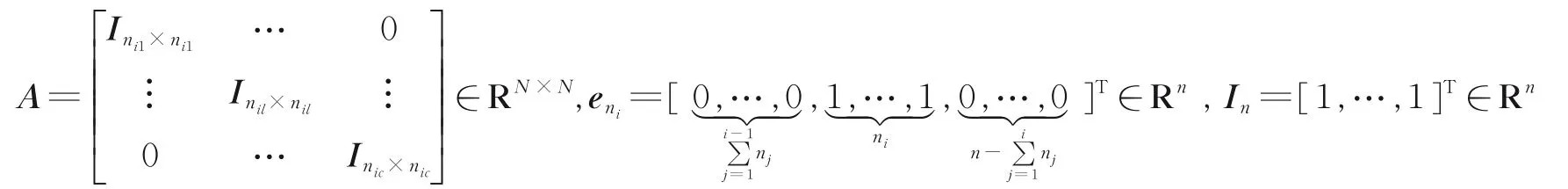
式中Cw和Cb分别定义为

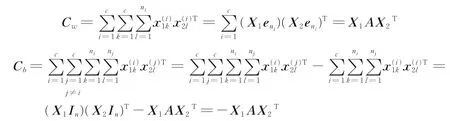
因为样本已经中心化，则有X1In=0,X2In=0，则式(3)可转化为

由拉格朗日乘子法易得投影矩阵w1,w2。

1.2.2 视图一致性信息

因为多视图数据大都是由同一个目标生成的，所以各个视图间应该存在着一定的对应关系。例如:HR 人脸图像和LR 人脸图像均来自于同一个人，分别将其定义为X1和X2，则X1和X2存在着某种转换关系，即存在矩阵R，使得

文献[16]已证明，投影矩阵w1,w2同样存在转换关系

且第i个视图的投影矩阵wi可以写为等价形式

式中βi(i=1,2)表示投影矩阵wi(i=1,2)的特征结构,由式(4—6)可得

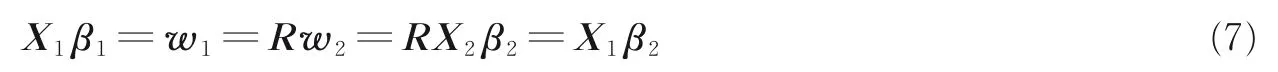
从而有β1=β2，即对于不同的视图，每个投影矩阵wi(i=1,2)所提取的特征结构βi相同。不失一般性，可以认为对应于同一目标的多视图数据有相似的特征结构，即不同视图的投影矩阵是相关的，这可称为视图一致性[15]，从而得到描述视图一致性的函数，有

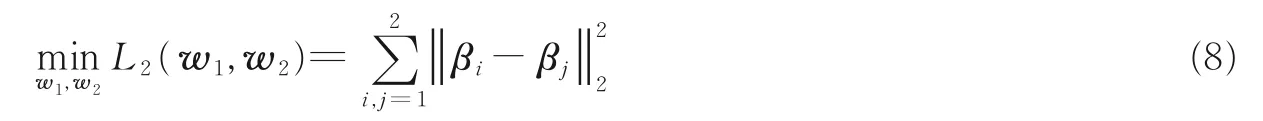
1.2.3 判别信息与一致性信息结合

结合1.2.1 节和1.2.2 节的分析，同时考虑数据的类信息和视图间的一致性，得到一致性判别相关分析。具体而言，就是在目标函数L1中引入一致性信息，结合L2得到CDCA 目标函数

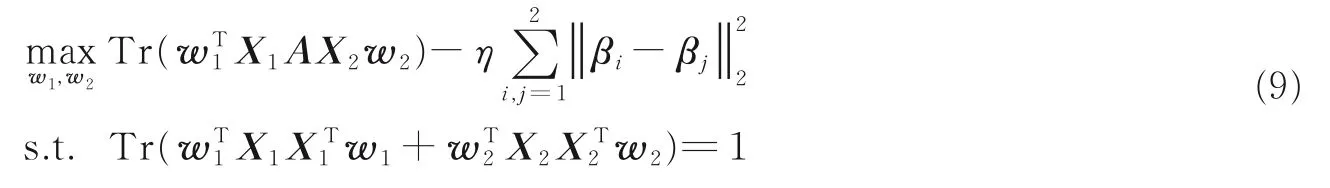
η为平衡系数，式(6)可转化为

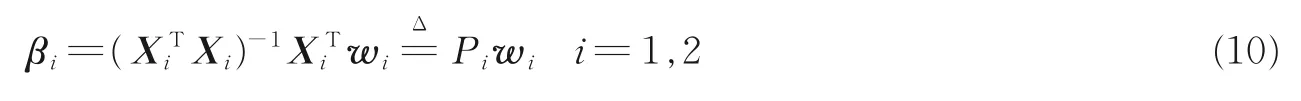
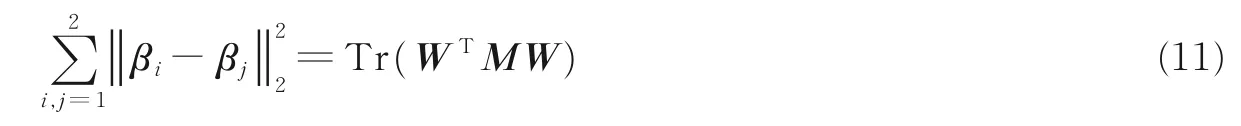
式中

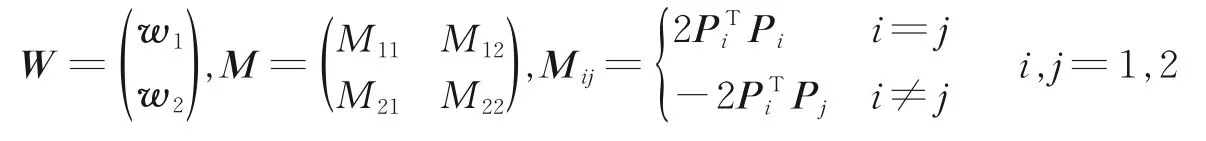
将式(11)代入式(9)，CDCA 目标函数可表示为

式中

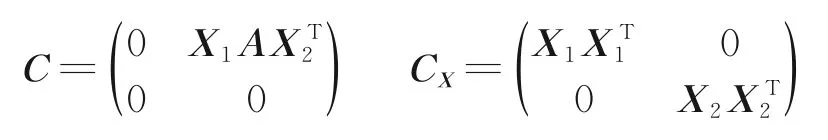
由拉格朗日乘子法，可得

2 算法描述

本节中给出算法的详细过程。首先提取HR 和LR 人脸图像的主成分特征，然后利用CDCA 学习HR 与LR 面部特征以提取监督信息，再利用RBF 模型构建相关特征之间的非线性映射，最后由KNN分类器进行识别（图1）。

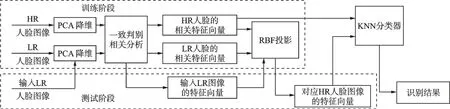
图1 算法流程图Fig.1 Flowchart of algorithm

2.1 用PCA 提取特征

假设给定HR 和LR 人脸图像是来自c个类的n对训练样本定义为每类的样本总数为各个视图样本总数。对于人脸识别而言，通常训练样本的维数很高，导致巨大的计算成本。为降低时间复杂度，首先利用主成分分析(Principal component analysis，PCA)[18]对样本进行降维。记

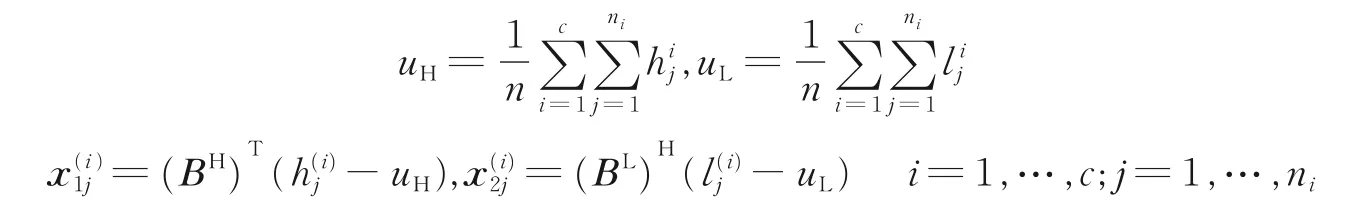
式中：BH和BL分别表示由PCA 得到的特征提取矩阵，uH和uL分别表示HR 和LR 人脸图像训练集的均值表示经过PCA 降维后得到的特征向量。记为

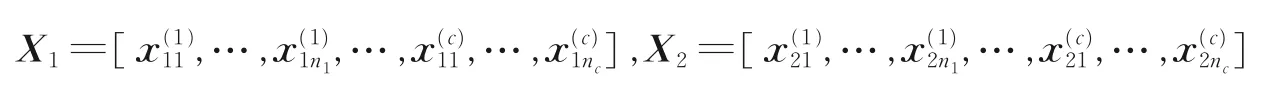
2.2 利用CDCA 计算相关特性

为分别探究融入监督信息和一致性信息对识别结果的影响，本文也研究了只融入监督信息对识别结果的影响。首先研究监督信息对识别结果的影响。对得到的新特征矩阵X1和X2(假设X1和X2已零均值化)，由目标函数L1计算相关特性，得到如下优化问题

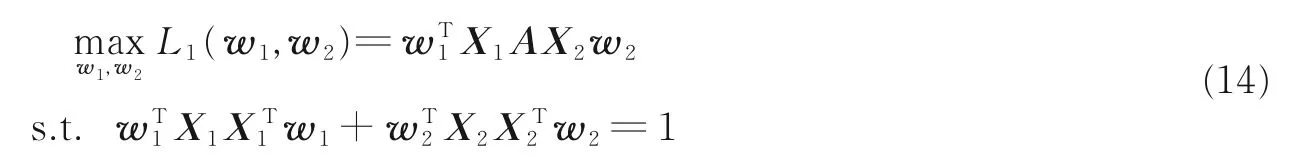
通过拉格朗日乘子法转化为广义特征值问题，可得到投影矩阵w1和w2。其次研究监督信息和一致性信息对识别结果的共同影响。由CDCA 算法计算相关特性，由式(12)可得

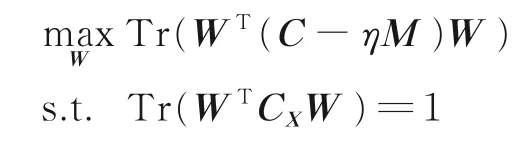
式中

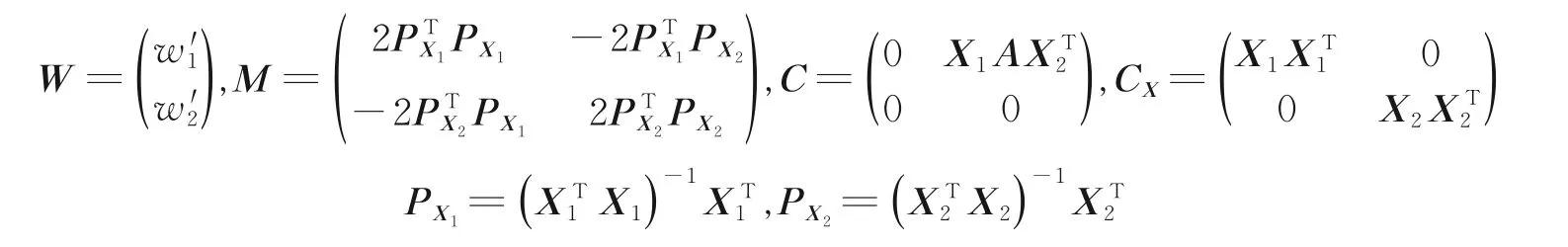
同样可由拉格朗日乘子法得到投影矩阵W。

2.3 LR 和HR 人脸相关特征的非线性映射

在学习训练集HR 与LR 的相关特间的非线性映射关系时，这个问题可以转化为寻找一个近似函数，建立HR 与LR 人脸图像的相关特征之间的映射。RBF 通常用于构建这类函数的近似。径向函数是一种取值只依赖于样本到与原点(或其他中心点)的距离的函数，即φ(x) =φ(‖x‖)，‖ · ‖通常指欧式距离。RBF 就是用一组径向函数的加权和来实现某种函数逼近[19⁃20]。根据Huang 的方法[11]，利用以下映射建立LR 与HR 人脸图像相关特征之间的关系

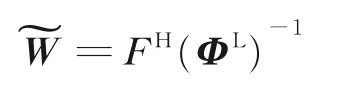
在实验中，如果ΦL不可逆，取ΦL=ΦL+τI，I为单位矩阵，τ为较小的正值，如τ=10-3。由投影矩阵可以得到给定LR 人脸图像所对应的HR 人脸特征图像，从而实现LR 人脸图像的识别。

3 实验结果与分析

为了验证所提出方法的有效性，分别在ORL、Multi⁃PIE 和Yale 人脸数据集上进行实验对比。本文选取了直接使用原始HR 人脸图像进行识别(HR⁃PCA)，使用LR 人脸图像进行识别(LR⁃PCA)、Wang 的方法(PCA⁃RBF)[5]，Huang 的方法(Huang’s method)[11]以及 Zhang 的方法(Zhang’s method)[13]进行了比较。在实验中，Method(1)是只使用监督信息进行的特征提取，而Method(2)是使用CDCA 算法进行的特征提取，加粗字体表示每组实验的最优结果，括号里的数表示循环30 次识别率的方差(方差不足0.01%的记为0.01%)。

3.1 ORL 人脸数据集实验

ORL 人脸数据集，又称AT&T 人脸数据集，包含40 个的不同受试者，其中每人有10 幅不同的图像，图像是在不同的时间、不同的照明、面部表情(开/闭着眼睛，微笑/不笑)和面部的细节(眼镜/不带眼镜)分别拍摄的，图像为均匀黑色背景的正面人脸(允许有小角度偏离)。实验中，每次随机选取每个个体5 个不同的视角作为训练集，剩余的不同视角作为测试集，选择的HR 图像为32像素×32 像素，LR 图像为8像素×8 像素，如图2 所示。在Zhang’s 的方法中，设置核参数为0.9，径向基函数中的参数设置为2；在使用CDCA 算法提取特征时，设置参数η=0.8。表1 列出ORL 人脸数据集上各算法在不同特征维数下的识别率。

图2 HR/LR 图像集IFig.2 HR/LR face image I

表1 各算法在ORL 数据集上不同特征维数的识别率Table 1 Recognition rate of different feature dimensions in ORL database %

通过表1 的实验结果不难发现，当选取的特征维数是40 维时，Method(2)的识别率为90.25%，超过直接使用原始HR 图像进行实验的识别率89.95%，并且Method(1)和Method(2)的识别率显著高于其他算法；特征维数为50 维时，Method(1)和Method(2)的识别率分别是91.60%和93.74%，Method(2)的识别率略高于直接使用原始HR 图像进行实验的识别率91.90%；当选取特征为数位60 维时，Method(1)和Method(2)的识别率分别为97.20%和95.55% 均高于其他算法的识别率。尽管在60 维时，Method(2)的识别率仅有95.55%，但是对于不同的特征维数，Method(2)算法变化幅度不大，说明Method(2)算法相比于其他算法更稳定，鲁棒性更好。综上说明提取特征时融入类信息，可提取更有利于分类的低维特征，并且视图一致性信息的融入能够提高算法的鲁棒性。

3.2 Multi⁃PIE 人脸数据集实验

Multi⁃PIE (Pose illumination and expression) 数据集被用来评估面部识别的姿态，它包含了75 万张不同视图下的337 个人的人脸图片。研究对象在15 个视角和19 个光照条件下拍摄了一系列面部表情，此外还获得了高分辨率的正面图像。在实验中，选取30 个的不同受试者，其中选取每人的10 幅不同的图像，共300 张灰度图像进行实验，每次随机选取每个个体的5 张人脸作为训练集，剩余图像作为测试集，选择的 HR 图像为 32像素 × 32 像素，LR 图像为 11像素 × 11 像素。表2 列出各算法在 Multi⁃PIE 人脸数据集对于不同PCA 特征维数（30 维，40 维和50 维）下的实验结果。同3.1 节的实验结果相似，Meth⁃od(2)算法在特征维数较低时，有较好的识别结果，当选取的PCA 特征维数较高时，Method(1)算法有较好的识别结果。说明当特征维数较低，判别信息和视图一致性的融入，能够显著提高识别结果。尽管当特征维数为50 维时，Method(2)的识别率仅有93.67%，但是可以看出Method(2)算法随着特征维数的增加，变化比较稳定，并且在低维情况下相比于其他算法有更好的识别结果，说明在低维情况下，CDCA算法能更充分利用数据本身的特征信息。

表2 各算法在Multi⁃PIE 数据集上不同特征维数的识别率Table 2 Recognition rate of different feature dimensions in Multi⁃PIE database %

3.3 在Yale 人脸数据集进行识别

Yale 人脸数据集包含15 个的不同受试者，其中每人有11 幅不同的图像，共165 张灰度图像，图像是在不同的面部表情和环境下拍摄的。实验中，每次仅随机选取每个个体的5 张人脸作为训练集，另外任选5 张人脸作为测试集，该实验中选择的HR 图像为32像素×32 像素，LR 图像的分辨率分别为9像素×9像素、10像素×10像素、11像素×11像素。实验目的是研究不同分辨率的LR 人脸图像对各算法识别率的影响，图3 列出了实验需要的部分HR 和LR 人脸图像。实验中，在Zhang’s 的方法中，设置核参数为1.06，径向基函数中的参数设置为2，CDCA 算法参数设置为0.01。表3 列出在Yale 人脸数据集上各算法在不同分辨率下的识别率。由表3 容易发现，当选取的分辨率是9 像素×9 像素时，Meth⁃od(1)的识别率为95.89%，显著高于其他算法的识别率；分辨率为10 像素×10 像素时，Method(1)和Method(2)的识别率分别为98.93%和97.91%，显著高于其他算法的识别率；当选取分辨率为11像素×11像素时，Method(2)的识别率达到99.64%均高于其他算法的识别率。容易发现，当所选取的人脸图像分辨率相同时，Method(1)和Method(2)的识别率优于其他算法。

图3 HR/LR 图像集IIFig.3 HR/LR face image II

表3 各算法在Yale 数据集上不同分辨率下的识别率Table 3 Recognition rate of each algorithm at different resolutions on Yale database %

3.4 CDCA 算法参数的分析

在优化求解CDCA 算法时，参数η可能会影响实验效果，所以该实验主要考察参数η对实验结果的影响。实验中，通过对Multi⁃PIE 和Yale 数据集上Method(2)算法设置不同的参数η值，观察识别率的变化情况。表4 和表5 分别是在Multi⁃PIE 和Yale 数据集上，不同参数对识别率的影响情况。实验中选取的HR 图像为32像素×32 像素，LR 图像为11像素×11 像素，所提取的PCA 特征维数是90 维。

表4 Multi⁃PIE 数据集上不同参数对识别率的影响Table 4 Effect of different parameters on the Multi⁃PIE database

表5 Yale 数据集上不同参数对识别率的影响Table 5 Effect of different parameters on the Yale database

由表4 和表5 可以得到，识别率随着参数值的增大呈递增的趋势。在Multi⁃PIE 和Yale 数据集上，当参数值分别为0.2 和3.0 时，识别率达到最大，之后识别率随着参数值的增大趋于稳定。容易发现，识别率的变化随着参数的改变波动不大，说明该算法比较稳定，鲁棒性较好。图4 给出了在Multi⁃PIE 和Yale 人脸数据集上，Method(2)算法的识别率随着参数值变化趋势图。

图4 识别率随参数值变化趋势图Fig.4 Trend chart of recognition rate with parameter value

本节通过实验分析，验证本文所提出算法的优越性。在3.1 节和3.2 节中，分别在ORL 和Multi⁃PIE人脸数据集上进行实验，目的是为探究当提取的LR 人脸图像的特征维数不相同时，对实验结果的影响。实验表明本文所提出的算法在不同特征维数下均有较好的识别率；在3.3 节中，通过在Yale 人脸数据集上实验，研究了各算法在不同分辨率的LR 人脸图像的识别效果，实验表明本文提出的算法在不同分辨率的LR 人脸图像上有较好的识别结果；在3.4 节中，通过对Multi⁃PIE 和Yale 数据集上设置不同的参数值，观察Method(2)算法对LR 人脸图像识别率的变化情况，实验表明识别率的变化随着参数的改变波动不大，说明该算法比较稳定，鲁棒性较好。

4 结束语

本文在CCA 的基础上，同时考虑数据的判别信息和视图间的一致性，提出CDCA 算法；并针对LR人脸图像识别率较低的问题，提出基于CDCA 的低分辨率人脸识别算法。在LR 人脸识别算法中，利用CDCA 获取HR 与LR 人脸图像整体特征之间的相关子空间，之后利用RBF 和KNN 分类器进行人脸识别。本文所提出的算法不仅利用数据的标签信息，而且考虑了视图间一致性信息。实验表明，与其他低分辨率人脸识别算法相比，本文提出的方法在不同的数据集下有较高的识别率和更好的鲁棒性。CDCA 是从双视图数据中提取特征的算法，仅适用于线性空间中；在非线性情况下可以参考文献[21⁃23]中的方法，将该算法拓展到非线性空间中，从而可以提取HR 与LR 人脸图像特征之间的非线性关系，进一步提高识别率；针对CDCA 仅适用于双视图数据的问题，可以利用文献[24⁃26]的方法将CDCA算法推广到多个视图。