基于迭代的多频频率估计方法

陈 皓，雷 艺

（1.中国电子科技集团第三十八研究所孔径阵列与空间探测安徽省重点实验室，合肥，230031；2.合肥工业大学计算机与信息学院，合肥，230009）

引 言

调频连续波（Frequency modulated continuous wave，FMCW）雷达是一种常用的雷达，在军民产业中均有广泛的使用。FMCW 雷达发射连续调频信号，利用发送和接收的频率之差计算目标的距离。因此，雷达需要对发送与接收信号的差频信号进行频率估计，频率估计的精度直接影响雷达测距的精度。频率估计中最简单有效的方法是利用离散傅里叶变换（Discrete Fourier transform，DFT）把信号从时域变换到频域，在频域可以直接得到信号的频率值。但是利用DFT 进行频率估计容易带来一些测量误差。误差主要来源于两方面：（1）离散变换的栅栏效应，DFT 的结果是频谱的采样值，难以保证频谱峰值正好和待测频率值重合；（2）负频谱泄漏，实数信号的频谱既包含正频谱也包含负频谱，正负频谱叠加后的总频谱最大值与信号的真实频率会出现偏差。

为了解决栅栏效应带来的误差，该领域研究者们已提出很多有效的算法［1‑4］，其中Candon 算法［5］和Orguner 算法［6］是复指数信号频率估计中最经典的算法，只需利用DFT 结果的3 个采样点即可计算出精确的频率值。但由于没有考虑负频谱干扰，这两种方法在实数信号的频率估计中并不适用。为了抑制负频谱干扰，学者们又提出了加窗算法，其中包括一些常用的加窗算法［7］（如Hamming，Hann 和Blackman 窗）以及基于最大旁瓣衰减（Maximum‑sidelobe‑decay，MSD）窗的高精度算法。使用MSD 窗的算法有经典三点法［8］，以及在经典三点法基础上改进而来的新三点法［9］。相比经典三点法，改进三点法增加了纠正因子，能够比经典三点法有更好的负频谱抑制效果。同时，Borkowski 等基于MSD 窗提出的算法［10］也能够达到非常高的频率估计精度。实际应用中，FMCW 雷达测距时往往不止探测一个目标，当对多个频率同时进行频率估计时，除了单频估计遇到的栅栏效应和负频谱干扰以外，多个频率频谱之间的互相干扰也严重影响频率估计的精度。加窗方法虽然也能对多个频率之间的互相干扰有一定抑制，但无论在频率估计精度还是计算复杂度上都有一定的局限性。本文首先对多频信号的离散频域形式进行了详细推导，得到每个频率对应的最大谱线和其左右两谱线的数学表达式。进而定义了干扰系数，并采取迭代的手段，利用两种不同的方法逐步消除负频谱和其他频率带来的干扰。仿真实验证明，本文提出方法相比传统加窗算法在频率估计精度上有明显提升，而且由于不需要进行加窗处理，也降低了计算复杂度。

1 多频频率估计基础理论

假设采集的信号中有M个频率分量（f1，f2，…，fM），高斯白噪声下的多频离散时间信号表示为

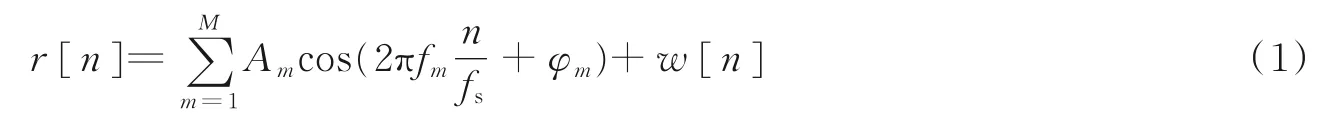
式中：fm为信号的频率；fs为采样频率；Am为第m个频率信号的幅度；φm为第m个频率信号的初始相位。式（1）也可以表示成复数信号相加的形式

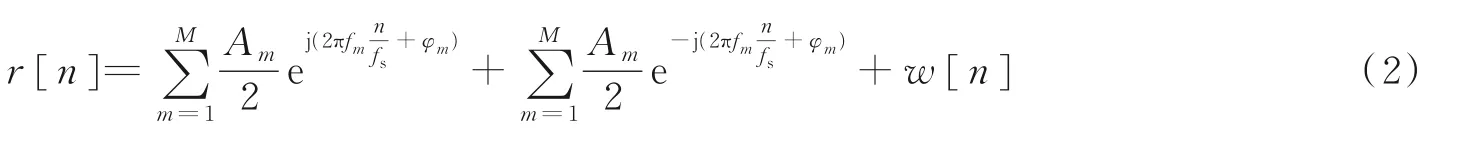
进而对式（2）进行N点DFT 可以得到信号的离散频域表示为

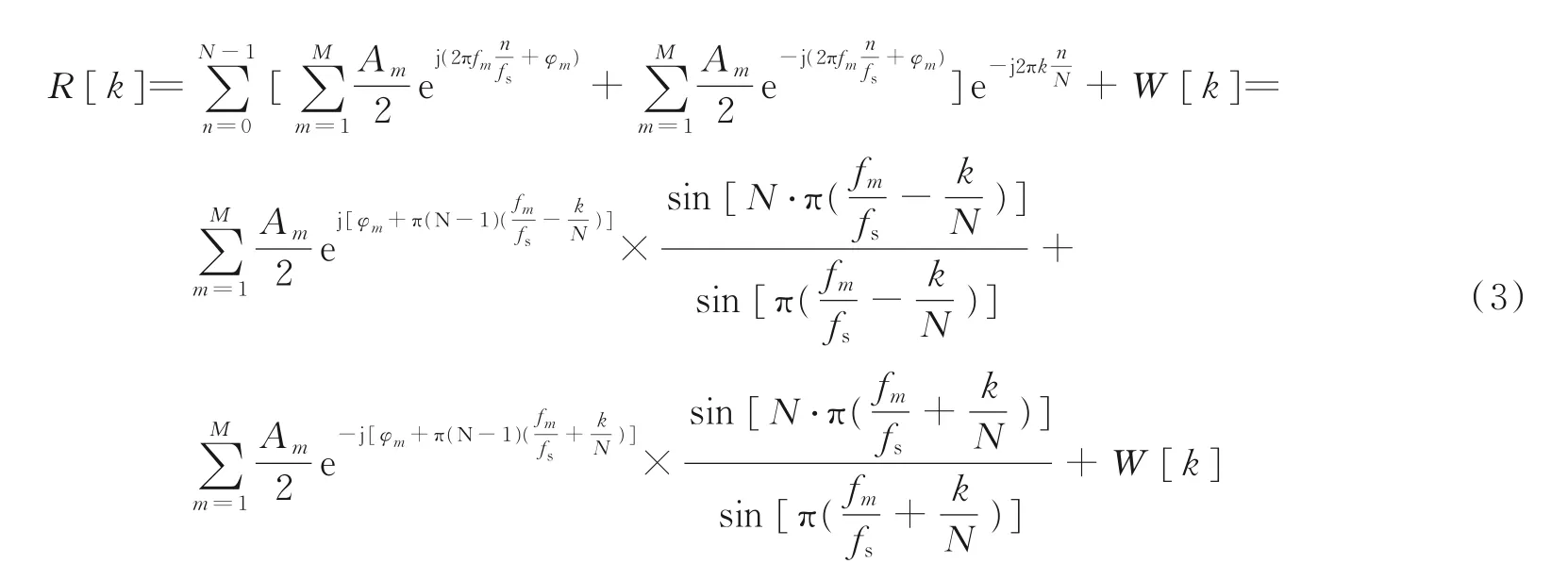
本文通过DFT 结果中每个频率附近的3 个采样点对多个频率值进行估计。待测频率fm可以表示为fm=fs⋅(km+δm)/N，其中km为整数部分，δm(-0.5 ≤δm<0.5)为分数部分。km可以从 DFT 的结果直接得到，精确频率估计的目的即为估计δm的值。首先在DFT 结果中的前N/2 个点里寻找第m个频率对应的最大谱线和其左右两谱线。其对应的数学表达式为

为了后续的推导方便，本文把R[km]、R[km-1]、R[km+1]表示成理想的无干扰项和干扰项的相加（干扰项包括负频谱干扰和其他频率带来的干扰），于是本文定义R[km]、R[km-1]、R[km+1]所对应的理想谱线值为am、bm、cm（即为无负频谱干扰和其他频率频谱干扰时的理想谱线值），并定义：

频率i对频率m最大谱线的干扰系数为

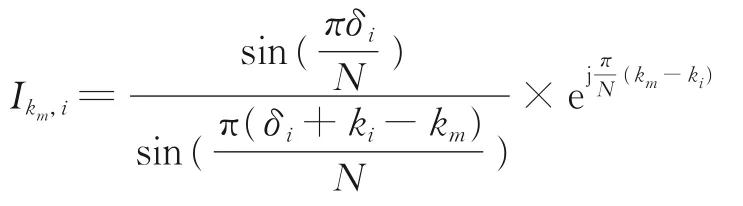
频率i对频率m最大谱线左侧谱线的干扰系数为

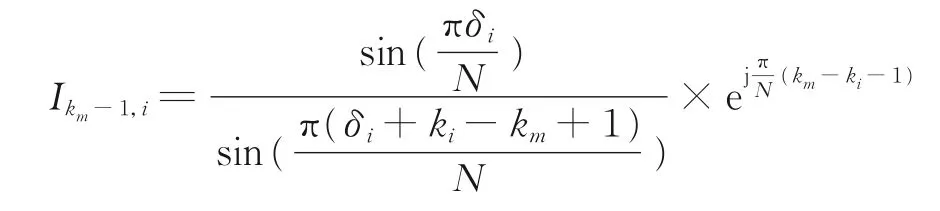
频率i对频率m最大谱线右侧谱线的干扰系数为

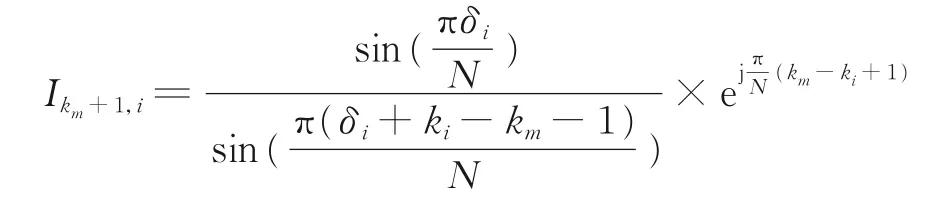
频率i的负频谱对频率m最大谱线的干扰系数为

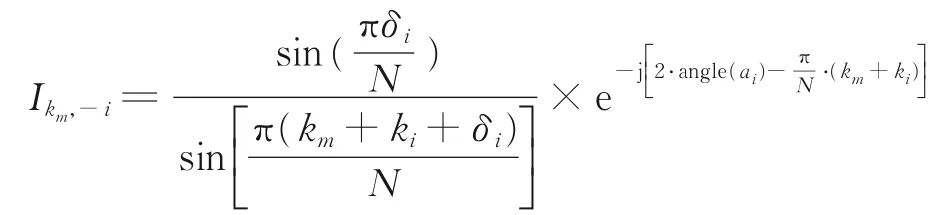
频率i的负频谱对频率m最大谱线左侧谱线的干扰系数为

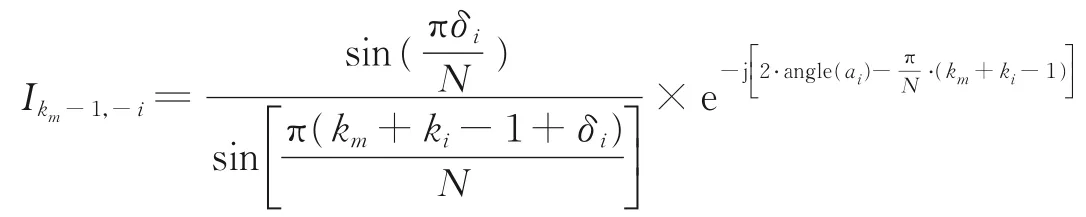
频率i的负频谱对频率m最大谱线右侧谱线的干扰系数为

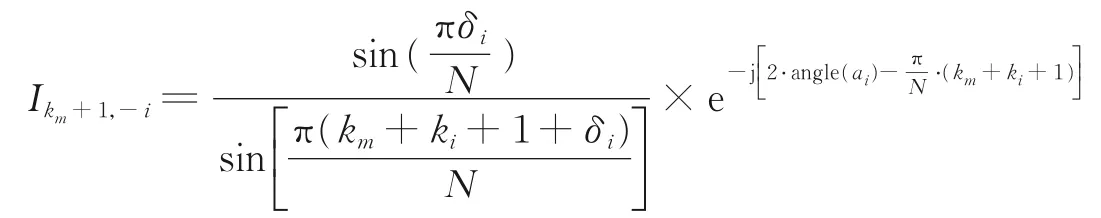
定义了上述参量以后，式（4—6）即可表示为

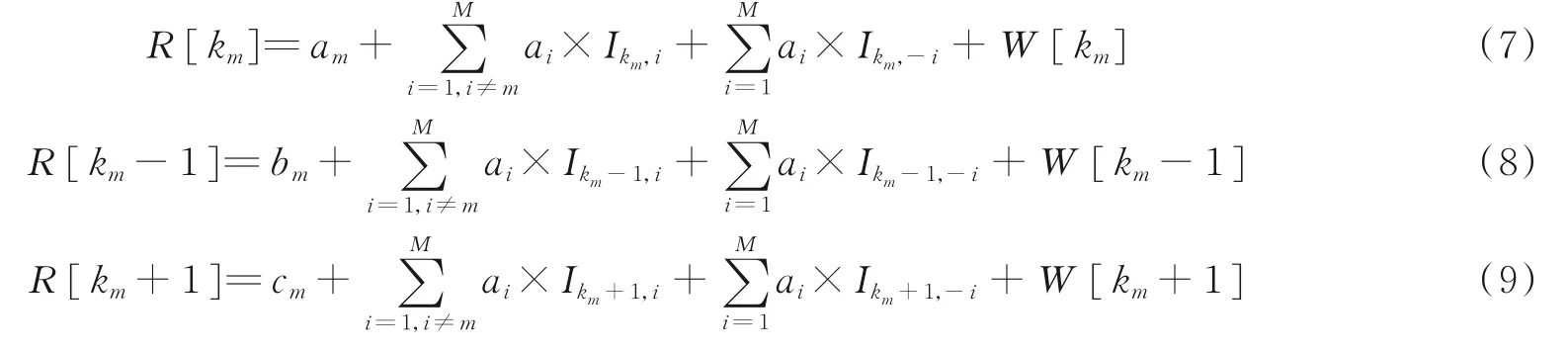
2 基于迭代的多频频率估计算法

本文目的是根据已知的R[km]、R[km-1]、R[km+1]求得am、bm、cm，进而利用 Orguner 算法进行精确的频率估计。Orguner 算法在无噪声无负频率干扰时对单频信号进行无偏估计，是对复指数信号进行频率估计的最佳算法之一，其计算公式为［6］

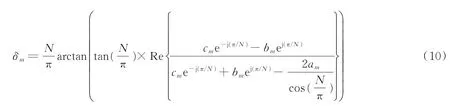
由式（7—9）可以看出，干扰系数是与频率估计结果相关的值，方程没有解析解。因此，为了得到am、bm、cm的值，本文提出了迭代的方法。通过数次迭代得到am、bm、cm的近似值后，再利用 Orguner 算法进行精确的频率估计。

迭代法在一些单频频率估计方法中也有应用［11‑13］。在这些方法中，迭代目的都是为了尽可能多地去除负频谱带来的干扰，因为负频谱的干扰越小，频率估计就越精确。但是这些方法都只关心单频情形下负频谱的干扰，对于多频情形并没有考虑，而实际FMCW 雷达应用中，多目标即多频的情况更为普遍，而频率之间的干扰也比负频谱的干扰更大。因此本文迭代的思路为：首先假设没有负频谱和其他频率的干扰，得到初步的频率估计值，进而根据初步的频率估计值计算出负频率和其他频率的干扰值并进行剔除，从而得到更精确的频率估计值。这样循环迭代下去，频率估计的结果也会逐渐收敛到一个相对较为精确的值。在每个循环中进行干扰剔除时，为了求得第q次迭代的值，本文又提出了两种不同的计算方法：（1）利用上一次迭代中的计算出的干扰系数；（2）只利用由计算出的干扰系数，不用上一次迭代中的值。具体的详细步骤如表1 和表2 所示。

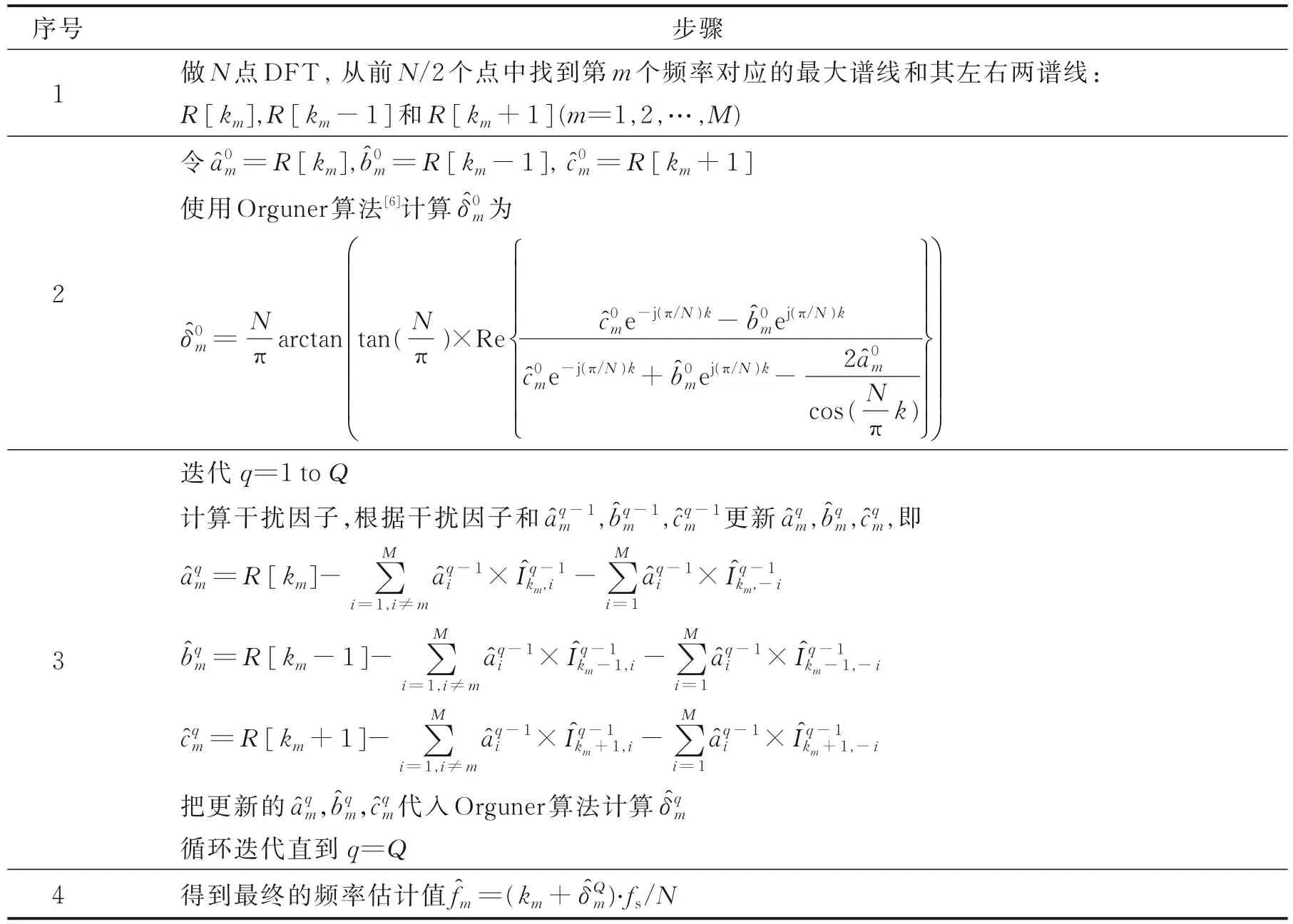
表1 多频频率估计算法1 步骤Table 1 Procedure of Algorithm 1

表2 多频频率估计算法2 步骤Table 2 Procedure of Algorithm 2

3 仿真结果与分析

本文研究了两种多频迭代算法的收敛速度。仿真模拟了无噪声情况下同时对2 个频率进行频率估计的场景，其中1 个频率固定为f1=20 kHz，另一个频率f2的变化范围为40～80 kHz。仿真中用两个不同频率的正弦波模拟两个频率的信号，采样速率设置为200 kHz，采样点数N为64。仿真共进行5 次迭代，实验中记录每一次迭代后的结果。图1，2 为算法1 和算法2 对2 个频率（f1和f2）进行频率估计的结果。从图中可以看出，算法1 和算法2 均在3 次迭代后达到稳定状态，因此基于计算复杂度考虑，后续仿真均使用3 次迭代。另外，比较图1 和2 可以看出，算法1 相比算法2 的最终收敛误差更小，因此后文与其他算法比较时均使用效果更好的算法1。

图3 仿真比较了本文提出多频频率估计算法和 Orguner 算法［6］、Borkowski 算法［10］、新三点法［9］在无噪声情况下的测量误差。Orguner 算法是用于复指数频谱估计的最精确的方法之一；新三点法是Bele‑ga 等人在MSD 窗经典三点法基础上提出来的，专门用于负频谱的干扰抑制；Borkowski 算法是电力系统频率估计中提出的一种性能较好的方法。仿真模拟了无噪声情况下同时对2 个频率进行频率估计的场景，其中一个频率固定为f1=20 kHz，另一个频率f2的变化范围为40～80 kHz。仿真中用2 个不同频率的正弦波模拟2 个频率的信号，采样速率设置为200 kHz，采样点数N为64。从图中可以看出，相比上述几种算法，本文提出的算法有更高的测量精度。

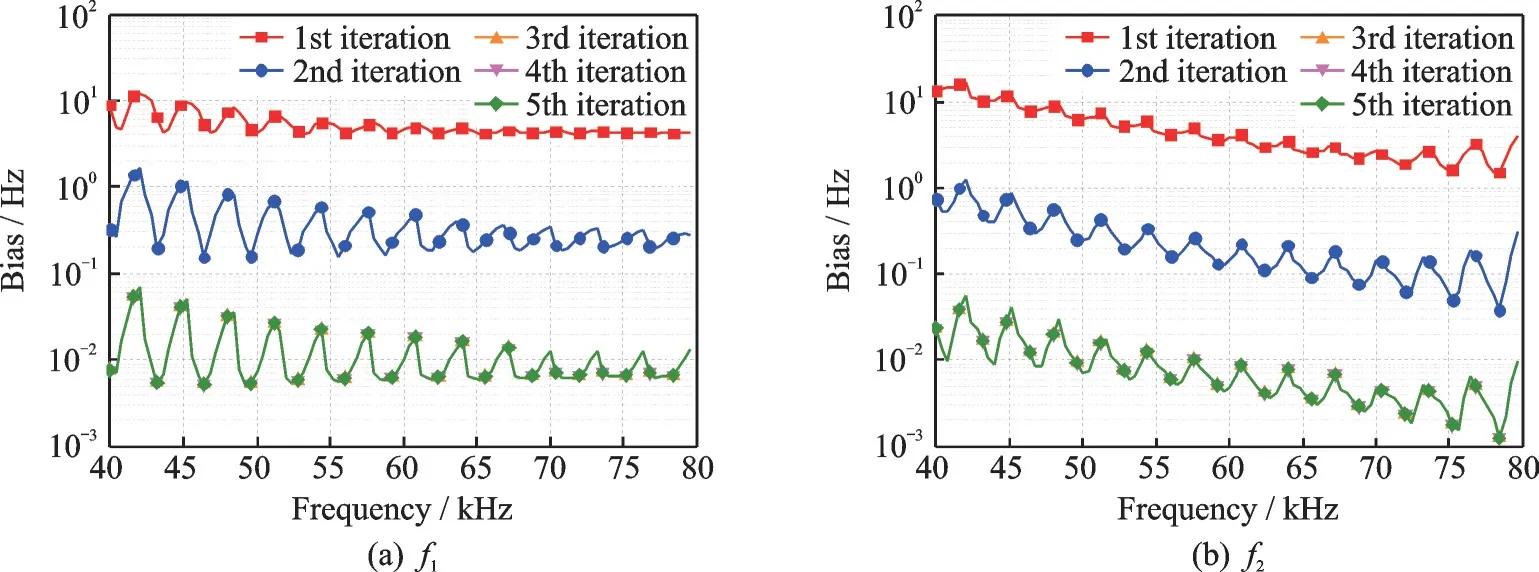
图1 算法1 中测量误差随频率2 变化情况（N=64）Fig.1 Frequency estimation error versus the frequency of f2 for different numbers of iteration by Algorithm 1 (N=64)

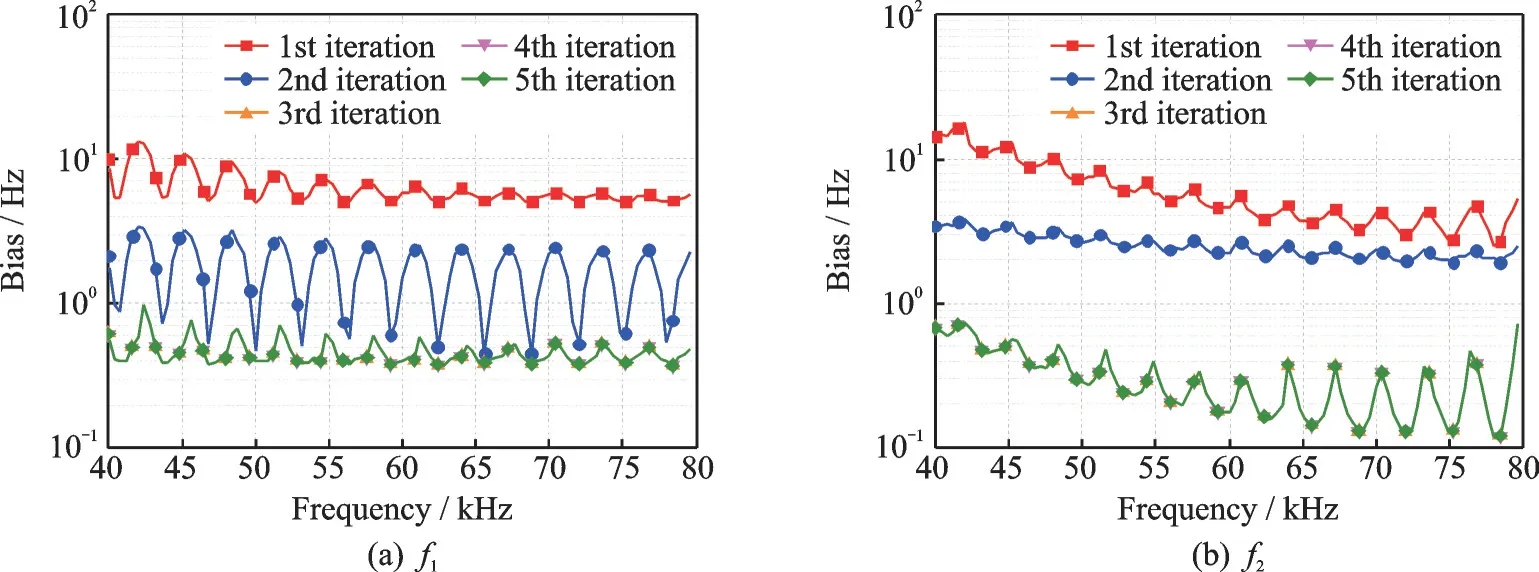
图2 算法2 中测量误差随频率2 变化情况（N=64）Fig.2 Frequency estimation error versus the frequency of f2 for different numbers of iteration for Algorithm 2 (N=64)

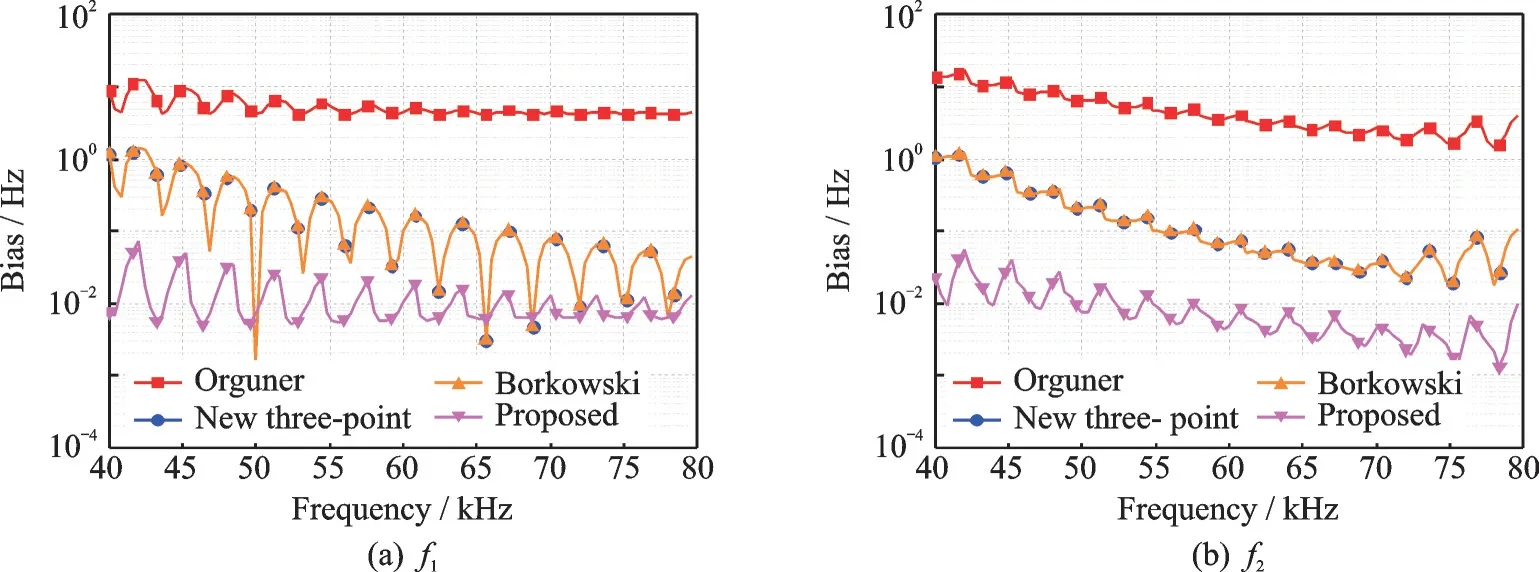
图3 无噪声时使用不同算法测量误差随频率2 变化情况（N=64）Fig.3 Frequency estimation error versus the frequency of f2 for different algorithms without noise (N=64)

本文接下来研究了在有噪声情况下各方法频率估计的结果（假设噪声为高斯白噪声）。仿真模拟了40 dB 信噪比下同时对2 个频率进行频率估计的场景，其中一个频率固定为f1=20 kHz，另一个频率f2的变化范围为40～80 kHz。仿真中用2 个不同频率的正弦波模拟2 个频率的信号，噪声为高斯白噪声，采样速率设置为200 kHz，采样点数N为64。图4 比较了各算法的均方根误差（Root mean square error，RMSE）。从图中可以看出，本文提出算法在有噪声情况下相比其他算法依然有优势。这是因为本文方法没有使用窗函数，避免了窗函数引起的信噪比损失［14］，而且本文方法不需要进行加窗处理，因此也减轻了计算复杂度的负担。

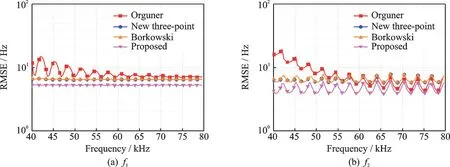
图4 信噪比40 dB 时测量误差RMSE 随频率2 变换情况（N=64）Fig.4 RMSE versus the frequency of f2 for different algorithms with SNR=40 dB (N=64)

本文算法在精度上有提升主要有两个原因。（1）该算法充分考虑了频率估计误差的来源（负频率干扰和其他频率干扰），并通过详细的数学推导得到干扰项的数学表达式，进而通过迭代的方法进行干扰的剔除。相比之下，传统的加窗算法只是通过窗函数尽量抑制频谱的副瓣，干扰的抑制效果不如本文算法。（2）窗函数会带来信噪比的损失，本文算法没有用到窗函数，也因此避免了信噪比损失带来的精度下降。本文算法在计算效率方面有提升主要体现在少了与窗函数相乘这一环节，减少了计算量。代价是迭代的次数如果太多，也会增加计算量。但是本文证明，算法经过3 次迭代即可收敛，迭代增加的计算量很小，因此总体来说本文算法在计算效率方面有所提升。

4 结束语

针对FMCW 雷达测距中遇到的多频频率估计问题，本文在Orguner 算法的基础上利用迭代的手段，逐步消除负频谱和其他频率带来的干扰，最终实现了较为精确的频率估计。本文设计了2 种迭代方法并通过比较选择了效果更佳的方法，该方法与传统频率估计方法相比，无论在估计精度上还是计算复杂度上都有明显优势。