基于STFT‑SST 和深度卷积网络的多相码雷达信号识别

倪 雪，王华力，徐志军，荣传振

（陆军工程大学通信工程学院，南京，210007）

引 言

多相码信号由于具有较低的自相关函数旁瓣电平、较大的多普勒容限和较好的低截获性，在低截获（Low probability of intercept，LPI）雷达中得到了广泛应用［1］。多相码是对连续载波进行相位调制，不同的相位序列产生不同类型的多相码，其中Frank 、P1 和P2 码由步进线性调频信号近似而来，P3 和P4 码由线性调频信号近似而来。可见，多相码信号属于线性调频类信号，不同类型的多相码信号之间具有高度的相似性，类间差距小，使得多相码在识别时极易相互混淆，尤其在低信噪比（Signal‑to‑noise ratio，SNR）下，多相码信号往往识别率很低，这给当前电子侦察设备的识别工作带来了巨大的挑战。因此，研究多相码雷达信号的分类识别问题成为了当前电子侦察领域的研究重点。

选取有效的特征参数，表征出信号之间的差异，是多相码LPI 雷达信号正确识别的重要因素。不少学者提出将高阶谱特征、时频特征等应用到LPI 雷达信号的检测识别中，取得了一定的成效［2‑4］。文献［2，4］选取信号的双谱对角切片作为调制识别的特征参数，保留了信号的幅度与相位信息。文献［5‑7］选取 Choi‑Williams 时频分析（Choi‑Williams distribution，CWD），并结合裁剪、缩放及二值化等图像处理等方法获取信号的时频特征用于识别。CWD 分析作为一种有效的时频分析方法，具有较高的时频聚集性，又尽可能地克服了交叉项干扰，被广泛用于LPI 雷达信号识别。但是CWD 时频分辨率有限，细节信息描述欠佳，不能有效体现出信号之间的细微差别，且CWD 算法复杂，实际中不易实现。同时，图像二值化使得细节特征丢失，在低SNR 下对多相码的识别效果并不理想。为了降低信号的噪声，文献［8］提出采用样本平均技术（Sample averaging technique，SAT）对信号进行去噪预处理，对CWD 时频分析后的图像进行裁剪和缩放，以灰度图像作为信号的特征描述。在低SNR 条件下，取得了较佳的识别效果。但是该方法需要提高信号采样率，对硬件设备的要求较高。若不考虑去噪预处理，对Frank、P1～P4 五种多相码的识别精度为90.2%。在识别算法中，文献［2］选用深度置信网络用作信号识别；文献［4，6‑8］选用深度卷积神经网络用作信号的分类识别；文献［5］采用栈式自编码网络和支持向量机方法用于解决识别问题；文献［9］选用SSD 和辅助分类器用于解决不同类型的LPI 雷达信号识别问题。综上，深度学习网络用于LPI 雷达信号的分类识别取得了不错的成效。

2014 年，Thomas 等提出了同步挤压短时傅里叶变换（Short‑time Fourier transform‑based synch‑rosqueezing transform，STFT‑SST）方法［10］。作为一种新的时频分析方法，STFT‑SST 利用同步挤压变换方法［11］，在短时傅里叶变换变换的基础上，将信号时频谱上的能量进行重新排列，使之聚集到信号的真实瞬时频率附近，以达到“挤压”的目的，从而获得具有更高分辨率的时频图。文献［12］将STFT‑SST 用于非平稳信号分离，取得了较好的效果。相比CWD 等时频分析，STFT‑SST 具有更优的时频聚集性，为LPI 雷达信号的时频分析提供了一种有效的方法。然而，挤压后的时频谱在低SNR 下特征细弱，不利于识别。针对特征相似的多相码信号，如何设计网络结构，提升网络对信号细节的表征能力，提高识别精度还值得进一步研究。

因此，本文采用同步挤压短时傅里叶变换对多相码信号进行时频分析，并提出了一种频谱增强算法，提高信号在低SNR 下的时频特征表征能力，获得高分辨率的时频特征图像。在识别网络设计中，在卷积神经网络中引入Inception模块，使得网络能够捕获不同尺度下信号的细节特征，从而增强网络的特征提取能力，实现多相码LPI雷达信号的自动分类，从而解决多相码LPI雷达信号提取特征困难、识别率低的问题。

1 STFT‑SST 时频分析及处理

1.1 STFT‑SST 时频分析

多相码LPI 雷达信号可表示为

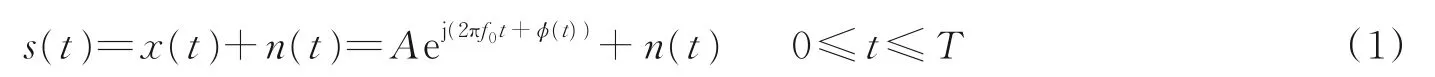
式中：A为信号幅度，f0为信号载频，T为编码周期，n(t)为高斯白噪声，ϕ(t)为相位调制函数，不同的相位调制函数表示不同的多相码LPI 雷达信号。

根据短时傅里叶变换定义，信号s(t)的短时傅里叶变换如下

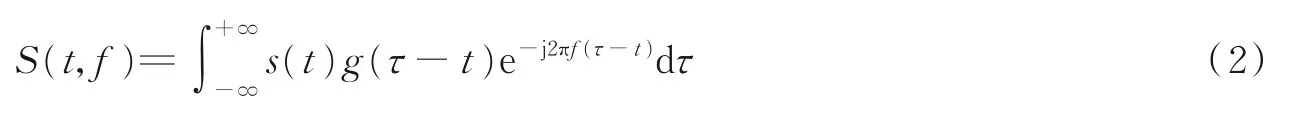
式中：S(t，f)为信号s(t)的时频谱，t为时间，f为频率，g(t)为窗函数。由于受窗口大小的限制，短时傅里叶变换的频率分辨率不能达到最优，其真实瞬时频率附近存在一定宽度的伪频率成分。通过对S(t，f)求导，可计算其瞬时频率其表达式如下

式中：i 为虚数单位。根据同步挤压原理，将变换系数S(t，f)按照建立映射关系，对某一频率区间内的频谱进行叠加，使能量集中到实际瞬时频率上，以提高频率分辨率。因此，信号s(t)同步挤压短时傅里叶变换的定义为

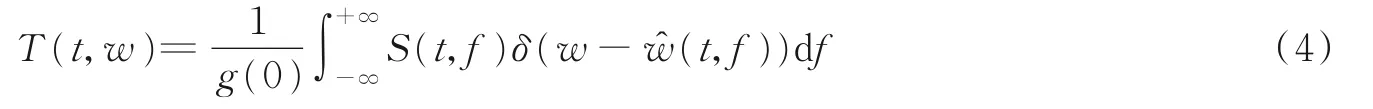
式中：δ为狄拉克函数，g(0)表示t=0 时窗函数的值。这里，g(t)选取的是长度为256，参数为10 的Kai‑ser窗函数。设信号的长度为L，则经过STFT‑SST 时频分析后，可得到大小为256×L的时频图像。

多相码的时频图呈近似线性调频信号的线段特点。挤压之前，线段较宽、较模糊；经过挤压后，线段更为精细，细节信息更清晰。同时，噪声在挤压过程中出现了一定程度的弱化。可见，采用STFT‑SST 时频分析不仅提高了时频图像的分辨率，而且还抑制了部分噪声，有利于后续信号的正确识别。

1.2 频谱增强及处理

考虑到挤压后的时频特征信息精而少，在较低SNR 条件下，这些信息极易受严重的噪声干扰而变弱。为了在低SNR 下尽可能地增强时频特征，进一步提升识别性能，本文提出了一种频谱增强技术，将信号的时频谱T(t，w)沿着小频率范围内[-Δw，Δw]进行频移再叠加，其表达式为

信号经过STFT‑SST 后的时频特征全部集中到时频图像的上半部分，采用图像裁剪技术，保留一半大小包含特征信息的时频图像；再采用最近邻插值技术实现时频特征降维，使得降维后的时频特征图像大小为128像素×128像素。最后，将降维后的时频图进行归一化处理，得到标准化的时频图像，作为识别网络的输入。信号整个时频特征分析及处理过程如图1 所示。图2 为增强的STFT‑SST 时频图和CWD 时频图的对比。可以看出，增强后的STFT‑SST 时频图像特征更为丰富、显著。

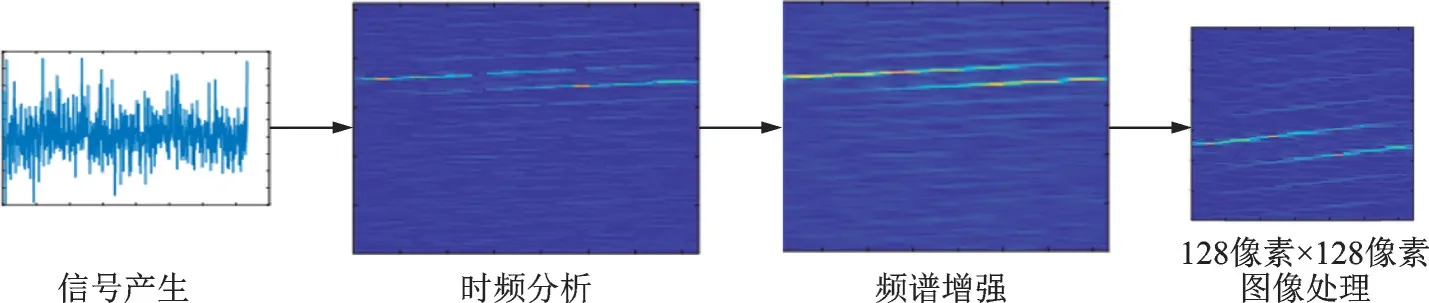
图1 雷达信号时频分析及处理Fig.1 Radar signal time-frequency analysis and processing

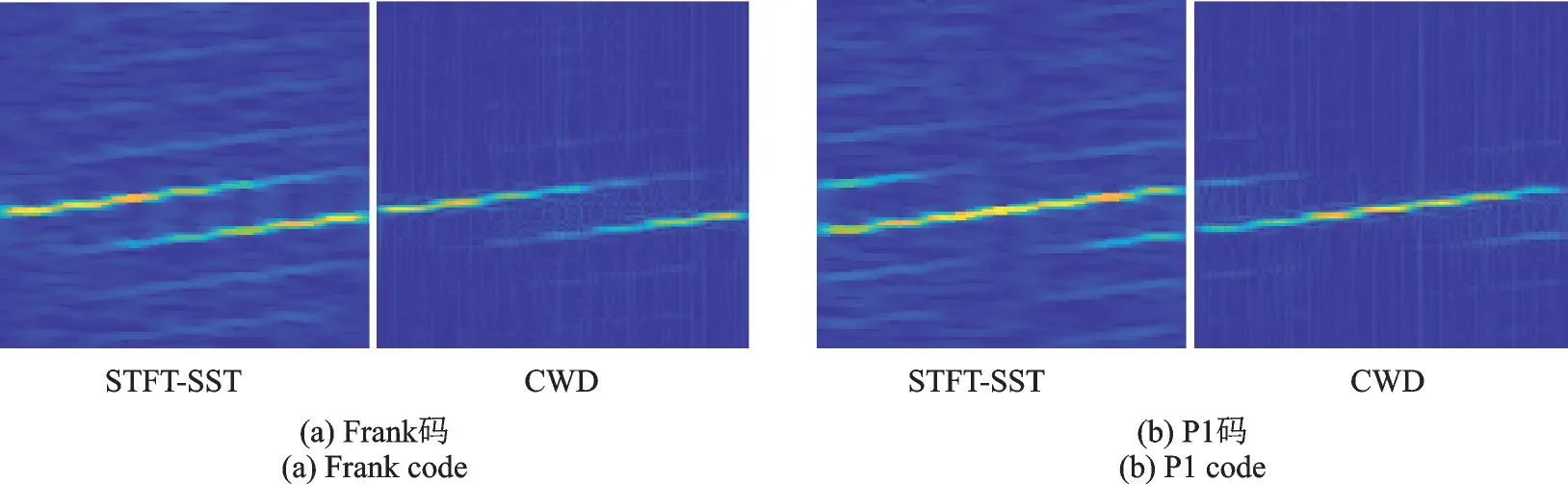
图2 增强STFT-SST 和CWD 时频图像对比（SNR=10 dB）Fig.2 Enhanced STFT-SST and CWD time-frequency image comparison（SNR=10 dB）

2 基于深度卷积网络的多相码LPI 雷达信号识别

2.1 深度卷积网络构建

卷积神经网络（Convolutional neural network，CNN）的基本结构是由输入层、卷积层、池化层、全连接层、分类层和输出层等相互连接组合而成，通过多个不同尺度的卷积和池化操作，逐层对输入信息进行特征变换，并利用反向传播算法对网络进行训练，实现参数的自动更新，自动地学习提取各个层次的特征，最后通过分类算法实现目标的有效识别。近年来，CNN 网络在网络深度、结构和轻量化实现等方面都取得了不错的进展［13‑14］。

针对多相码雷达信号时频图像的特点，本文设计了一个9 层深度卷积网络，如图3 所示。其网络架构由输入层、3 个卷积层、2 个池化层、1 个 Inception 模块、1个全连接层和分类输出层组成。输入层为128像素×128像素大小的时频图像；卷积层中，1，2，3 层卷积核大小分别为 7× 7，5× 5 和 3× 3，数量分别为 64，64 和96，stride 大小为1。每一个卷积层后都连接着批归一化（Batch normalization，BN）层，并采用修正线性单元（Rectified linear unit，ReLU）作为激活函数。池化层中，采用的 Maxpool，池化窗口大小为 2× 2，stride 为2 。为了提升网络对细节特征的捕获能力，网络设计中加入了Inception 模块。通过不同尺度的卷积核并列堆叠在一起，拓宽了网络的宽度，增强了网络的特征提取能力。Inception 模块包含大小为 1×1，3×3，5×5的卷积核和3×3 的池化，stride 取值设为1，并采用2 个1×5 和 5×1 的卷积核替代传统 5×5 的卷积核，以降低参数数量，提高网络的速度。需要注意的是，Incep‑tion 模块中的卷积层后面没有连接BN 层。最后将各通道输出进行Concat，实现多个特征的串联，并将串联后的特征送入全连接层。输出采用softmax 函数实现信号的分类判别。

图3 深度卷积网络结构Fig.3 Deep convolutional network structure

2.2 多相码雷达信号识别算法

结合同步挤压短时傅里叶变换和深度卷积网络，本文提出的多相码雷达信号识别算法主要分为3阶段。

阶段1利用同步挤压短时傅里叶变换对含噪的多相码雷达信号进行时频分析，并进行频谱增强处理，获取信号的高分辨增强时频图像；采用剪切、插值和归一化预处理方法实现特征图的数据降维。

阶段2将预处理后的时频图像分成训练数据和测试数据两部分，将训练数据送入构建好的深度卷积网络模型进行训练。

阶段3将测试数据送入训练好的网络模型中，通过入softmax 分类器进行分类输出，从而实现信号的自动分类识别。

算法流程图如图4 所示。

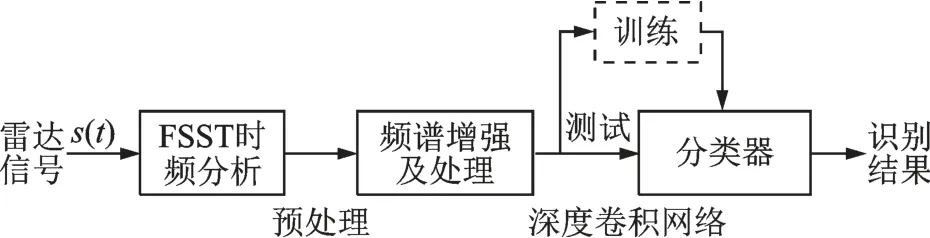
图4 多相码雷达信号识别算法流程图Fig.4 Recognition algorithm flowchart of polyphase codes radar signal

3 实验结果与分析

3.1 实验设置

仿真实验使用5 种多相码LPI 雷达信号，分别是：Frank、P1、P2、P3和P4。每种信号的参数设置如表1 所示。设采样频率fs=20 MHz，信号的载频f0取值范围为[fs/5，fs/4]，M为步进频率（整数），Nc为子码数，cpp 为子码周期数。设信号的SNR 取值范围为-10～10 dB，步长2 dB。每种信号共产生2 200 个总样本，其中1 540 个（70%）作为训练集，660 个（30%）作为测试集。

实验在 PC 机上完成，配置如下：CPU 为 i7‑7820HK（2.9 GB），内存为6 GB、GPU 为Nvidia GeForce GTX1080。网络训练时选用交叉熵损失函数，SGDM 优化算法，初始学习率为0.01，epoch 取值为10，迭代次数为600 次。为了保证实验结果的可靠性，取20 次实验的平均值作为最终的识别结果。

表1 多相码LPI 雷达信号参数Table 1 Parameters of polyphase codes radar signal

3.2 不同SNR 下识别性能分析

为了验证本文算法在低SNR 条件下识别的有效性，将STFT‑SST 算法、增强的STFT‑SST 算法与经典的CWD 算法进行了识别性能的对比。从运行时间看，单个信号执行一次CWD 算法耗时需要15 s以上，而执行一下 STFT‑SST 算法以及增强的 STFT‑SST 算法仅需 0.2 s 左右。可见，STFT‑SST 算法的运算速度更快。3 种时频分析方法均采用设计的深度卷积网络进行识别，各种算法在-10～0 dB下的识别率如图5 所示。

由图5（a）可以看出，随着SNR 的减小，5 种多相码识别准确率逐步降低。当SNR 大于-6 dB 时，3种算法的整体识别率均超过93.5%，识别效果较好。其中，STFT‑SST 算法的整体识别率与CWD 算法基本接近，而增强的STFT‑SST 算法识别率略高于CWD 算法。当SNR 小于-6 dB 时，整体识别率下降较为明显。STFT‑SST 算法和增强后的STFT‑SST 算法的整体识别率均明显高于CWD 算法。在SNR 为-8 dB 时，3 种算法的整体识别率分别为90.2%，91.8%，88.0%。这说明采用STFT‑SST 时频分析在低SNR 条件下的识别性能更具优势，并且使用频谱增强后的STFT‑SST 可以进一步提升识别准确率。由图5（b—f）单个信号的识别结果来看，P2码的识别效果最佳，其特征明显区别于其他信号，在低SNR 下也易于识别。Frank 和P3码的识别性能次之。当SNR=-10 dB 时，STFT‑SST 算法对以上3 种信号的识别率可达90% 以上，相比文献［6，8］中的方法，性能有着明显的提升。P1和P4的识别精度最低，两者的时频特征都为多条相似的直线，差别仅在于直线有无细微的阶梯状特点。在 SNR 为-10 dB 条件下下，相比 CWD 算法，增强的STFT‑SST 算法的识别精度可提高8～10 dB。这表明本文提出的算法在低SNR 条件下可获得更好的识别性能。表2 给出了-8 dB 下采用增强的STFT‑SST 算法对5 种多相码的识别结果，其中，P3码容易被误识别为 Frank 码，而P1码和P4码容易相互混淆。

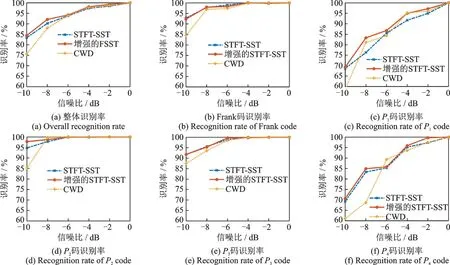
图5 不同SNR 下多相码识别率Fig.5 Recognition rates of polyphase codes under different SNRs

表2 -8 dB 下5 种多相码的识别结果（增强的STFT‑SST 算法）Table 2 Recognition results of five kinds of polyphase codes at SNR of -8 dB（enhanced STFT‑SST algorithm）

4 结束语

本文提出一种基于同步挤压傅里叶变换和深度卷积网络的多相码LPI 雷达信号识别算法。采用同步挤压傅里叶变换对信号进行时频分析，并通过频谱增强技术，提升了低SNR 下时频特征的表征能力。在识别网络中，引入Inception 模块，使网络能够捕获不同尺度下信号的细节特征，增强网络的特征提取能力。实验仿真表明，在低SNR 条件下，该方法可以有效地提高多相码的识别准确率，识别性能优于传统的基于CWD 的分类算法，且算法速度快，易于实现，为实际LPI 雷达信号的识别提供了一种解决方案。