内插倍数可变的低滚降成形滤波器的设计与实现
2020-12-18周士雷倪永婧
周士雷,倪永婧
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.河北科技大学 信息科学与工程学院,河北 石家庄 050000;3.燕山大学 信息科学与工程学院,河北 秦皇岛 066000)
0 引言
卫星通信具有覆盖范围广、不受地理环境限制和对抗自然灾害能力优异等优势,因此获得了越来越广泛的应用,传输业务量也越来越大。同时,卫星通信骨干网的信息传输呈现高速化趋势,对卫星带宽提出了更高要求[1]。文献[2-8]论述了在卫星通信系统中,由于星上转发器资源功率和带宽双重限制,转发器资源租用价格昂贵,因此充分高效利用转发器的资源是提升卫星通信系统能力的关键。文献[9-10]论述了调制解调器在卫星通信系统中的作用。在卫星通信系统中,调制解调器主要完成业务数据和模拟中频信号的变换,是充分高效利用转发器资源和提升卫星通信系统能力的关键设备。业务终端设备的数据流经过组帧、信道编码、星座映射、成形滤波、基带调制及变频等处理后输出中频信号至上变频设备,同时把经由下变频送至设备的中频信号经过解调及译码等处理后,送至业务终端。
卫星调制解调器的设计中,大部分调制方式都可以通过正交调制的方式实现,即可以利用正交基带信号对载波参数进行调制,不同的载波调制方式对应不同的正交基带波形[11]。各种调制方式,在符号跳变的时刻,调制载波发生突变,从而导致调制载波频谱的扩展,造成相邻信道的干扰[12]。为解决这一问题,对基带调制信号进行成形滤波。目前,卫星通信常用的是平方根升余弦滤波器,成形系数为0.3。在实际通信中,成形系数越低,信号所占带宽越小[13]。但是成形系数越低,需要的滤波器阶数越高,消耗的资源越多,尤其在符号速率逐比特可变的调制器(64 ksps~20 Msps)设计中,基带信号经成形滤波模块进行频谱成形后,为了滤除数字处理过程中产生的镜像分量,在DA变换之后需要一个模拟低通滤波器[14]。符号速率变化时,为了在不改动模拟滤波器的情况下实现对镜像分量的滤除,需要将抽样速率固定在一定范围内。最高速率需保证4倍符号速率,低速率所需成形倍数达到1 024倍符号速率,针对在实际应用中成形系数为0.05时,传统设计需要近万的乘法器资源,实现复杂度较高的问题,本文提出一种内插倍数可变低滚降成形滤波器的设计与实现方法,在实现低滚降成形的基础上大大降低了实现消耗乘法器资源,为实现低滚降成形系数工程实现奠定了基础。
1 成形滤波器设计原理
成形滤波器主要是将信号频谱限定在一定范围内以提高频谱利用率,同时降低系统误码率,它必须满足奈奎斯特第一准则[15]。满足奈奎斯特准则的滤波器有很多,如理想低通、升余弦滚降、直线滚降及三角特性等。其中,理想低通滤波器频带利用率最高,可达2 Baud/Hz。但理想低通在物理上是无法实现的,而且这种滤波器时域响应波形尾巴震荡幅度大,一旦定时稍有偏差,会出现严重的码间干扰。因此,在实际应用中,对理想低通滤波器的边沿做缓慢下降处理,一般采用根升余弦滚降特性滤波器完成成形滤波,其传递函数为:
(1)
式中,fN=Rs/2=1/2Ts为信道符号速率的一半。发射RF载波频谱要求相对于调制器输出频谱不应倒置。
工程实现时,必须对滤波器进行截短处理。在FPGA实现时需要对滤波器进行取整处理[16],取整和截短造成旁瓣升高及滚降特性变差等,这就需要合理确定截短的长度。
2 低滚降成形内插滤波器的设计
在符号速率逐比特可变调制器设计中,信道编码成帧后的数据经过成形滤波器进入DA芯片,进行数模变换,变换后的模拟信号经过基带滤波器滤除镜像分量,然后进行中频调制,生成中频信号输出。基带滤波器一般采用模拟低通滤波器实现,为了实现模拟低通滤波器对各个符号速率的镜像分量的滤除,需要把DA的采样钟限定到一定范围内,一般情况采样钟的频率需大于基带滤波器的带宽。为了匹配符号钟和采样钟的关系,需要不同数据速率采用不同的内插倍数,低速高内插倍数,高速低内插倍数。调制信号处理流程如图1所示。

图1 调制信号处理流程Fig.1 Modulation signal processing
调制器的最低符号速率为64 ksps,设计的基带模拟滤波器的带宽为20 MHz,采样钟在25~100 MHz逐Hz可变,成形滤波器需要支持最大512倍内插,最小4倍内插。成形滤波器时域表达为:
(2)
式中,T为每个符号的周期;α为滚降系数。
实际工程中,必须对上述滤波器进行截短处理。滤波器进行截短处理后,会产生吉布斯效应,直接影响滤波器的性能。降低吉布斯效应通常的做法是增加滤波器的长度[17]。
实际设计滤波器涉及内插倍数IP、截短长度GN和滤波器阶数N。IP为滤波器响应在每个码元周期内的采样点数;GN为截短的滤波器的时域长度(以码元周期T为单位);N=GN×IP,如果增加滤波器的阶数,则相应地增加了实现其滤波器的乘法器数量。
理想滤波器是不存在的[18]。实际系统中,滤波器都是经过截短处理,通过增大IP而不改变GN,不影响滤波器的滚降特性,即通过增加采样时钟,提升内插倍数而增加数字N的方法,不能压低第一旁瓣。
不同内插倍数根升余弦滤波器的频谱对比如图2所示,点划线代表IP=4,GN=8T,α=0.05的频谱图,实线代表IP=8,GN=8T,α=0.05的频谱图,可以看出,2条谱线重叠。由此可知,不改变截短长度,改变内插倍数不影响滤波器的特性。

图2 不同内插倍数根升余弦滤波器的频谱对比Fig.2 Spectrum comparison of square root raised-cosine filter with different interpolation multiples
不同截短长度根升余弦滤波器的频谱对比如图3所示。

图3 不同截短长度根升余弦滤波器的频谱对比Fig.3 Spectrum comparison of square root raised-cosine filter with different truncation lengths
细点划线代表IP=4,GN=8T,α=0.05的频谱图;细点虚线代表IP=4,GN=16T,α=0.05的频谱图;粗实线代表IP=4,GN=32T,α=0.05的频谱图;粗点实线代表IP=4,GN=64T,α=0.05的频谱图。由图3可以看出,提升群时延可以提升滤波器的滚降特性,但是当GN由32T提升至64T时,效果不明显。综合以上2点设计低滚降成形滤波器采取GN=32T进行设计。最大滤波器阶数为512×32=16 384,阶数巨大,需要的乘法器非常多,普通数字信号处理芯片不能实现。
3 结合激励特点的多相滤波技术
实际工程应用中,为了减少内插成形滤波器中乘法器的资源消耗和计算量,常常结合输入激励特点,对其进行多相分解,指将数字滤波器的转移函数H(z)分解成若干个不同相位的组。成形滤波器h(n)采用有限冲击响应(FIR)结构实现,其z变换为:
(3)
式中,N为滤波器长度。
若将h(n)的抽头分成L组,假设N是L的Q倍,即N/L=Q,Q为整数,其代表最大的内插倍数,那么H(z)的多相分解结构为:
H(z)=h(0)z0+h(Q)z-Q+…+h[(L-1)Q]z-(L-1)Q+
h(1)z-1+h(Q+1)z-(Q+1)+…+
h[(L-1)Q+1]z-(L-1)Q-1+
h(2)z-2+h(Q+2)z-(Q+1)+…+
h[(L-1)Q+2]z-(L-1)Q-2+…+
h(Q-1)z-(Q-1)+h(2Q+2)z-(2Q-1)+…+
h[(L-1)Q+Q-1]z-(L-1)Q-(Q-1)=
(4)
(5)
则:
(6)
式中,Ek(zQ)为H(z)的多相分量。
成形滤波器输入的序列为x(n),x(n)经过I倍内插之后为xI(n),输出为y(n)。
(7)
假定成形滤波器输入的序列为x(n),x(n)经过8倍内插之后为xI(n),其输入序列仿真如图4所示。输入的激励大部分点为0,可将输入激励的特点与多相滤波器的结构相结合节约乘法器资源。
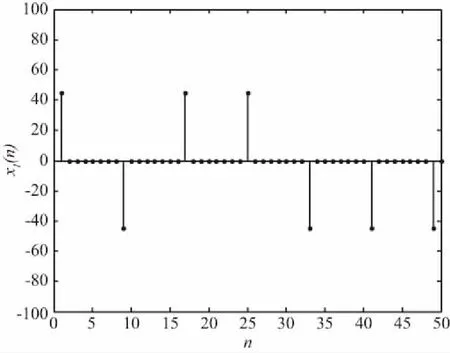
图4 内插后的输入序列仿真Fig.4 Interpolated input sequence
根据成形滤波器的多相分解,输入内插后的数据特点,并结合整数抽取,可明显节约乘法器资源。
多相成形滤波器的高效结构如图5所示。可以看出,每组输入的数据延时后分别抽取,抽取后分为I组,x1(n),x2(n),x3(n),…,xi(n),i=1,2,3,…,I,在这I组输入中,每个节拍必定只有一组输入激励不为0,其他I-1组输入激励为0,I-1组为0的激励卷积后的结果为0,I-1组滤波器不用工作,只有输入激励不为0那一组滤波器进行乘法运算,相当于每个节拍有32个乘法器工作。因此大大降低了乘法器资源的使用量,节省了数字信号处理器的资源。
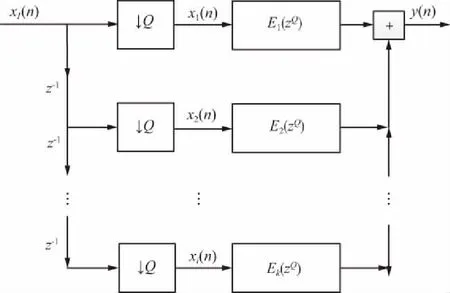
图5 多相成形滤波器的高效结构Fig.5 Efficient structure of multiphase forming filter
选用Altera公司Cyclone系列产品,选择以5CEFA9F23I7芯片作为处理核心器,设计了硬件实现平台。信号在编码成形后分为I,Q两路,分别送给低滚降成形滤波器进行成形滤波,需要2个低滚降成形滤波器,其实现原理如图6所示。成形滤波器共有32个乘法器,工作在成形钟下,乘法器的2个乘数分别为低滚降成形滤波器系数和成形滤波器的输入x(n),乘法器的结果进行相加输出为y(n)。
把通过Matlab生成的16 384个滤波器系数分为32组,每组512个系数,按顺序排列分别放进32个ROM中,地址生成器工作在成形钟下,通过内插倍数的地址步进,读出合适的内插系数组,即Ek(zQ),送进乘法器;x(n)工作在符号钟下进入移位寄存器,寄存的32个数据分别进入乘法器进行计算。乘法计算得出的结果相加得出滤波器计算结果。
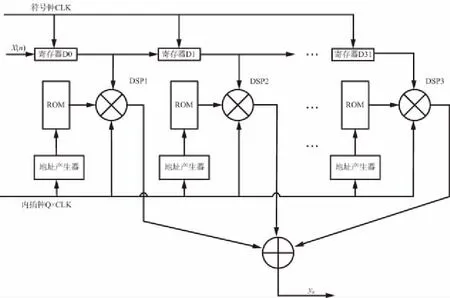
图6 低滚降内插滤波器实现原理Fig.6 Implementation principle of low roll-off factor shaping filter
通过控制内插成形钟与符号钟的比例关系确定内插滤波器的步进,实现了内插系数可变与多相滤波器技术相结合,在降低乘法器的使用量的同时实现了较大的信号变化范围。
4 性能测试结果与分析
上述基于多相滤波技术的内插系数可变的低滚降成形滤波器设计方法已在硬件平台上实现,其符号速率变化范围为64 ksps~20 Msps,并且其乘法器资源使用情况由传统方法估计的16 384个下降至32个,有效地实现了在较宽符号速率变化范围的同时降低了乘法器的使用量。成形系数为0.05带宽与传统成形系数为0.3的信号带宽对比如图7所示,成形系数为0.05的信号带宽有明显降低(3 dB信号带宽节省25%),可大大节省卫星资源。
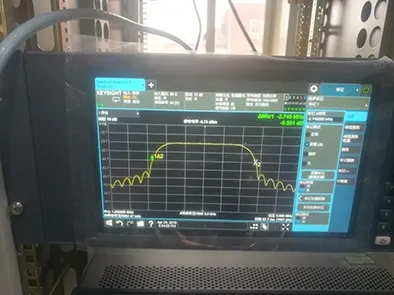
(a)成形系数0.30

(b)成形系数0.05
5 结束语
本文采用与输入激励相结合的多相滤波技术设计出内插倍数可变的低滚降成形滤波器与传统滤波器设计方案相比,占用的资源较少,实现简单;设计的低滚降滤波器与传统滤波器相比,大大降低了信号带宽,节约了卫星资源,已作为成熟技术应用于带宽可变的卫星通信终端设计中。
