基于AHP-Shapley值的城市轨道交通PPP项目风险分担研究*
2020-12-18王建波王政权黄文静
王建波 张 娜 王政权 黄文静 秦 娜
(青岛理工大学管理工程学院,266000,青岛)
随着我国经济发展水平的不断提升,严重的交通拥堵使得我国社会对轨道交通的需求量不断增加. 为满足居民日益增长的交通需求,很多城市陆续建立了多条城市轨道交通路线(以下简称城轨). 与其他交通形式相比,城轨项目的建设周期更长、施工难度更大,在实际建设过程当中需要大量资金支持,如果仅仅依靠财政资金将无法弥补国内各大城市城轨建设的巨大资金缺口,种种因素最终造成其发展进度缓慢. PPP(Public-Private Partnership)融资模式是政府与社会资本签署特许经营协议达成长期合作关系,政府与私营企业共同分担项目主要风险和利益的融资模式,将PPP模式引入到城轨建设中,不仅能稀释政府的财政压力,还能将风险分配到每一个参与方,对推动我国城轨项目的发展做出巨大贡献. 但是,目前我国城轨PPP项目的运作过程尚且缺乏经验,在全生命周期各阶段涉及众多风险. 因此,科学有效的城轨PPP项目风险分担对城市整体规划以及社会效益具有重要的意义.
目前,国内外很多学者针对PPP融资模式下的轨道交通风险分担展开了研究,K.C.Lam等从风险分担原则和专家意见等入手,利用模糊数学原理将其转化为量化的模型,通过模型求解来达到最优风险分担.[1]陶思平通过分析北京城轨PPP实际案例,结合过去几年国内外专家学者针对PPP项目风险分担的相关文献,提出了风险分担应遵循公正公平、有效控制、动态分担等原则.[2]在此基础上,有维宝等认为各参与方应根据自身承担风险的能力进行合理分担,如果所担风险超出了自身的可控范围,会对项目的整体效益造成不利影响,所以还需增加承担上限原则.[3]谭兵通过分析芜湖城轨交通PPP项目的具体情况,依据调查问卷结果,计算出了政府与社会资本在项目中各自的风险承担成本以及总的风险分担比例.[4]
在以上已有的研究中,鲜少有文献对PPP项目中政府和社会资本共担的风险给出一个最优的分担比例. 本文运用合作博弈思想为基础构建模型,首先对城轨PPP项目的风险从全生命周期各个阶段进行识别,从而找出共担风险,并利用Shapley值法按照各参与方对总目标的贡献程度进行初步分担,得到唯一解;然后,考虑公司双方风险分担能力,利用AHP法计算影响风险分担的因素的权重,对初步分担结果进行调整优化,得到修正后的风险分担比例;最后,结合青岛地铁4号线PPP项目,以不可抗力风险为例,得到最终风险分担比例,并对得到的结果进行分析评价.
1 城市轨道交通PPP项目风险识别
风险识别的准确程度往往决定分担结果的科学性,准确识别城轨PPP项目风险是最为关键的基础性工作,国内外很多专家学者针对城轨PPP项目的风险进行了识别,王凯妮等以青岛地铁4号线作为案例,将财务风险预警理论引入可行性缺口模型,对城轨PPP项目运营期的风险进行了识别.[5]盛立通过运用核对表法,对PPP模式下我国城轨的风险因素进行了分析整理,建立了哈尔滨地铁2号线项目风险指标体系.[6]邵江鲁在对风险进行全方面识别的基础上,进一步采用TFAHP法对公私合作模式下的城轨项目关键风险进行了识别研究.[7]结合前人研究经验,本文将风险划分为决策阶段、融资阶段、建设阶段、运营阶段以及全生命周期风险. 共识别出20项轨道交通PPP项目风险因素,风险识别的结果如图1所示.
2 城市轨道交通PPP项目风险分担
2.1 风险初步分担
在有两个或者两个以上主体共同参与的经济管理活动中,各利益相关方目标不一致是形成博弈行为的主要原因[8],城轨PPP项目也不例外,其初步风险分摊就是一个典型的政府部门和社会资本之间的合作博弈[9-10],通过博弈,希望能够在参与双方之间形成一个满意的风险初步分担方案,同时也为下面风险分担比例的确定打好基础.

(1)
(2)
则项目参与满意度为:
(3)
以公私双方对PPP项目风险j的分担情况为例进行博弈分析,双方判断自身是否具有对该风险的控制能力,从而作出“承担”或“不承担”2种选择,最终总共有4种组合情况,如表1所示.

表1 风险分担主体双方博弈模型
2.2 风险分担比例确定
2.2.1初始Shapley值的风险分担模型
博弈理论是通过对所要分析的问题进行判断,使决策对象之间相互作用、相互平衡,以至于达到结果最优化的理论. Shapley值是博弈理论的一个分支,它是由Shapley L S在1953年提出的,按照参与者对总目标的贡献程度将联盟产生的收益或是成本进行分配,它的优点在于可以得到一个确定的量化值,且为唯一解.[11]PPP模式中的风险分担是典型的合作博弈问题,可以采用Shapley值法求得PPP项目公私双方各自应承担的风险量.[12]该博弈模型中的Shapley值用φi(v)表示,则有:
(4)
2.2.2引入风险分担修正因子
城轨PPP项目的风险分担是一个复杂的过程,在项目周期中会受到一系列因素的影响.[13]因此为了最大限度地提高风险分担结果的可信度,本文根据风险分担的基本原则,系统全面的检索影响PPP项目风险分配的因素,从风险的认知能力、风险的承受能力和风险的承担意愿3个维度引入风险分担修正因子,对2.2.1中求得的Shapley值进行调整优化,具体的风险分担影响因素如表2所示.
2.2.3计算AHP方法修正后的风险分担比例
本文利用层次分析法(AHP) 对影响因子赋权. 在具体的计算过程中,先从下层开始计算,从风险发生诱因、风险发生概率、风险产生损失来判断风险认知能力,从偿债能力、风险准备金、盈利能力来判断风险承受能力,从风险偏好、风险管理成本、参与方主观感受来判断风险承担意愿,再根据风险认知能力、风险承受能力和风险承担意愿的权重来对初始Shapley值做出调整.
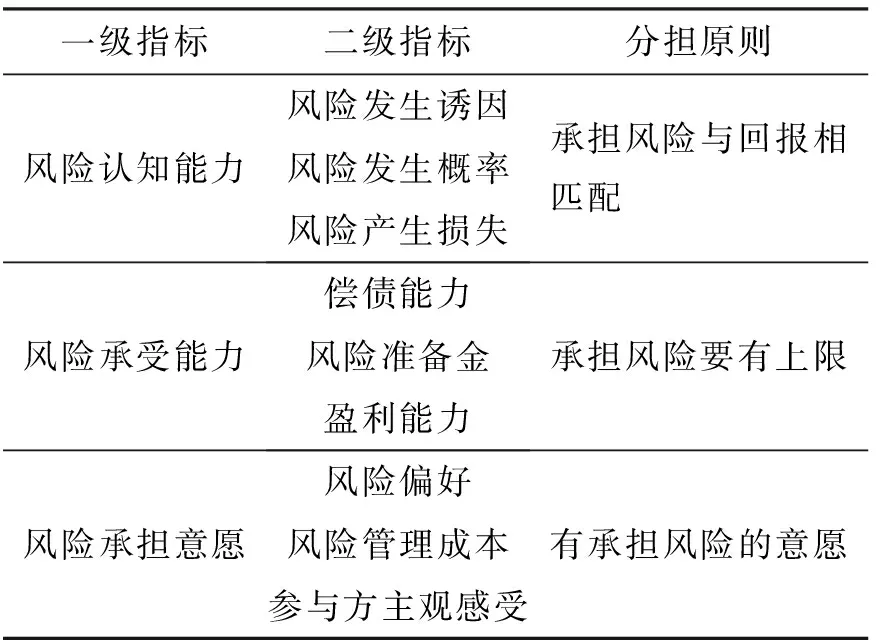
表2 城市轨道交通PPP项目风险分担影响因素
以风险认知能力为例,介绍具体的推导步骤. 对政府部门A和社会资本B的风险认知能力的影响因子为风险发生诱因、风险发生概率、风险产生损失,通过AHP法确定3个影响因子对公私双方风险认知度影响的权重,每个影响因子相对重要性的打分由从事相关研究的专家根据多年经验利用1~9标度法打出,最后求平均值得到每个指标的最后得分CA、PA、LA、CB、PB和LB. 从而计算出风险认知能力的得分结果分别为a1和b1. 因此在风险认知能力方面A 所占的比例为δA1=a1/(a1+b1).
在运用Shapley值进行风险初步分摊时,是假设公私双方在风险认知度上的比例各占1/2,所以调整因子为ΔA1=δA1-1/2. 如果ΔA1大于零,则表示政府部门需要在原始风险分配比例的基础上增加相应的额度,如果ΔA1小于零,代表政府部门需要在初始分担比例上减少相应的额度. 综上所述,在风险认知能力方面,政府部门需要调整的数额为ζA1=ΔA1(φ1+φ2)k1,同时社会资本需要调整的数额为ζB1=ΔB1(φ1+φ2)k1,很显然,ζA1+ζB1=0,其中k1,k2,k3分别是风险认知能力、风险承受能力以及风险承担意愿三者的权重. 因此对于政府部门A的调整额为ζA=ζA1+ζA2+ζA3,对于社会资本B的调整额为ζB=ζB1+ζB2+ζB3. 因此经过调整后的风险分担份额为α1=(φ1+ζA)/(φ1+φ2),α2=(φ2+ζB)/(φ1+φ2).
3 实例分析
3.1 案例概况
青岛地铁4号线是青岛市轨道交通在建的一条地铁线路,该线是连接主城区和崂山区的东西方向骨干线路. 全线东西两端站点分别为大河东站和人民会堂站,贯穿青岛三大主要市区,穿越各大旅游及人群密集站点,路线位置优越. 线路总长30.7 km,均为地下线,共设25座车站,其中换乘站10座,总投资额211.10亿元,预计于2021年底竣工运营,本节将根据第2节中提出的风险分担的步骤,从项目全生命周期的风险角度出发,对青岛地铁4号线进行详细的分析评价.
本文对从事城市轨道交通PPP项目的企业工作人员6人,政府部门有关人员4人,学者及研究人员10人进行了专家访谈,结合以往类似案例的项目管理经验,根据青岛地铁4号线项目施工过程中的实际情况进行项目管理的预测分析,当不可抗风险发生时,若不采取任何应对措施,预计会造成约6 000万元的项目亏损;如果公私合作双方合作共同采取措施应对风险,估计项目损失值为2 500万元;如果政府部门单独承担该风险,预计需要承担的损失值约为4 000万元;相反,若由社会资本方独自应对该风险,预计会造成约3 300万元的项目亏损额.
3.2 风险初步分担
在第1节中通过分析得到了20个城市轨道交通PPP项目关键风险因素,本文对其进行博弈分析,邀请5位在该领域具有丰富经验的专家分别对各指标进行打分,其中包括从事城市轨道交通PPP项目的企业工作人员2人、政府部门有关人员1人,以及高校从事PPP项目研究的专家学者2人,其中2人参与PPP项目的时间超过5年,其他3人参与时间为3~5年. 整理专家打分数据代入项目参与满意度函数中,得到风险初步分担结果. 风险因素清单及初步分担情况见表3.

表3 博弈分析
由政府部门承担的风险有:审批获得延误、土地获取、招标文件不完备、招投标竞争不公正、评标不合理、设计变更、法律变更、政府信用.
由私营机构承担的风险有:施工进度延迟、技术风险、建设成本超支、施工质量风险、运营主体经验不足. 需要共担的风险有:市场需求变化、项目唯一性、收费定价不合理、政策变化、不可抗力、税收调整、通货膨胀. 对共担风险利用AHP法修正的Shapley值法确定具体的风险分担比例.
3.3 风险分担比例确定
3.3.1初始Shapley值的风险分担模型
根据公式(4)分别计算政府部门和私营企业的原始Shapley值:
据此计算,双方承担风险分担的比例分别为40%和60%.
3.3.2计算AHP方法修正后的风险分担比例
本文设计了调查问卷,采用了电子邮件和现场问卷两种方式对3个一级指标以及风险认知能力一级指标下的3个二级指标按照1~9标度法进行打分. 问卷的主体包括针对每一种风险在不同参与方方面的39个问题,以及项目介绍以便于调查对象加深对本项目的了解程度,问卷发放的对象包括从事城市轨道交通PPP项目的企业工作人员6人,政府部门有关人员1份,学者及研究人员3份,其中3人参与PPP项目的时间超过5年,5人参与时间为3~5年,2人参与时间不足3年,总共发放了10份调查问卷,最终全部收回. 将所有有效问卷的专家打分值求平均数,最终得到需要的数据如表4、表5所示.

表4 一级指标判断矩阵
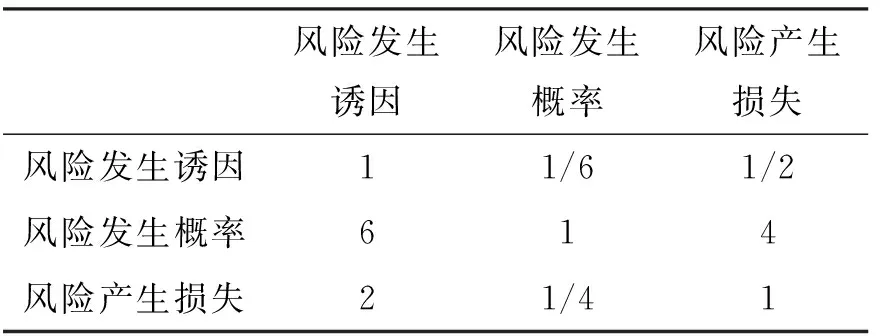
表5 二级指标判断矩阵
与上一部分的数据获取方法相同,对问卷调查结果中专家打分值求平均值得到针对各个主体在每个风险下与风险分担相关的9个影响因子打分如表6所示.
于是利用层次分析法可以求出政府部门方对项目不可抗力风险的风险认知能力得分YA1=6.47×0.11+5.43×0.70+6.19×0.19=5.69. 同理求出社会资本方对项目不可抗力风险的风险认知能力得分YB1=3.32.

表6 风险认知能力打分结果
因此在风险认知能力方面政府机构所占比例为δA1=YA1/(YA1+YB1)=0.63. 调整因子为ΔA1=δA1-1/2=0.13. 调整额为ζA1=ΔA1(φ1+φ2)K1=0.13×(1 400+2 100)×0.17=77.35. 社会资本所占比例为δB1=YB1/(YA1+YB1)=0.37. 调整因子ΔB1=δB1-1/2=-0.13. 调整额ζB1=ΔB1(φ1+φ2)K1=-0.13×(1 400+2 100)×0.17=-77.35. 同理可获得在风险承受能力方面政府部门调整额为200.2,社会资本调整额为-200.2. 在风险承担意愿方面政府部门调整额为150.15,社会资本调整额为-150.15.
因此,对于政府部门的总调整额为ζA=ζA1+ζA2+ζA3=427.7,对于社会资本的总调整额为ζB=ζB1+ζB2+ζB3=-427.7. 经过调整后的风险分担份额为α1=(φ1+ζA)/(φ1+φ2)=0.522 2,α2=(φ2+ζB)/(φ1+φ2)=0.477 8. 即在不可抗力风险方面政府部门承担的份额为0.522 2,社会资本承担的份额为0.477 8.
从得到的结果来看,在不可抗力风险方面,根据PPP项目风险认知能力、风险承受能力和风险承担意愿等影响因素优化后政府部门的风险分担额增加了427.7万元,同时,社会资本的风险分担额减少了427.7万元,大大提高了各参与方参与城市轨道交通PPP项目的积极性,有利于城轨PPP项目的顺利建设与运营.
4 结语
为保证城市轨道交通PPP项目的成功实施,本文对其全过程的风险进行识别. 并且基于合作博弈理论,结合问卷调查和专家访谈法,对项目参与双方应承担的风险进行合理划分,得到风险因素初步分担结果,明确了项目唯一性、不可抗力、政策变化等7个公私双方共担风险.
运用Shapley值法求得城轨PPP项目风险初步分担比例,得到公私双方承担风险的比例分别为40%和60%,引入风险认知能力、风险承受能力和风险承担意愿3个风险分担修正因子,使用层次分析法对其进行科学加权,对初步分担结果进行修正,使风险分担比例更加符合实际.
最终将风险分担模型应用于青岛地铁4号线PPP项目中,计算得到在不可抗力风险方面政府部门承担的份额为0.522 2,社会资本承担的份额为0.477 8,验证了基于AHP-Shapley值的风险分担比例确定模型的适用性. 本文所建模型验证了风险分担影响因素对分摊比例具有一定程度的影响,为类似城市轨道交通PPP项目的风险分担案例提供了一个新的解决思路.
