泰勒涡流流动及强化传热数值研究
2020-12-18牟军杰林海波童正明
叶 立,牟军杰,石 艳,林海波,童正明,岳 汉
(1. 上海理工大学 能源与动力工程学院,上海 200093;2. 过程装备与控制工程四川省高校重点实验室,四川 自贡 643000)
泰勒流[1]是介于层流和湍流之间的一种二次流动,在两个相对旋转的同轴圆筒间(通常为内圆筒旋转、外圆筒静止),随着内圆筒转速的增加,在离心力作用下在内圆筒轴线方向上诱导产生一系列有序排列的环形涡(即泰勒涡)。自1923年被发现以来,泰勒流就得到国内外学者广泛关注。早期研究主要针对不同条件下的流动图、流动稳定性等理论方面的研究,近期则更加重视不同操作参数下的流动模式及传热特性,以利于实际应用。
Backer 等[2]通过数值计算的方法分析了径向温度梯度对泰勒库特流稳定性的影响,研究结果显示,对旋转内圆筒表面加热能够增加泰勒库特流的稳定性,而对静止外圆筒表面加热会降低泰勒库特流的稳定性;黄为民等[3-4]采用粒子图像测速(PIV)测量技术对泰勒涡结构进行研究,对旋涡结构进行分析,从而解释泰勒涡的形成和发展机理。本课题组[5-6]将泰勒涡引入化工反应器中发现,涡流可在反应器中构建出平推流区域,在一定操作参数下平推流区域会随着转速增加而扩大,从而提高反应效率。
本文运用Fluent 软件,对长径比Γ=30 的同轴套管间涡流进行了数值模拟,并运用Tecplot后处理软件,得到流线、温度、热流及涡量等云图和数值结果,针对涡流形态的演变及其强化传热特性进行分析研究。这有助于理解泰勒涡流的多样性,也可为提高相关装置的传热效率提供参考依据。
1 建模和计算
1.1 物理模型和网格划分
长径比Γ的定义是筒体高度H与筒间环隙宽度δ之比,δ=R2-R1,R1、R2分别为内外圆筒的半径。本文模型中,H= 300 mm,R1= 40 mm,R2= 50 mm,Γ= 30,内圆筒旋转角速度为ω,内圆筒壁温T2、外圆筒壁温T1均恒定,分别为373、293 K。
利用结构化正交网格[7]对模型进行划分,网格径向、周向、轴向网格数分别为32、128 和512,网格总量为2 097 152。在内圆筒外壁面和外圆筒内壁面处进行网格加密[8],网格起始高度为0.005 mm,增长比为1.2,10 层加密网格。
1.2 控制方程
模拟泰勒涡流所用控制方程包括连续性方程、动量方程和能量方程,柱坐标系下三维NS 方程[9]为
连续性方程
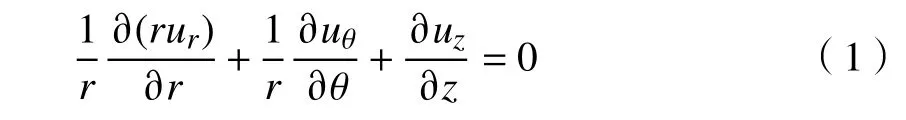
动量方程
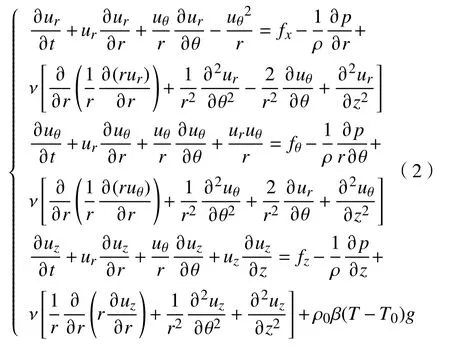
能量方程
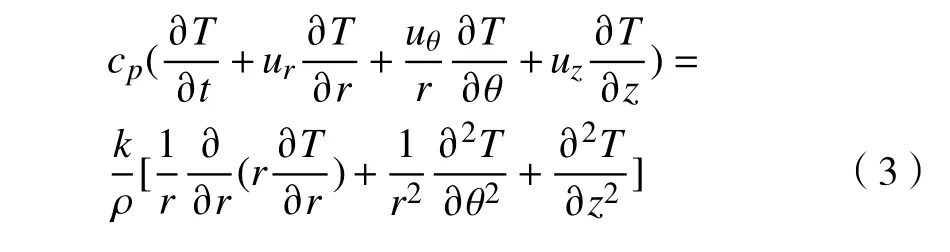
式中:u为 速度;p为压力;T为温度; ρ0为密度;cp为 定压比热;v为运动黏度;k为导热系数;f为体积力; β为流体体积膨胀系数[10],下标r、θ、z分别表示径向、周向和轴向;ρ0为初始密度;T0为初始温度;g为当地重力加速度。
由于温度场的存在,采用Boussinesq 近似[11],将密度定义为温度的函数 ρ =ρ0(1-βVT),其中V为内、外圆筒间的体积。
1.3 模型计算设置
环隙内流动介质选用甲基硅油。内圆筒转速的提高是泰勒涡形成的主要因素,内圆筒转速以雷诺数Re=R1ωδ/v。 本文Re 取值介于20~150之间,内、外圆筒壁温差ΔT= 80 K。采用三维不可压缩层流非稳态模型求解,开启能量方程,内、外圆筒壁面设为恒温、无滑移壁面。采用PISO 算法[12]进行压力-流动耦合,残差收敛判据设置为10-5。为了获得稳定的残差收敛图,迭代时间步长[13]依次设置为0.1、0.001、0.000 01。为了加快收敛速度计算初期采用较大时间步长0.1,在流动和迭代稳定后,减小时间步长以获得稳定精确解。
2 模拟结果及分析
2.1 泰勒涡形成及演化分析
不同雷诺数下,环隙内流体在子午面流态演变如图1 所示。当Re= 20 时,流动主要处于库埃特流,即平行于筒体的层流流动状态。由于端壁效应[14],在流域上、下端部形成了“Ekman”涡[15]。随着内圆筒转速的增加,泰勒涡数量逐渐增多,最初出现于上、下端面,然后逐渐向中部发展。当Re= 105 时,泰勒涡布满了整个流域,形成稳定的层流泰勒流。此时的雷诺数为第一临界转捩雷诺数Recr1=105。随着内圆筒转速继续上升,流域内始终充满了泰勒涡。

图 1 子午面流态演变Fig. 1 Evolution of meridional flow patterns
图2 为流体在子午面周向速度分布。由图中可看出,涡核处的流速高于涡胞边缘处,且相邻两涡胞的旋转方向相反。图2 中泰勒涡流的发生及演变过程与图1 一致。当Re>130 时,流动开始从层流泰勒涡向湍流泰勒涡转变[16],第二临界转捩雷诺数约为Recr2= 130。Recr2/Recr1= 1.24,与此前研究泰勒涡流的Cole等[10]关于第二临界转捩雷诺数约为第一临界转捩雷诺数1.2 倍的结论相吻合,这也验证了模拟结果的准确性。
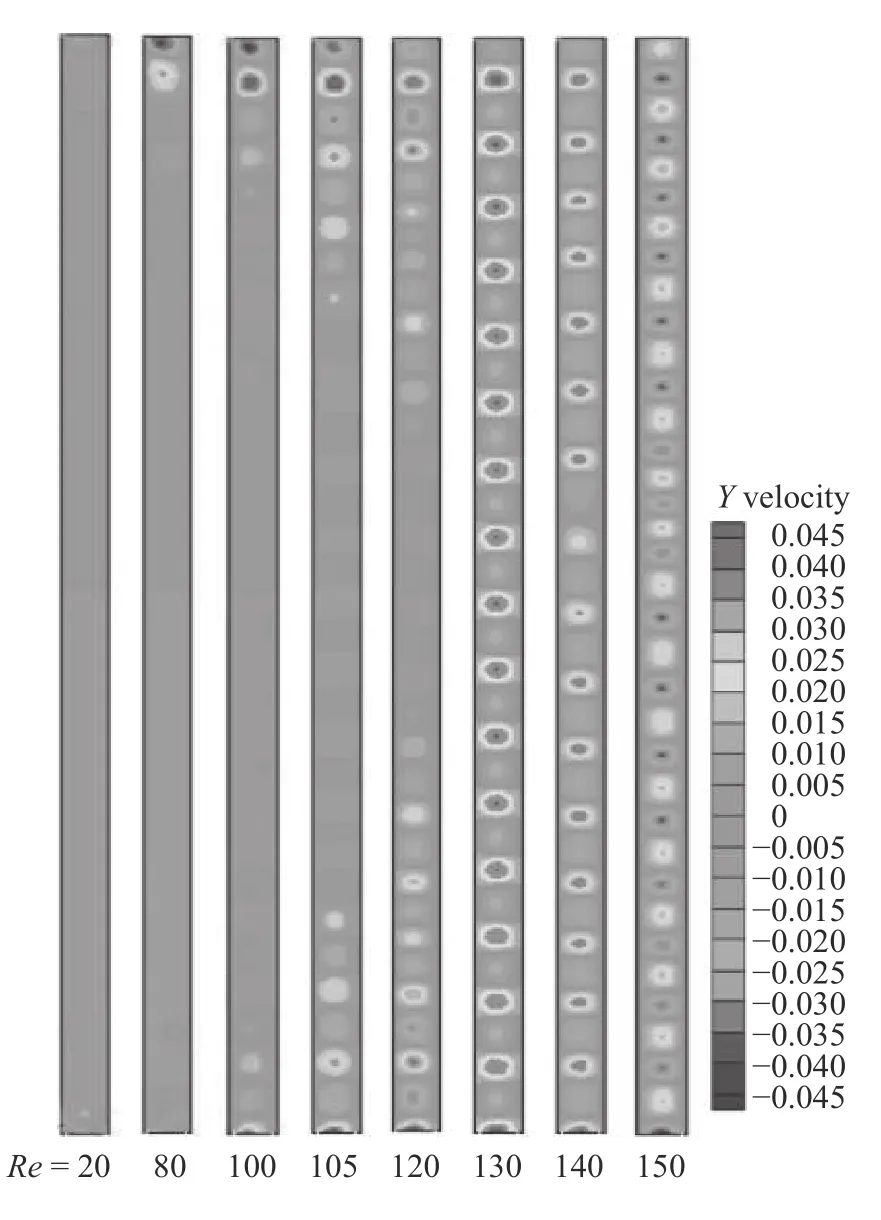
图 2 子午面周向速度分布Fig. 2 Circumferential velocity distribution in meridian plane
2.2 涡量变化分析
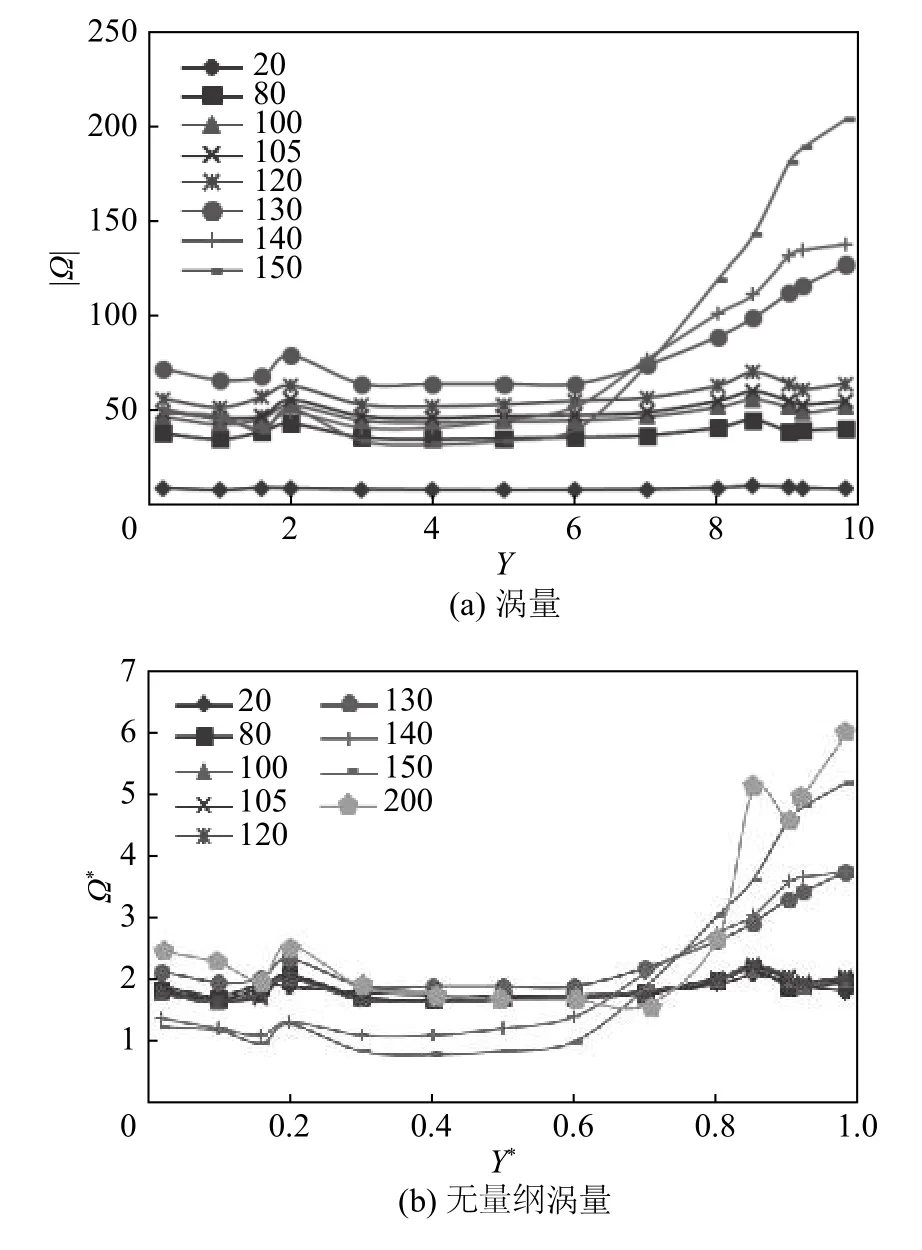
图 3 轴向z = 150 涡量和无量纲涡量Fig. 3 Axial vorticity and dimensionless vorticity at z=150 mm
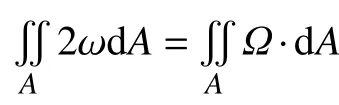
2.3 强化传热分析
图4 为轴向z=4 、150 mm 处的无量纲温度径向分布。该两截面分别位于近端面和半轴高度处,分别为最早和最晚出现涡胞的位置,最具有代表性。无量纲温度定义为T*=(T-T1)/(T2-T1)。小雷诺数下,温度分布呈现由内圆筒壁面向外圆筒壁面线性下降趋势[19],这与小雷诺数下库埃特层流流态相对应。随着雷诺数的增大,无量纲温度分布呈现内、外圆筒近壁面边界层附近温度梯度大而环隙内部温度梯度小的现象,这主要是由于泰勒涡胞的形成及强化传热效果所导致。对比图4(a)、(b)发现,相同Re下轴向z=4 mm平面的平均无量纲温度基本都高于轴向z=150 mm平面,其原因是由于近端面处的泰勒涡胞比中轴处形成得更早,强度更强,对不同温度流体的混合能力也更强,从而使得环隙内流体工质的平均温度更高。由此可知,泰勒涡柱的生成强化了环隙内部流体的传热能力。
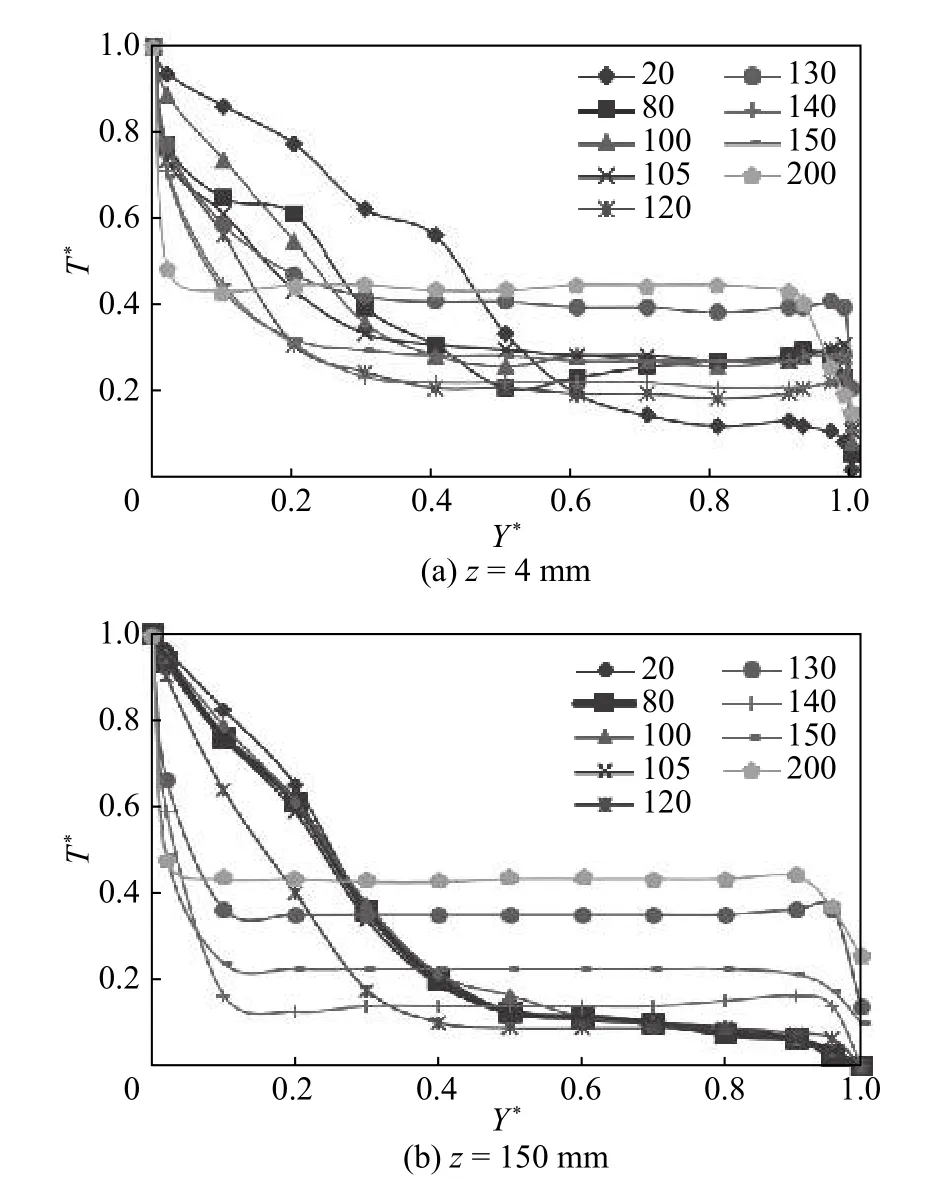
图 4 z=4、150mm 无量纲温度径向分布Fig. 4 Radial distribution of dimensionless temperature at z=4 and 150 mm
图4(a)、(b)中共同表现为,当Re<130时,总体温度均匀升高且温度稳定段逐渐变宽;当Recr2= 130 时,近端面处和中轴处总体温度和平均温度均达到最高,温度梯度主要集中在内、外圆筒壁面附近;当Re= 140 时,总体温度降低明显,当Re= 150 时总体温度又开始升高。结合图1、3(a)的结论可知,随着雷诺数的增大,泰勒涡柱随着涡量的增大而形成并强化,Recr2= 130 时为层流泰勒涡流态向湍流泰勒涡流态的转折点,此时也为泰勒涡柱涡量最大且最稳定的状态。因此,层流泰勒涡状态下,当Recr2=130 时,流体的传热效率最高。当雷诺数继续增大时,刚进入湍流态的泰勒涡柱边界出现波动,流体微团由有序流动变为无序波动,导致强化传热效率降低,并低于层流泰勒涡流态下的稳定态(Recr2= 130),但之后随着湍动度的增加,传热效率和总体温度增大。
图5 为对应于前文中不同雷诺数条件下固定外筒内壁面处的Nu和对流换热系数h的变化趋势,由于对流换热系数较大而不容易表示,故将对流换热系数开平方根作为图例进行对比分析。由图中可以明显观察到,当Re<80 时,端壁效应占主导作用,没有泰勒涡胞的生成内壁面处的Nu变化量很小;当Re>80 时,随着Re增加,泰勒涡胞自上、下端面处产生并逐渐向轴向中线发展,可以明显地观察到Nu有升高趋势。与此同时,随着泰勒涡胞涡强度的强化和波动,其外筒内表面的对流换热强度也出现了相应的波动,但由于泰勒涡胞生成和发展总体Nu和对流换热系数h处于上升趋势,证明泰勒涡胞具有明显强化传热的能力。
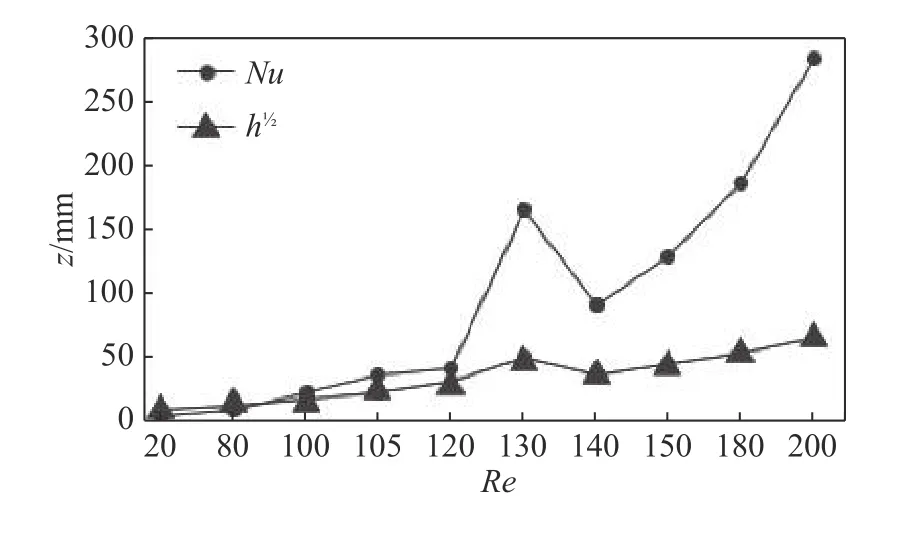
图 5 不同 Re 下总体Nu 和对流换热系数的变化Fig. 5 Overall Nu and convective heat transfer coefficients under different Re numbers
3 结 语
本文数值模拟了长径比Γ= 30 的模型内泰勒涡流流动形态演变规律,并对泰勒涡流强化传热特性进行分析。主要结论为:
(1)随着内圆筒转速的增加,由于端面“Ekman”涡的影响,涡流自两端开始形成并向流域中部发展,到达Recr1后涡流充满整个环隙并继续发展。流动从库埃特层流发展至层流泰勒涡流,并在Re>130 时向湍流泰勒涡流流型发展。涡流演变的特征数值与前人得出的实验结果相同,验证了模拟结果的准确性。
(2)当Re≥130 时,涡量出现自内圆筒壁面向外圆筒壁面方向的径向迁移,内圆筒壁面附近涡量下降较多,且不能维持涡柱的稳定,开始进入湍流泰勒涡流态,故Recr2= 130 为流动从层流泰勒涡流向湍流泰勒涡流的转折点,也是泰勒涡柱最稳定的流态点。
(3)随着雷诺数的增大,环隙内呈现内、外圆筒近壁面边界层处温度梯度大,而环隙内部温度梯度小的现象,且总体温度升高。泰勒涡的存在强化了环隙内不同温度梯度流体的径向混合,从而使得流域内温度分布更加均匀。流域内平均温度随着涡柱涡量的增大而升高,与库埃特层流环隙内线形温度相比,泰勒涡流强化传热效果显著。
(4)在层流泰勒涡及小湍动度的湍流泰勒涡流态中,当达到第二临界转捩雷诺数(本文中为Recr2= 130)时,泰勒涡柱强化传热效率最高。
