竖直提升管内气泡运动状态数值模拟研究
2020-12-18郝淑萍刘道平
郝淑萍,刘道平,杨 亮
(上海理工大学 能源与动力工程学院,上海 200093)
气泡泵是为整个单压吸收式Einstein 制冷循环系统提供动力的核心部件。其主要性能评价参数为最大提升高度和液体提升率。而与其性能相关的主要因素有结构形式、运行参数和工质对[1]。气泡泵本质上是一段具有加热功能的提升管(如图1 所示),目的是通过加热其底部以产生上升的气液两相流来泵送液体。
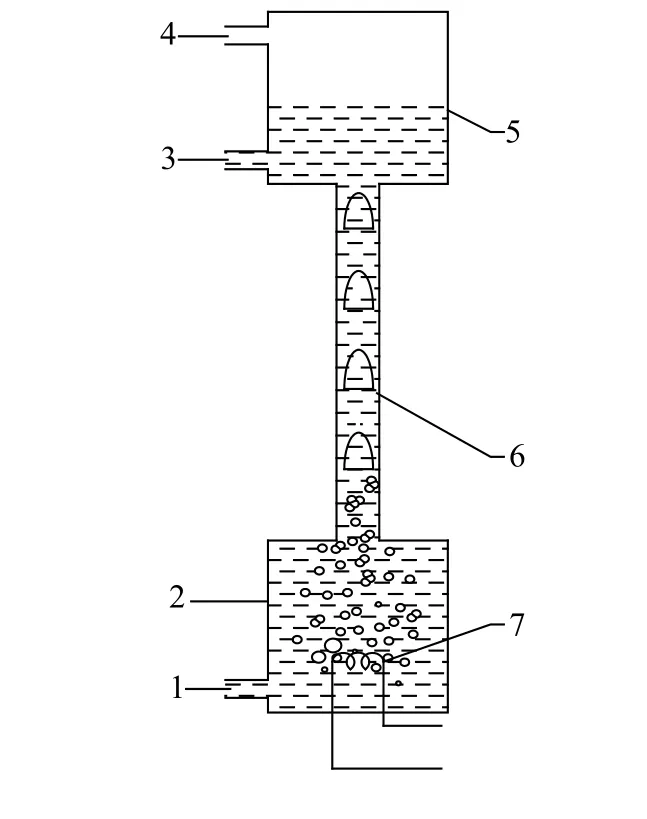
图 1 单压吸收式Einstein 制冷循环气泡泵简化模型Fig. 1 Simplified model of bubble pump in singlepressure absorption Einstein refrigeration cycle
1998 年Delano[2]在Stenning 和Martin 的空气提升泵理论[3]的基础上设计了一个气泡泵,依据质量守恒和动量守恒定律建立了气泡泵的数学模型,并分析了加热功率、提升管直径、浸没比对气泡泵性能的影响[2]。阙雄才等[4]针对无泵溴化锂吸收式太阳能制冷机中的气泡泵建立了绝热弹状流气泡泵的数学模型。薛相美等[5]根据两相流流型转换理论,推导出气泡泵从弹状流向泡状流转变和从弹状流向块状流转变时液体流量、气体流量与管径的关系式,并根据空气提升理论、能量平衡、质量平衡推导出气泡泵的性能关系式。平亚琴等[6-7]以两相流分相模型理论为基础,以水为工质,建立了气泡泵在绝热弹状流工况下工作特性的理论模型,并通过实验论证了该理论模型的有效性。Chan 等[8]还基于气泡泵自身的提升特点,在Praff 模型的基础上考虑热量损失和空隙率增加的因素,提出了一个新的气泡泵理论模型,并在大气压下以水为工质进行实验验证。陈永军等[9-11]提出了一种新型的连续变截面管(内径从 11 mm 渐变至8 mm)渐缩式气泡泵装置,并对其提升性能进行了实验分析。李华山等[12]使用有机工质研究了提升管管径对气泡泵性能的影响规律。高洪涛等[13-14]搭建了两级气泡泵与溴化锂制冷系统耦合特性实验台,并以改进后的格子玻尔兹曼自由能模型研究了单个气泡上升和双气泡融合过程,分析了气泡泵性能及气泡温度变化。
目前学者对气泡泵的研究主要集中在加热功率、竖直提升管管径和管数对气泡泵性能的影响。本文通过对竖直上升管内分别为纯水和氨水时的气液两相流动、气泡成型及运动进行数值模拟,观察其形成、运动规律,得出压力、热源温度等参数对气泡泵性能的影响。模拟结果对气泡泵的结构设计和系统参数的选取有参考价值。
1 数值模型
1.1 计算模型及边界条件
基于所搭建的单压吸收式Einstein 制冷循环气泡泵实验台,对本文研究的气泡泵作出如下假设:①储液器中液位高度保持不变;②气泡泵提升管中保持稳定的一维流动;③气泡泵的驱动压头等于气泡泵的压力损失。经分析,垂直提升管内气液两相流的各流型间存在明显的分界面,同时根据多相流模型的选择原则以及简化的模拟条件,针对本文所研究的问题选定VOF(流体体积函数)模型进行模拟计算。
图2 为竖直提升管简化计算模型。竖直提升管管径为10 mm,两相流质量流量为0.282 g·s-1,数值模型网格单元数为75 000,其中提升管底部为热边界,顶部为压力出口边界,两侧为固定绝热壁面边界。
1.2 控制方程
(l)质量守恒方程
流场中任意状态的改变都必须满足质量守恒定律,即
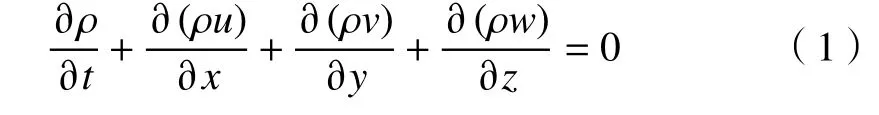
式中:ρ为密度;t为时间;u、v、w分别为速

图 2 竖直提升管的简化计算模型Fig. 2 Simplified calculation model of the vertical riser
度在x、y、z方向的分量。
(2)动量守恒方程
流体运动除了要满足质量守恒定律之外,还要满足动量守恒定律。由动量守恒定律可推导出x、y和z三个方向的动量守恒方程,即
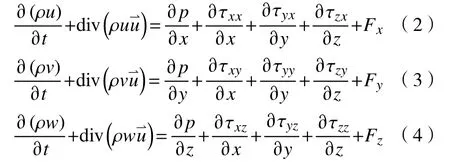
式中:p为作用于流体微元上的压强;为流体微元矢量速度;τxx、τxy、τxz、τyy、τzz、τyz、τzx、τzy、τxz分别为因分子黏性作用产生的作用在微元体表面上的黏性应力τ的分量;Fx、Fy、Fz分别为三个方向的单位质量力。
(3)能量守恒方程
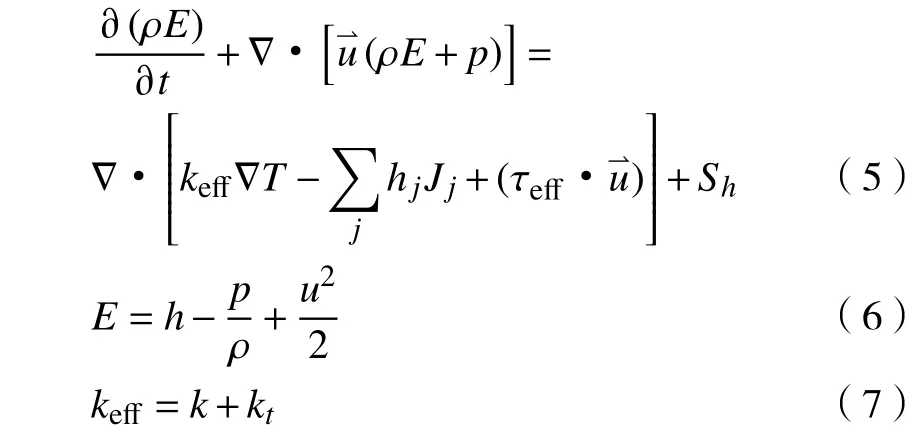
本文中在对气泡泵中气泡形成及运动进行模拟时涉及热交换,所以在满足上述两个定律的基础上还应满足能量守恒定律,即式中:E为流体微团的总能,为内能、动能和势能之和;h为焓;hj为组分j的焓;keff为有效热传导系数;kt为湍流导热系数,其值根据所用的湍流模型确定;Jj为j组分的扩散通量;Sh为包括了化学反应热及其他用户定义的体积源项;τeff为有效剪应力;T为微元体温度。
2 竖直提升管数值模拟计算及结果分析
分别以纯水、质量分数为18%的氨水为工质,选取过热度分别为20、40 K,压力分别为0.1、0.2、0.3、0.4 和0.5 MPa 的工况,对气泡泵竖直提升管内气泡的形成及运动进行数值模拟。
2.1 以纯水为工质
以纯水为工质时所需的饱和水和饱和水蒸气的热物性参数[15]如表1 所示。数值模拟得到的气泡形成及运动图像如图3 所示。
由图3 中可以看出,当系统过热度一定时,随着压力增加,管内气泡随机生成且分布不均,其生成时间逐渐延长,而且气泡数量变少,单个气泡直径也减小,但是气泡相对运动变缓慢,所以气泡密度和分布均匀性增加。这是因为随着压力和水的饱和温度增加,水的物性参数发生了变化,液体密度相对减小,气体密度相对增加,比热容相对增加,黏度和表面张力减小。这些都对气泡形成产生了一定的影响。而由图3(a)、(f)中可看出,当压力一定时,随着过热度增加,形成气泡的时间明显变短,气泡凝聚的体积变大,所以过热度较高时易于形成弹状流。
2.2 以氨水为工质
当Einstein 制冷循环工作压力为0.4 MPa时,根据经验方程及拟合方程[16-23]计算的质量分数为18%的氨水的物性参数如表2 所示。
当压力为0.4 MPa 时,选取过热度分别为20、40 K,对竖直提升管内工质为质量分数为18%的氨水的气液两相流动进行了模拟,得到的竖直提升管中气泡形成及运动图像如图4 所示。由图4 中可以看出,在压力一定时,随着过热度增加,气泡随机生成,形成气泡的时间变短且脱离壁面的速度加快,气泡的融合体积增大;在过热度较大的工况下,气泡分布均匀性增加,易于形成弹状流。将图4 与图3(d)、(i)对比可知,相对于以纯水为工质的工况,以氨水为工质时气泡形成的速度更快,但相对气泡直径较小,且气泡形状较不规则。这是因为氨水和水的物性差异,且氨水的表面张力较小的缘故。该模拟结果对Einstein 制冷循环系统中气泡泵参数的设计选择提供了参考:即相对于0.4 MPa的系统压力,需采取较高的热源温度才能保证气泡泵的正
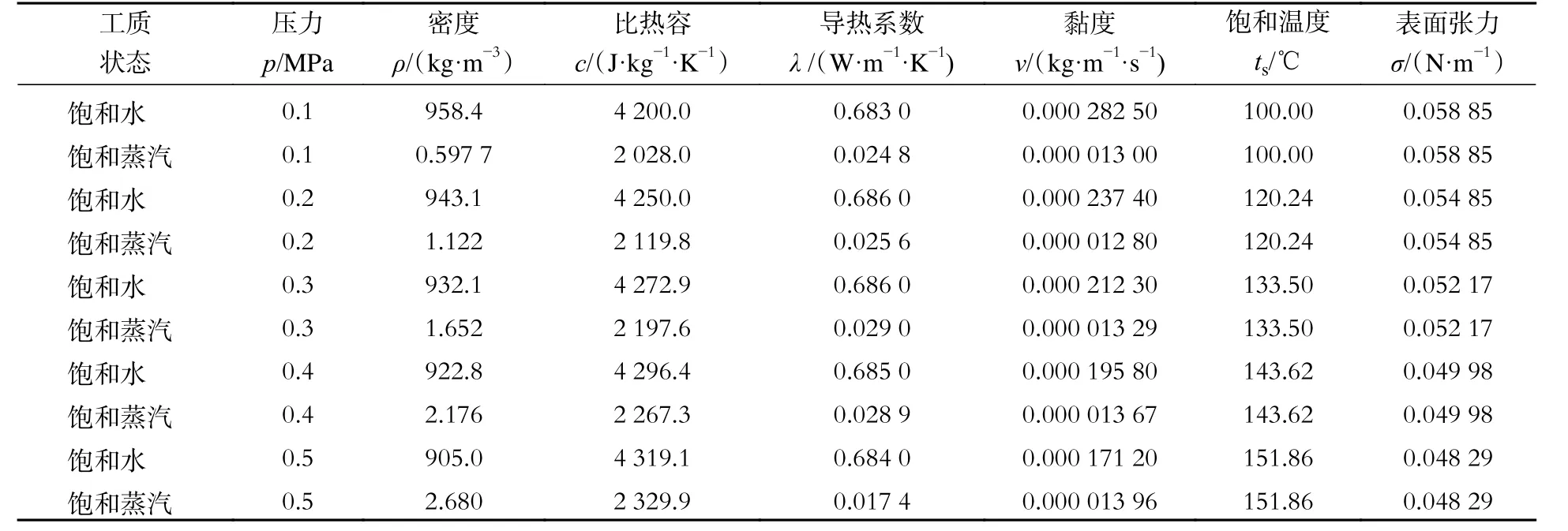
表 1 饱和水和饱和蒸汽的热物性参数Tab. 1 Thermophysical parameters of saturated water and saturated steam

图 3 过热度分别为20、40 K 时不同压力下气泡形成及运动图像Fig. 3 Bubble formation and motion under different pressures at the degree of superheat =20 and 40K

表 2 压力为0.4MPa 时质量分数为18%的氨水的物性参数Tab. 2 Thermophysical parameters of the ammonia with mass fraction of 18% at 0.4 MPa
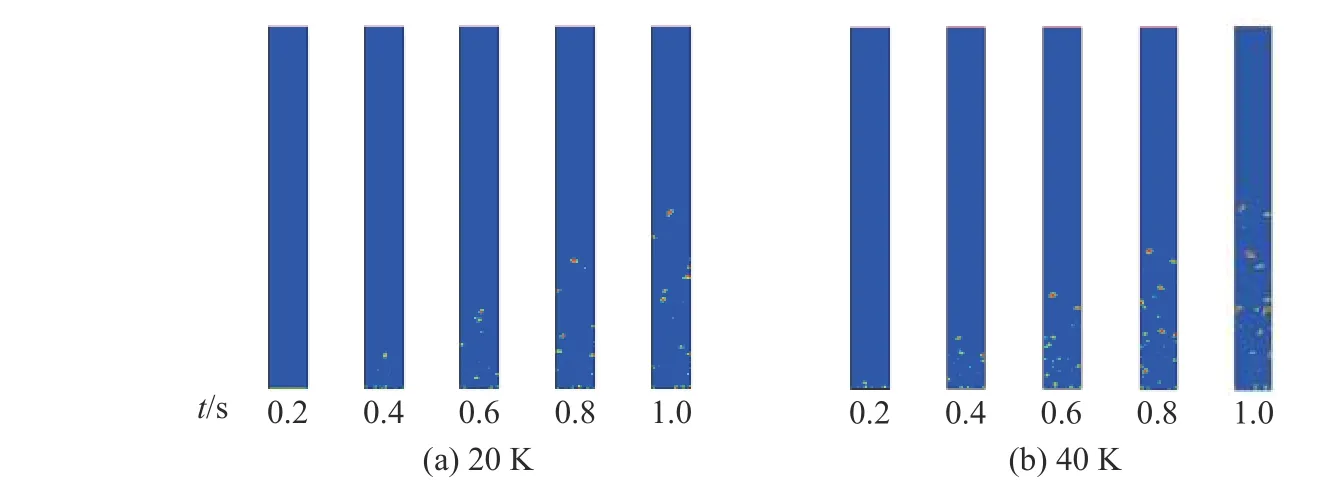
图 4 竖直提升管在压力为0.4 MPa 时不同过热度下的模拟结果Fig. 4 Simulation results of the vertical riser under different superheat at 0.4 MPa
3 结 论
本文建立了竖直提升管的简化模型,利用拟合公式计算了纯水和氨水的一系列物性参数,并分别以纯水和质量分数为18%的氨水为工质,对气泡泵竖直提升管内气泡形成及运动进行了数值模拟。研究结果发现:
(1)在过热度恒定时,单个气泡的生成时间随着压力增加而延长,且气泡体积变小,但气泡均匀性增强;当压力恒定时,气泡生成速率随着过热度增大而加快,且融合体积也增大,易于形成系统所需弹状流。
(2)压力为0.4 MPa 时,需采取较高的过热度才能保证气泡泵的正常运转,而实际上气泡泵内氨水浓度会有所波动,相关计算数据的精确性和所拟合的性能曲线的严谨性均有待进一步考察,也可根据管内两相流变化规律分段细化探究。
