透过现象看本质：由2461问题引发的探究

张为康 吴思怀

(南京师范大学数学科学学院 210023)

《数学通报》2461问题是一个三角函数求和问题,它本质上是一个数论问题,本文将从初等数论的角度提出一般化的定理并给出详细证明.

1 原命题概述

2 问题一般化

作者这样的构造方法很巧妙,往往很难想到,但从其本质来看就会觉得很自然.

观察解题过程中x,y的构造，很容易联想到单位根的有限和,即高斯和的相关内容.代数式中π 前面的系数1,3,4,9,10,12为mod13的二次剩余，2,5,6,7,8,11为mod13的二次非剩余，而在数论中，二次剩余与二次非剩余联系紧密，所以构造y与x进行配对计算，在数论中是自然而然的想法.原问题中13作为一个素数，不失一般性，而在二次剩余内容中，4n+1型素数与4n+3型素数的性质又有本质上的差别.

综合以上考虑，将原问题进行一般化的推广，得到以下定理.

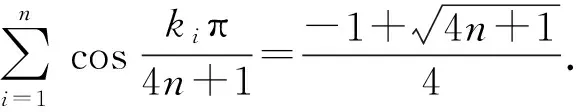
3 证明定理

为了证明这一定理,先给出初等数论中的一些基本定义和引理.

定义1设素数p>2,d是整数,p|d.如果同余方程x2≡d(modp)有解,则称d是模p的二次剩余;若无解,则称d是模p的二次非剩余.

引理2设素数p>2,p|d1,p|d2,那么,

(1)若d1,d2均为模p的二次剩余,则d1d2也是模p的二次剩余;

(2)若d1,d2均为模p的二次非剩余,则d1d2也是模p的二次剩余;

(3)若d1是模p的二次剩余,d2是模p的二次非剩余,则d1d2是模p的二次非剩余.

引理3-1是模p的二次剩余的充要条件是p≡1(mod4).

下面对此定理进行严格的论证.

证明因{1,2,…,4n}是模p的一个既约剩余系,由引理1不妨设M={s1,s2,…,s2n}是{1,2,…,4n}中的所有模p二次剩余的集合,设N={t1,t2,…,t2n}是{1,2,…,4n}中的所有模p二次非剩余的集合.令

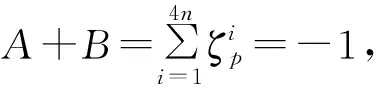
由引理2,对∀c∈{1,2,…,4n},

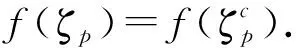
于是得到4n个等式

将这4n个式子左右两边相加,得

=-(a1+a2+…+a4n),

又a1+a2+…a4n=4n2,则AB=f(ζp)=-n.

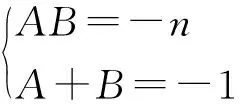
A,B是方程x2+x-n=0的两根.

实部相等可得,

由引理3, -1是模p的二次剩余,于是4n+1-si(i=1,2,…,2n)也是模p的二次剩余,且si≠4n+1-si,即si与4n+1-si在集合M中成对出现.不妨设si+n=4n+1-si(1≤i≤n),由抽屉原理知min{si,4n+1-si}≤2n.令ki=2min{si,4n+1-si}(1≤i≤4n),则1≤ki≤4n,且

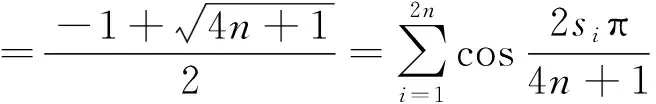
这样就找到了n个符合条件的数,定理得证.

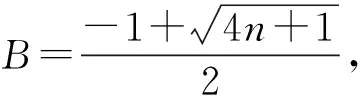
4 推论与推广

由上面的证明过程,还可以得到以下推论.

推广当p是4n+3型素数,∃1≤h1≤h2≤…≤hn≤4n+2,使得

其中hi∈Z(i=1,2,…,2n+1).

5 回顾与反思

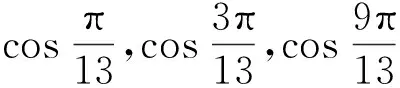
由于2,5,6为模13意义下的二次非剩余,利用推论知

原命题得证.

《数学通报》2461问题的探究证明可以从数论中找到理论依据,有兴趣的读者可以从高斯和理论中找到更一般的推广.