基于核心素养的高中数学“四元”教学的探索与实践
2020-12-17李云杰林新建
李云杰 林新建,2
(1.福建省福清市教师进修学校 350300;2.闽南师范大学数学与统计学院 363000)
在过去的教学活动中,教师可能更关心如何教,但基于数学核心素养的教学,更多地需要关心学生如何学,需要知道学生的认知水平和认知过程.
《普通高中数学课程标准(2017年版)》指出,高中数学教学应该以发展学生数学学科核心素养为导向,创设合适的教学情境,启发学生思考,引导学生把握数学内容的本质,强调创设的情境并提出问题对于启发学生思考、发展数学学科核心素养的重要性.
一个理想的数学教学过程大概可以描述如下:创设合适的教学情境、提出合适的数学问题;启发学生思考、鼓励学生与他人交流;让学生在掌握知识技能的同时,理解数学知识的本质;感悟数学的思想、形成和发展数学核心素养.
基于此,我们提出了整合教师教和学生学的高中数学“四元”教学法:“设、启、促、导”,与“试、悟、述、用”,具体地说,就是教师从元认知的角度“设问、启思、促悱、导悟”,引领学生“试答、体悟、述评、致用”.这是基于核心素养的教学,是元认知理论在数学教学中的有益尝试.
下面以一道高考试题为例,就高中数学“四元”教学的设计与应用作一探析.


1 教师设问、学生试答
教学的设计与实施,要特别重视情境与问题,因为核心素养是在特定情境中表现出来的知识、能力和态度,在不同情境中解决问题的能力直接影响学生数学素养的形成和发展,情境与问题搭建了学生数学核心素养发展的桥梁.
教师要努力创设合适的教学情境,提出合适的数学问题,让学生探索尝试,积极地参与到数学教学过程,这是培养和发展数学核心素养的重要途径和渠道.
基于学生对向量问题的认知特点,向量加减的三角形和平行四边形运算法则应成为我们解题的首选方法,教师应先设计利于向量加减运算的教学情境,通过以下问题引领学生运用“基底法”求解问题.
问题1:本题是向量问题,解决向量问题的首选方法是什么?
问题2:运用“基底法”解决向量问题的关键是什么?
问题3:如何基于图形特征选择合适的“基底”?如何将未知向量更好地转化为基底以求解?
通过上述问题,学生充分经历问题的感知、表征、结构分析、寻找策略、形成计划、实施计划等认知活动和反思总结等元认知活动,尝试着选取合适的向量作为基底,将其他向量用基底表示予以作答.
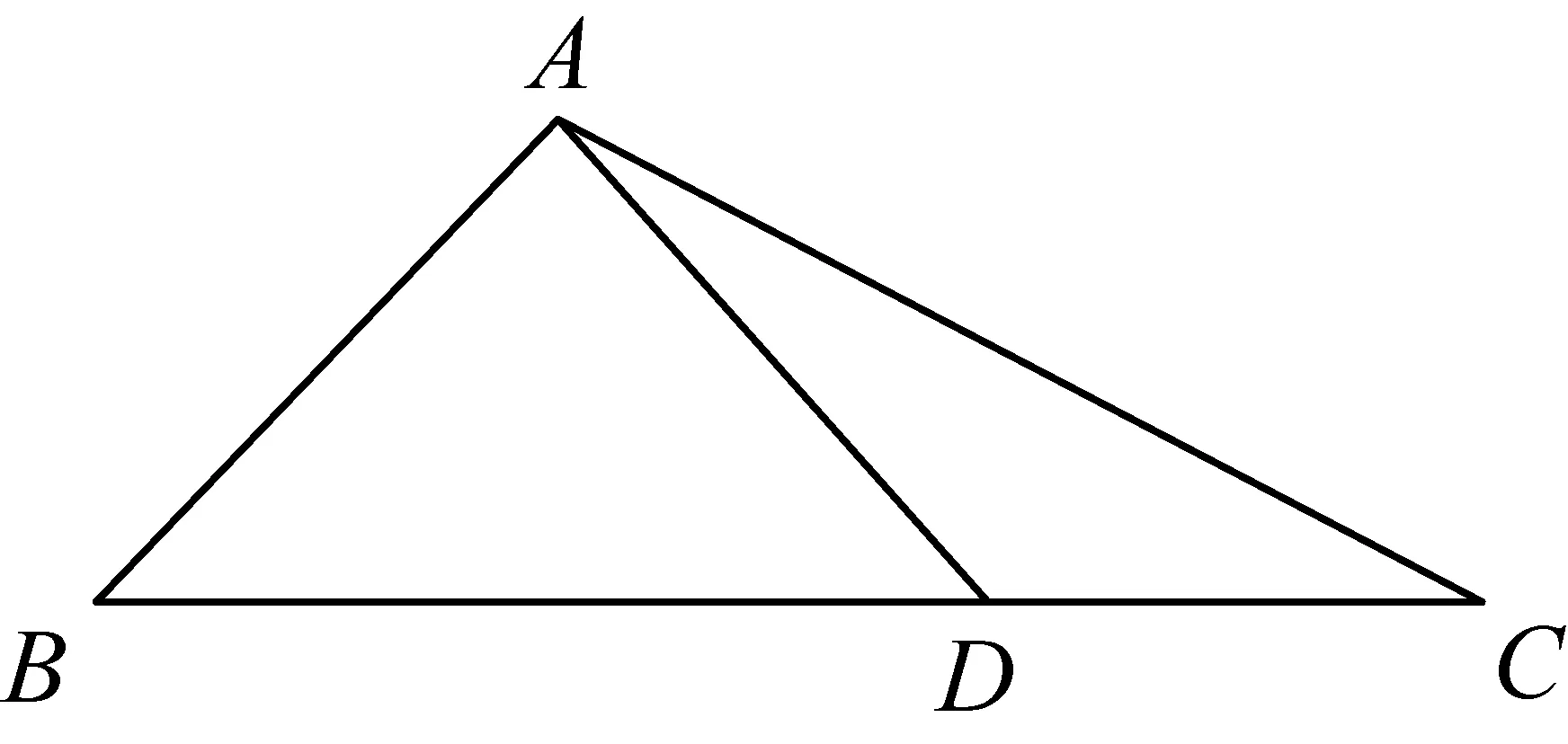


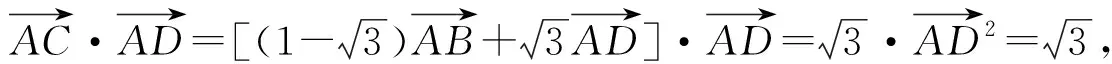
评析:一个情境是否合适并不取决于情境本身,而在于所提出的问题能否揭示数学的本质.在数学教学中,教师要提出适合学生研究的问题,创设合适的教学情境,让学生尝试探索,提高思维的灵活性、发散性和广阔性,提升解决问题的境界,培养和发展数学核心素养.
2 教师启思、学生体悟
核心素养的培养侧重学生的自主探究和自我体验,更多地依靠学生自身在实践中的摸索、积累和体悟,教师要善于启迪学生思考,鼓励学生积极交流.
教师应根据学生的认知水平,引领学生从题目所涉及的基本概念上寻找思路,学生认知的最近发展区是学生的知识生长点,也是数学解题教学的基准点,从这里出发启迪学生思考,容易让学生理解领悟.
启思1:基于学生对向量数量积的定义认知,教师可启迪学生联想“数量积”的几何意义:一个向量与另一个向量在这个向量上的投影的乘积,鼓励他们体悟运用“定义法”予以求解.
由此,可过点D作AC的垂线,或过点C作AD的垂线.
如图,过点D作AC的垂线,垂足为H,
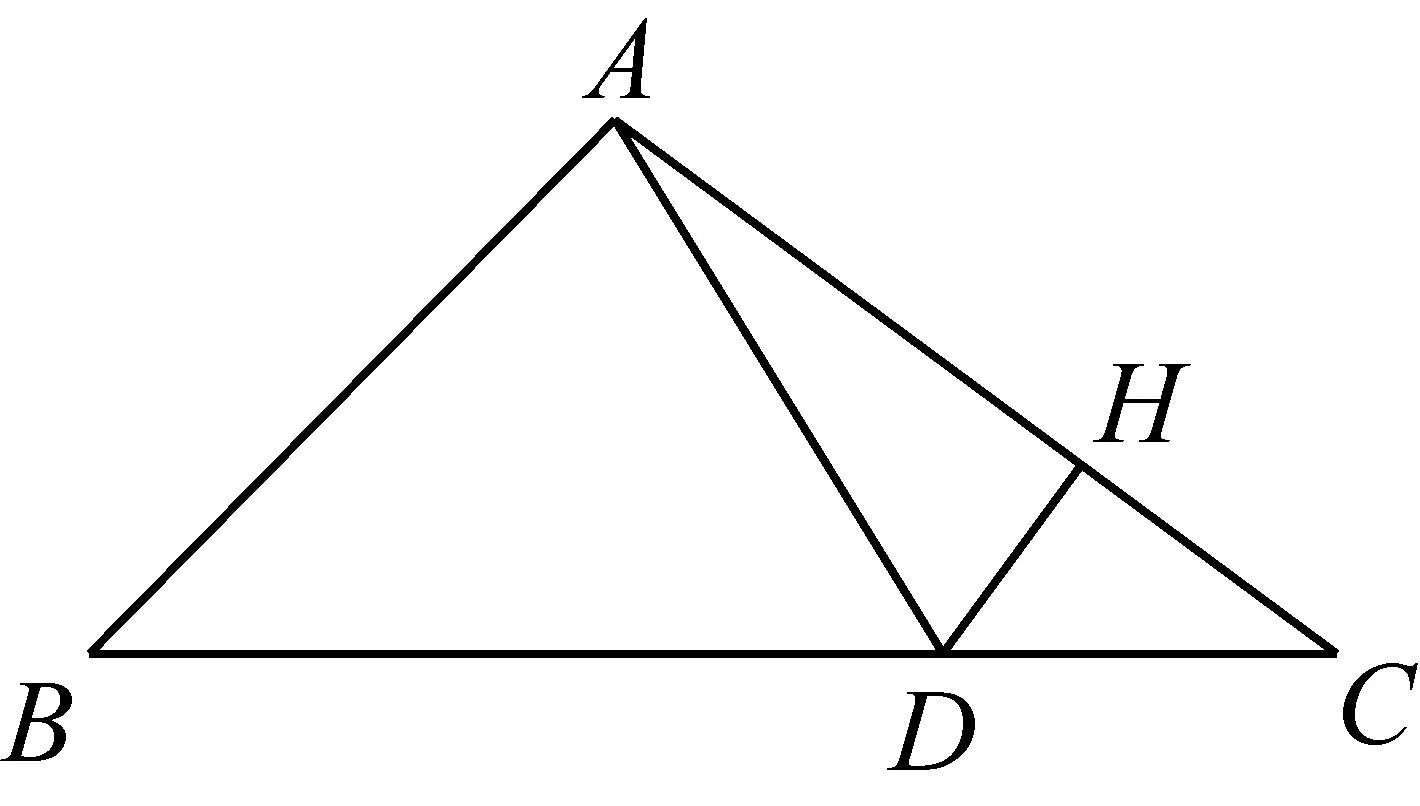

于是转换视角,过点C作AD的垂线.
如下图,过点C作AD的垂线,垂足为H,
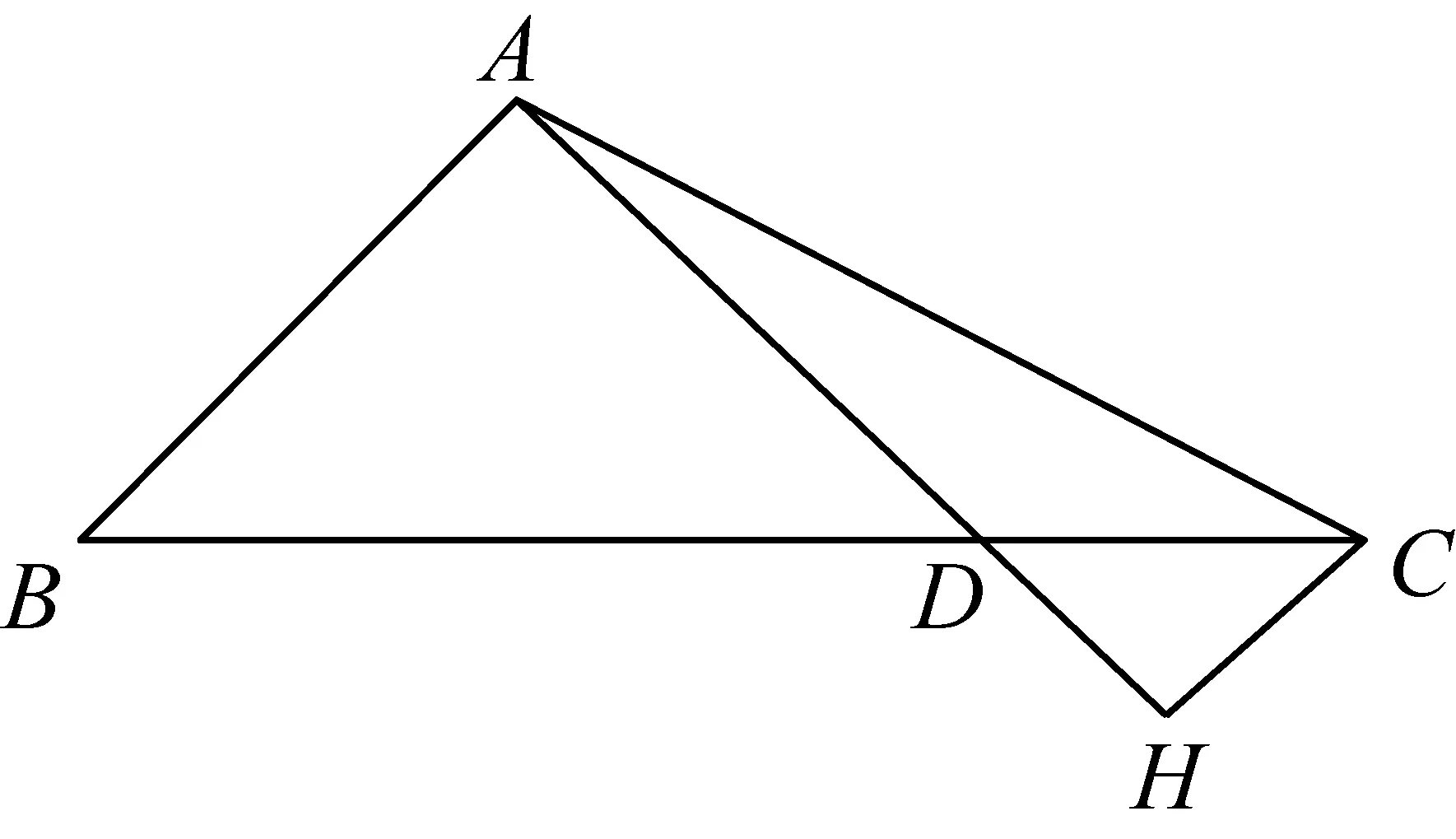
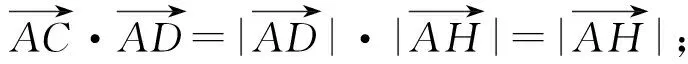
容易判断△BAD∽△CHD,从而有


启思2:基于学生对向量数量积的公式认知,教师也应启迪学生联想“数量积”的公式——a·b=|a|·|b|·cos


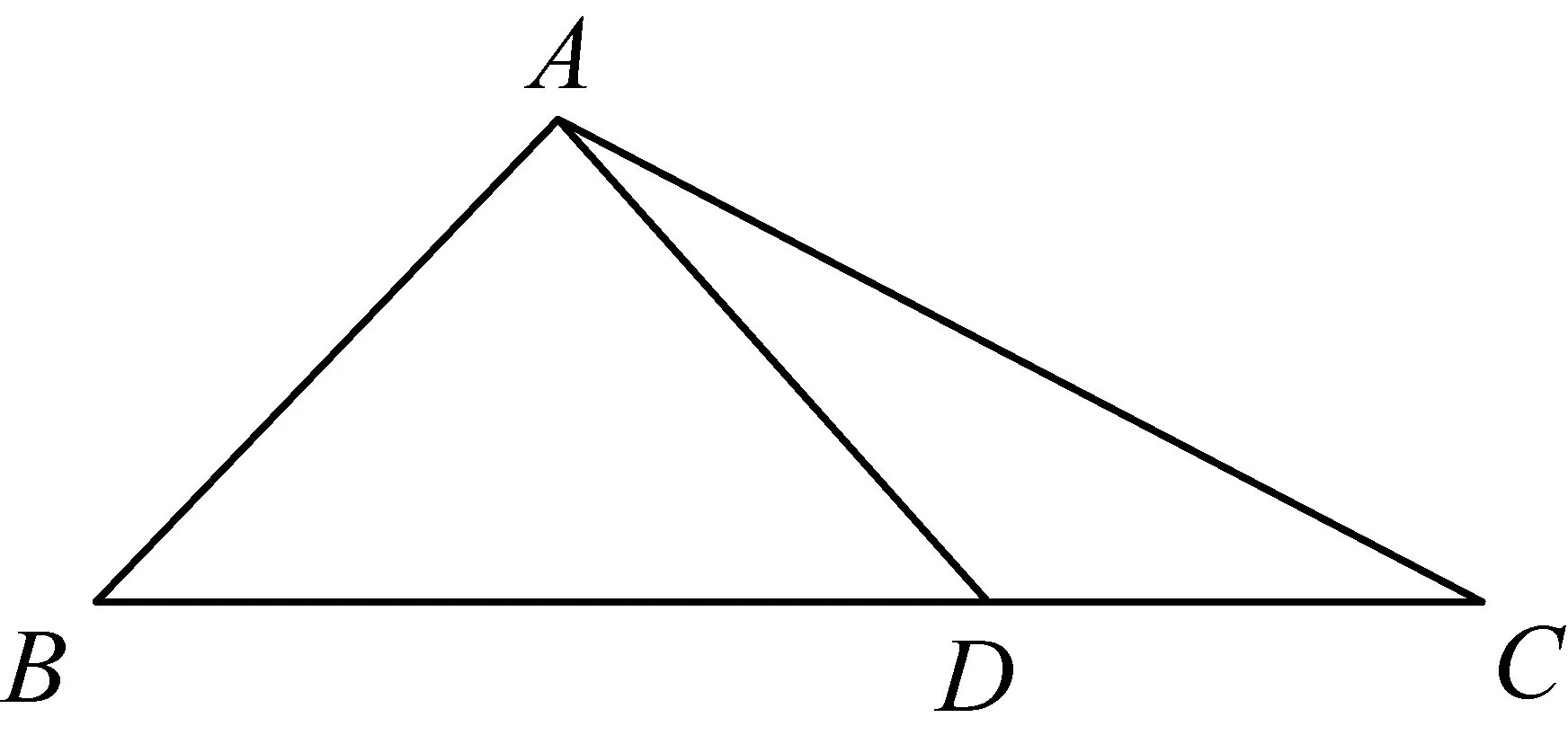
在△ABC中,由正弦定理可得
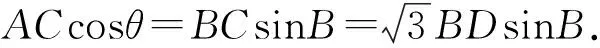
而在Rt△ABD中,BD·sinB=AD=1,

评析:虽然教无定法,但是教学必须有原则,这个原则就是以学生的发展为本.更具体地说,就是要遵循学生的认知特点,启迪学生思考,鼓励学生交流,并从探究交流中体悟,真正学会学习.
3 教师促悱、学生述评
在教学中,教师应当结合教学任务及其蕴含的数学核心素养促悱,引导学生用数学的眼光观察现象、发现问题(数学抽象);引导学生用数学的思维分析问题、解决问题(逻辑推理);引导学生用数学的语言描述背景、表达问题(数学建模).只有这样,才能在问题解决的过程中,促使学生理解数学内容的本质,培养他们的“三会”,提升学习数学的兴趣,提升数学教学的效能.
基于向量问题的“数形”特征,一些较为复杂的向量问题,一旦引入“坐标”就会变得异常简单,原因就在于“坐标”改变了学生的认知结构,把原来的几何问题转化为代数问题,使问题变得具体形象,降低了处理的难度.
所以,教师应促进学生悱发——什么是解决向量问题的最有效方法?如何基于问题的特征,合适选用坐标系以简化求解途径和运算,等等.
通过悱发,引领他们述评解答问题的思路与过程,在掌握知识技能的同时,真正理解向量知识的本质.

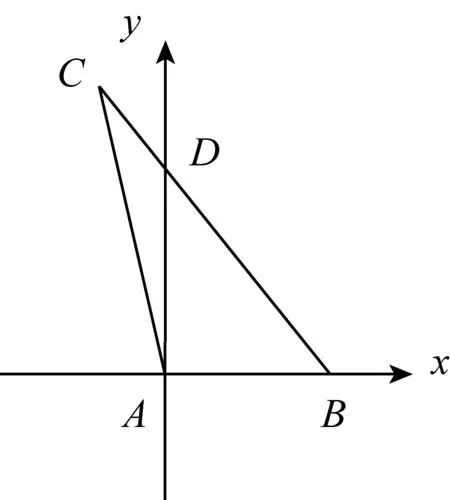



评析:对于向量问题,突出“向量法”求解的意义在于:由“形”出发,把相关的点线“向量化”,这有三种方式:用已知向量表示、用基底表示、用坐标表示,用的最多的应是坐标表示.
教学中,不同的内容(如新课、习题课、复习课)有不同的表现形式,教师应按照学生的认识规律和不同知识内容的发生发展规律设计好教学,课堂教学中愤悱促发,放手让学生述写议评,则是充分发挥主体性,提高课堂教学质量的基本保证.
4 教师导悟、学生致用
既然数学核心素养是“四基”的继承和发展,那么“四基”就是发展学生数学核心素养的有效载体,所以教学中教师应当强调“四基”,引领学生感悟知识所蕴含的数学思想,并学以致用,在应用中积累数学思维和实践的经验,形成和发展核心素养.

这给了我们启示(“特殊与一般思想”的感悟):若将AB特殊化,将动态图形固定下来,不是更方便求解吗?

在△ABC中,由余弦定理得
AC2=AB2+BC2-2AB·BC·cos∠ABC
在△ADC中,由余弦定理得
DC2=AD2+AC2-2AD·AC·cos∠DAC,
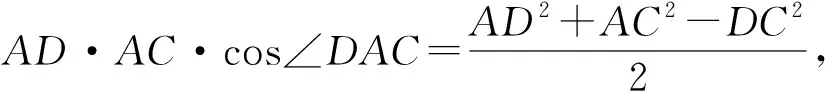

更进一步,若令AB→0,即将AB极限化,情况如何呢(“有限与无限思想”的感悟)?
这样,我们根本不用动笔,看图即得答案.

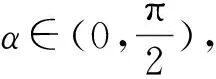



瞬间完成解答,不亦乐乎!
通过以上导悟后,教师应不失时机地引领学生学以致用,以提升他们运用数学思想解决数学问题的能力.
例1(2012年高考全国新课标卷理科16题)数列{an}满足an+1+(-1)nan=2n-1,则{an}的前60项和为________.
分析:本题是填空把关题,依常规方法求解较繁.若能感悟到本题中的数列是变化的,但结果不会因为数列的变化而变化,由此我们可将首项特殊化予以求解.
解析:由an+1+(-1)nan=2n-1,
得an+1=2n-1-(-1)nan.
令a1=1,则有a2=2,a3=1,a4=6,a5=1,a6=10,a7=1,a8=14,…
至此可以发现,数列{an}的奇数项均为1;偶数项是以2为首项,4为公差的等差数列,



其实,若能感悟到问题的一般性——k2的值随着k1的值的变化而变化,但k1k2的值是不会变化的,则可将k1的值特殊化,如令k1=1,将AB的方程y=x+2代入双曲线的方程,可轻松求得点P的坐标为(1,3),进而得到k2=3,k1k2=3,这样大大简化了运算,轻松获解.
若运用极限化方法求解则更为简单快捷.
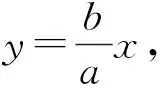
如何才能培养学生“从经验中发现规律”的能力呢?这需要引领学生感悟思想,养成“从思想的高度考察具体事例”的意识,和“透过现象看本质”的能力.
这是观念问题,是思维习惯问题,也是思想方法问题.这是一个长期的、潜移默化的过程,是逐渐养成的一种思维习惯,这个习惯日积月累就形成了数学素养.
总之,虽然影响数学课堂教学质量的因素众多,如教学环境条件、学生的学习动机和积极性、学生已有的基础等,但是,教师主导作用与学生主体作用的充分协调发挥却始终是最重要的.
为了更好地协调师生双方的主导与主体作用,在学科知识发生发展的真实过程中,需要遵循师生共同活动的原则,通过师生双方教与学积极协调的活动,展示教学内容的过程性,在知识的发生发展过程中完成认识任务,这是实现素养教学的基本要求和根本保障.
