数学问题解答

2020年9月号问题解答

(解答由问题提供人给出)

2561 已知 如图，在△ABC中，点D1、D2在BC上，且∠BAD1=∠CAD2.过点D1、D2分别作AC的平行线D1E1、D2E2，与AB分别交于点E1、E2.

(北京市朝阳区教育研究中心 蒋晓东 100028；北京市朝阳区芳草地国际学校富力分校 郭文征 100121)

证明如图，因为D2E2∥AC，

所以∠E2D2A=∠CAD2.

因为∠BAD1=∠CAD2，

所以∠BAD1=∠E2D2A.

因为D1E1∥AC，D2E2∥AC，

所以D1E1∥D2E2，所以∠AE1D1=∠AE2D2.

所以AE1·AE2=D1E1·D2E2.

①

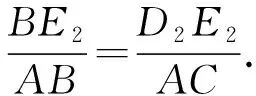
②

由①+②得

又因为AE1·AE2=D1E1·D2E2，

当且仅当∠BAC的内等角分线AD1与AD2合并为∠BAC的平分线AD时，不等式中的等号成立.

2562 设a，b，c > 0，且a+b+c=3，证明:

(河南辉县一中 贺基军 453600)

证明由a，b，c> 0得

(1+a)(1+b)=1+a+b+ab

从而得(1+a)(1+b)(1+c)

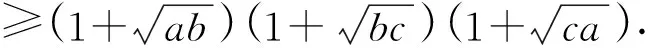
则m≥1.

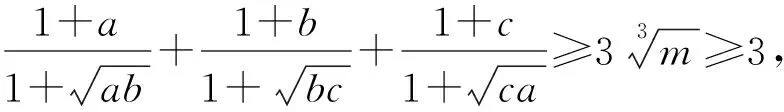
①

②

③

由① + ② + ③ 得

代入a+b+c=3 得

2563△ABC，E、F分别在AB、AC上且EF∥BC交△ABF的外接圆于D，EG∥AC交CD于G，求证：∠ABF=∠CBG

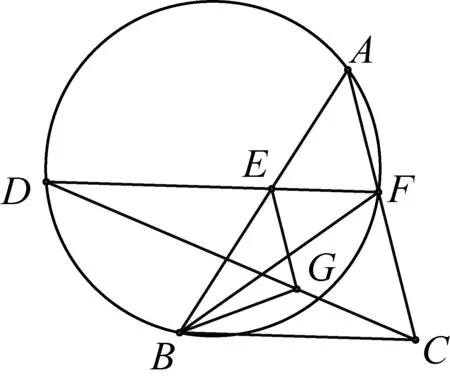
(江西师范高等专科学校 王建荣 335000)

证明连AD，延长BG分别交AC于K、交DF延长线于P，作BT∥AC交DF于T，

由∠BDF=∠BAC=∠BEG，

⟹GE·FD=FC·DE⟹BD·BE=GE·FD，

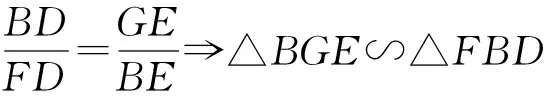
⟹∠DBF=∠EGB=∠AKB，

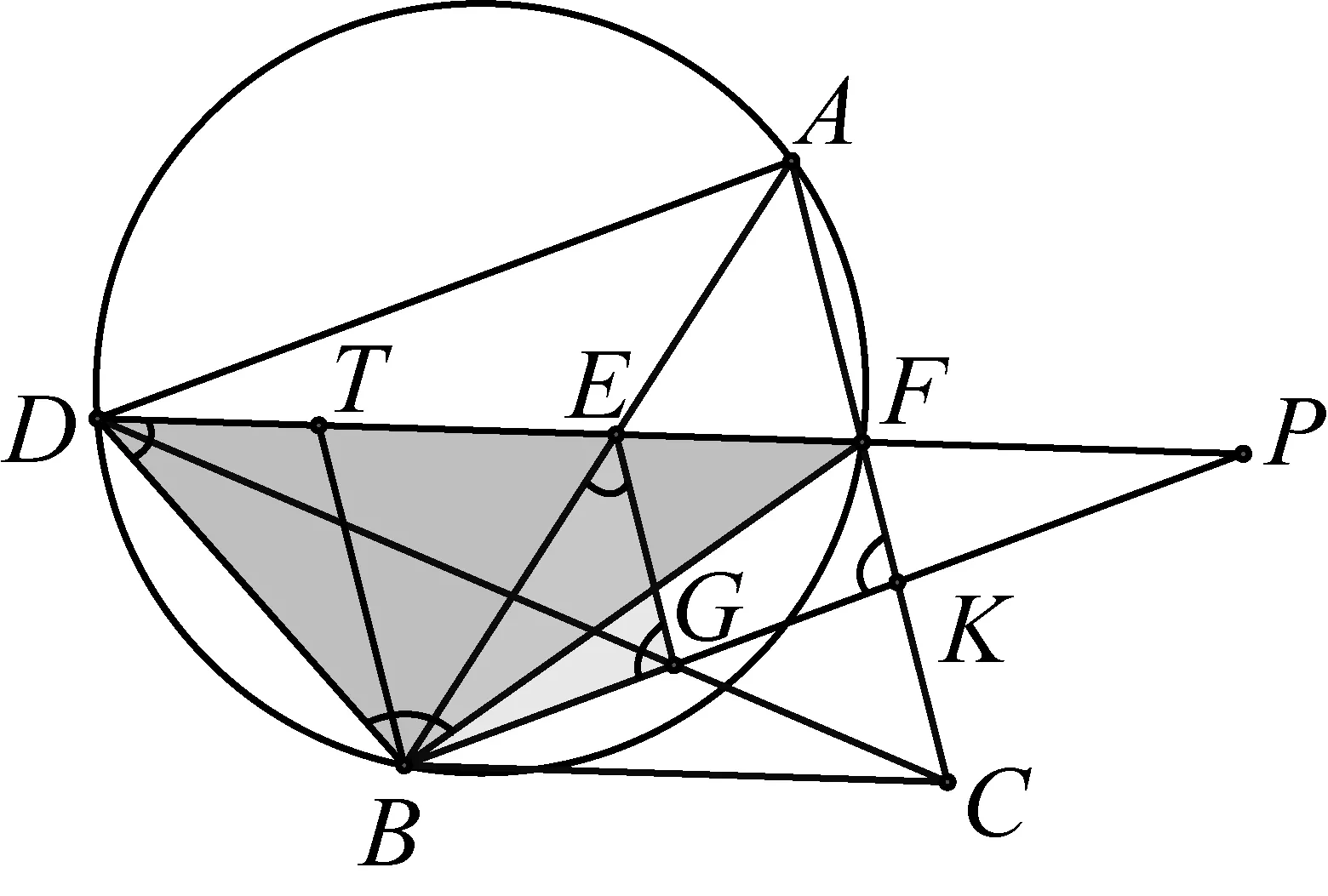
∠DBF+∠DAF=∠AKB+∠DAF=180°

⟹AD∥BK

⟹∠ABF=∠ADF=∠DPB=∠PBC.

(安徽省太和县第二小学 任迪慧 236630 )

证明由余弦定理

c2=a2+b2-2abcosC有

①

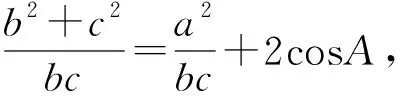
②

③

①+②+③并整理得

在△ABC中，易证

从而可得

当且仅当△ABC为正三角形时等号成立.

2565如图1，圆上依次有A1、A2、A3、A4、A5五个点，连结A1A3、A3A5、A5A2、A2A4、A4A1，得一五角星，A1A3、A2A4交于A，A1A4、A3A5交于B，若过点A1的圆的切线和A2A5的延长线交于C，则A、B、C三点共线.

(成都市金牛区蜀汉路369号2-2-35 张殿书 610036)

图1

证明设A2A5分别和A1A3、A1A4交于D、E，连结A1A2、A1A5.

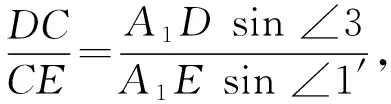
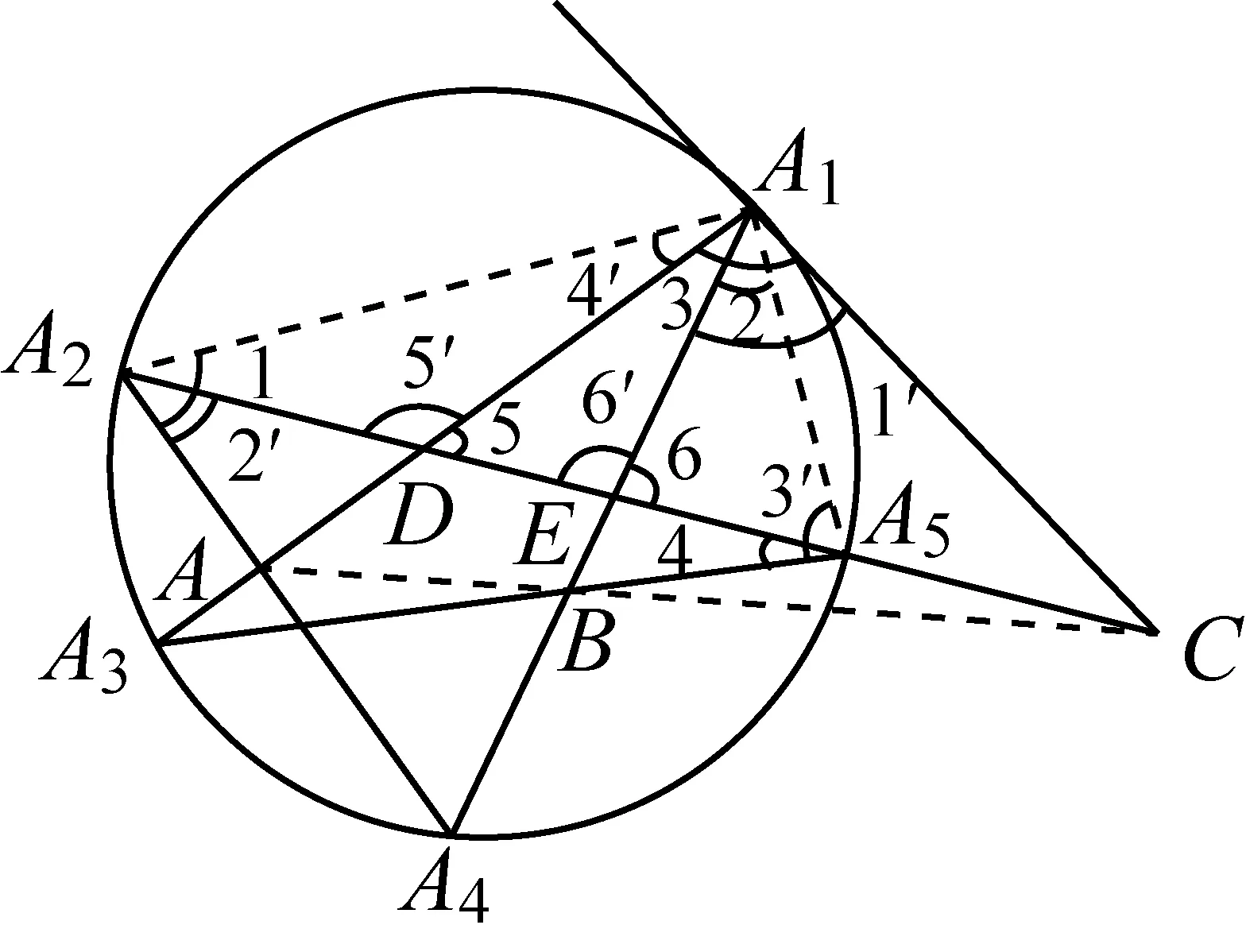
图2

以上六式相乘又易知 ∠1=∠1′,∠2=∠2′,∠4=∠4′,∠3+∠3′=∠5+∠5′=∠6+∠6′=180°,经化简可得

在△A1DE中，由梅氏定理的逆定理可知，A、B、C三点共线.

2020年10月号问题

(来稿请注明出处——编者)

2566如图，等腰△PAB中，PA=PB,过三角形中一点O作直线交边PA,PB于点E,F(不同于A,B)，使AE=OE,BF=OF.直线AO与PB交点为N,直线BO与PA交点为M,直线MF与

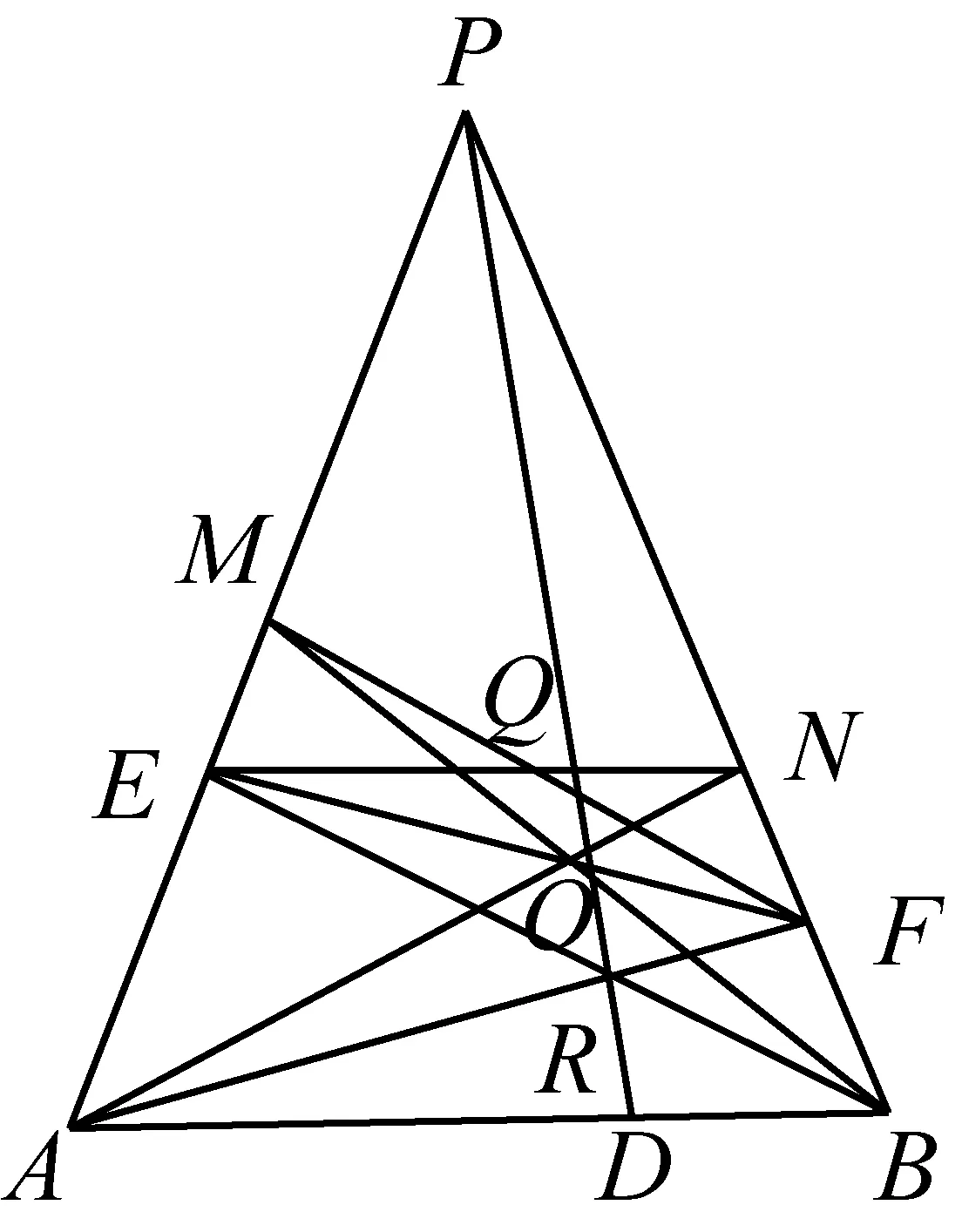
NE交点为Q,直线AF与BE交点为R.求证：P,Q,R三点共线.

(山东省泰安市宁阳第一中学 刘才华 271400)

2567已知a,b,c>0,求证：

( 陕西省咸阳师范学院基础教育课程研究中心 安振平 712000 )

2568以任意三角形各边为底边分别向外侧作同向相似的三角形，则位于外侧的三个顶点构成的三角形的重心与原三角形重心重合．

(湖北省公安县第一中学 杨先义434300)

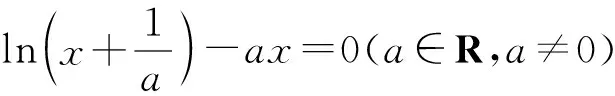
(河南省方城县教研室 邵明宪 473200)

2570如图，已知I是△ABC的内心，点G是∠B相对的旁心，D是BC边的中点，DI交AC于点F，求证：CF=GF.

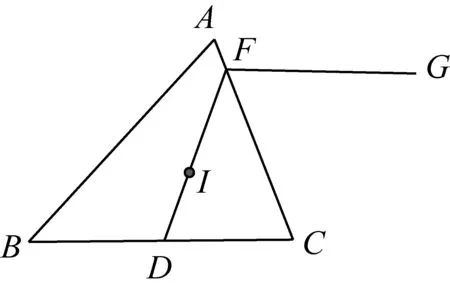
(北京市陈经纶中学 龚浩生 100020)