从历史过程中找寻数学知识的意义——“对数的运算性质”教学思考

黄光玉

(南京市金陵中学 210005)

1 问题提出

教学经验告诉我们，学生只有真正理解数学知识所蕴涵的意义，才能增强他们主动学习的动力，激发他们学习数学的兴趣，进而喜欢数学、热爱数学．要探索数学知识所蕴含的意义，就需要把学生带到数学发展的长河中，从知识产生的起点开始，让他们自主找寻知识的发生发展的一个又一个片段，经历思想的穿越，与千百年前的科学家们来一场时空对话，从纷繁复杂的数学发展历程中，慢慢捕捉到一丝光亮——客观规律.这不是仅仅获得某一个数学知识，而是学生探索科学道路上的一次历练，在探索数学知识所蕴涵的意义的过程中，学生获得探索未知世界的一般方法．那么，如何引导学生从历史过程中找寻数学知识的意义呢？本文以“对数的运算性质”教学为例，对这个问题的解决做一次探索.

2 教学过程

2.1 复习概念，强化关联

复习对数的概念，巩固指数式与对数式的本质联系[1]．

2.2 回顾历史，提出问题

课本中关于对数，有如下这样的描述：

对数是由纳皮尔发明的，纳皮尔为了简化天文学问题中的计算，在没有指数概念的情况下发明了对数，并于1614年在《论述对数的奇迹》(Mirifici logarithorum canois descriptio)中，介绍了他的方法和研究成果．

现在通用的“常用对数”，是与纳皮尔同时期的英国数学家布里格斯引入的，并于1617年出版了常用对数表．1622年，英国数学家皮德尔给出了以e为底的自然对数表．

法国数学家、天文学家拉普拉斯曾说：对数可以缩短计算时间，“在实效上等于把天文学家的寿命延长了许多倍”．

恩格斯在他的著作《自然辩证法》中，曾经把笛卡尔的坐标系、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为17世纪的三大数学发明．

师：从上述这段对数发展历史的描述中，我们发现许多的科学家、哲学家都对对数给予了很高的评价，拉普拉斯甚至说对数的发明在实效上等于把天文学家的寿命延长了许多倍．可见在数值运算，特别是在天文学的计算中，对数一定起到了简化运算的作用．

同学们，通过昨天的学习和作业，你们感受到对数运算带来的便捷了吗？

学生：没有！(苦笑)

师：那为什么历史上这么多科学家和哲学家会对对数有如此之高的评价呢？

学生：……

师：如果我们仔细看一下这段历史发生的时间，同学们就会发现对数是在距离今天大约400年的时候出现的，而对数的发明对运算的影响超过了250年，直到恩格斯在其著作中仍给予对数极高的评价．那个时代的科学家想到得到一组精确的数据可能需要花上几个小时的时间，这是轻点按键就可以得到结论的我们无法想象的．究竟对数中隐藏着怎样的奥妙呢？它真的能简便计算吗？

2.3 深入历史，探求方法

实际上在纳皮尔发明对数之前，还有许多数学家对数值之间的关系进行过研究．把时间继续向前推至1544年，有一位德国数学家斯蒂费尔写了一本名叫《整数的算术》的书．他在这本书中欣喜地写到：“关于整数的奇妙性质，可以写成整本整本的书……”那么斯蒂费尔发现了整数的什么“奇妙性质”，使他这样惊喜万分呢？[2]6-7

让我们先来看看他在书中的这个表格：

…0.1250.250.51248163264128256512102420484096……-3-2-10123456789101112

利用上述表格，若要计算16×128，可以用如下方法：

(1)找到16的“代言人”4，找到128的“代言人”7；

(2)把4和7相加，就得到11——新“代言人”；

(3)找到11作为“代言人”对应的数2048．

所以16×128=2048．

师：你能用上述方法计算4096×0.125吗？结果如何？

生1：(1) 找到4096的“代言人”12，找到0.125的“代言人”-3；

(2) 把12和-3相加，就得到9——新“代言人”；

(3) 找到9作为“代言人”对应的数512．

所以4096×0.125=512．

师：很好！你们还能利用上述表格进行哪些计算？

生2：计算：256×0.25=64．

生3：计算：4096×8=？

学生：不在表格里了！！(笑)

师：那怎么办？

学生：进一步“扩大”表格.

师：表格中的数越多，我们可以用这种方法进行计算的数值范围越广．但是这个表格仍然存在一定的缺陷：只能计算与2的整数次幂相关的运算．于是后来许多科学家包括纳皮尔在内都在此基础上建立了更加细化的表格．而现在通用的“常用对数”是与纳皮尔同时期的英国数学家布里格斯在纳皮尔对数的基础上进行改进引入的，并于1617年出版了常用对数表．

请同学们利用常用对数表(部分)，计算1.37×2.16的值．

如果想要利用表格进行计算，那么关键在于找到所计算数值的“代言人”．在常用对数表中，如何才能找到1.37的代言人呢？先在表格的第一列中寻找数值的前两位——13，在13所在行寻找数值的最后一位——7所对应的列，即1.37的“代言人”为1367，该数值与1.37的常用对数有关，由于版面印刷的限制省略了小数点，其实际含义为lg1.37=0.1367．

你能用这样的方法找到2.16的“代言人”吗？

生4：找到了，2.16的“代言人”是3345．

师：找到两个数的“代言人”，下一步呢？

生5：用0.1367+0.3345=0.4712；寻找0.4712作为“代言人”的对应的数，…

生6：表格中没有0.4712．

生7：找一个近似的，有0.4713，找到0.4713作为“代言人”的对应的数为2.96．所以1.37×2.16≈2.96．

log0123456789表尾差123456789100000 0043 0086 0128 0170 0212 0253 02940334 0374 4 8 12 17 21 25 29 3337 110414 0453 0492 0531 0569 0607 0645 06820719 0755 4 8 11 15 19 23 26 3034 120792 0828 0864 0899 0934 0969 1004 10381072 1106 37 10 14 17 21 24 283313 1139 1173 1200 1239 1271 1303 1335 1367 1399 1430 36 10 13 16 19 22 2629

续表

师：我们用这样的方法找到的结果准确吗？

生8：(使用计算器)1.37×2.16=2.9592．

师：我们从表格中查找出来的数值与准确值非常接近，由此同学们能够体会到在没有科技产品的几百年前，科学家利用寻找对应数的方式来进行计算的确能够节约许多时间！通过查表，我们找到的数值与准确值仅相差0.0008，应该说精确度还是比较高的！但如果我们要进行天文学计算的话，对数值精确度的要求会更高，如何提高精确度呢？

学生：进一步细化表格.

师：太好了！历史上的科学家们为了不断提高精确度，有的人花了毕生的心血来细化表格，给更多的科学家进行研究提供了便利．因此在长达两百多年的时间里，数学家、天文学家以及工程研究人员都要与常用对数表一类的工具为伴．

常用对数表[3]1206 lgN

对于科技如此发达的今天来说，常用对数表已经与我们渐行渐远了，那我们为什么还需要学习这些知识呢？

我们当然不再需要将表格进一步细化了，但是历史上的这些数学家们那种通过观察研究纷繁复杂的数据，得出重要结论的过程和方法仍然是值得我们去研究和学习的．

2.4 抽象验证，建构新知

让我们再回到斯蒂费尔发现整数的奇妙性质的过程．

为了计算16×128的值，我们分别找到了16的“代言人”4，128的“代言人”7，将4与7相加得到11，最后找到11作为“代言人”对应的数2048，从而得到16×128=2048．

用表格的形式呈现如下：

16×128=2048↓ ↓ ↑4 + 7 = 11

24 × 27 = 211 log216 + log2128 =?(log2(16×128))

上述运算过程，用同学们熟悉的指数形式来刻画应该如何表示？

生9：16×128=24×27=24+7=211=2048．

师：同学们根据自己的学习经验对斯蒂费尔的发现给出了形式化的表达.但历史的发展有的时候却不像我们所希望的那样具有逻辑性和系统性．在斯蒂费尔和纳皮尔的时代，还没有完善的指数概念，而在这样的情况下，他们仍然发现了数值之间的“秘密”.同学们能用我们前一节课所学习的对数的形式来刻画一下这其中的“秘密”吗？

16的“代言人”4就是log216，128的“代言人”7就是log2128，因此log216+log2128=11，11的含义是什么？

生10：11就是log22048．

师：log22048又可以表示为？

生11：log2(16×128)．

师：对于1.37×2.16的运算过程，也能用类似的方式分析吗？

1.37 × 2.16 ≈ 2.96 ↓ ↓ ↑0.1367+ 0.3345 =0.4712

100.1367 × 100.3345 = 100.4712lg1.37 + lg2.16 =?(lg(1.37×2.16))

如果推广到一般情况呢？

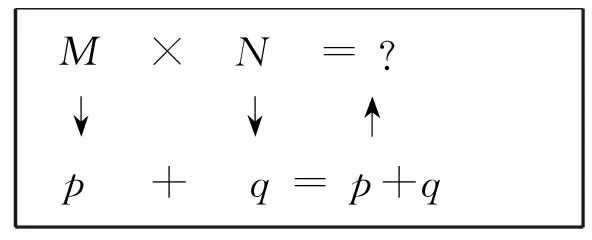
M × N = ? ↓ ↓ ↑ p + q = p+q

ap × aq = ap+qlogaM + logaN =?(loga(M×N))

通过对具体实例的分析我们终于发现了斯蒂费尔的运算方法：为了得到(M×N)的数值，我们希望找到(M×N)的“代言人”，即loga(M×N)，而loga(M×N)等于M的“代言人”logaM及N的“代言人”logaN的和，通过在数表中查找对应数的方式，将复杂的乘法运算转化为加法运算．

斯蒂费尔的方法用对数的符号呈现出来就是：loga(M×N)=logaM+logaN．这个方法是正确的吗？大家能证明吗？

生12：

证明：设logaM=p，logaN=q．

由对数的定义得M=ap，N=aq，

所以MN=apaq=ap+q，

故loga(MN)=p+q=logaM+logaN，

即loga(MN)=logaM+logaN．

师：我们终于用推理的方式验证了斯蒂费尔方法的正确性．这一结论在对数运算中非常重要，我们称其为对数的一个运算性质．能用文字语言来刻画一下这个性质吗？

生13：真数积的对数等于真数对数的和．

老师：好！一定要注意该性质的形式，将真数积的对数转化为真数对数和的运算．同学们还记得我们之前学过的指数运算性质吗？

生14：(1)ap·aq=ap+q；(2)ap÷aq=ap-q；(3) (ap)q=apq．

师：仔细对比指数运算性质ap·aq=ap+q与对数运算性质loga(MN)=logaM+logaN，你有什么发现？

学生：一样的！(笑)

师：根据指对数的相互关系，他们本质上是相同的，只是呈现形式不同．根据指数运算的另外两个性质，我们能有怎样的猜想？

生15：从ap÷aq=ap-q猜想：

生16：从(ap)q=apq猜想：logaMq=qlogaM．

师：大家都是这样想的吗？有没有其他的想法？

学生：……

师：同学们猜想的结论都是正确的，但由于时间关系，我们不能在课堂上进行证明了，请同学们在课后用前面的方法证明你们的猜想．最后，请注意上述结论成立有限制条件吗？

生17：a>0，a≠1，M>0，N>0，p∈R．

2.5 应用举例，运用新知

例1：已知lg2≈0.3010，lg3≈0.4771，试求下列各式的值(结果保留4位小数).

(1) lg8； (2) lg12；(3) lg13.5；(4) lg5.

解：(1) lg8=lg23=3lg2≈3×0.3010=0.9030；

(2) lg12=lg(22×3)=lg22+lg3=2lg2+lg3≈2×0.3010+0.4771=1.0791；

1-0.3010=0.6990．

例2：求下列各式的值：

(1) log2(23×45)； (2) log5125．

解：(1) log2(23×45)=log2(23×210)=

log2213=13log22=13；

(2) log5125=log553=3log55=3．

思考：已知lg1.37=a，则lg137=______．

解：lg137=lg(1.37×100)=lg1.37+lg100=lg1.37+2，

因为lg1.37=a，所以lg137=lg1.37+2=a+2．

2.6 复习巩固，课后练习

回顾本节课，同学们共同经历了在没有科技设备的情况下，人们进行简便运算的一些过程，从中找到了对数运算的相关性质，并证明了其正确性．

2.7 预设生成，板书呈现

3 教学反思

“对数的运算性质”是苏教版必修1第3章对数函数的第2课时．在前一课时，我们通过对指数式ab=N的进一步研究引入了对数的概念，得到与指数式本质相同的另一种表达形式logaN=b．学生对对数的概念有了初步的认识，但对研究对数的意义还不是非常清楚，特别是在信息技术和科技手段日益强大的今天，想要计算出课本中出现的那些对数式的值，只要在手机屏幕上轻松点击数下，就可以得到精确度极高的结果，如今，中学生学习这一知识的意义究竟何在？

3.1 黑暗与曙光

每次在高一讲解对数运算性质这一内容的时候，我都会比较茫然，站在学生的角度，总会提出这样的问题——究竟是如何想到对数具有这样的性质的呢？虽然现代技术手段越来越发达了，但是如果我们仅是通过科学技术手段让学生知道这个结论，然后不断操练熟悉这个结论吗？有很长的一段时间，我都在不断追问这个问题，终于当我在翻阅对数知识的发展历程时，找到了解决的方法——回到对数发展的起点，让学生在课堂上感受一次从纷繁复杂的数据中寻找数量之间关系的过程．

3.2 选择与放弃

虽然我终于找到了教学设计的方向，但是面对纷繁复杂的素材，如何能在一堂课的时间里把这些内容用合适的方式呈现出来，又成了我面前的一个难题．比如，纳皮尔在研究对数的过程中，投入了很多的精力，他将长达近20年的业余时间都奉献给了对数运算，得到了许多有价值的结果，还有很多数学家为了对数计算能够更加便捷，还制作了一些运算的工具，……但这些内容比较适合由老师直接呈现，学生无法参与其中，这样的课堂只是陈述事实的讲堂，怎样才能让学生动起来呢？带着这个问题，我从大量的实际背景中选定了两个材料：一个是德国数学家斯蒂费尔对于整数性质的研究，一个是在对整数性质分析的基础上，借助数学用表，推广到对一般数据运算的分析．

3.3 收获与遗憾

我们已经进入大数据时代，每天都有海量的数据被记录下来，我们将要面对的世界比几百年前的世界更加复杂，虽然随着科学技术的不断进步，我们进行数据分析的工具更加先进了，但是我们分析数据的能力是不是也在不断进步呢？在数学的课堂上，教师带着学生一起学习这些“古老”的知识不是用它们来填装我们的大脑，而是希望能通过切实的体验，丰富学生处理问题的经验，当学生面对新的世界，遭遇新的问题时，他们可以尝试找到方法来解决．社会的不断进步，要求我们的学生能够有解决新困难的勇气和方法，这才是真正的学习．一节课的时间是非常有限的，教学设计的有效达成，还需要考虑学生的课堂状态，因此本节课中留给学生体验和考察数据之间关系的过程还略显仓促，如果能有更充裕的时间会更好．另外，随着课程教学改革的不断深入，加强学生对数据分析能力的培养也不是一节课就能够实现的，这需要教师对课程教学有整体的规划和研究．