基于云重心Shapley值法的矿产资源开发收益分配研究

李 婷，周进生

(中国地质大学(北京)经济管理学院，北京 100083)

0 引 言

矿产资源是人类社会发展的重要物质基础，矿产资源的合理开发利用不仅促进了资源地经济的快速发展，还对我国经济转型发挥着重要作用。然而，大量资源型区域的矿产资源已经被人类过度开发利用，并造成了生态破坏、资源耗竭、环境污染等一系列问题。当地居民不仅没有因为矿产资源的开发而改善生活质量，反而还要承受因矿山企业粗犷式开采而造成的环境问题，导致资源富集区正面临着“资源诅咒”的处境，引发了一系列矿区冲突事件。究其根本，是矿产资源收益分配的不合理造成的，因此如何解决矿产资源开发收益共享中存在的问题，构建和完善我国矿产资源开发收益共享机制，对于维护矿产资源地和谐开发以及可持续发展有着重要意义。

国内外学者对矿产资源开发过程中的收益分配问题进行了广泛的研究。企业社会责任理论(CSR)政策框架的提出虽然提高了当地社区、基层组织、工会等利益主体的参与度，但仍不能有效解决利益主体的收益分配冲突[1]。由于资源开发收益分配不合理而产生的冲突会对社会稳定性产生负面作用，影响国家经济的发展[2]，因此，为避免冲突的产生，应建立合理的税收制度[3]和矿山产权制度[4-5]，并通过一套完善的法律体系对其进行约束[6]。

Shapley值法是由美国博弈论专家SHAPLEY于1953年提出的，用于解决多人合作博弈的模型。Shapley值法将各利益相关者做出的边际贡献作为收益分配的原则，避免了平均分配，可以很大程度地减少各成员对于分配结果的不满。因此，学者们运用Shapley值法对不同研究对象的博弈群体收益分配问题进行了研究[7-8]。但由于Shapley值法没有根据研究对象的具体特点对收益进行分配，因此学者们对该收益分配模型进行了改进[9-13]。随着Shapley值法研究的深入以及应用的广泛，部分学者将优化后的Shapley值收益分配模型运用到矿产资源开发收益分配中，使得矿产资源开发利益主体的收益分配更加公平合理[14-17]。

通过对前人的研究总结发现，关于矿产资源开发收益分配问题的研究，学者们主要集中于定性研究，对于如何量化矿产资源开发利益相关者间的收益分配，还需进一步研究。同时，运用Shapley值法在矿产资源开发收益分配领域研究较少且相对不成熟。运用Shapley值法所构建的收益分配模型，进行的收益分配是根据合作过程中各利益相关者的边际贡献，具有一定的合理性。但是矿产资源开发过程中，各利益相关者承担的风险不同，如政府承担勘探、环境治理风险等，矿山企业承担矿产资源含量未知、矿价市场不稳定等风险，矿区居民承担环境破坏等风险；各利益主体在矿产资源开发过程中所投入的资金也各不相同，政府和企业因对矿产资源勘探和开发需投入较多的资金、人力、技术，而矿区居民在矿产资源开发过程中主要投入为土地；利益主体具有的创新能力各不相同，政府主要是在勘查技术以及政策制度上进行创新，企业是在开发技术、制造矿产品工艺方面进行创新，矿区居民的创新体现在打破传统思想，配合矿产资源合理开发，以土地入股矿山企业，接受岗位培训、征地拆迁方面的思想创新；矿产资源开发后利益主体对生态修复的支持力度各不相同，矿山企业往往为了追求自身利益而逃避修复生态环境，最终导致政府和居民承担较多的生态环境修复。其中风险分摊系数、创新能力以及对生态修复的支持力度这些影响因素随机模糊性强，具有不确定性，且难以量化，而云重心法是解决定性与定量间不确定转换的有效方法。因此，为了改善Shapley值分配法具有的缺陷，本文在学者们已有的研究基础上，通过分析总结大量文献，选择具体实例，运用Shapley值法构建了政府、矿山企业、矿区居民三方利益主体的收益分配模型，并引入风险分摊系数、投资比重、创新能力、生态修复支持力度四个影响因素，运用云重心法计算各利益相关方的收益修正值，使得收益分配方案更具有合理性和实际性。

1 相关利益主体的诉求及博弈分析

矿产资源开发过程中涉及到的核心利益相关主体包括中央政府、地方政府、矿山企业和矿区居民。矿产资源开发对于社会发展是必不可少的，中央政府通过制定矿产资源开发政策保证矿产资源的合理开发与利用，中央政府不仅要保证自身的财税收入，同时也有责任使社会获得综合效益最大化。因此，中央政府的利益诉求主要为保证政策落实到位、增加中央财税收入、保证资源地经济稳定发展以及改善资源地的生态环境等。地方政府既需要代表国家对资源地矿产资源进行管理，又需要为当地经济谋发展，同时还要考虑自身的税收问题。因此，地方政府的利益诉求为自身财税收入最大化、增加当地GDP及保护当地生态环境等。矿山企业作为矿产资源的开发主体，通过获取探矿权和采矿权后从事矿产资源勘查开发来获得收益，矿山企业所追求的即利益最大化。因此，矿山企业的利益诉求主要为获得高收益并且能够长期发展。作为利益相关者中最缺乏话语权的矿区居民，不得已配合政府和企业进行矿产资源开发，通过当地矿山企业给予相应的就业机会和经济补偿维持生活。因此，矿区居民的利益诉求主要为拥有就业机会、生存环境改善等。

在矿产资源开发过程中，各利益相关方为了使自身需求得到满足，实现各自利益的最大化，会相互进行博弈。

1) 中央政府和地方政府。尽管中央政府是矿产资源的所有者，但由于中央政府不能直接对各资源地的资源开发进行管理，只能委托地方政府代表国家对资源开发进行监管。而地方政府又分为省、市、县、乡镇、村，最终分给当地基层政府的税费数额非常少，因此，中央政府和地方政府的博弈关系主要在税费的分成问题上。

2) 政府和矿山企业。在进行矿产资源开发的过程中，由于开发技术水平有限，会对资源地的生态环境造成一定程度的破坏，但是矿山企业为了追求自身利益最大化，减少成本支出，对生态修复持消极态度，而政府作为管理者，会对矿山企业的生态破坏行为进行监督与惩罚。同时，由于我国税收体系不健全，矿山企业常常认为国家征收了过多的税费。因此，政府和矿山企业的博弈主要体现在税收以及企业是否对资源地进行合理的生态经济补偿。

3) 政府和矿区居民。政府作为土地的所有者，矿区居民作为土地的使用者，在矿产资源开发过程中，两者会在土地的征收问题上进行博弈。

4) 矿山企业和矿区居民。由于矿山企业对资源地的生态破坏，矿区居民作为直接受害者，会向矿山企业索要相应的经济补偿费，另外，矿山企业还需支付矿区居民相应的征地费以及向居民提供就业机会，使得当地居民能够得以生存。但由于矿山企业持有的消极态度往往引发双方矛盾升级，因此两者有必要进行博弈来使得双方利益均得到最大化。

2 研究方法及数据说明

2.1 基于Shapley值的矿产资源开发收益分配模型的建立

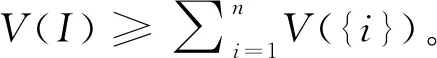
在矿产资源合作开发集合I下，由特征函数决定的φi(V)表示其中一个局中人i所得到的收益分配，利益相关者在矿产资源开发过程中分配方案可以表示为：φ(V)=(φ1(V),φ2(V),…,φn(V))。当φi(V)同时满足对称性、可加性和有效性3个条件时，矿产资源合作开发过程中利益主体的收益分配方案存在唯一Shapley值，见式(1)。

φi(V)=

i=1,2,…,n

(1)

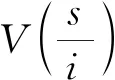
2.2 基于云重心的Shapley值收益分配模型

云重心法是在云理论的基础上发展起来的新的评估方法，体现的是定性和定量的不确定转换，解决了主观性较强、随机模糊方面的问题，能够有效地进行模糊数学挖掘和信息处理。正态云三个数字特征分别为期望值Ex、熵En和超熵He，Ex为正态云的重心位置，En为正态云的期望宽度，He为正态云的离散度和隶属度的随机程度的改变度。云重心是由重心位置和高度共同决定的，当a为正态云的重心位置，即期望值Ex，b为云重心的高度时，云重心表示为：T=a×b。基于云重心的Shapley值法的收益分配模型具体的计算过程如下所述。

1) 各指标的云模型。矿产资源开发收益分配模型中有4个影响因素，可用4个云模型来表示，分别为风险分摊系数、投资比重、创新能力、生态修复支持力度，若有m位专家为各影响因素赋值，可以得到m个精确数值。对于定量指标，各指标云模型的数字特征值Ex、En，见式(2)和式(3)。

Ex=(Ex1+Ex2+…+Exm)/m

(2)

En=[max(Ex1,Ex2,…,Exm)-

min(Ex1,Ex2,…,Exm)]/6

(3)

2) 构建四维综合云。用云模型表示以上四个指标，可以构建一个四维综合云，当综合云的形状和位置发生相应的变化时，云重心也会发生相应的变化，因此可以用云重心的变化来反映系统状态。四维云重心用一个向量表示为T=(T1,T2,T3,T4),其中，Ti=ai×bi,i=1,2,3,4，ai为第i指标(云模型)的期望值；bi为第i指标(云模型)归一化后的权重。

3) 确定各指标权重。确定指标权重的方法较多地采用层次分析法、灰色关联度法等。本文运用排队论的方法确定各指标权重以减少人为因素的影响，各指标的权重wi满足式(4)。

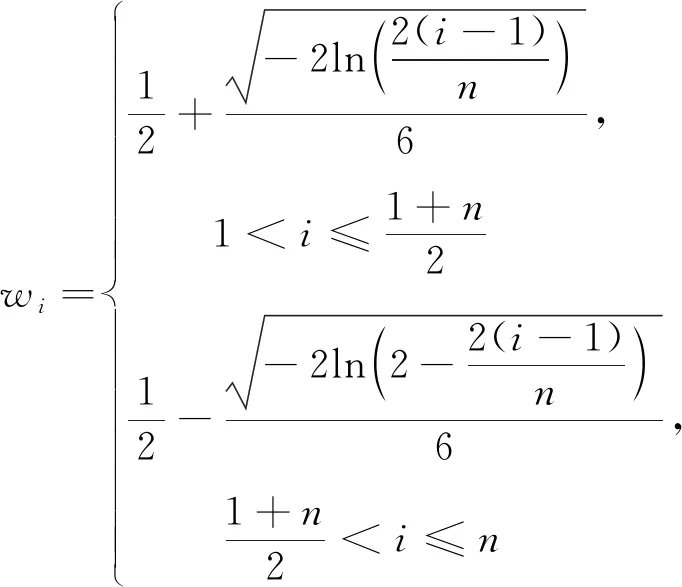
(4)

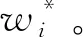
4)确定四维综合云的加权偏离度。不同环境下的四维综合云的加权偏离度θ值(-1<θ<0)越大，说明此理论模型偏离理想综合云的程度越大。理想状态综合云指特定矿产资源开发收益系统中，风险最大、投资比重最大、创新能力最强以及生态补偿支持力度最高的一种状态，此时状态的云重心为式(5)。

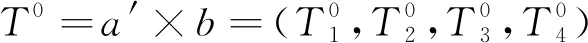
(5)

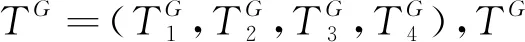
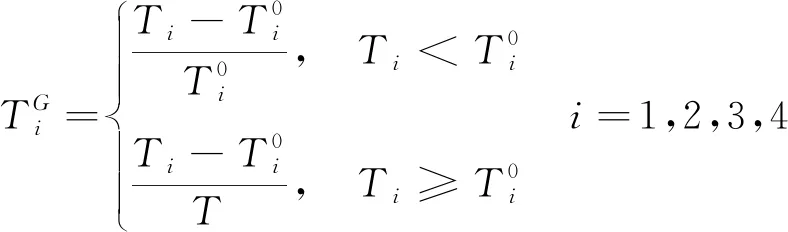
(6)

加权偏离度θ可表示为式(7)。

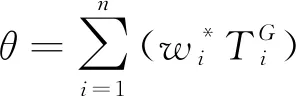
(7)

5) 计算矿产资源开发各利益主体收益修正值。对各利益主体的θ归一化处理后，得到各成员的权重θ*，进而可得矿产资源开发过程中各利益主体的修正值Δφi(V),见式(8)和式(9)。

Δφi(V)=V(n)×ΔRi

(8)

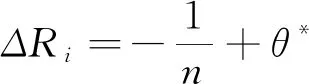
(9)

式中：ΔRi为各利益主体的收益修正权重；V(n)为矿产资源开发过程中各利益主体都合作情况下的最大收益。

6) 计算各利益主体分配的实际收益，见式(10)

φi(V)*=φi(V)+Δφi(V)

(10)

本文基于云重心法的Shapley值收益分配模型，充分考虑了不同分配因素对矿产资源开发收益的影响，解决了定性指标向定量指标转换过程中主观性、模糊性和随机性的问题，使得收益分配更加公平合理，利益主体之间能够更加积极地进行合作，矿产资源开采环境更加和谐。

2.3 数据说明

矿产资源开发利用过程中的核心利益相关者分别为中央政府、地方政府、矿山企业、矿区居民。由于中央政府和地方政府的收益来源主要为矿山企业通过开发利用矿产资源后所缴纳的资源税费等，且二者的收益分配实际上是不同级别政府的税收再分配。故本文对于中央政府和地方政府的博弈问题不作重点讨论，主要分析政府、矿山企业、矿区居民通过合作博弈后获得的收益分配的过程。

西部某铅锌矿公司，是主要从事铅锌采选业务的矿山企业，主营铅锌生产、销售，产品涵盖铅精矿、锌精矿及银。本文通过对西部某铅锌矿实地调研得到政府、矿山企业、矿区居民的实际收益情况。

3 结果与分析

3.1 Shapley值法分配矿产资源开发收益

已知西部某铅锌矿各利益主体单独和合作进行矿产资源开发时的收益分配情况。政府、矿山企业、矿区居民分别用1、2、3表示，政府指各级政府，矿山企业指铅锌矿资源开发企业，矿区居民指企业所在地涉矿的村民。 在矿产资源开发过程中，若单独开采，政府收益为V(1)=100万元，矿山企业收益为V(2)=40万元，矿区居民收益为V(3)=20万元；若有两个利益主体合作开发，政府和矿山企业合作V(1∪2)=240万元，政府和矿区居民合作V(1∪3)=180万元，矿山企业和矿区居民合作V(2∪3)=80万元；若三个利益主体合作进行矿产资源开发，则政府、矿山企业、矿区居民合作所获得的收益为V(1∪2∪3)=320万元，见表1。

运用Shapley值法计算利益相关者的收益分配额，具体计算及结果见表2。

表1 收益分配表Table 1 Revenue distribution table

表2 西部某铅锌矿开发中利益相关者的Shapley收益值Table 2 Shapley revenue of stakeholder in the developmentof a lead-zinc mine in western China

通过计算可得式(11)～式(15)。

φ1(V)+φ2(V)+φ3(V)=320万元

(11)

φ1(V)>V(1),φ2(V)>V(2),

φ3(V)>V(3)

(12)

φ1(V)+φ2(V)>V(1∪2)

(13)

φ1(V)+φ3(V)>V(1∪3)

(14)

φ2(V)+φ3(V)>V(2∪3)

(15)

由上述表达式可以看出，三个利益相关者在选择合作开采矿产时所获得的收益比不合作时获得收益要高，即各利益相关方共同合作的Shapley收益值大于单独开采或者任意两者合作开采所获得的收益。因此，政府、矿山企业、矿区居民更倾向于选择合作开发。

3.2 基于云重心的Shapley值的矿产资源开发收益分配

从修正的Shapley值法的基本思想出发，需要计算出政府、矿山企业和矿区居民的收益修正系数。邀请4位专家对矿产资源开发过程中的风险分摊系数、投资比重、创新能力、生态修复支持力度几个方面进行评价，见表3。

根据式(2)～式(4)，可以计算出矿产资源开发过程中各个影响因素的期望值、熵和权重，见表4和表5。

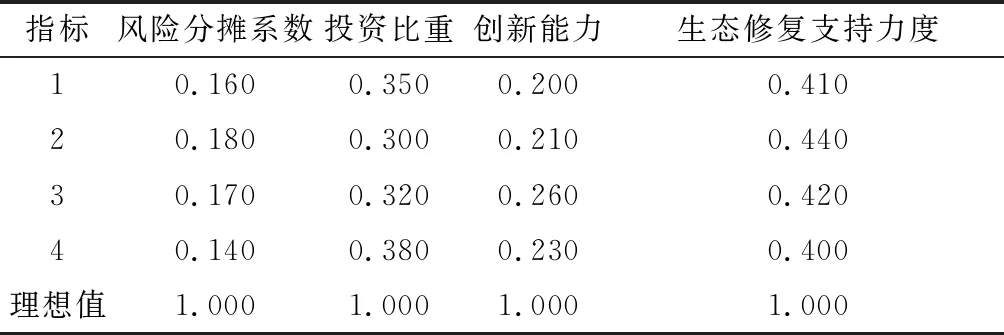
表3 矿产资源开发过程中各个影响因素的理想状态Table 3 Ideal state of each influencing factor in the processof mineral resources development

表4 矿产资源开发过程中各个影响因素的期望值和熵Table 4 Expectation and entropy of each influencing factorin the process of mineral resources development

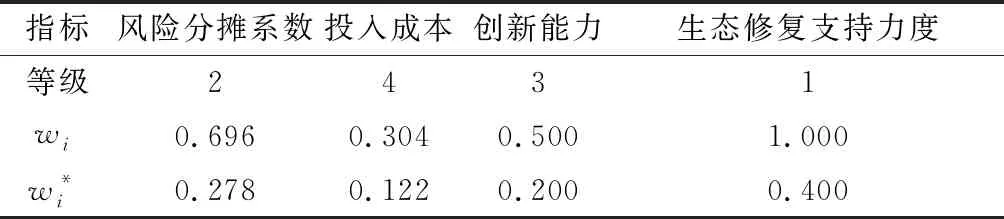
表5 矿产资源开发过程中各个影响因素的权重Table 5 Weights of each influencing factor in the processof mineral resources development

可以计算出政府四维综合云的云重心T为：T=a×b=(0.045,0.041,0.045,0.167)。

根据式(5)计算政府理想四维综合云的云重心T0为：T0=a×b=(0.278,0.122,0.200,0.400)；根据式(6)将四维综合云归一化后，TG=(-0.838,-0.663,-0.775,-0.583)；根据式(7)计算可得出政府四维综合云与理想综合云的偏离度θ=-0.702。同理可求出矿山企业、矿区居民的四维综合云的偏离度为-0.678、-0.747。

根据式(8)和式(9)可得：

ΔR1=-0.003,ΔR2=-0.014,ΔR3=0.018；

Δφ1(V)=320×ΔR1=-1.073；

Δφ2(V)=320×ΔR2=-4.631；

Δφ3(V)=320×ΔR3=5.704。

根据式(10)，可以计算出政府、矿山企业、矿区居民经修正后所得的利益分别为：

φ1(V)*=φ1(V)+Δφ1(V)=171.927万元；

φi(V)*=φ2(V)+Δφ2(V)=88.369万元；

φi(V)*=φ3(V)+Δφ3(V)=59.704万元。

根据以上的计算结果，将矿产资源开发收益分配方式进行对比分析，见图1。

图1 不同收益分配结果对比Fig.1 Comparison of results of differentrevenue distributions

由图1可知，与传统Shapley值收益分配法相比，改进后的Shapley值收益分配法使得各利益主体的收益发生了变化，即政府的最终收益值由173万元降为171.927万元，减少了1.073万元；矿山企业的最终收益值由93万元降为88.369万元，减少了4.631万元；矿区居民的最终收益值由54万元上升为59.704万元，增加了5.704万元。改进后的收益分配模型综合考虑了矿产资源开发中，各利益相关者所承担的开发风险、投资比例、创新能力以及生态修复支持力度，使得各利益相关方的付出和收益更加匹配，因此改进后的收益分配方案更加公平合理。

4 结 论

1) 根据云重心Shapley值法，计算结果表明，政府、矿山企业、矿区居民的最终利益分配系数为：0.537、0.276、0.187。其中，政府在矿产资源开发过程中所获得的收益最高，是由于政府身为矿产资源的所有者，依法对矿产资源进行管理；矿山企业所获得的收益次之，是由于利益主体所进行分配的利益均由矿山企业在开发矿产资源时所获得，矿山企业是矿产资源开发的经济主体；矿区居民所获得的收益最少，是由于矿区居民仅拥有土地使用权而不具有矿产资源所有权，因此不会获得收益分配，但因矿区居民是环境破坏负效应的直接承担者，故应获得一定程度上的资源补偿。

2) 通过将传统Shapley收益值与引入影响因素修正后的Shapley收益值进行比较和分析，政府的实际分配收益值下降，是由于在矿产资源开发过程中，政府的创新能力较弱，且因为体制因素，不能承担过高的风险；矿山企业的实际分配收益值下降，是由于企业在矿产资源投资开发的整个过程中承担着过高的风险，虽然不断在技术装备上进行创新，但由于政府监管还要支付破坏矿区生态坏境而发生的成本，企业最终还是以盈利为目的，故矿山企业为了使自身利益最大化，会采取各种“阴暗化”手段，即为了减小其支出成本，排放未经处理的污染物，使得资源地生态环境状况更加糟糕；矿区居民的实际收益值上升，是由于矿区居民处于弱势，拥有较低的话语权，但却要面临因环境破坏带来的生存风险。根据上述分析，改进后的收益分配模型具有明显的优越性，具体表现在利益相关方的付出与所获得收益成正比，提高了合作团体的稳定性；同时，通过分析矿产资源开发中的政府、矿山企业、矿区居民所承担的风险、所进行的投资和创新以及生态支持力度的问题，使用改进后的模型更加符合实际情况。