基于流固耦合的轴流泵压力脉动与动应力的关联性研究
2020-12-17贺玉珍郭艳磊
贺玉珍,郭艳磊
(1.临夏州水电局河道管理站,甘肃 临夏 731100;2.兰州理工大学能源与动力工程学院,兰州 730050)
轴流泵以其大流量、低扬程及高效等特性在我国调水工程及城市给排水工程方面得到广泛应用,轴流泵运行的稳定性问题也随之得到了相关学者的重视[1]。通过叶轮旋转,将机械能转化为流体的动能和压能,能量转换过程中,叶片受到流体动反力作用发生变形,叶片的变形又会影响流场结构,这是一个典型的双向流固耦合过程[2,3]。轴流泵内流场为大雷诺数三维瞬态非定常流动[4],且流动呈现明显的周期特性,所以叶轮所受载荷同样表现出明显的非定常周期特性,载荷的周期波动会引起结构的振动及噪音,甚至会影响机组的稳定运行。因此,研究轴流泵叶轮的振动特性具有重要的理论价值,对增加泵站机组的使用寿命、防止结构破坏都具有重要意义。
叶片在流体载荷作用下会发生变形,叶片变形会引起流场结构的变化,从而进一步影响叶片所承受的载荷,因此对轴流泵结构域和流体域进行双向流固耦合计算是十分必要的[5]。近年来,流固耦合技术广泛用于流体机械的结构静力学和结构动力学分析中[6-12]。刘厚林等[8]应用双向流固耦合方法对导叶式离心泵的外特性和内流场进行分析,研究了流固耦合作用对外特性影响的内流机理。裴吉等[9]应用同步求解,对离心泵内流场和叶轮结构响应进行数值研究。周颖等[10]采用双向流固耦合分析了轴流泵反向旋转时的压力大小和分布。
流固耦合技术已经在流体机械,特别是水轮机上得到了广泛的应用[13-18],并取得了较好的成果。
为了对轴流泵流体域和结构域进行双向流固耦合计算,从而获取结构域在流固耦合作用下的力学响应特性,本文采用双向流固耦合技术,预测了轴流泵叶轮在流体作用载荷下,其力学响应特性和应力应变分布规律,为轴流泵进一步的结构动力学分析及优化提供一定的基础。
1 流固耦合计算方法
1.1 流体控制方程组
轴流泵内流体为连续非定常不可压缩流体,其连续性方程和动量方程张量表现形式为:
(1)
(2)
式中:p为静压;ρ为介质密度,取1 000 kg/m3;v为水的动力黏性系数,取1.519×10-6Pa·s。
1.2 湍流模型
本文主要采用k-ε模型研究轴流泵内流场的流动特性及与结构的相互耦合作用,方程具体形式为:
k方程:
(3)
ε方程:
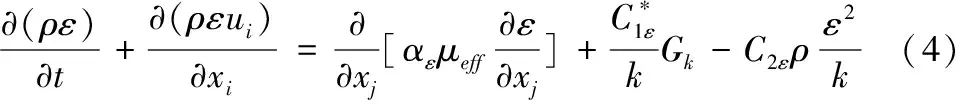
其中:
式中:ε为湍动能和耗散率;Gk为湍动能生成项;模型常数C1ε=1.42,C2ε=1.68,Cμ=0.0845,αk=αε=1.39。
1.3 结构动力方程
对于任何结构而言,质量,材料阻尼,结构刚度和载荷是影响结构动力学影响的重要因素,结构动力方程如下:
充分保障农民土地处分权是保护农民土地产权的重要途径之一。中国农民的土地产权问题在法律规定上含糊不清,需要进一步详细阐述农民土地处置权和农民土地产权的具体规定。政府可以通过不断完善信访制度,充分了解农民的意愿,充分把农民的意愿落实在政策的每一个方面;并通过对农村干部的政治修养和规范管理水平的不断提高,加强干部们的党性建设水平,坚持走群众路线,进一步保障农民的土地财产权。
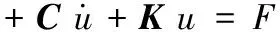
(5)
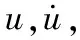
1.4 双向同步流固耦合求解原理
本文应用CFX和workbench相耦合的方法,实现轴流泵流体域和结构域的双向耦合联合求解。具体过程是:对流体域和结构域设置相同的计算时间和时间不长,首先计算流体域,其数据的传递是双向的,流体分析结果(压强)传递给固体结构分析,然后固体结构分析的结果(位移、速度以及加速度等)反向传递给流体分析,依次进行逐步推进,如此反复迭代求解,直到计算满足收敛条件或者达到计算步长。
1.5 基本参数、网格划分和边界条件
本文所研究的模型为ZBM791-1000型轴流泵,其基本参数如表1所示。

表1 轴流泵的主要参数
流体计算域包括进口段,转轮段,导叶段,出口段;固体计算域主要指叶轮。为了减少网格单元数量以及节点数量以降低计算成本和得到更加精确的计算结果,采用CFX前处理软件ICEM对流体计算域进行六面体网格划分,固体计算域网格运用WORKBENCH中自带网格工具划分四面体网格。其中流体域网格单元数量为556万,固体域网格数量为67万。网格如图1及图2所示。

图1 流体计算域网格

图2 固体计算域网格
流体域边界条件设置如表2。
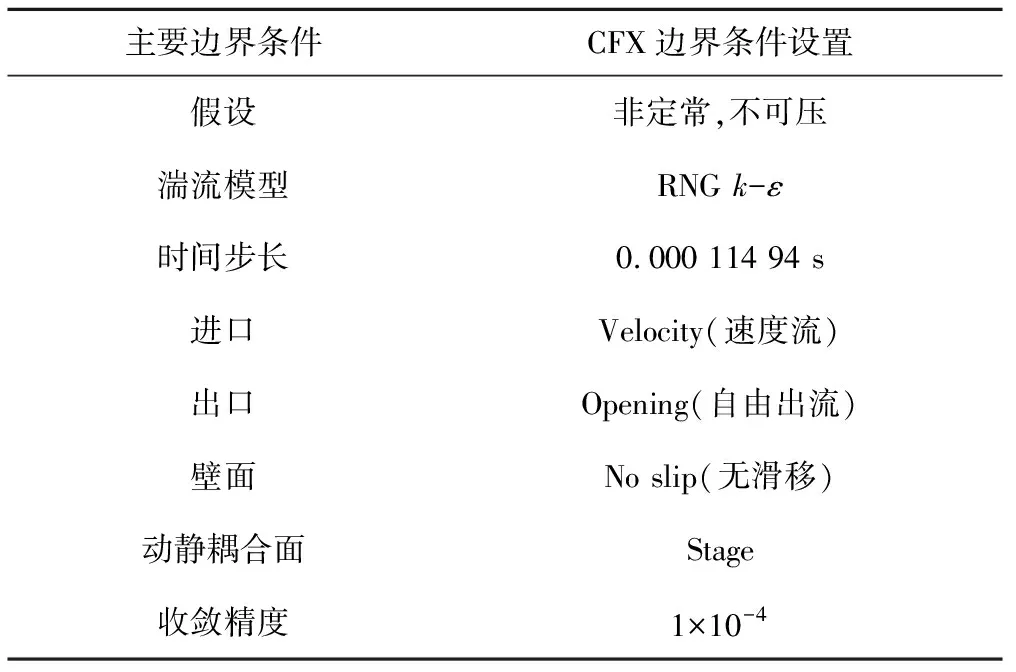
表2 边界条件
流体域非定常计算以定常计算为初始值,时间步长设置为叶轮每转过1°的时间,即0.000 114 94 s,结构域设置同样的时间步长。结构域对轴承处采用轴向和径向约束,采用远端位移实现转子转动。
2 计算结果及分析
2.1 压力脉动监测点布置
为了监测轴流泵内部流动的压力变化,分别在叶轮进口、叶轮出口两个截面上共设置8个监测点,即每个截面上4个监测点,其监测点半径分别为:80、100、120、140 mm,从轮毂到轮缘沿半径方向分布,监测点的布置如图3所示。
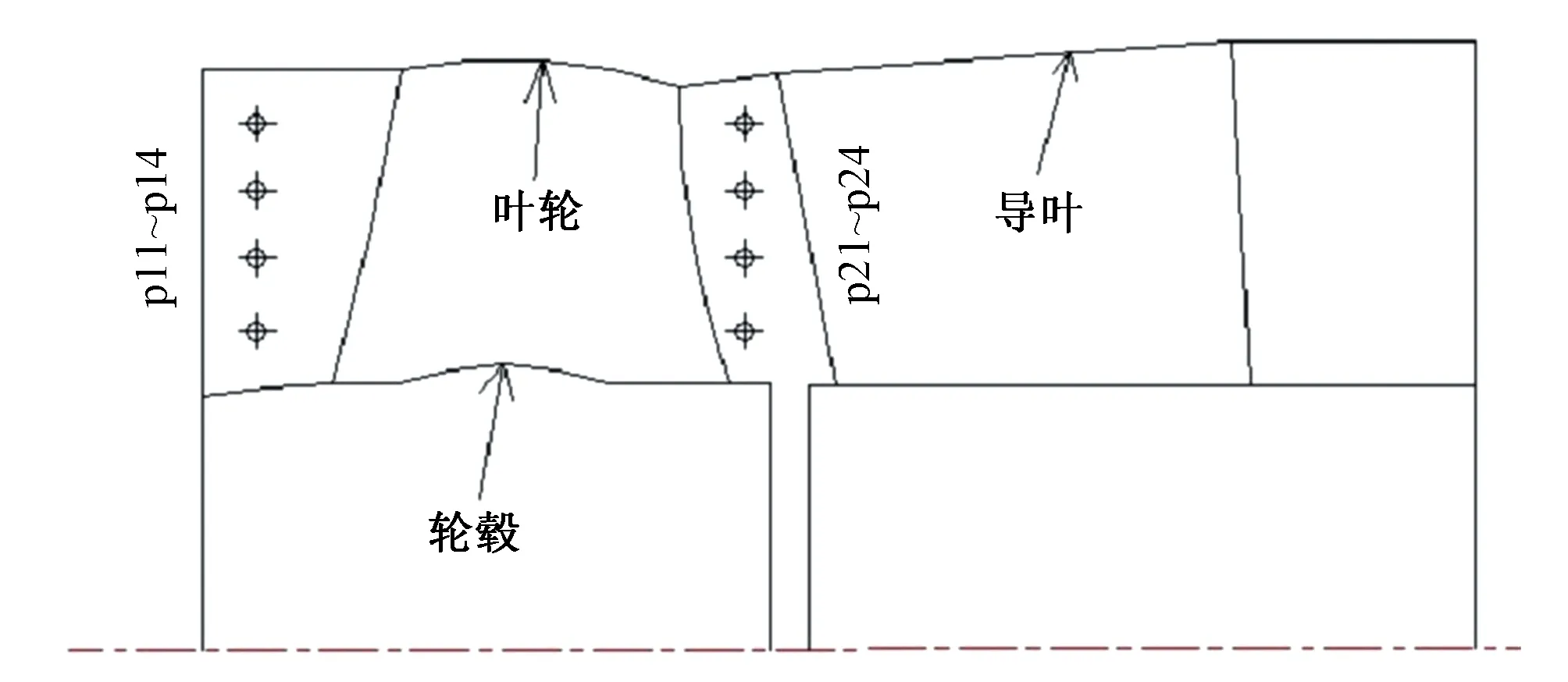
图3 压力脉动监测点布置
2.2 流固耦合作用下叶轮应力分析
图4所示为在0.7~1.2倍设计工况下,在同一时刻轴流泵叶轮的等效应力分布。由图4所示:在各种工况下,叶轮最大等效应力均出现在叶片工作面靠近进水边的轮毂位置处,远离该位置,则等效应力依次递减。此外,叶轮工作面进口轮毂位置处最大等效应力与流量呈现负相关的关系,这是流量增大叶轮叶片载荷下降所导致的。
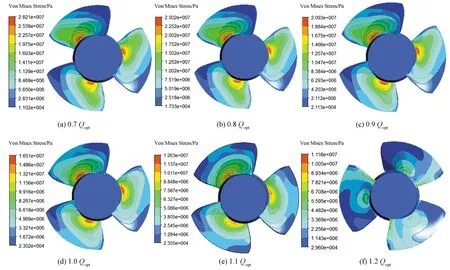
图4 叶片表面应力分布
2.3 流固耦合作用下叶轮变形分析
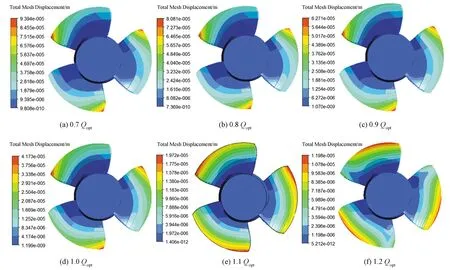
图5 叶片位移变形分布图
2.4 轴流泵叶轮动应力特性分析
经分析可知,叶轮在各个工况下所受到的最大应力远远低于其强度极限,所以叶轮不会因强度不足而失效,但是泵内流动呈现明显的非定常周期特性,也就是说叶轮所受到的载荷亦将呈现明显的周期特性,交变载荷容易诱发疲劳失效,需要注意叶轮的疲劳失效问题。
图6所示为在3个工况点,叶片最大等效应力在一个周期内的时域分布图,由图6可知,在不同工况下,等效应力呈现明显的非定常周期特性,经过傅里叶变换,基频与叶频相当,叶片载荷波动幅值较小,叶片载荷随着流量增大而减小。

图6 叶轮最大等效应力时域图
2.5 流量对轴流泵叶轮应力及变形的影响
图7为叶轮的最大等效应力及最大变形随流量变化曲线。由图7可知,叶轮最大等效应力和最大变形值均与流量呈现负相关关系,即随着流量的增大,最大等效应力和最大变形值均减小。
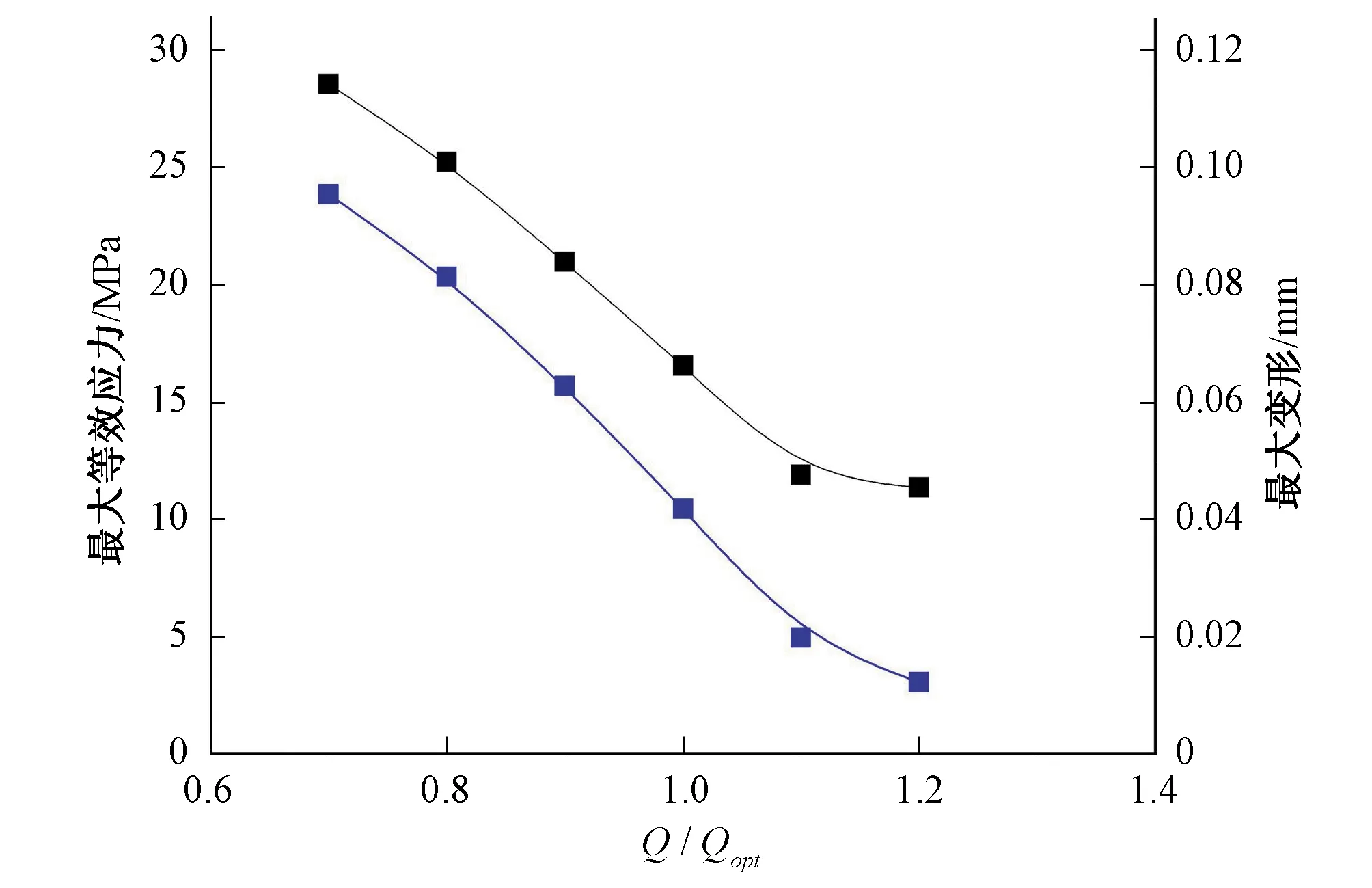
图7 不同流量下叶轮的最大等效应力及最大变形
2.6 压力脉动结果分析
2.6.1 叶轮进口压力脉动分析
图8(a)、8(b)所示分别为设计工况下轴流泵叶轮进口不同半径监测点处的压力脉动时域图和频域图。分析发现,尽管叶轮对水流的作用是水流进入叶片之后,但叶片对来流的扰动在水流进入叶片之前便存在了,所以在叶轮进口截面各监测点处都存在比较明显的压力脉动,因此,在轴流泵的水力设计中应该对其进口流场给予重视。压力脉动幅值从轮毂到轮缘逐渐增大,另外,各监测点的压力脉动频率均为叶轮转频(24.17Hz)的3倍(72.5 Hz),正好与叶片通过频率相一致。说明轴流泵叶轮进口前的水流压力脉动主要由叶轮叶片通过频率决定。

图8 叶轮进口压力脉动时域频域图
2.6.2 叶轮出口压力脉动分析
图9(a)、9(b)所示分别为设计工况下轴流泵叶轮出口不同半径监测点处的压力脉动时域图和频域图。同叶轮进口类似,叶轮出口处监测点的压力脉动幅值从轮毂到轮缘逐渐增大,且主频仍是叶轮叶片通过频率。但是压力脉动幅值远远低于进口,其原因可能是由于导叶的作用制约了水流的压力脉动,使其趋于稳定。
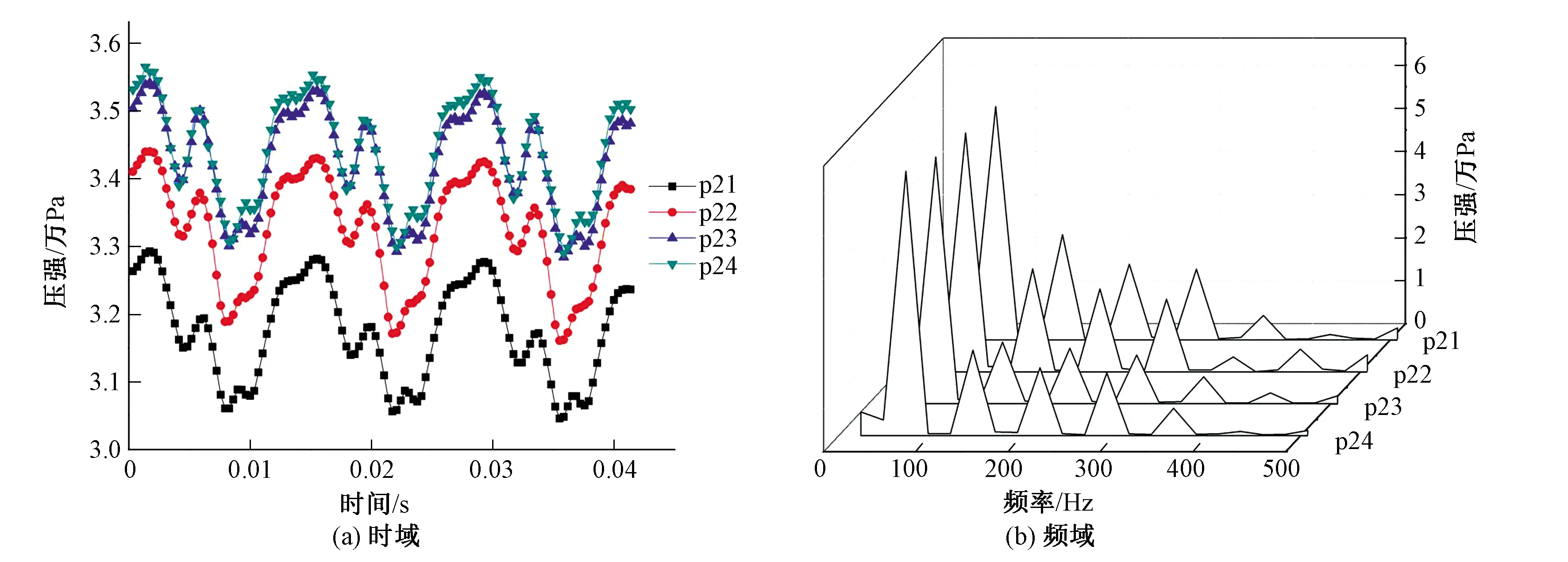
图9 叶轮出口压力脉动时域频域图
2.6.3 不同工况下的压力脉动特性
通过对3个不同工况(0.8Qopt、1.0Qopt、1.2Qopt)下4个具有代表性的监测点p11、p13、p21、p23(p11和p13分别为叶轮进口半径为80和120 mm处的监测点;p21和p23分别为叶轮出口半径为80和120 mm处的监测点)进行压力脉动监测,分析轴流泵内流量与压力脉动的关系,图10为对比分析结果。
由图10可以看出,在叶轮进口处,0.8Qopt工况下振幅最大,1.2Qopt工况下振幅最小,即振动幅值随着流量的增大而减小;叶轮出口处,0.8Qopt和1.2Qopt工况下振幅都比设计工况大,即设计工况下振动幅值最小。
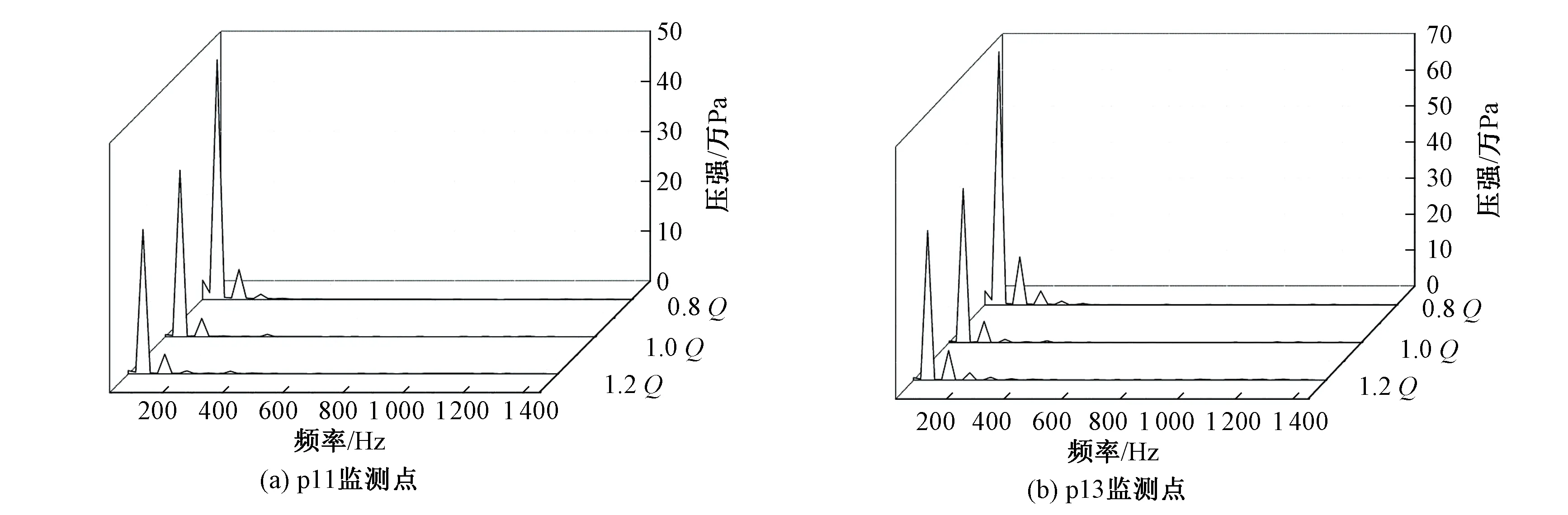
图10 不同流量下监测点频域图
3 结 论
(1)不同工况下,轴流泵叶片最大等效应力出现在工作面轮毂位置靠近进水边位置,此处易因强度不足而失效,应当适当加厚。
(2)不同工况点,叶片最大变形均出现在叶片进口边轮缘位置。
(3)叶轮的最大等效应力和最大变形均随着流量的增大而呈现较为明显的降低趋势,直到当流量大于设计工况的1.1倍时趋势才变得平缓。
(4)叶轮进出口压力脉动频率主要由叶片通过频率决定,不同流量工况下压力脉动幅值在设计工况下最小。
□
