任意弹性边界下矩形板弹性屈曲分析
2020-12-17鲍四元曹津瑞
鲍四元,曹津瑞
苏州科技大学 土木工程学院,江苏 苏州 215011
0 引 言
矩形板是实际工程中的基础性结构,被广泛应用于航空航天、土木工程、船舶结构和车辆工程等领域。矩形板构件受到接近临界载荷的压力后,有可能会发生屈曲破坏,从而造成严重的事故,甚至是极其严重的灾难。因此,人们越来越重视矩形板的屈曲分析。
自Kirchhoff 薄板理论提出以来,研究者们对薄板弯曲问题充满了兴趣,并探索得到了不同的解决方案。其中,Navier 重三角级数解理论和Levy单三角级数解[1]理论可以用来解决矩形板的弯曲问题,但这些方法主要适于解决四边简支或对边简支的矩形薄板。我国学者张福范[2]给出了多种边界条件下矩形薄板弯曲的精确解;钱伟长[3]提出了对合变换和薄板弯曲问题的多变量变分原理;胡海昌[4]基于薄板弯曲理论,提出了一个新的广义变分原理;付宝连[5]给出弹性力学混合变量的变分原理,并应用到了板结构中;姚伟岸等[6]基于辛对偶体系,给出了弹性力学的新型求解方法,可应用于薄板结构的力学问题。近年来,Wang等[7]提出采用辛迭代叠加法研究矩形薄板的屈曲问题,推导了屈曲载荷对应于非平凡解的超越方程,该方法可以解决多种非简支边界约束的薄板屈曲问题,但未处理含自由边界的薄板屈曲问题。李楠等[8]基于里兹法和复数的棣莫弗公式,研究了复合材料层合板的动力屈曲问题。汪星明等[9]基于变量分离法,给出了一种正交各向异性矩形薄板稳定问题的高效直接解法。这些文献中的方法均获得了较大成功,但实际工程结构的边界各不相同,甚至需要使用弹性边界模拟,而以上解法往往只适用于特定的边界条件,还未发现一种普适性的通用解法或结论。
在研究欧拉梁的自由振动时,Li[10]使用了一种改进傅里叶级数方法,采用该方法可以非常准确地分析出任意边界支撑条件下梁的弯曲振动特性。随后,Li[11]将改进傅里叶级数法进一步用于研究矩形板的模态特征,其每个容许函数由三角函数和任意连续函数组成,将该组函数引入以确保边缘处的残余位移函数足够平滑,并在应用Rayleigh-Ritz 法研究板自由振动问题的数值算例中证明其具有良好的收敛性和准确性。鲍四元等[12]针对不同截面形状下弹性支撑多跨梁振动,给出了一种改进傅里叶级数分析。史冬岩等[13]采用改进傅里叶级数法对正交各向异性板的位移函数进行了表达,其将薄板结构的弯曲位移函数表示为改进傅里叶级数形式,用里兹法所得到的固有频率值与有限元结果进行对比,验证了该方法的正确性。此外,王昊昊等[14]应用改进傅里叶级数研究了方形开口矩形板的振动特性;石先杰等[15]针对任意边界条件下环扇形板的静、动态特性进行了分析;薛开等[16]应用改进傅里叶级数法对Mindlin 矩形板在任意弹性边界条件下的振动特性进行了分析;Bao 等[17]给出了矩形薄板和环扇形薄板弯曲振动特性的一种统一研究方法。以上对薄板或Mindlin 板振动的研究中,均使用了位移函数展开的改进傅里叶级数形式。
针对任意弹性边界下矩形薄板的屈曲问题,本文拟采用改进傅里叶级数法和最小势能原理,得到矩形薄板结构在弹性边界条件下的屈曲特性。任意弹性边界条件[10-11,18]通过设定旋转约束弹簧和横向位移约束弹簧的刚度值来模拟,以克服以往只能求解某些特定经典边界条件板屈曲问题的缺陷,并通过算例验证本文方法的收敛性、准确性及其效率。
1 矩形薄板屈曲问题的理论模型
1.1 矩形薄板结构的物理模型
本文建立的一般弹性边界条件下受压矩形板结构的物理模型如图1 所示。矩形板长为a,宽为b,在x 方向受均布压力的作用,载荷集度为P。

图 1 弹性边界条件矩形薄板受压示意图Fig. 1 Illustration of thin rectangular plate with elastic boundary conditions

1.2 基于改进傅里叶级数模型求解
根据改进傅里叶级数[11,13]建立板结构的计算模型,设薄板弯曲位移的形式为

式(7)成立的假设条件是采用薄板的小挠度理论。
1.3 确定临界载荷
根据式(5),板结构的应变能对系数Aij求导,可得

对应矩阵特征值问题,所得特征值P 对应于板结构的临界载荷值 。基于式(12),求解矩阵特征向量,即式(11)中傅里叶系数组成的列向量A,将其代回式(1),从而可得各阶屈曲模态。
2 算 例
以下叙述中,简支边界记为S,自由边界记为F,固定边界记为C,弹性边界记为E。分别计算经典边界和含弹性边界矩形薄板的屈曲特性,其中经典边界包括CCCC,CCCS,CCSS,CCCF,CCFF和CSCF 6 种。此记法中,4 个字母代表边界条件所在边的对应次序是 x=0, y=0, x=a 和 y=b。还考察了 4 种弹性边界条件 ENENENEN(N=1, 2, 3, 4),其无量纲弹簧约束刚度系数(包括横向弹簧刚度系数和旋转约束弹簧刚度系数)均设置为10i。不同边界条件下,各种刚度系数所采用的具体值如表 1 所示。表中,kT/D 的单位为 1/m2,kR/D 的单位为1/m。
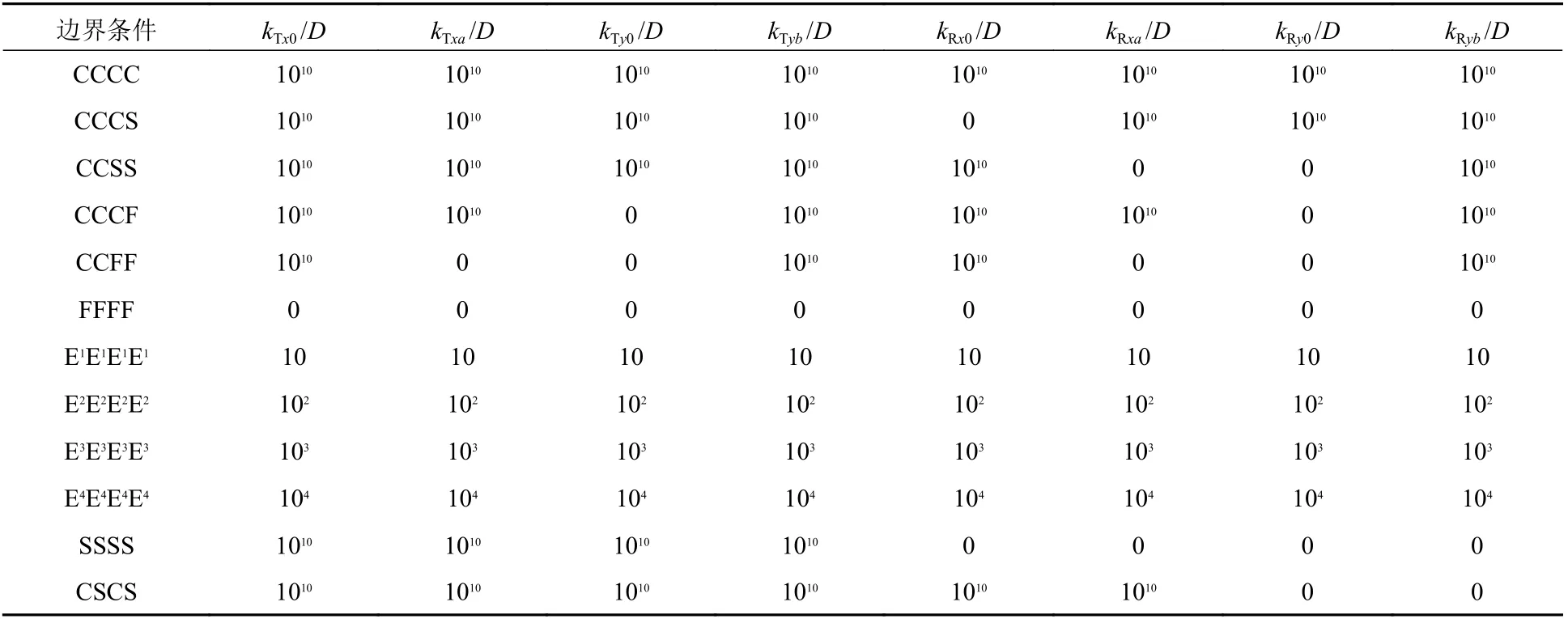
表 1 不同弹性边界条件中横向弹簧和旋转弹簧的约束刚度系数取值Table 1 The values chosen for the constrained stiffness coefficients of translational springs and rotational springs with different elastic boundary conditions
2.1 四边固支薄板
表2 所示为矩形板在四边固支(CCCC)边界条件下的前10 阶无量纲屈曲载荷系数。设定矩形板4 条边上的横向位移约束和旋转约束弹簧刚度系数均为1010。表2 示出了矩形板四边固支条件下,b/a 取值分别为 4.5,3.5,2.5,1.5和 0.5 时,矩形板前10 阶屈曲载荷系数 P¯=Pcra2/Dπ2(其中Pcr为临界屈曲载荷)与文献[7]中计算结果的比较。
由表2 可知,采用本文计算方法得到的矩形板前10 阶无量纲屈曲载荷系数与文献[7]中辛迭代叠加法的计算结果一致,可以说明,在四边固支边界条件下,利用本文方法计算所得的前10 阶无量纲屈曲载荷系数是正确的,并且具有良好的计算精度。
表3 所示为CCCC 边界条件下,在矩形板长宽比b/a=0.5 和4.5这2 种情况下,当级数截断数tm(或 tn)分别取 10,20,30 时的计算结果。从中可以看出,计算结果非常接近,说明本文方法具有良好的收敛性。
2.2 三边固支、一边简支薄板
表4 所示为矩形板在三边固支、一边简支(CCCS) 边界条件下的前10 阶无量纲屈曲载荷系数。由表4 可知,采用本文方法计算得到的矩形板前10 阶无量纲屈曲载荷系数与文献[7]中的有限元计算(FEM)结果一致。所以,在CCCS 边界条件下,同样验证了本文方法的正确性及其良好精度。

表 2 CCCC 边界矩形板前10 阶无量纲屈曲载荷系数Table 2 Dimensionless buckling parameters for thin rectangular plate with CCCC boundary conditions

表 3 CCCC 边界矩形板收敛性分析Table 3 Convergence analysis for thin rectangular plate with CCCC boundary conditions

表 4 CCCS 边界矩形板的前10 阶无量纲屈曲载荷系数Table 4 Dimensionless buckling parameters for thin rectangular plate with CCCS boundary conditions
2.3 两邻边固支、两邻边简支薄板
表5 所示为两邻边固支、两邻边简支(CCSS)边界条件下,矩形板的前10 阶无量纲屈曲载荷系数。由表5 可知,采用本文计算方法得到的矩形板前10 阶无量纲屈曲载荷系数与文献[7]中精确解结果一致,说明在该边界条件下,本文方法具有良好的计算精度。
2.4 含自由边界的薄板
本节考虑3 种含自由边界薄板的屈曲问题:三边固支、一边自由(CCCF);两邻边固支、另两边自由(CCFF)和 x =0 边简支、 y =0 边自由、 x = a和 y = b 边均固支(CSCF)。对于 CCCF,CCFF 及CSCF 边界矩形板,采用本文方法计算所得到的前10 阶无量纲屈曲载荷系数分别如表6~表8 所示。

表 5 CCSS 边界矩形板的前10 阶无量纲屈曲载荷系数Table 5 Dimensionless buckling parameters for thin rectangular plate with CCSS boundary conditions

表 7 CCFF 边界矩形板的前10 阶无量纲屈曲载荷系数Table 7 Dimensionless buckling parameters for thin rectangular plate with CCFF boundary conditions
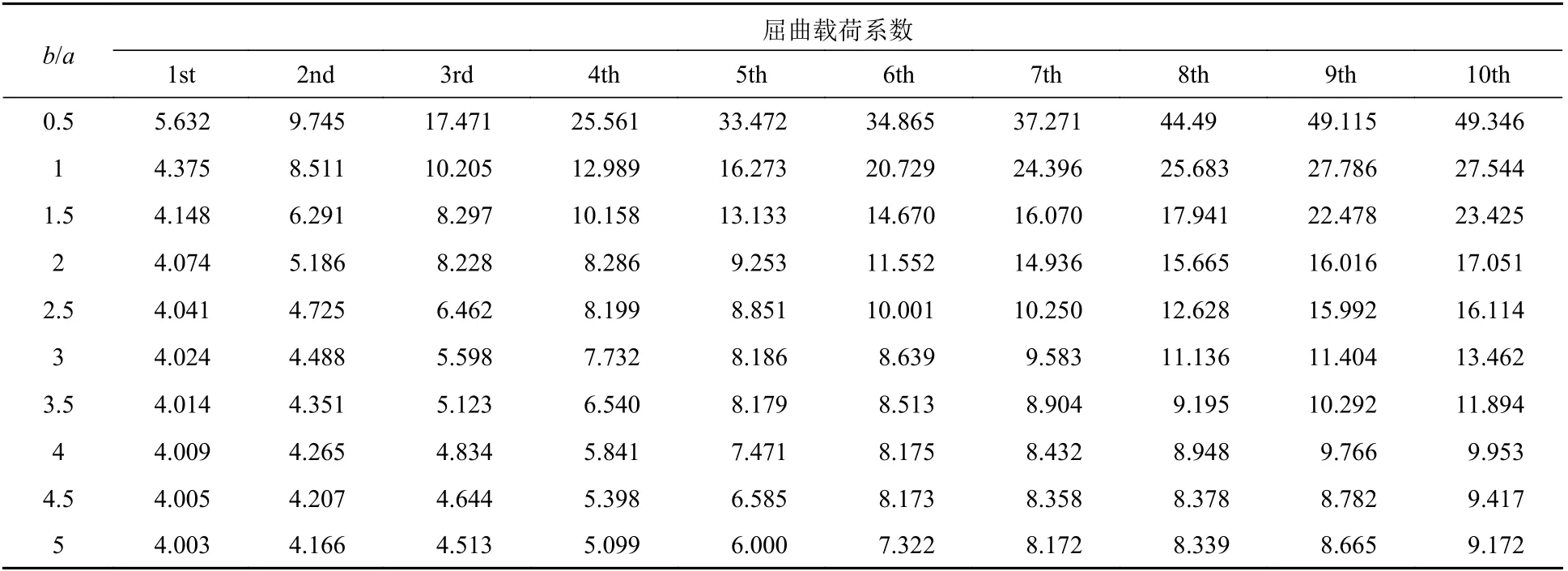
表 8 CSCF 边界矩形板的前10 阶无量纲屈曲载荷系数Table 8 Dimensionless buckling parameters for thin rectangular plate with CSCF boundary conditions
自由边界属于弱约束,相关薄板屈曲的结果较少。文献[7,19]虽然含有多种经典边界,但未包括自由边界的情况。因此,以上算例可作为标准算例,所提供的结果可为工程应用提供参考。
2.5 含弹性边界的薄板
为研究含弹性边界薄板的屈曲问题,令某方形薄板的边界条件从四边自由(FFFF)逐步过渡到四边固支(CCCC),其中含有经典边界条件SSSS,CSCS 和多种弹性边界条件(EiEiEiEi,i=1, 2, 3, 4)。
由表9 所得各阶屈曲系数的结果可知,随着边界约束的加强(按照表9 第1 列由上到下的次序),板的第1 阶屈曲载荷系数值也在逐渐增加。
另外,以长度和宽度均为1 m 的方形板,以及表9 中CSCS 边界板为例,给出该约束情况下,长、宽均为1 m 方形板前3 阶屈曲模态的等值曲面,如图2 所示(图中横、纵坐标均为方形板长、宽坐标值,单位:m)。其中,图2(b) 为反对称情形,图2(c)为对称情形。

表 9 边界约束逐渐加强时方形板的无量纲屈曲荷载系数Table 9 Dimensionless buckling parameters for a square thin plate with the boundary condition becoming stiffer


图 2 CSCS 边界方形板的前3 阶屈曲模态Fig. 2 The first three modes of a square plate with CSCS boundary
3 结 论
本文对任意弹性边界矩形薄板结构的屈曲特性进行了分析研究,得到以下主要结论:
1) 用结构的几何参数建立描述结构位移的函数关系式,即用改进傅里叶级数法表达;基于最小势能原理,得到关于位移级数展开系数的标准特征值问题,从而求得矩形板结构的临界载荷。
2) 得到矩形板的前10 阶无量纲屈曲载荷系数,与已有精确解结果或有限元结果吻合较好,充分证明了所提方法的正确性,并且具有良好的收敛性。
3) 通过改变结构四边的弹簧刚度值,有效模拟了结构在任意弹性边界条件下的屈曲问题,并给出了典型边界条件下弹簧刚度的合理取值,可为实际工程应用提供可靠依据。
