波浪作用下钻井船的共振数值计算及分析

孙雷，邓潇潇，曾智宏，刘昌凤

1 大连理工大学 船舶工程学院，辽宁 大连 116024

2 高新船舶与深海开发装备协同创新中心，上海 200240

3 大连海洋大学 海洋与土木工程学院，辽宁 大连 116023

0 引 言

随着海洋油气资源的开发，研发高效安全的海工设备迫在眉睫。在众多开采设备中，钻井船和Spar 平台的应用最为广泛。为了开采方便，这两类设备需要从甲板下放置钻井立管等施工辅助设备，故通常在船体中央设计有自上而下贯穿整个船体的矩形井，其底部为自由流动的海水，上部为自由液面，称之为月池[1]。月池内流体的运动，特别是在月池内流体共振的情况下，会对平台产生较大影响，对安全产生威胁。在合理设计和布置的情况下，月池可以屏蔽外部波浪的作用，从而保证其内部装置的作业安全。

月池内流体运动主要分为沿月池深度方向的活塞运动和月池流体液面在水平方向上的晃荡运动，如图 1 所示[2]。图中：l，b，d 分别为月池长、宽及吃水。

图 1 月池及其内部流体的活塞和晃荡运动示意图Fig. 1 Diagram of moonpool and motion of fluid piston and sloshing in moonpool

在某些共振情况下，月池内可能会发生剧烈的运动，导致潜在的安全隐患甚至设备损坏。因此，如何规避共振情况下月池结构潜在的安全隐患、最大限度发挥月池的优势，是研究人员们一直以来的研究重点[3]。

一般采用理论分析、数值计算和模型试验这3 种方法来预测共振情况下月池内流体的运动。Fukda[4]通过理论分析研究了月池内流体的运动方式，总结了月池振荡的固有周期和幅值等经验公式；Faltinsen 等[5]基于线性势流理论，研究了二维月池内流体的活塞振动；Molin[6]通过理论分析推导了月池内流体做活塞和晃荡运动时的速度势，得到了其固有频率。Kang 等[7-9]通过模型试验，探究了静水有航速和波浪无航速2 种情况下月池内流体的运动，并着重研究了月池形状和波浪条件对月池内流体运动的影响；Kristiansen 等[10]基于CFD 理论，对月池内流体的运动进行研究，提出月池开口处剪切层流的分离会影响船体的垂荡运动；李志雨[11]对计及月池的钻井船黏性流场定常和非定常CFD 模拟方法进行了研究；孙采微等[2]应用CFD 技术对一艘钻井船在波浪中的运动进行了模拟分析，发现船体的运动会增大月池内流体的活塞运动幅值；周斌[12]运用势流理论，考虑月池内、外的水流交换，建立了平台主体垂荡-月池内液体垂向运动的耦合方程；黄磊[13]基于势流理论建立月池流体运动方程，采用新的底部全开口边界条件，研究了月池内流体的自振特性及水动力特性，并建立结构垂荡-横摇及月池流体耦合运动方程，研究了月池流体对结构运动稳定性的影响。

由于试验方法耗费较大，而前人的数值计算方法普遍没有考虑航速对带月池平台的影响，本文将采用更贴合实际的波流耦合计算方法，基于势流理论的常数边界元方法，开发数值模拟计算程序（以下简称“计算程序”），对钻井船运动展开频域数值计算，验证所提数值方法的可靠性和准确性。

1 数学模型

为了研究波、流作用下船体的受力运动问题，建立如图2 所示的坐标系o-xyz。原点o 位于静水面上，设定船艏方向为x 轴正向，垂直向上为z 轴正向，指向船左舷为y 轴正向。定常来流以速度U 沿x 轴负方向传入，波浪入射角为β（迎浪时 β=180°）。

图 2 数学模型示意图Fig. 2 Diagram of mathematical model

1.1 基本假设和初边值问题

式中：nx，ny，nz是法向量在 3 个方向上的分量。

1.2 物体的载荷和运动响应

式中：ρ 为流体密度；pj中下标j=0 时为入射水压力，j=7 时为绕射水压力，j 取值为 1～6 时为 6 个自由度上的辐射水压力。

2 矩形月池共振经验和理论公式

2.1 活塞运动

式中：S 为月池内自由液面的面积。

2.2 晃荡运动

Newman[17]与Molin[6]分别推导了矩形月池N（n=1, 2, ···）阶晃荡运动共振固有频率的理论计算式。其中，Newman 给出的晃荡共振固有频率只与月池的长度有关：

2.3 考虑航速的经验公式

相比于其他人提出的月池内流体运动共振经验公式，Molin 提出的经验公式更为准确[18]，因此本文计算程序的计算结果将与Molin 经验公式计算结果进行对比。由于现有的经验公式都是针对无流速状态下的情况，而本文需要计算带航速模型，因而提出了新的经验公式：

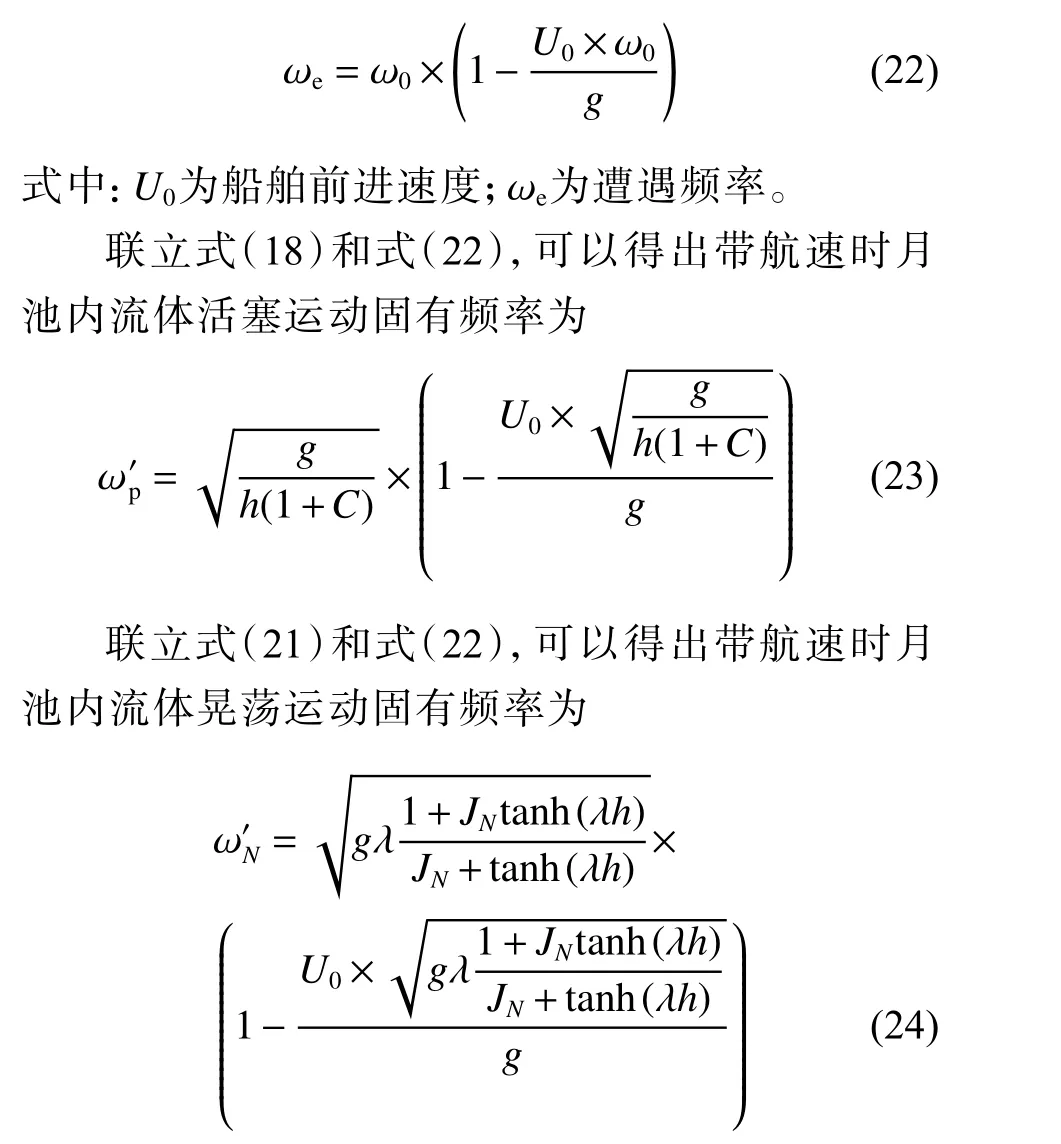
2.4 数值计算模型

本文以一艘含月池的钻井船为研究对象（图3），其主尺度参数如表1 所示。为了讨论月池对船体共振的影响，选取3 个月池尺寸进行参数化研究。在保证月池面积为256 m2的同时，设定月池长宽比 l/b 分别为 1，2，3，月池尺寸分别为 16 m×16 m，22.6 m×11.3 m，27.7 m×9.2 m。定义船舶吃水 9，7.5 ，6 m 分别为工况 1、工况 2 和工况 3，对不同月池尺寸在3 种工况下进行数值计算。

图 3 带月池钻井船模型示意图Fig. 3 Diagram of drillship model with moonpool

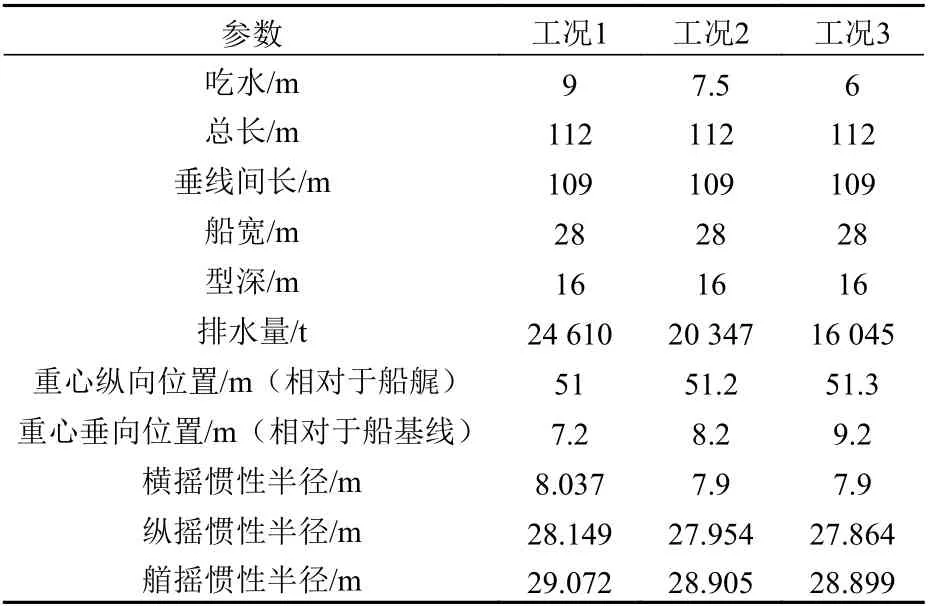
表 1 钻井船主尺度参数Table 1 Main dimension parameters of drillship

3 数值精度及有效性验证

3.1 与AQWA 软件计算结果的对比

为了验证无航速时本文计算程序的有效性，基于工况2 的参数，计算单位波幅下迎浪和横浪时，无月池及月池l/b=1 的钻井船（如图4 所示）在该工况下的升沉、横摇及纵摇的响应幅值（RAO）。将本文计算结果和船舶水动力软件AQWA 计算结果进行了对比，如图5～图6 所示。图中，f 为波浪入射频率。

图 4 月池l/b=1 的钻井船模型网格剖分示意图Fig. 4 Mesh diagram of drillship model with moonpool when l / b =1

无月池船体 180°迎浪时，在 0.115 Hz 发生纵摇共振现象，峰值较小，为 1.7 （°）/m（图 5（a））；此时，由于船长较长，可激起纵摇共振的入射波长应与其相当，此时共振频率向低频靠拢趋于极长入射波情况，且在纵摇共振点处其垂向波浪力较小，所以其升沉峰值并不明显，因此，升沉运动无明显共振（图5（b）），仍体现为在低频取得最大值，这与通常情况相符。在90°横浪作用下时，船体在0.115 Hz 发生横摇共振，峰值较大，高达 5.25 （°）/m（图 5（c））；在 0.125 Hz 处升沉峰值较大，有明显共振（图 5（d））。

在月池l/b=1 和180°迎浪下，船体纵摇与无月池情况类似，仍在0.115 Hz 发生共振，但峰值更小，仅为 1.5 （°）/m（图 6（a））；此时，有别于无月池情况，在 0.15 Hz 有明显的升沉共振（图 6（b）），证明月池对船体升沉运动有显著影响。而船体在90°横浪下，在 0.115 Hz 船体发生横摇共振，且峰值高达 6 （°）/m。另外，在 0.23 Hz附近发现由月池引起的横摇共振，但峰值较小（图6（c））；此时，在频率为0.125 Hz 处，同时发生升沉共振，峰值高达 1.4 m/m，在 0.15 Hz 处其由月池导致的升沉共振十分明显（图 6（d））。

由图5～图6 可知，采用本计算程序的计算结果与AQWA 软件的计算结果吻合良好，证明无航速情况下本文计算程序可靠。

3.2 与实验结果对比

进行有航速计算时，AQWA 软件仅仅将波浪频率用流速进行了简单的调制，使波频转化为遭遇频率直接计算，并未对波流耦合，所以AQWA计算结果不准确。利用本文计算程序解决有航速问题，并将计算结果与文献[19]中Wigley 船型的实验结果进行对比。Wigley 船型参数和网格分别如表2 和图7 所示。

参考文献[19]，本文在弗劳德数Fr=0 和Fr=0.3时进行了数值计算，计算结果与文献[19]的实验结果进行对比，如图8 所示。从图中可以看出，在Fr=0 时，升沉幅值随入射波长增加而增加，在波长船长比 λ/L 趋于 3 时，幅值趋于 0.78 m/m；纵摇幅值随入射波长的增加而平缓变化，在 λ/L=1.3 时达到最大。在 Fr=0.3 时，在 λ/L=1.2 时升沉幅值达到最大值1.3 m/m，然后降低，随后随着λ/L 的持续增加其基本保持不变；纵摇运动幅值随入射波长增加而增加，在λ/L=1.3 时达到最大，随后随着λ/L的增加逐渐减小。通过对比可以发现：本文计算程序的计算结果与实验结果吻合良好，证明本文计算程序在考虑有航速工况下的计算比较准确。

图 5 无月池钻井船RAOFig. 5 RAO of drillship without moonpool

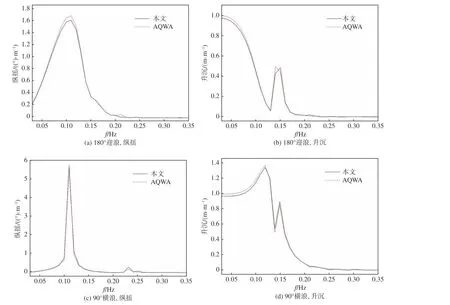
图 6 月池l/b=1 的钻井船RAOFig. 6 RAO of drillship with moonpool when l / b =1

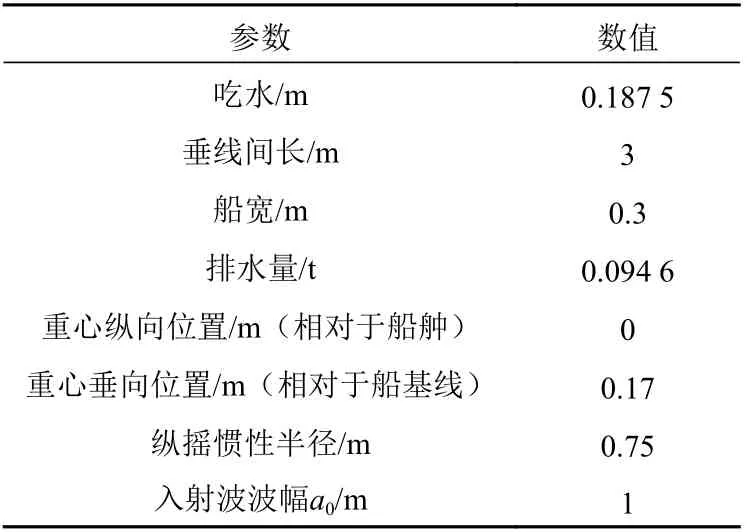
表 2 Wigley 船型参数Table 2 Main dimension parameters of Wigley ship

图 7 Wigley 船型网格Fig. 7 Mesh of Wigley ship

4 钻井船运动的参数影响分析

为了研究月池不同l/b，h 以及不同航速下钻井船的运动特性，开展了系列研究。

4.1 不同月池长宽比对钻井船运动的影响

4.1.1 对升沉的影响

通过本文计算程序，对月池不同l/b 的钻井船进行了数值计算，以6 和7.5 m吃水为代表，计算钻井船在不同波浪入射角β 的升沉运动共振频率及其对应的升沉幅值，如图9～图10所示。将本文数值计算的共振频率和Molin 给出的经验公式进行对比，如表3 所示。

由图 9～图 10可知，当月池 l/b 和 h 一定时，月池内流体活塞运动共振固有频率基本不变，与β 无关。在 β=0°和 β=180°时，钻井船升沉运动共振幅度随月池l/b 的增加而减小，当90°入射时则相反，钻井船升沉共振幅度随月池l/b 的增加而增加。即在 β=0°和 β=180°时，月池越长，升沉运动越明显；当β=90°入射时，月池越宽，升沉运动越明显；在 β=45°和 β=135°时，l/b 对钻井船升沉共振幅度影响不大。三者幅度基本相同，但l/b 的增加会使月池内流体升沉运动共振频率有细微的增加。由表3 可以看出，本文计算的共振频率与Molin经验公式计算结果吻合较好。

图 8 Wigley 船型迎浪升沉和纵摇运动Fig. 8 Heave and pitch motion of Wigley ship in head sea

4.1.2 对横摇的影响

在计算吃水为6 和7.5 m 的钻井船横摇运动共振频率及其对应的横摇幅值时，发现月池及不同l/b 对月池内流体横向晃荡运动有显著影响，如图11～图12所示。由于月池内流体的横向晃荡运动，船体会在月池内流体横向晃荡运动共振频率附近产生剧烈的横摇共振。将本文数值程序计算的横摇共振频率和Molin 给出的经验公式进行对比，如表4 所示。

由以上数据可知，月池的存在会在高频处引发船体的2 次横摇共振，随着月池l/b 的增加，共振幅度随着共振频率的增大而减小，即l/b 越小越容易激起横摇共振（波浪90°和135°入射时最明显，因为船舶的艏、艉不对称，所以45°和135°结果不同）。从表4 可以看出，本文计算的共振频率与Molin 经验公式计算结果吻合较好。

图 9 h=6 m 时钻井船的升沉运动幅值Fig. 9 Heave motion amplitude of drillship when h=6 m

图 10 h=7.5 m 时钻井船的升沉运动幅值Fig. 10 Heave motion amplitude of drillship when h =7.5 m

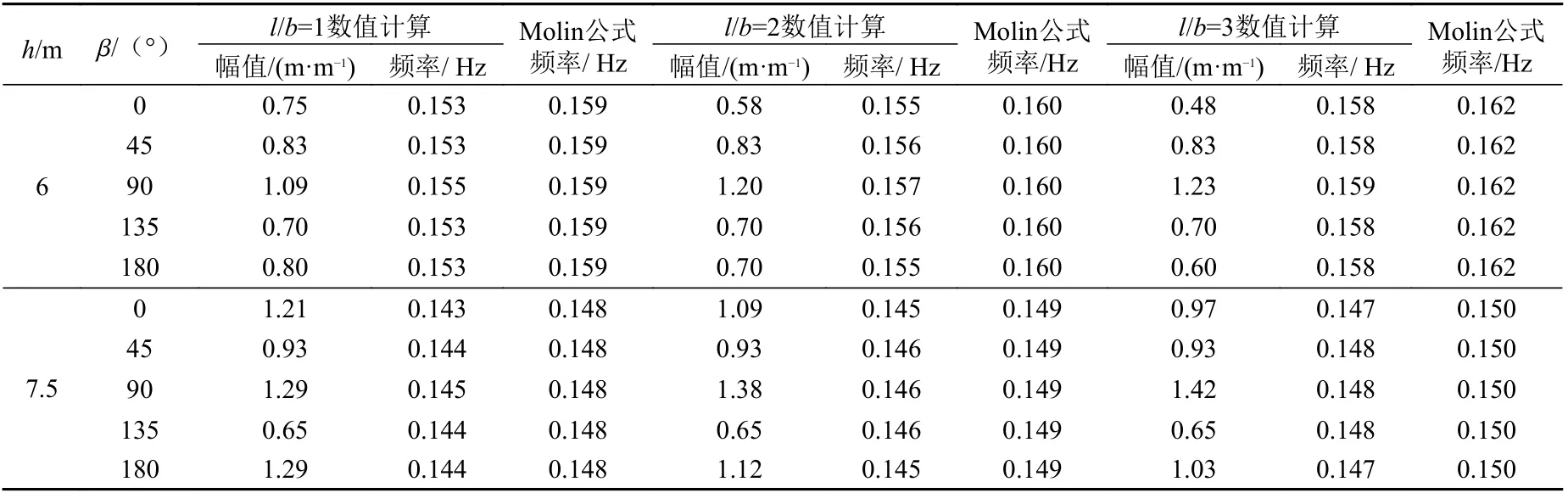
表 3 升沉运动共振频率及幅值与Molin 公式计算结果对比Table 3 Comparison of resonance frequency and amplitude of heave with results of Molin equation

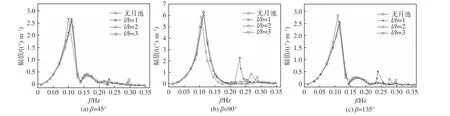
图 11 6 m 吃水时钻井船的横摇运动幅值Fig. 11 Rolling motion amplitude of drillship when h=6 m

图 12 7.5 m 吃水时钻井船横摇运动幅值Fig. 12 Rolling motion amplitude of drillship when h =7.5 m

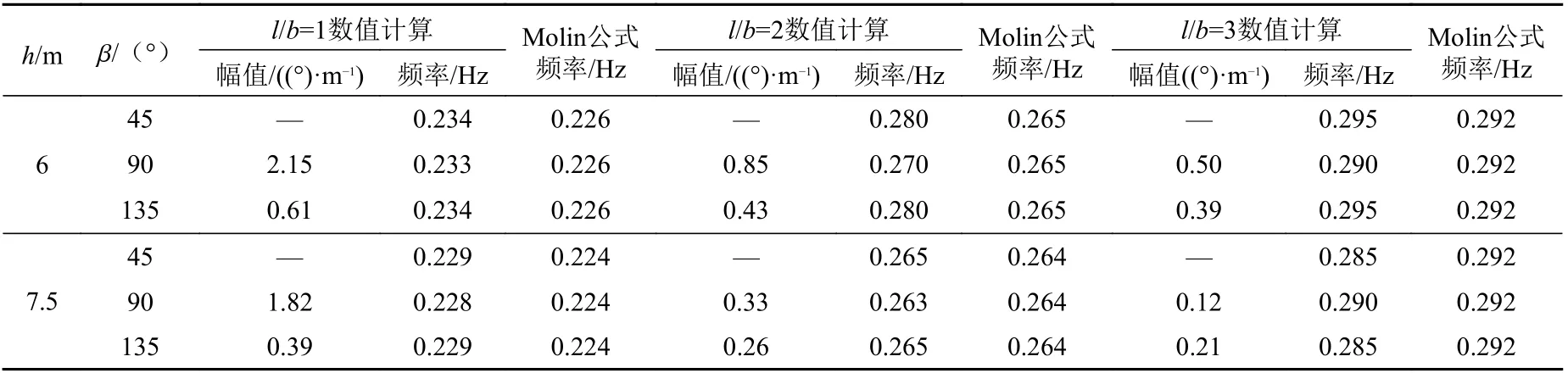
表 4 横摇运动共振频率及幅值与Molin 公式计算结果对比Table 4 Comparison of resonance frequency and amplitude of rolling motion with results of Molin equation

4.1.3 对纵摇的影响

计算吃水为6 和7.5 m 船体纵向晃荡运动有显著影响，如图13～图14 所示。由于月池内流体的纵向晃荡，船体会在月池内流体纵向晃荡的共振频率附近产生剧烈的纵摇共振。将本文计算程序的纵摇共振频率和Molin 给出的经验公式进行对比，如表5 所示。

由以上数据可知，月池的存在会在高频处引发船体2 次纵摇共振，随着月池l/b 的增加，共振幅度随着共振频率降低的而增加（吃水为7.5 m时更明显）即l/b 越大越容易激起共振。可以看出，横摇和纵摇的现象相反，当入射波纵向射入时，月池的长度l 对月池内流体影响大，当入射波横向射入时，月池的宽度b 对月池内流体影响大。从现象分析，存在一个与月池l 或b 在波浪入射方向上投影有关的“有效长度”。当“有效长度”增加时，月池内流体晃荡运动共振频率减小，共振幅度增加，也就是说，“有效长度”增加会更容易激起共振。

由表5 可以看出，本文计算的共振频率与Molin经验公式计算结果吻合较好。

4.2 吃水对钻井船运动的影响

4.2.1 对升沉的影响

以 月 池 l/b=1 和 l/b=2 为 例 ， 考 虑 不 同 β 和h 下，对钻井船升沉运动进行计算，发现吃水对月池内流体活塞运动有显著影响，计算结果如表6及图15～图16 所示。

由图15～图16 可知，当h 增加时，由月池引发的升沉共振频率降低，幅值升高，吃水增加会更容易激起共振。但β=135°时，随着吃水的增加，在频率为0.15 Hz 左右时，升沉幅值有一个明显的抬高，导致月池内流体升沉运动共振能量向低频转移，所以幅值随吃水增加而减小。

图 13 h=6 m 时钻井船的纵摇运动Fig. 13 Pitch motion of drillship when h=6 m

图 14 h=7.5 m 时钻井船的纵摇运动Fig. 14 Pitch motion of drillship when h=7.5 m

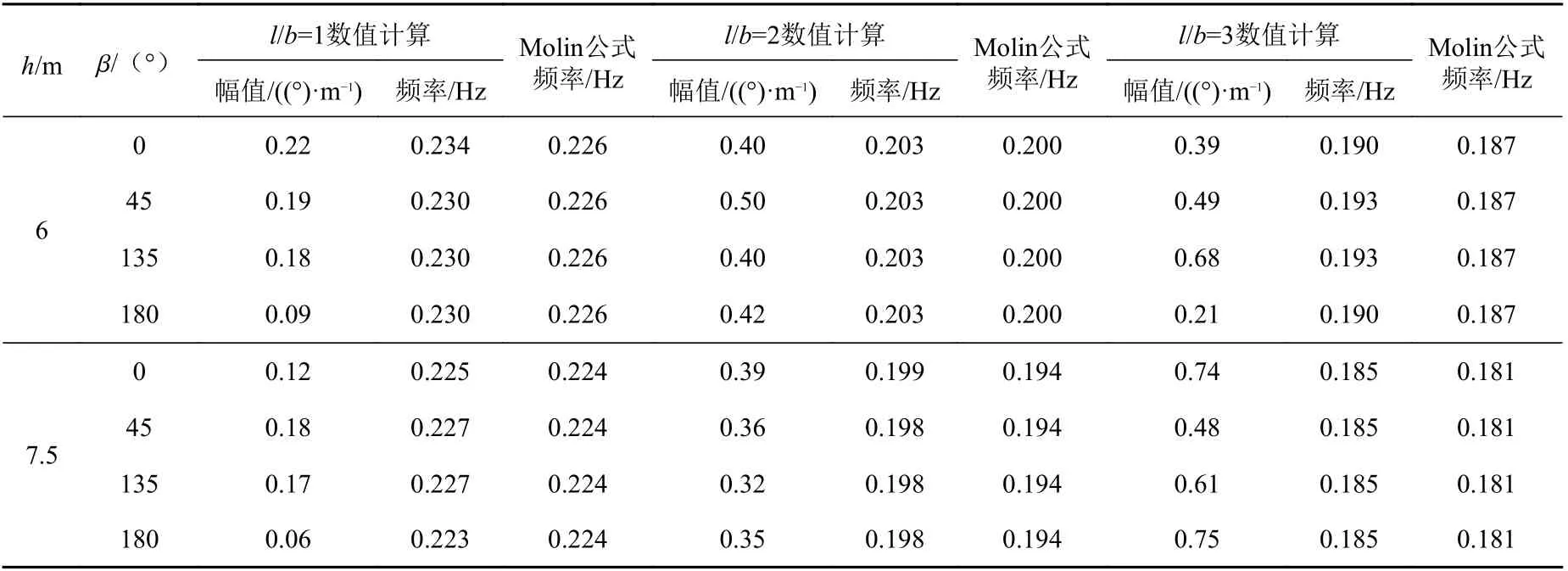
表 5 纵摇运动共振频率及幅值与Molin 公式计算结果对比Table 5 Comparison of resonance frequency and amplitude of pitch motion with results of Molin equation

表 6 升沉运动共振频率及幅值Table 6 Resonance frequency and amplitude of heave motion

图 15 月池l/b=1 时钻井船的升沉运动Fig. 15 Heave motion of drillship with moonpool when l/b=1

图 16 月池l/b=2 时钻井船的升沉运动Fig. 16 Heave motion of drillship with moonpool when l/b =2

4.2.2 对横摇的影响

以 月 池 l/b =1 和 l/b =2 为 例，考虑 不 同 β 和h 时，对钻井船横摇进行计算，发现吃水对月池内流体横向晃荡运动有显著影响，计算结果如表7及图 17～图 18 所示。

由图17～图18 可以看出，当h 增加时，由月池引发的横摇运动共振频率基本不变，幅值减小，即吃水增加会抑制横摇共振。

4.2.3 对纵摇的影响

以月池 l/b =1 和 l/b =2 为例，考虑 β 和 h 时，对钻井船的纵摇进行计算，发现吃水对月池内流体纵向晃荡有显著影响，计算结果如表8～表9 及图 19～图 20 所示。

通过对表8～表9 的分析可知，当h 增加，由月池引发的纵摇共振频率基本不变，幅值减小，即h 增加会抑制由月池引起的纵摇共振。但是与此同时h 增加会使得船体在自身共振频率下产生的纵摇增加。

4.3 航速对钻井船运动的影响

对月池l/b=3 的钻井船模型进行数值模拟，计算加入流速迎浪的情况下3 个不同吃水下钻井船的升沉和纵摇。

由图 21（a）可知，在 Fr=0.03 工况下，当吃水为 6 m 时，会产生 3 个峰值，第 1 个峰值是当频率在0.115 Hz 附近，此时是船体自身产生的共振，幅值为 1.07 m/m，相比无航速峰值（0.90 m/m）增加了 18.9%；第 2 个峰值是在频率为 0.143 Hz 时，此时是由月池内流体活塞运动共振激发的船体共振，幅值为 0.45 m/m，无航速时的共振频率为0.167 Hz，峰值为 0.81 m/m，共振频率降低了 14.4%，幅值降低了44.4%；第3 个峰值是当频率为0.168 Hz时，此时是由于航速的存在而激发的二阶共振，幅值为0.60 m/m，无航速时的二阶共振频率为0.186 Hz，峰值为 0.13 m/m，共振频率降低了 9.7%，幅值增加了362%。

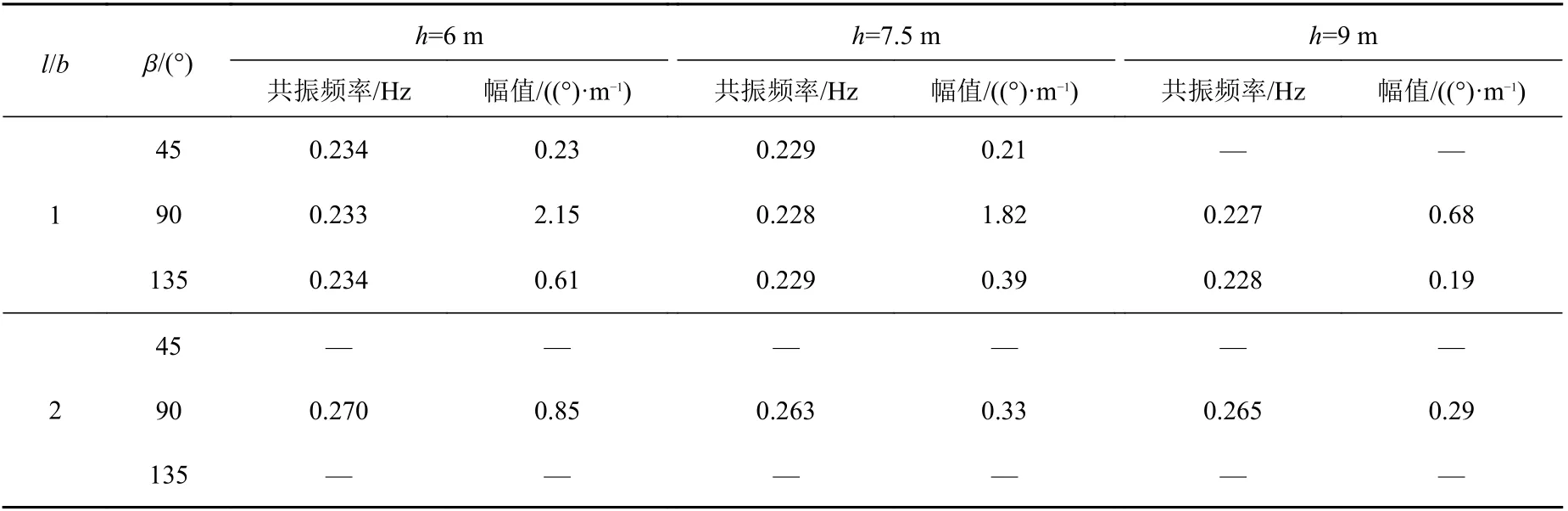
表 7 横摇运动共振频率及幅值Table 7 Resonance frequency and amplitude of rolling

图 17 月池l/b=1 时钻井船的横摇运动Fig. 17 Rolling motion amplitude of drillship with moonpool when l/b=1

图 18 月池l/b=2 时钻井船的横摇运动Fig. 18 Rolling motion of drillship with moonpool when l/b =2

表 8 月池纵摇运动共振频率及幅值Table 8 Resonance frequency and amplitude of pitch in moonpool

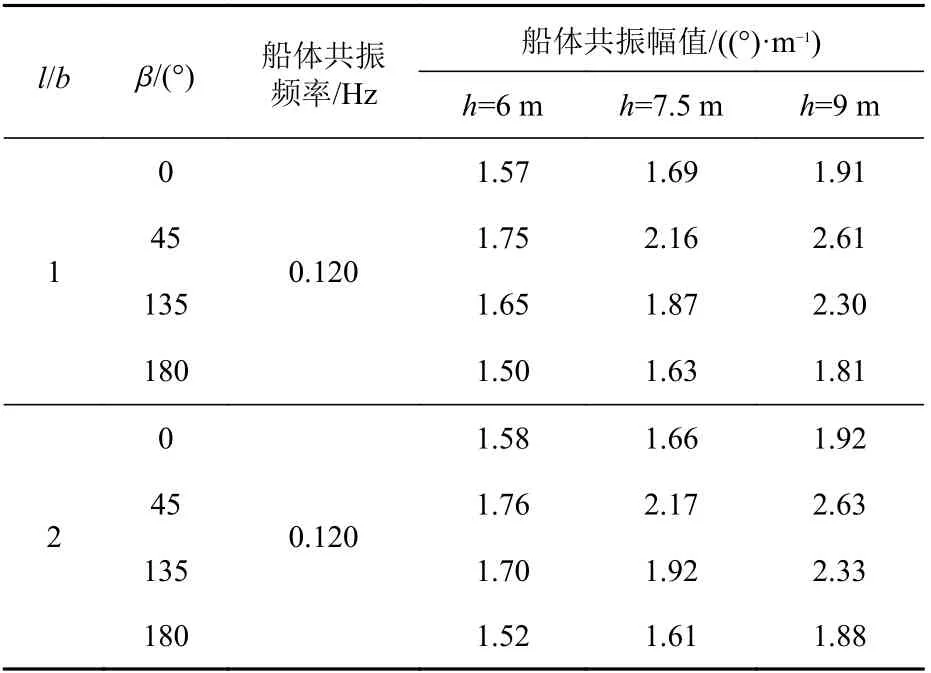
表 9 船体纵摇运动共振频率及幅值Table 9 Resonance frequency and amplitude of pitch in hull

由图 22（a）可知，在 Fr=0.03 工况下，当吃水为 6 m 时，在频率为 0.115 Hz 时，船体自身的纵摇共振幅值为 1.73 (°)/m，较无航速幅值（1.52 （°）/m）增加了13.8%；在频率为0.168 Hz 时，产生了由月池引发的船体纵摇共振，幅值为 0.89 （°）/m，相比无航速在 0.186 Hz 时幅值为 0.65 （°）/m，共振频率降低了9.7%，幅值增加了36.9%。

h=6 m 与 h=7.5 m，h=9 m 的情况相比时，船体在自身共振频率下共振幅度比无航速有明显的加剧（第 1 个峰），第 2 个峰值是当频率在 0.143 Hz附近时，此时是月池内流体活塞运动的共振，和吃水为7.5 及9 m 相比，月池内流体活塞运动共振引发的船体升沉幅度比无航速情况下的要小，这是因为月池升沉运动的能量被第1 个船体升沉运动的能量捕获。同时，航速的存在还激发了二阶升沉共振，无航速时，吃水为6 m，频率在0.168 Hz 附近，二阶升沉共振较为明显，随着吃水的增加，二阶升沉共振几乎消失，当航速存在时，可以明显地看出各个吃水下二阶升沉共振被激发，共振频率降低。

由图 21（b）可知，在 Fr=0.03 工况下，h=7.5 m时，会产生2 个峰值。第1 个峰值是当频率为0.136 Hz 时，此时是由月池内流体“活塞运动”共振激发的船体共振，幅值为1.15 m/m，无航速时的共振频率为 0.149 Hz，峰值为 1.01 m/m，共振频率降低了8.7%，幅值增加了13.9%；第2 个峰值是当频率为0.164 Hz 时，此时是由于航速的存在而激发的二阶共振，幅值为0.48 m/m，无航速时二阶共振并不可见，在航速的激发下，二阶共振可观。

图 19 月池l/b=1 时钻井船的纵摇运动Fig. 19 Pitch motion of drillship with moonpool when l/b=1

图 20 月池l/b=2 时钻井船的纵摇运动Fig. 20 Pitch motion of drillship with moonpool when l/b =2

图 21 月池l/b=3 时不同吃水下钻井船的升沉运动Fig. 21 Heave motion of drillship with moonpool in different drafts when l/b=3

图 22 月池 l/b =3 时 3 个不同吃水下钻井船的纵摇运动Fig. 22 Pitch motion of drillship with moonpool in different drafts when l/b =3

由图 22（b）可知，在 Fr=0.03 工况下，当吃水为 7.5 m 时，在频率为 0.115 Hz 时，船体自身的纵摇共振幅值为1.80 （°）/m，相比于无航速幅值（1.49 （°）/m）增加了 20.8%；在频率为 0.164 Hz 时，产生了由月池引发的船体纵摇共振，幅值为0.79 （°）/m，相比无航速在 0.186 Hz 时幅值为 0.49 （°）/m，共振频率降低了11.8%，幅值增加了61.2%。

由图 21（c）可知，在 Fr=0.03 工况下，当吃水为 9 m 时，会产生 2 个峰值，第 1 个峰值是当频率为0.121 Hz 时，此时是由月池内流体“活塞运动”共振激发的船体共振，幅值为1.55 m/m，无航速时的共振频率为 0.139 Hz，峰值为 1.42 m/m，共振频率降低了12.9%，幅值增加了9.2%；第2 个峰值是当频率为0.158 Hz 时，此时是由于航速的存在而激发的二阶共振，幅值为0.32 m/m，无航速时二阶共振并不可见，在航速的激发下，二阶共振可观。

由图 22（c）可知，在 Fr=0.03 工况下，当吃水为9 m 时，在频率为 0.115 Hz 时，船体自身的纵摇共振幅值为 2.18 （°）/m，相比于无航速幅值（1.70 （°）/m）增加了28.2%；在频率为0.158 Hz 时，产生了由月池引发的船体纵摇共振，幅值为0.48 （°）/m，相比无航速在 0.176 Hz 时幅值为 0.27 （°）/m，共振频率降低了10.2%，幅值增加了77.7%。

在吃水为 6，7，9 m 及 Fr=0.03 时，依据式（23），计算可得活塞运动共振频率分别为0.143，0.134，0.128 Hz，而本文计算的结果为 0.143，0.135，0.129 Hz；依据式（32），计算可得晃荡运动共振频率分别为0.168，0.163，0.160 Hz，而本文计算的结果为 0.168，0.163，0.160 Hz。由计算结果可知，本文给出的带航速共振频率经验公式是可靠的。

5 结 论

本文基于势流理论的常数边界元方法，通过比较有/无月池结构以及不同月池长宽比和月池吃水以及有/无航速，对带月池结构船体的运动进行了研究，得到了以下结论：

1） 月池结构的存在会使得钻井船在月池共振频率附近产生剧烈的共振，尤其对升沉运动影响更大。对于升沉运动，当“有效长度”增加时，月池内流体升沉共振幅度增加；对于晃荡运动，当“有效长度”增加时，月池内流体晃荡运动共振频率减小，共振幅度增加，也就是说，“有效长度”增加会更容易激起晃荡运动共振。

2）不同波浪入射角情况下，随着吃水的增加，月池内流体活塞运动共振频率逐渐降低，由月池共振引起的船体升沉运动峰值增加（仅135°时略有不同，峰值减小）；月池内流体晃荡运动共振频率无明显变化，由月池共振引起的船体摇摆运动峰值降低。

3） 不同波浪入射角对由月池共振引起的升沉运动影响很大，仅斜向来浪情况影响较小。因此，在钻井船工作时，应尽量调整船体使其处于斜向来浪状态，以减小由月池共振引起的升沉运动。

4） 考虑迎流情况，流速的存在会加剧船体及月池共振，并调制月池共振频率。由月池内流体活塞运动引发的船体一阶、二阶升沉运动共振幅度普遍增大（仅较浅吃水情况特殊，船体自身的共振频率会吸收月池引起的一阶共振能量而突显出来）；同时，由月池内流体晃荡运动引发的船体纵摇共振幅度增加。

从抑制共振角度出发，通过本文的计算分析可知：在波浪作用下，可以通过减小“有效长度”来抑制共振，即在保持月池面积不变的同时，调整月池的尺寸，增加垂直于波浪入射方向的月池长度可以很大程度上降低共振；同时，可以适当调整波浪入射角度，在钻井船工作时，应尽量调整船体使其处于斜向来浪状态，以减小由月池共振引起的升沉运动；吃水对于共振来说是有双面影响的，一方面吃水增加可以降低由月池引起的晃荡运动共振，但是会加剧船体本身摇动共振，同时也会加剧升沉运动共振，考虑到由于月池引起的晃荡运动共振较为微小，而升沉运动较为剧烈，所以从降低共振现象出发，可以减小吃水，但是另一方面，吃水减小也会使得平台稳性降低，因此需要以保证平台稳性为前提。

综上所述，带月池船舶在波浪作用下在升沉和摇摆运动上都会发生共振现象，引入迎流流速会调制和加剧月池共振。为了钻井船的安全考虑，建议在其未来设计中考虑来流的影响。