基于改进粒子群优化算法的船舶能量管理方案

印波，王锡淮，肖健梅

上海海事大学 物流工程学院，上海 201306

0 引 言

随着经济全球化的发展，各国货运贸易量和交易额也在不断攀升，目前，全球90%的贸易量都由船舶航运来承担[1]，作为一种经济环保的运输方式，船舶在国际交通领域有着非常重要的地位。然而，随着船舶数量的增加，行业竞争日趋激烈，营业利润空间也被逐步压缩，因此需要采用合理的船舶能量管理系统来降低运营成本。同时，船舶数量的增加及其大型化的发展趋势也导致了温室气体排放量大幅增加，从而对生态环境提出了严重挑战。因此，如何构建船舶能量管理系统，来优化控制船舶的运行成本并满足日益严格的温室气体排放标准，已成为该领域亟待解决的问题。

针对该问题，国内外学者开展了大量的研究工作。Bassama 等[2]针对混合燃料电池客船的不同工况，提出了基于运行状态的能量管理策略、等效油耗最小化策略、基于耗电量维持电荷、基于经典比例积分控制器的4 种管理方案。唐道贵[3]设计了一种包含燃料电池、蓄电池和超级电容的混合动力系统，并采用一种基于小波变换和模糊控制的智能控制策略对船舶能量系统进行了优化。Zhu 等[4]提出了一种基于模糊逻辑的燃料电池混合动力船舶能源管理策略，结果表明，该方法可以满足船舶负载需求并减少燃料消耗，同时优化混合动力模块的性能。Michalopoulos 等[5]针对船舶动力系统和电力系统分别采用了动态规划管理方案和添加轴带发电机的管理方案，在降低温室气体排放量的同时，都可以不同程度地减少船舶运行成本。宋波[6]通过对经典船型进行全线能量监测和合理控制，可以在主机和发电机均不过载的前提下保障全船动力和电力的负荷需求。徐永法等[7]基于经典船舶建立了二层冗余计算机网络体系结构，通过重载启动询问、功率限制和供电平衡等功能，实现了船舶能量分配及功率保护。目前，市场上还存在大量未改装或待淘汰的经典船型，其对船舶能量的优化受限于成本控制，且未曾考虑环境保护要求，因此，有必要对经典船型进行成本控制和温室气体排放优化管理。

本文拟采用改进粒子群优化算法（particle swarm optimization，PSO）分析经典船型的能量管理系统优化问题。根据发电机和柴油机的燃油消耗率（fuel consumption，FC）曲线极值，结合船舶动力限制及温室气体排放约束，采用改进粒子群优化策略将船舶航速、发电机组启停状态、发电机组功率等参数进行实数编码并迭代寻优，从而降低运营成本和温室气体排放量。同时，将通过对比3 种优化方案，以证明改进粒子群优化算法的可行性和有效性。

1 船舶能量管理系统的数学模型

1.1 目标函数

在满足系统约束条件的前提下，需通过船舶能量管理系统对航行速度、发电机组启停状态和发电机组运行功率分配进行优化调度[6]，其目标函数为

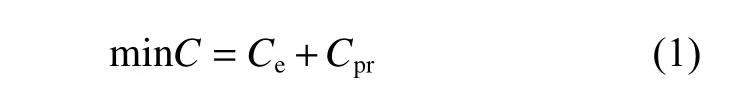
式中：C 为船舶的总运行成本，其计量单位为货币单位 monetary unit，简称 m.u.；Ce为船舶电力系统的总运行成本；Cpr为船舶推进系统的总运行成本。

1.2 船舶运行成本

对于船舶电力系统，其总运行成本Ce为

式中，a0i，a1i，a2i，a3i均为计算系数。

在船舶能量系统中，根据特定的燃料消耗SFCi即可确定成本极值，以表示单位时间内输出单位功率所需的燃料：式中：Ppr,j为已启动柴油机在ΔTj时间内的推力输出，MW；Pn,q为 n 时刻第 q 台柴油机的输出功率，MW；Pn,q'为第 q' 台已启动柴油机的额定功率，MW，其中 q' =1, 2, ···, Y，Y 为已启动的柴油机总台数。

1.3 约束条件

1.3.1 船舶发电机组的相关约束

1） 船舶发电机的功率约束。

式中，k 为计算系数，本文取值为 0.002 35。

在改变船舶航速V 以减小燃油消耗的同时，航速应满足船舶的自身属性，即船舶航速的上限和下限约束条件：式中：Lj为到达各中间港口的总航行距离，n mile；dj为船舶在各个中间港口之间的实际航行距离，n mile；τ 为各个中间港口的时间离散点集合。

1.3.5 船舶温室气体排放的标准约束

船 舶 能 效 运 营 指 数（energy efficiency operational indicator，EEOI）即单位货物周转量所产生的温室气体排放量[8]，代表了船舶在航行过程中的能耗效率，是评价其环境保护标准的一项重要指标。

式中：nP'为船舶实际乘客人数；nV'为船舶实际承载车辆数；nP为船舶额定乘客人数；nV为船舶额定承载车辆数；GT为船舶总吨位，t。

由于二氧化碳排放总量与单位时间内柴油机和发电机的燃料消耗成本成正比[9]，则有：

1.4 电力及推进力调度

船舶负载主要包括推进力负载和电力负载，且受船舶货物质量和乘客数量的影响。为了实现船舶柴油机和发电机的功率最优分配，需预测船舶的实时负载，从而准确控制柴油机和发电机的启停状态。对于给定的船舶电力负荷，可以制定发电机的启停及功率分配最优策略，并通过调整船舶航行速度来控制二氧化碳的排放量，从而满足航行及停泊时的环境保护要求。当实际负载与计算值不平衡时，采用船舶电力系统的实时最优控制方案[11]即可实现电力负载的再平衡，也可以采用负载优先启停策略[12]对船舶能量系统进行调节。

2 粒子群优化算法

粒子群优化算法（particle swarm optimizaton，PSO）是一种模仿鸟类在寻找食物过程中聚集情况的智能优化算法[13]。鸟类在寻找食物的飞行途中会彼此传递信息，因此鸟类具备分散和聚集2 种属性，虽然每只鸟的位置相对独立，但整体趋势却是向食物所在地不断聚集。在发现食物的过程中，虽然不知道食物的准确位置，但可以知道自身与食物的相对距离。通过比较每只鸟与食物之间的距离，即可得到离食物最近的一只鸟的位置，即该时间段的鸟群最优位置，也称之为粒子群的群体最优。通过信息分享，鸟群将以某种方式向群体最优的方向进行若干次靠拢，最终使绝大多数鸟类可以靠近食物所在位置，这实际上是所有可行解向最优解靠近寻优的过程。

优化问题目标函数f 的最小值为

2.1 粒子群算法寻优的基本步骤

1） 位置初始化。

粒子群优化算法是基于实数的编码寻优过程，首先需在可行解空间初始化，随机生成NP个维度为D 的可行解种群XI，即

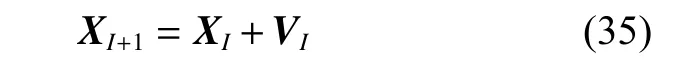
式中：VI+1为第 I +1 代种群的速度向量；w 为惯性系数；c1和 c2为学习系数；rand1和 rand2为介于[0，1]之间的随机数；ZbestI和 PbestI分别为第 I 代种群的群体最优值和个体最优值；XI+1为第I +1 代种群的位置向量。

可行解的速度和位置取值范围为：

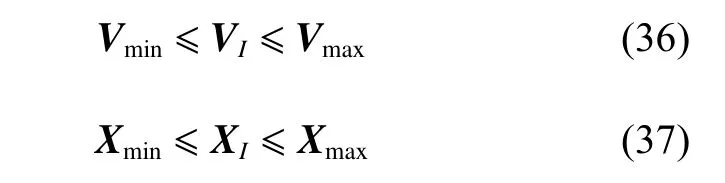
式中：Vmin和Vmax分别为粒子速度的下限和上限；Xmin和Xmax分别为粒子位置的下限和上限。

5） 适应度值更新。

根据每个粒子位置和速度的更新值，基于适应度值计算公式即可得到每个粒子适应度值的更新值。

6） 个体最优和群体最优更新。

将每一代更新之后的适应度值与个体最优和群体最优进行比较，如果当前适应度值小于此前个体最优和群体最优的适应度值，则以当前值取代此前的适应度值；否则，仍保留此前的适应度值。通过对比每一代的适应度值，即可刷新每一代个体最优和群体最优的位置，及其对应的每一代最优适应度值，从而实现个体最优和群体最优的更新。

7） 判断是否达到优化要求。

如果迭代次数达到最大迭代次数或优化结果满足输出条件，则迭代结束；否则，继续跳转至步骤4）进行迭代。

2.2 改进粒子群优化算法

粒子群算法的权重系数将在很大程度上影响粒子群的迭代效率和搜索范围[14]。标准粒子群算法一般采用固定的学习系数，或采用从大到小的线性迭代系数，但该算法不能较好地平衡全局最优和局部最优（容易陷入局部最优），且迭代速度较慢。因此，本文将采用非线性的学习系数，即初始权值较大，随着迭代次数的增加，其值将迅速减小。该自适应动态惯性权重wI的计算公式为

其中，

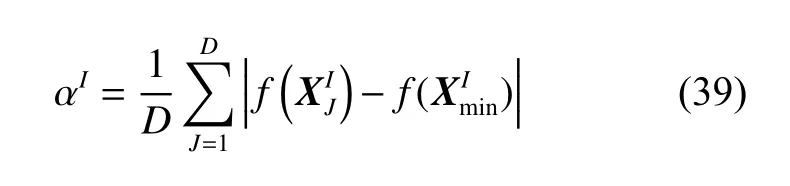
对wI进行初始化时，令第1 代w0=0.729，则α-1=3.16α0。通过每一代所有可行解的适应度值与群体最优适应度值作差求平均值，即可判断函数的平整度。如果式（39）求得的αI值较小，说明粒子的平整度较好；反之，则说明粒子的平整度较差。每一代都会产生新的适应度值，根据式（41）即可更新群体最优的适应度值，然后根据式（39）即可更新αI值，从而得到自适应动态惯性权重参数。相较于线性递减的惯性权重，本文提出的惯性权重计算规则可以有效利用当前的收敛信息来选择合适的参数，这是一种带反馈的调节方式，增强了参数选择的指向性，且相对灵活准确。

鉴于不同迭代次数中αI与αI-1的比值可能波动较大，所以本文将其作为e 的指数进行计算，从而保证每一代惯性权重参数wI的平滑性，同时将其值限定于 [0，1]范围内。当 αI/αI-1＞1 时，说明这一代粒子整体趋于发散，比值越大，则发散程度越高，wI越趋近于0，搜索步长越小；反之，当αI/αI-1＜1 时，说明这一代粒子整体趋于收敛，比值越小，则发散程度越低，wI越趋近于1，搜索步长越大。通过比较判断每一代与上一代收敛发散程度的信息采集方式，即可明确每一代的惯性权重选择情况，从而实现更好的适应程度和优化效果。

2.3 改进粒子群优化算法在船舶能量系统中的应用

步骤1：在可行解空间内初始化，随机生成NP个D 维的可行解种群，维度D 包括柴油机和发电机的启停状态、船舶航速、发电机运行功率、柴油机发电功率等11 维实数参数。

步骤2：生成种群初始速度和初始参数，包括最大迭代次数为Gmax（其中初始代数G=1）、惯性系数w、学习系数c1和c2、随机数rand1和rand2等。

步骤3：对初始化参数进行调整与约束，包括发电机和柴油机的最大/最小功率约束、爬坡约束、最大/最小启停状态约束、EEOI 约束等。

步骤4：计算初始适应度值，得出初始最优个体值和最优种群值。

步骤5：判断是否满足输出条件，即是否达到最大迭代次数或输出值满足期望值误差。如果满足，则输出结果；否则，进入步骤6。

步骤 6：根据式（34）和式（35）进行速度、位置及适应度值更新。

步骤7：将每一代更新之后的适应度值与个体最优和群体最优进行比较，如果当前适应度值小于此前个体最优和群体最优的适应度值，则以当前最新的适应度值进行取代；否则，仍保留此前的适应度值。

步骤 8：I=I+1，返回步骤 5。

3 仿真和分析

3.1 3 种仿真优化方案

根据现有的研究成果，动态规划策略[5]和差分进化（differential evolution，DE）算法[6]都适用于船舶电力系统优化。本文将采用改进粒子群优化算法来调度船舶电力系统，并与文献[5]和文献[6]中的优化结果进行对比，用以验证本文算法的可行性与优化效果。文献[5] 中：客渡船的总吨位为 48 750 t，最高航速为 23.5 kn，最大载客量 为1 800 人次，最大车载量为 500 辆，航行过程中二氧化碳排放量约束 EEOI1=21 g/(t·kn)，船舶进港停泊时二氧化碳排放量约束 EEOI2=120 g/(t·h)。为了与文献[5]中动态规划策略的优化结果进行对比，本文将采用相同的参数，包括船舶自身相关参数、乘客量及车辆数量、航行距离、船舶与港口之间的距离等。

在电力输出和推进力输出方面，本文为该船舶配置了3 台发电机和2 台柴油机，每台柴油机都通过轴连接至1 台推动装置，具体参数如表1所示[5]，其中P 为发电机或柴油机的单位时间输出功率。

本文设定模拟航线的总长度为 307.744 2 n mile，航线中间会停经3 个港口，航行过程中船舶的实际载客数、实际货物量和负载因数如表2 所示。

本文拟采用3 种优化方案，具体如下：

1） 方案 1：船舶配置 3 台发电机和 2 台柴油机，不采用最佳功率调度和推进力优化分配，不对EEOI 进行限制约束。对于电力负载和推进力负载，发电机和柴油机都采用均匀分配的方式。

2） 方案 2：船舶配置 3 台发电机和 2 台柴油机，采用最佳功率调度，不采用推进力优化分配，不对EEOI 进行限制约束。

3） 方案 3：船舶配置 3 台发电机和 2 台柴油机，采用最佳功率调度和推进力优化分配，对EEOI进行限制约束。

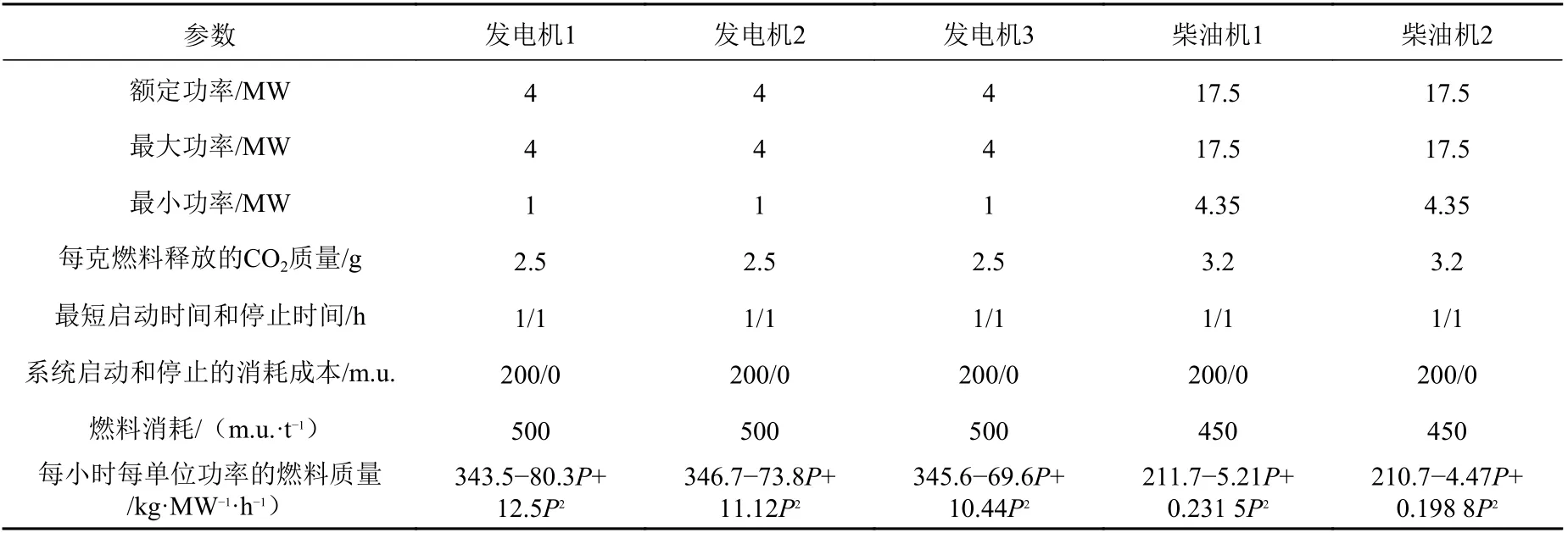
表 1 船舶动力系统数据Table 1 Data of ship power system

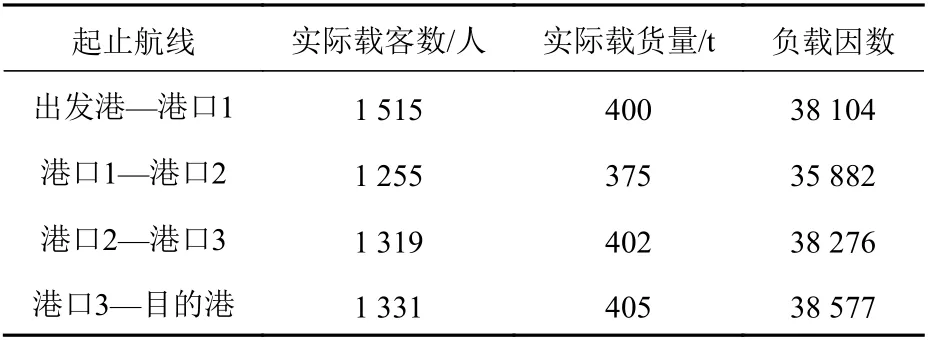
表 2 船舶满载度数据Table 2 Data for ship fullness

3.2 仿真结果与分析

对于给定的船舶总负载、电力负载、推进力负载和航速，即可绘制船舶相关参数的曲线图，如图1 所示。设定船舶的航行时间分为36 个时间段（ΔT1～ΔT36，下文简称 T1～T36，图中则直接采用数字进行标示），每个时间段的间隔均为0.5 h。

方案1 和方案2 设定了航速不变，因此相应的船舶推进力负载也保持不变；在环保限制EEOI方面，方案1 和方案2 均未采取相关约束进行优化。但方案2 的船舶发电机采用了电功率优化分配策略，可以在电力负载已知的情况下基于改进粒子群优化算法进行功率预分配，从而降低电力运行成本，而方案1 仍采用了均匀分配电力负载的传统方式。方案3 在方案2 的基础上，进一步采用改进粒子群优化算法对船舶航速进行调整，用以优化船舶推进力负载，同时满足环保约束EEOI 条件。

3 种方案的优化对比情况如表3 所示。

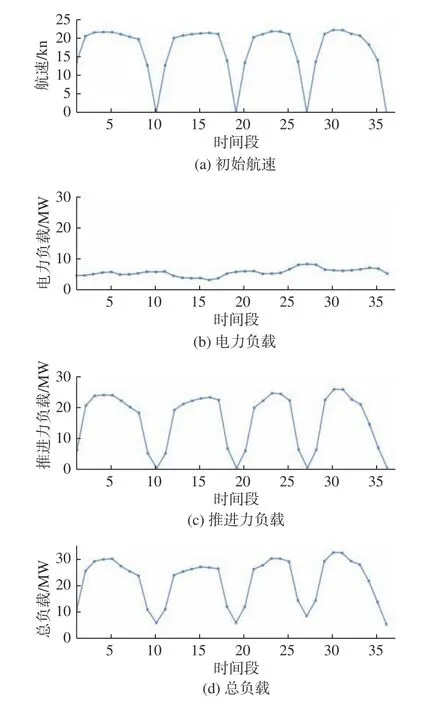
图 1 船舶的初始航速、电力负载、推进力负载及总负载曲线图Fig. 1 Curve chart of initial ship speed, power load, propulsion load and total load of the ship

图2 是3 种方案在T1～T36时间段的船舶航速对比示意图。由图2 可知：未使用推进力优化策略的方案1 和方案2 的航速基本一致；方案3 采用了推进力优化策略，其在到达港口和离开港口时的航速更高，而正常航行时的航速则明显降低，停泊时航速为0。图3 是3 种方案在T1～T36时间段的船舶推进力负载对比示意图。由图3 可知：船舶在T10，T19，T27，T36时刻的航速为 0，推进力为 0；与方案 1 和方案2 相比，方案3 在接近港口和离开港口时的推进力更高，而正常航行时的推进力负载则明显降低。

图4 是3 种方案在T1～T36时间段的船舶运行成本对比示意图。由图4 可知：受船舶发电机和柴油机运行功率和启停工况的直接影响，燃料成本曲线基本与总负载正相关；与方案1 和方案2相比，方案3 经优化之后的总成本明显降低，这体现了改进粒子群优化算法的可行性。

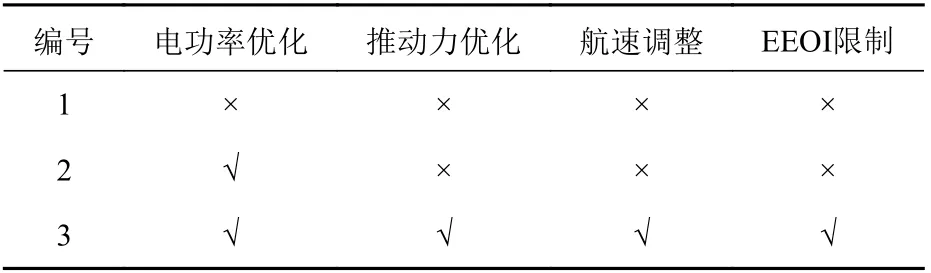
表 3 3 种方案的优化对比结果Table 3 Optimization comparison results of three schemes

图 2 船舶航速对比图Fig. 2 Comparison of sailing speed

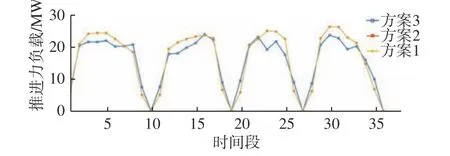
图 3 船舶推进力负载对比图Fig. 3 Comparison of ship propulsion load

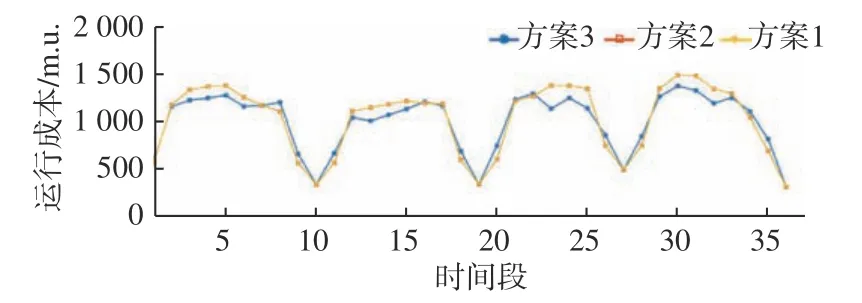
图 4 船舶运行成本对比图Fig. 4 Comparison of ship operating costs

图5 是3 种方案在T1～T36时间段的船舶环保约束EEOI 值对比示意图。由于船舶在T10，T19，T27，T36时刻处于泊位，航速为0，所以采用EEOI2限值，其余航行时刻则采用EEOI1限值。为便于图形对比，将EEOI2值缩小1/10 进行处理。由图5可知，与方案1 和方案2 相比，方案3 采取条件约束之后的限值可以满足环保标准要求。

图6 所示为3 种方案的3 台发电机和2 台柴油机在36 个时间段内的启停状态及输出功率（假设所有发电机和柴油机已提前预热运行0.5 h）。

由图6（a）可知，对于未经优化的方案1 而言，在电力负载（或推进力负载）低于单台发电机（或柴油机）最大功率的情况下，可以优先使用1 台发电机（柴油机），例如由发电机1 负责提供电力负载；反之，则均匀分配负载，即对每台启动的发电机（或柴油机）输出功率进行均分。在船舶从一个港口到达下一个港口的时间段内（T1～T10，T11～T19，T20～T27，T28～T36），船舶总负载呈现了中间高两端低的发展趋势，这与实船工况相符。

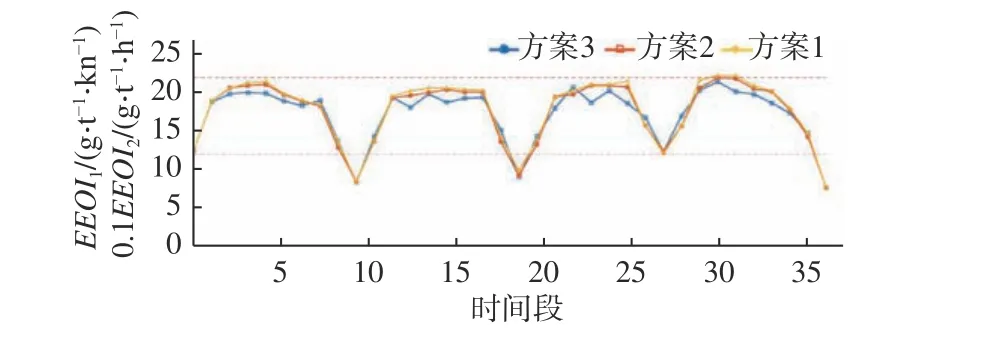
图 5 船舶 EEOI 对比Fig. 5 Comparison of ship EEOI

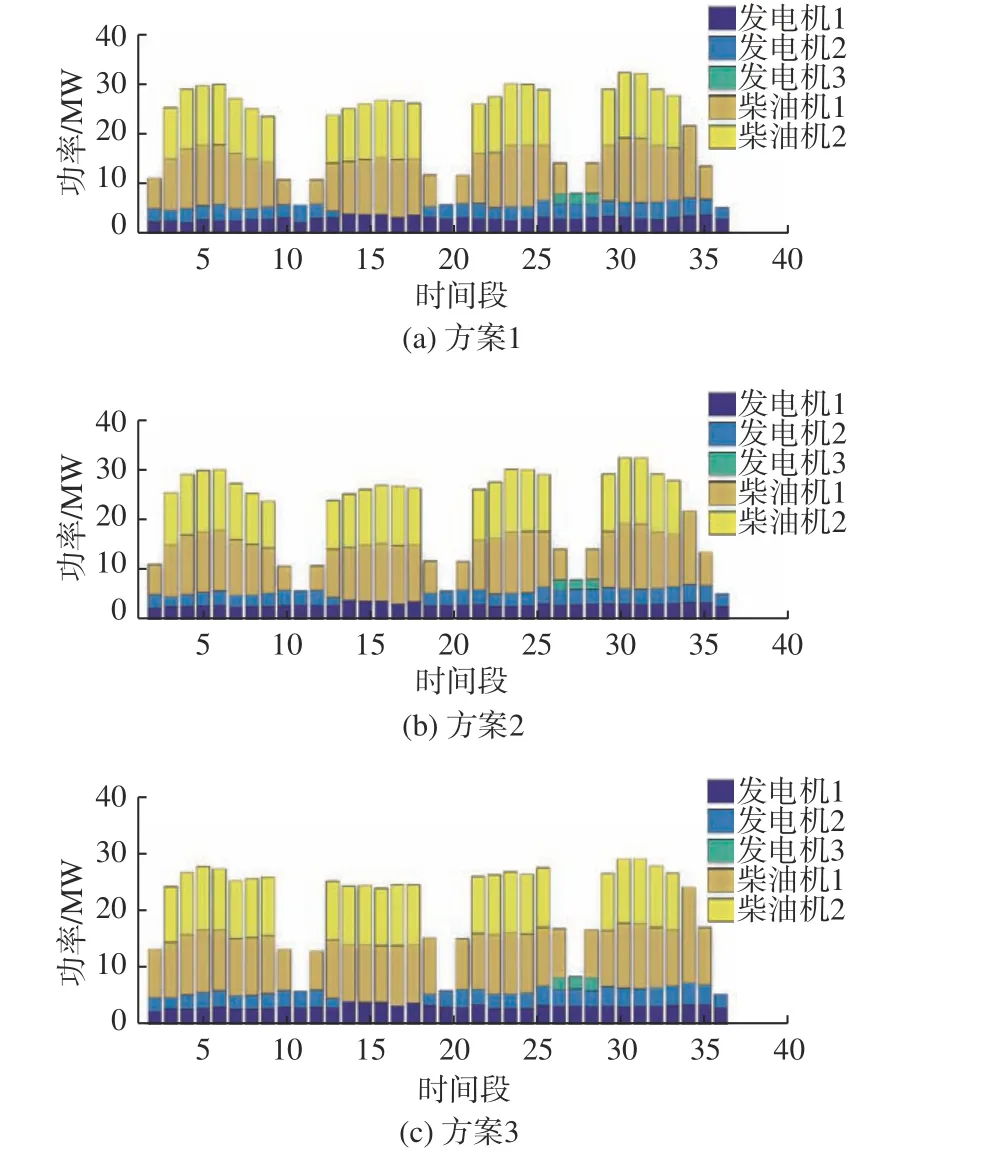
图 6 3 种方案下船舶发电机和柴油机的输出功率图Fig. 6 Power output of ship generator and diesel engine in three schemes

图6（b）中，方案2 的推进力负载和总负载情况与方案1 相似，但经电力负载优化分配之后，其整体表现更为平稳，可以在满足电力负载的前提下同时节约发电机的成本消耗。

由图 6（c）可知，与方案 1 和方案 2 相比，方案3 的推进力负载变化较大，通过推进力负载在各时间段的增减分配，最终使总负载基本维持在较稳定的水平。

根据仿真结果： 方案1 的运行成本为37 022.75 m.u.；采用电功率优化策略的方案 2 的运行成本为 36 993.27 m.u.，降低了 0.079 6%；采用电功率及推进力优化策略的方案3 的运行成本为 35 851.25 m.u.，降低了 3.164 2%，且方案 3 可以满足EEOI 环保要求。因此，改进粒子群优化算法可以降低船舶的运行成本并满足环保要求。

3.3 与现有文献的对比结果

在相同的船舶参数和条件约束下，采用动态规划策略[5]和差分进化算法[6]时，方案2 比方案1分别节约了0.05% 和0.06% 的成本，方案3 比方案1 分别节约了2.02% 和2.90% 成本；采用改进粒子群优化算法时，方案2 比方案1 节约了0.079 6%的成本，方案3 比方案1 节约了3.164 2%的成本。由此可见，在满足各项约束条件和环保要求的情况下，基于改进粒子群优化算法策略的船舶能量管理方案具有更好的经济性。

图7 所示为改进粒子群优化算法与差分进化算法[6]的运行成本收敛结果对比，可以看出：改进粒子群优化算法在迭代50 次左右就基本实现了全局最优，且迭代效果更优，而差分进化算法则需要迭代150 次，由此可见，改进粒子群优化算法具备更优的收敛性和稳定性。

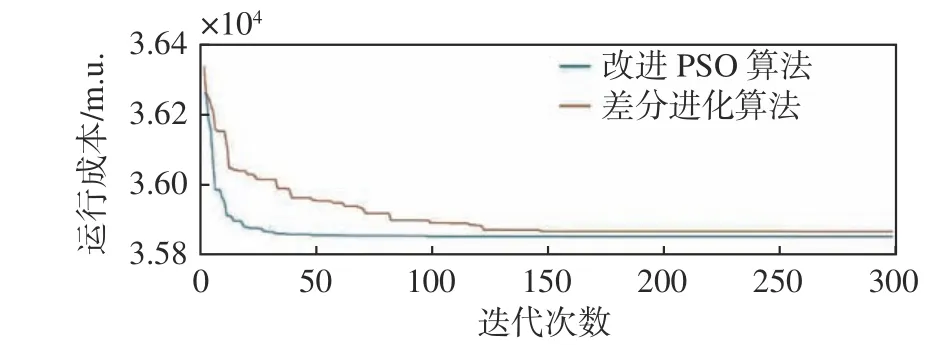
图 7 改进粒子群优化算法与差分进化算法的运行成本收敛情况Fig. 7 Operating cost convergence of improved PSO and DE

4 结 语

在满足船舶各项基本约束条件和环保要求的前提下，本文提出了一种更具经济性和环保性的船舶能量管理方案。通过将发电机和柴油机的启停状态和运行功率及航速进行实数编码，并采用改进粒子群优化算法进行迭代寻优，不仅降低了运行成本，还减少了船舶航行过程中二氧化碳的排放量。与动态规划策略和差分进化策略相比，改进粒子群优化算法可以在更短的优化时间内找到更优解，故其具有较好的响应速度和优化稳定性。本文已对船舶的电力系统和推进系统进行了优化，在后续研究中将进一步引入轴带发电机，考虑将电力系统和机械系统进行耦合分析。