一种飞行甲板设计要素的论证方法

杨放青，朱永安，赵守君*

1 江南造船（集团）有限责任公司，上海 201913

2 国防科技工业舰船总段建造与装配技术创新中心，上海 201913

0 引 言

飞行甲板设计是航空母舰（以下简称“航母”）总体设计的重要内容。航母飞行甲板作为一种非对称、不规则的多边形，其上功能分区及部分航空保障作业甲板资源的布置也存在重叠和不对称性[1-2]。因此，飞行甲板总布置设计与其他水面舰船或者民用船舶的上甲板设计存在很大区别。作为航母上重要的航空保障作业场所，飞行甲板设计问题的复杂程度更高、涉及到的主要设计要素更多[3-5]。目前，设计人员已开始将各类智能优化算法应用于包括航母在内的各型舰船的总体设计中[2,6]，对提升舰船研制的科学性并提高设计效率具有显著作用。然而，通常单目标或多目标优化算法主要还是应用于局部结构或者局部布置设计问题，若需将飞行甲板作为一个整体来考虑其主尺度要素设计问题，传统的优化方法在应用时，尤其是在建立目标函数的过程中较为复杂[7]。为解决这一问题，本文将从飞行甲板主尺度要素与航母舰体主尺度要素间的关系入手，采用支持向量机回归（support vector machine regression，SVR）算法[8-9]对这种关系进行回归分析，以期建立一种通过舰体主尺度来论证飞行甲板主尺度要素的方法，并根据这种方法，以部分国外典型航母的舰体及飞行甲板相关设计参数作为机器学习样本集，对计算误差进行分析，以验证该方法的回归精度和适用性。

1 研究思路

由于飞行甲板主尺度要素包括多方面的设计参数，因此需简要分析选取的各要素对飞行甲板整体性能表现的影响。同时，整理汇总了国外典型大、中型航母的飞行甲板及舰体主尺度要素数据，以作为论证飞行甲板主尺度要素回归模型的数据样本。需要注意的是，所选取的航母可以分为大型和中型2 类，两者除了在尺度和排水量上存在明显差异外，在飞行甲板布置设计时主要考虑的问题及限制因素也有所不同。

1.1 飞行甲板主要设计要素概述

选取的设计对象，即飞行甲板设计要素包括：飞行甲板长Lfd、飞行甲板宽Wfd、斜角甲板长Lad、斜角甲板宽Wad、斜角甲板角度α、斜角甲板横向位置tfd、弹射器或独立起飞跑道数量Nc共7 个设计要素。国外典型大、中型航母的飞行甲板设计要素如表1 所示。

表 1 国外典型大中型航母飞行甲板设计要素Table 1 Flight deck's design parameters of typical foreign large and middle aircraft carriers

1.2 舰体主尺度要素的选取

作为设计输入量的航母舰体主尺度要素包括：设计水线长Lw、设计水线宽Ww、设计吃水Td、型深Dd、标准排水量DispS、满载排水量DispF、试航航速VT、推进功率PP共8 个变量。国外典型大、中型航母的舰体主尺度要素如表2 所示。

确定了研究样本数据后，通过引入SVR 算法并结合模拟退火算法（SA）进行训练，即可构建飞行甲板主要设计要素的回归模型。

2 基于SVR 的飞行甲板主要设计要素预测模型

2.1 支持向量机原理

本文大、中型航母的样本数量有限，基于数理统计理论的传统回归分析方法需要依赖大量的样本数据作为分析基础，因此采用该方法难以取得较好的回归效果。而支持向量机是一种基于统计学习理论（statistical learning theory，STL）[10-12]中结构风险最小化（SRM）原则的机器学习方法，与以人工神经网络（ANN）方法为代表的基于经验风险最小化（ERM）原则的机器学习方法相比，具有严格的数学理论支持，在小样本、高维度、高非线性回归问题上具有更好的性能表现，因而也能够克服传统回归分析方法的不足。因此，考虑到当代典型大、中型航母型号有限、设计要素多的具体情况，SVR 算法非常适于构建本文中飞行甲板主要设计要素预测模型。

表 2 国外典型大中型航母舰体主尺度要素Table 2 The main dimensional factors of the hulls of typical foreign large and middle aircraft carriers

式中：常数C＞0，为均衡因子；ε 为不敏感带宽度。

进而，通过构造拉格朗日方程并求解极值点，可得到式(3) 的对偶优化问题，其求解极小值问题可表示为：

根据 KKT（Karush-Kuhn-Tucker）条件，式 (6)在最优解处有

2.2 计算参数的优化

2.2.1 核函数的选取

由于支持向量机是利用核函数来实现将样本数据映射至高维特征空间的，因此核函数的选取也是SVR 建模中的一个重要部分。目前，常用的核函数形式包括多项式核函数、RBF 核函数、Sigmoid 核函数等。本文建模选择的是RBF 核函数，又称为径向基核函数，如式(9)所示。其优点是能提高训练集中与检验样本更接近的训练样本的重要程度，增强这些样本对回归结果的影响程度，进而提高回归精度。

式中，σ 为 RBF 核函数的参数。

由上式可知，当2 个样本xi与xj较相似时，其核函数值越大，越接近于1，因而在SVR 表达式中与检验样本更接近的训练样本所占权重也更大。

2.2.2 回归参数优化模型

由2.2.1 节的分析可知，当前建立的SVR 模型中有 3 个参数（C，ε，σ）需要确定，其取值将影响最终回归模型的性能，即对飞行甲板主要设计要素的预报精度。为此，需要对参数进行优化，以提高SVR 的性能。

因此，其能够以一定的概率接受次优解，从而确保算法的全局搜索能力。

其中，t 开始时取较大的值，而每一轮内循环结束后t 都将减小，直至最终满足某个终止条件，算法即停止迭代，输出此时的外循环最优解即为最终优化结果。因此，算法的收敛速度由L 以及t 的衰减函数决定。

综上，整个SVR 的训练和推广性能检验过程如图1 所示，通过采用SA 算法对基于某训练集的回归模型参数进行优化，然后针对训练集以外的某检验样本计算其回归误差。需要说明的是，由于每一次计算都只能针对某个特定的飞行甲板设计要素的回归模型参数进行优化，因此需要对7 个所选取的飞行甲板设计要素分别建立SA 优化模型并求解，以确保最终每一个设计要素预报值都能取到最小误差估计。

3 基于典型航母样本数据的论证效果分析

为了分析基于支持向量机的飞行甲板主要设计要素回归模型的预报能力，选取美国海军“肯尼迪”号(CV-67)航母相关要素作为检验样本，其他航母作为训练集来对回归模型进行训练，并根据2.2 节中的SA 算法对回归参数进行优化。其中参数设置为：L=500，初始温度t0=0.01，终态温度 tf=0.000 001，温度衰减函数为 tu+1=tu·0.95。

图 1 SVR 模型参数优化与检验Fig. 1 Parameters' optimization and inspection of the support vector machine regression model

由于此“肯尼迪”号是目前为止美国海军建成的最后一艘大型常规动力航母，也是目前设计水平最高的常规动力航母，设计建造于20 世纪60 年代，其飞行甲板设计较“小鹰”级的前3 艘做了较为明显的改进。美国海军从“小鹰”/“企业”级发展到“尼米兹”级过程中，“肯尼迪”号航母起到了承上启下的作用，在大型航母中非常具有代表性，因此选取该航母作为检验样本。

表3 所示为采用SA 算法 SVR 模型训练过程进行优化而得到的相应参数以及对检验样本的预报结果与误差。将部分数据绘制成柱状图，其中，图2 为实际值和预报值的对比，图3 为训练集LOO 误差和检验样本预报误差的对比。

从表3 以及图2、图3 中的数据可以看出，采用SA 算法优化后的SVR 模型对飞行甲板各设计要素的预报精度，多数设计要素都能获得较为满意的预报精度。其中，序号 1，2，3，4，7 对应设计要素预报值与“肯尼迪”号实际值的误差均控制在5%以内，基本具备工程实际应用的潜力；剩下的2 个飞行甲板设计要素，也即斜角甲板度数、斜角甲板横向位置的预报结果则不太理想，误差均超过了10%，甚至接近30%。

检验样本预报误差直接反映了该飞行甲板设计要素与所选取作为回归模型中输入量的舰体主尺度要素的关联性，而训练集LOO 误差则表示了该设计要素规律性强弱和各训练样本的离散程度，尽管图3 中对于部分设计要素来说，两者在数值上会存在较大的差异，但从整体上看两者的变化规律是一致的，例如训练集LOO 误差最大的序号5，6 对应的设计要素的检验样本预报误差，显著大于其他设计要素的预报误差。

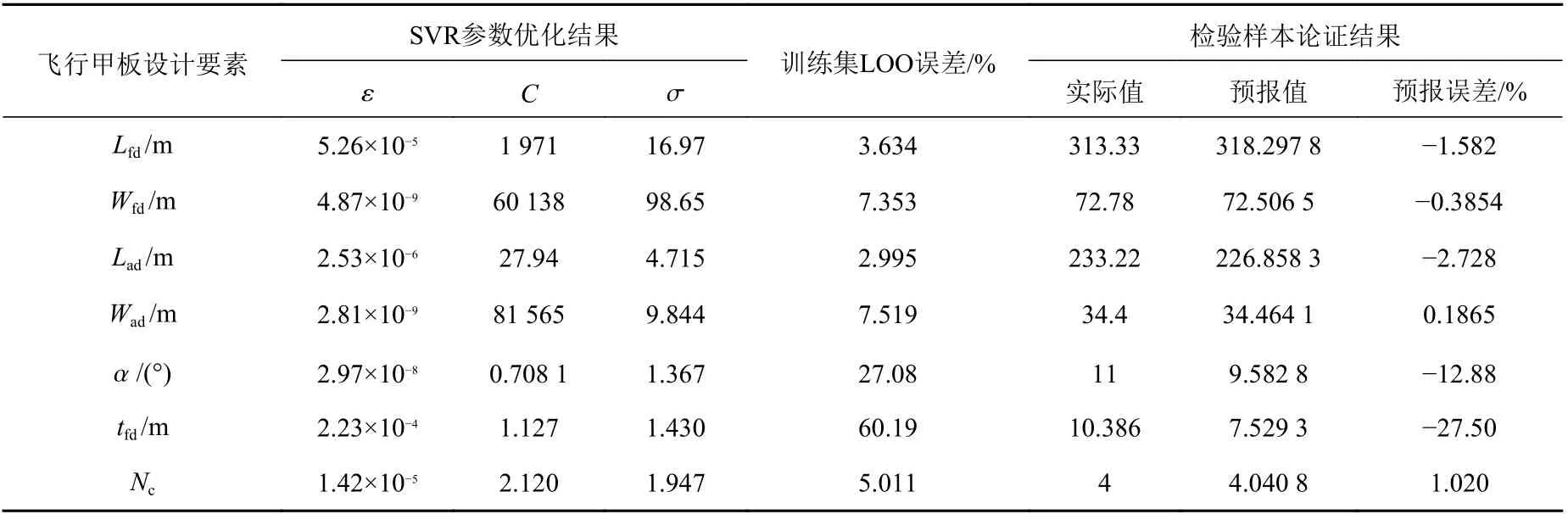
表 3 SVR 论证结果Table 3 The demonstration results of the SVR algorithm

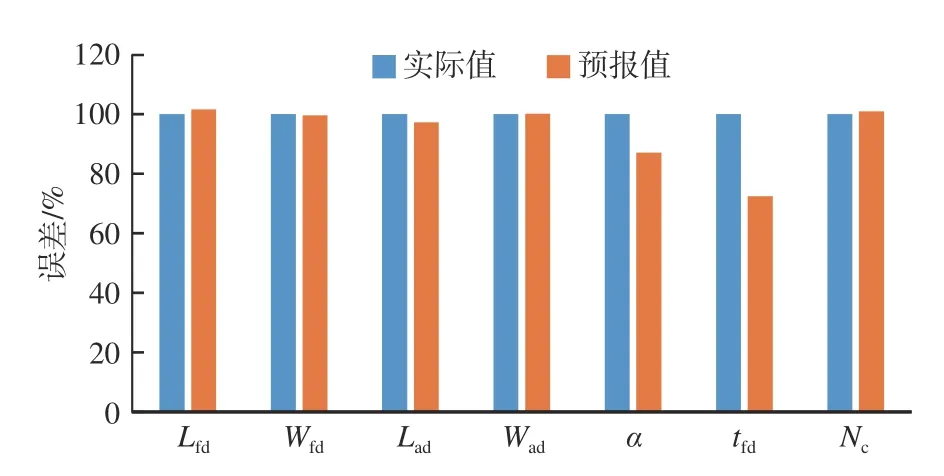
图 2 检验样本预报值与实际值的误差对比Fig. 2 Comparison between the inspecting sample's predicted values and actual values

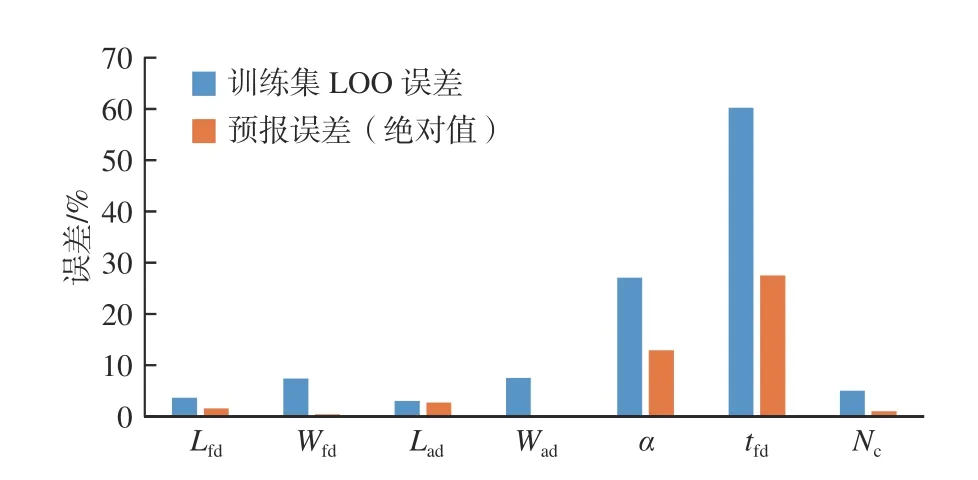
图 3 训练集LOO 误差与检验样本预报的误差对比Fig. 3 Comparison between the LOO errors and the inspecting sample's predicted errors

序号1～4 都是与飞行甲板主尺度直接相关的设计要素，其预报精度高，表明舰体主尺度等舰体设计要素与飞行甲板主尺度存在很大的联系，更大的舰体通常能够布置更长和更宽的飞行甲板，并且其斜角甲板的尺度也会相应增大。虽然不同型号的大型航母在主尺度和排水量等舰体设计要素上有所差别，但其独立起飞跑道数的差别较小且趋于稳定，因此，序号7 的预报精度较高。

4 结 论

为了提高飞行甲板主要设计要素确定过程的科学性，本文采用SVR 算法建立了一种飞行甲板主要设计要素的论证模型，并利用经过训练和参数优化后的回归模型对检验样本的飞行甲板各设计要素进行了预报，结果表明，多数设计要素均能获得精度较高的预报值，但少数设计要素的预报值误差较大。主要得到如下结论：

1） 尽管训练集LOO 误差与检验样本预报误差最终在数值上可能存在较大差异，但从结果上看，两者的变化趋势基本相同，因此在对SVR 模型的参数进行优化时选取前者作为目标函数是合理的。

2） 对于以舰体主尺度要素作为输入量的回归模型，经过训练集训练以及SA 优化后，其对于与飞行甲板主尺度相关的设计要素或者其他规律性较强的设计要素具有较高的预报精度，也说明这些预报结果符合当代大型航母飞行甲板主流的设计规律。

3） 斜角甲板度数以及横向位置受到较多方面因素的影响，且训练集各样本相应设计要素离散程度较大，因此这两项预报值的误差显著大于其他设计要素。

4） 计算结果反映了当代不同国家不同型号大、中型航母飞行甲板的设计风格已经趋于稳定，在飞行甲板整体布置形式没有发生较大革新的情况下，相关设计要素通常也不会有明显的变化。