山地掉层框架结构振型分解法合理振型数的研究
2020-12-16吴茜玲李英民唐洋洋
吴茜玲 李英民 ,2,* 唐洋洋
(1.重庆大学土木工程学院,重庆400045;2.重庆大学山地城镇建设与新技术教育部重点实验室,重庆400045)
0 引 言
对于线性振动体系,振型分解法是目前常用的一种动力分析方法。利用振型分解,将原N自由度体系的运动方程解耦为N个等效的单自由度体系运动方程。从原理可知,考虑所有振型能得到该方法的精确解,但在实际情况中,考虑所有振型对硬件和软件设备要求高、耗费时间多,且根据结构的受力特点,适当截断振型能得到与精确解误差在工程可接受范围内的结果,因此在对结构进行抗震分析时,适当截断振型是有必要的。
对于基础等高接地的平地结构,现有规范[1-2]规定:计算振型数应使各振型参与质量之和不小于总质量的90%。而山地掉层结构因地形环境的影响,基础修建在不同标高的场地上,与平地结构受力特征存在显著差异。已有研究表明[3-4],高阶振型对掉层结构某些部位有不可忽略的影响,若仅考虑以往精度限值下的振型数,结构会产生较大的误差。因此针对掉层结构的特殊性,如何合理截断振型是一个值得研究的问题。
为此,本文建立一山地掉层结构,通过不同控制方法对结构进行振型截断,分析结构响应的差异性,并改变结构的布置形式,探讨振型截断的影响规律,依此对山地掉层结构振型数的确定提出建议。
1 振型数的控制方法
目前常用确定振型数的方法有Edward L.W.提出的振型质量参与系数法[5]和史铁花提出的振型位移法[6]。
1.1 基本方程
假定掉层结构总层数为N,将其质量等效至各层楼板位置,各质点均有沿水平主轴方向的两个平动自由度及一个绕竖向的转动自由度,共3N个自由度。对该多自由度线性体系,在基底加速度的作用下,存在运动方程:

假定结构位移

式中:Φ为振型矩阵,且Φ=(φ1,φ2,…,φ3N)是振型向量φj(j=1,2,…,3N)的集合;q(t)为广义坐标函数向量。
1.2 振型质量参与系数法
假定方程(1)不包含阻尼力和弹性力,
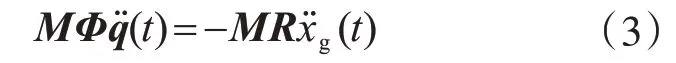

对于x方向上的单位基本加速度,j振型的质点惯性力向量为

基底剪力即为各质点惯性力之和:
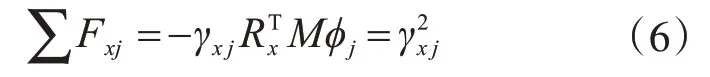
同理可得y向及绕z向转动的基底剪力,故定义振型质量参与系数为参与组合振型的基底剪力之和与结构该方向的总质量之比:

振型质量参与系数法本质是从宏观上判断地震作用,通过计算基底剪力来估量解的精确度[7]。r≥90%是一个经验数据,若满足则可忽略剩余振型的影响。
1.3 振型位移法
文献[8]表明,结构考虑所有振型时:


同理可得,j振型下y向及绕z向转动的有效特征参数都为N。则j振型下三方向的累计有效特征参数绝对值为

故本文定义t为结构在x、y向和绕z轴转动方向的累计有效特征参数的绝对值与结构总自由度3N的比值:

对应Δ= 0.1,即t需满足t≥90%。
2 不同振型数对掉层框架结构的影响
2.1 计算模型
为研究采用两种方法进行振型截断时山地掉层结构的受力差异,建立一个10 层掉层框架结构,其基本情况如图1:沿顺坡向6 跨,沿横坡向3跨,掉层部分为5 层2 跨。具体参数为:梁截面尺寸0.25 m×0.6 m,柱截面尺寸0.5 m×0.5 m,板厚0.1 m,层高3 m,柱距6 m×6 m。楼面恒载1 kN/m2,活载2 kN/m2。抗震设防烈度为7 度0.10g,地震动分组为2组,场地类型为Ⅱ类,特征周期Tg=0.4 s,水平地震影响系数最大值为0.08,各振型阻尼比均取0.05。
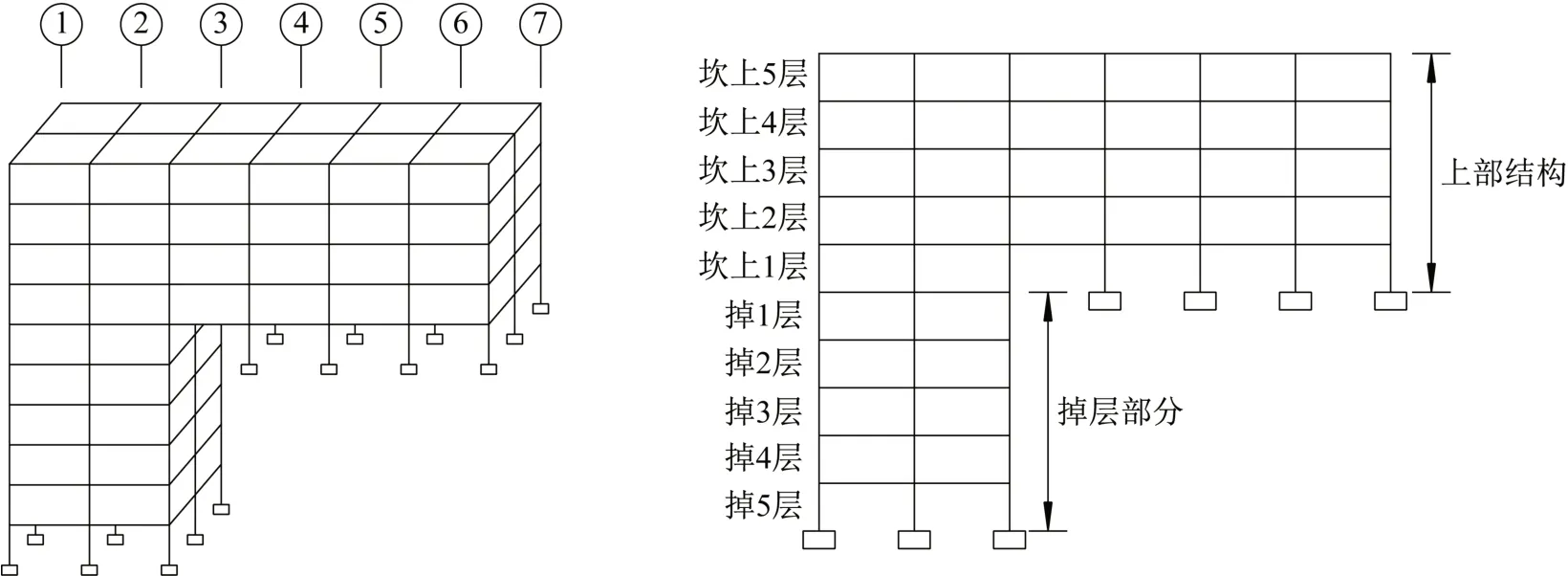
图1 结构布置图Fig.1 Structural layout
在Etabs 软件中,振型组合选择CQC 法,采用上节提到的两种控制方法进行振型截断,并分别对两种方法取不同控制精度进行结构分析。规范[1,2]有对结构累计振型质量参与系数大于90%的规定,此规定对于掉层结构部分楼层来讲,设计时可能会遗漏一些对结构反应贡献相对较大的振型,导致计算结果偏不安全,《山地建筑结构设计规程》(征求意见稿)5.1.2.1 规定:对于掉层结构,计算振型数应使各振型参与质量之和不小于总质量的95%;为与振型质量参与系数法对比,振型位移法也取相同精度,即讨论4 种情况:①r≥90%;②r≥95%;③t≥90%;④t≥95%。
在各层楼盖设置刚性隔板,结构模型即为层刚片模型,每层有沿x、y向平动和绕z轴转动3 个自由度,故认为结构总的振型数为30。经计算可知:① 满足r≥90%的最小振型数为5;②满足r≥95%的最小振型数为9;③满足t≥90%的最小振型数为6;④满足t≥95%的最小振型数为13。
2.2 结果分析
以考虑所有振型(即30 个振型)的结构响应为精确值,考虑部分振型的结构响应为计算值,将因振型截断引起的误差定义为

以式(12)得出的误差值为5%作为衡量标准[9],分析四种情况下结构的楼层剪力误差,由图2 可知:沿顺坡向,振型截断的剪力误差主要体现在掉层部分中上层和上部结构顶层,且在掉层部分更明显。控制精度为90%时,掉2 层的剪力误差超过5%;控制精度增加至95%后,各楼层剪力误差均小于5%。采用振型质量参与系数法控制时,控制精度自90%增加至95%对掉2 层影响最大,剪力误差减小了4.2%;上部结构顶层次之减小了2.9%。

图2 各楼层剪力误差Fig.2 Shear force error of each floor
坎上第4 层也有1.3%的误差减小,其他楼层并没有明显变化。采用振型位移法控制时,控制精度增加对掉2 层的剪力误差影响更大,减小了5.8%,其他楼层与采用振型参与系数法控制无明显差别。将两种控制方法对比:在相同精度90%时,二者的剪力误差无明显区别;在95%时,振型位移法在结构掉2 层的剪力误差比振型质量参与系数法少1.5%,效果更好。
沿横坡向,剪力误差的规律与顺坡向相似,振型截断的剪力误差主要体现在掉层部分中上层和上部结构顶层,但在上部结构顶层更明显。控制精度为90%时,上部结构顶层剪力误差超过5%;控制精度增加至95%后,各楼层剪力误差均小于5%。采用振型质量参与系数法控制时,控制精度增加对上部结构顶层的影响最大,剪力误差减小了3.6%;而掉层部分在掉1层体现更明显,误差减小了2.1%。采用振型位移法控制时,精度依旧对上部结构顶层影响最大,精度增加时剪力误差减小了5%;对掉层部分中上层的影响较均匀,精度增加时结构掉1~3 层的剪力误差都减小了1%左右。将两种控制方法对比:在相同精度90%时,振型位移法在掉层部分的剪力误差更小,主要体现在掉 1 层,其次是掉 4 层、5 层;而在 95% 时,振型位移法在结构掉层部分和上部结构顶层的剪力误差都明显小于振型质量参与系数法,控制效果更好。
总的来说,振型截断的剪力误差主要体现在掉层部分中上层和上部结构顶层,沿顺坡向对掉层部分影响更大,沿横坡向对上部结构顶层影响更大;控制精度增加至95%后,各楼层剪力误差均小于5%;振型位移法的控制效果比振型质量参与系数法好,并且在横坡向的体现更加明显。
在横坡向,山地结构竖向不规则的特点使其存在先天的扭转效应[10-11],在该方向地震作用下,结构各榀框架剪力分布不均匀且存在较大差异,楼层剪力并不能完全衡量内力计算结果的精确度。故沿横坡向,将结构看作并联式模型,对结构各榀框架的剪力进行误差分析,结果如图3 所示,图中框架编号按图1 所示。因结构掉2~5 层的剪力误差分布规律与掉1 层相似,本文不一一画出。
在掉层部分及坎上1 层的非接地侧,采用振型质量参与系数控制时,控制精度的增加对掉层部分靠近接地侧的框架剪力影响较大;采用振型位移法时,控制精度的增加对此部分的剪力误差影响有限。
在坎上1 层的接地侧及坎上2~5 层,相同精度下两种控制方法的剪力误差趋势类似,控制精度的增加对接地侧的框架剪力影响较大,且精度增大时各楼层误差都有明显减小。但各楼层误差最大的框架是不同的:在坎上1 层,远离非接地侧的边两榀框架的剪力误差最大;在坎上2 层则是一个先增大后减小的趋势,剪力误差在中部框架最大;而在坎上3~5层,剪力误差从靠近非接地侧起逐渐增大,且楼层越高误差越大。
四种情况下结构层间位移角误差由图4 可知:与剪力误差基本相似,层间位移角误差也主要体现在掉层部分及上部结构顶层,但各楼层误差均未超过5%,受振型截断的影响比剪力小。
3 结构布置对误差的影响
为进一步研究振型数对山地结构受力的影响,以上节模型为标准,对比不同结构布置如掉层层数、掉层跨数、坎上楼层数时振型截断对误差的影响。共设计9 个不同模型,模型的命名原则为DXKY-Z(掉X层Y跨-坎上 Z 层)。以r≥90% 和95%、t≥90%和95%进行振型截断,模型信息及振型截断结果如表1所示。

图3 不同楼层各榀框架的剪力误差Fig.3 Shear force error of each frame on different floor
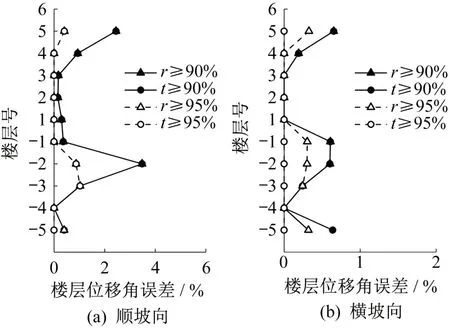
图4 层间位移角误差Fig.4 Interlayer displacement angle error
改变掉层跨数和坎上楼层数,两种控制方法在控制精度从90%增加至95%时,振型数均有显著增大;改变掉层层数,以振型质量参与系数法控制时,控制精度的增加对振型数影响略大;以振型位移法控制时,若掉层数较少,控制精度的增加对振型数的影响并不明显。
应注意到,对于模型D4K2-5,取7阶振型时t=96.1%,取8、9 阶振型时t=95.7%、t=95.4%,可见t并非随振型数增加而单调增大。因为振型位移法是和的概念,可能会出现大值项补小值项的情况,即存在t是“震荡”的情形。
经计算,层间位移角的误差规律与剪力基本相似,故为简化篇幅,本文只列出结构布置对剪力误差的影响。
3.1 结构布置对顺坡向剪力误差的影响
沿顺坡向,不同结构布置、不同控制方法下各楼层剪力误差如图5 所示,由图可知:控制精度为90%时,模型在掉层部分误差会超过5%,控制精度增加至95%,各模型各楼层的剪力误差均小于了5%。

表1 不同控制方法所需振型数Table 1 Number of modes required for different control methods
(1)对不同掉层层数模型,控制精度以振型质量参与系数法控制时:在掉层部分,模型掉层数较少时,控制精度增加对掉层底部的剪力影响很大,模型D3K2-5 在掉2 层的误差减少量达到了9%,而模型D2K2-5 达到了20%;模型掉层数越多,精度增加相较于对掉层底部,对掉层部分中上层的剪力影响更大,D4K2-5、D5K2-5 在掉 2 层的误差减少量最大。以振型位移法控制时,控制精度的增加对掉层部分中上层影响较大,并且在掉层数多时体现更明显。
(2)对不同掉层跨数模型,两种控制方法的变化规律大致相似,精度增加对掉2 层的剪力影响最大,且精度增加的影响随掉层跨数的增加而减小。振型位移法对掉2 层的控制效果要略优于振型质量参与系数法,模型D5K2-5在前者的控制下误差减小5.8%,后者减小4.2%;D5K3-5 前者减小4.2%,后者减小1.6%;两种控制方法下精度增加对模型D5K4-5都无明显影响。
(3)对坎上不同层数模型,两种控制方法的变化规律大致相似,精度增加对掉2 层的剪力影响最大,而误差也随着坎上层数的增加呈现先增大后减小的趋势,模型D4K2-5 的误差减小13.7%,D3K2-5及D5K2-5的误差都只减小4%左右。

图5 沿顺坡向各楼层剪力误差Fig.5 Shear force error of each floor along the slope
3.2 结构布置对横坡向剪力误差的影响
沿横坡向,不同结构布置、不同控制方法下各楼层剪力误差如图6 所示,由图可知:控制精度为90%时,模型在上部结构顶层的误差会超过5%,控制精度增加至95%,各模型各楼层的剪力误差均小于5%。
(1)对不同掉层层数模型,以振型质量参与系数法控制时,精度增加对上部结构顶层的剪力误差影响最大,各模型误差均减小3%左右;对于掉层部分,掉层数少时,精度增加对掉层底部的剪力影响更大,随着掉层数的增加,对掉层部分中上层影响更大。振型位移法的控制效果较差,精度增加对模型D5K2-5 影响较大,对模型D2K2-5、D3K2-5、D4K2-5影响不明显。
(2)对不同掉层跨数模型,上部结构顶层是受精度影响最大的楼层;在掉层部分,以振型质量参与系数法控制时,精度增加对掉层跨数少的模型影响更大,模型D5K2-5各掉层的剪力误差都有不同程度的减小,而模型D5K3-5 及D5K4-5 仅体现在掉1 层。以振型位移法控制时,精度增加主要影响掉1、2层的剪力,并且跨数少时影响大。
(3)对坎上不同层数模型,上部结构顶层是受精度影响最大的楼层,且坎上层数越多,精度影响越大。在掉层部分,以振型质量参与系数法控制时,精度增加对掉1 层的影响最明显,模型D5K2-3 的变化最大,减小2.1%;以振型位移法控制时,精度增加对模型D5K2-3 掉1 层影响最大,误差减小2.1%,而模型D5K2-4掉2层的误差变化最大,减小1.1%,可见随着坎上层数的增加,受精度影响最大的楼层由掉1层变化至掉2层。

图6 沿横坡向各楼层剪力误差Fig.6 Shear force error of each floor along the cross slope
4 结 论
(1)振型分解法对山地掉层框架结构是适用的,振型质量参与系数法是通过计算基底剪力来估量解的精确度;振型位移法是和的概念,在计算过程中可能会出现大值项补小值项的情形。振型数的截断可能会忽略对局部楼层有显著影响的振型,对结构安全造成影响。对山地掉层框架结构而言,95%的控制精度能将各楼层剪力误差控制在5%范围内。
(2)振型截断的剪力误差主要体现在掉层部分的中上层和上部结构顶层,沿顺坡向对掉层部分影响更大,沿横坡向对上部结构顶层影响更大;在横坡向,由于结构的扭转效应,结构各榀框架剪力误差存在较大差异,掉层部分剪力误差较大的框架为靠近接地侧的框架,坎上1 层为靠近接地侧的非接地框架,上部结构则为接地侧框架。
(3)沿顺坡向,对于不同掉层层数模型,掉层数越少,随精度增加两种控制方法的差异越明显;对于不同掉层跨数模型及坎上层数模型,两种控制方法的规律相似,精度增加对掉层部分中上层的剪力影响最大,且精度的影响随掉层跨数的增加而减小,随坎上层增加数呈先增大后减小的趋势。沿横坡向,上部结构顶层是受精度影响最大的楼层,且两种控制方法有差异,在掉层层数不同时体现最明显。掉层跨数、坎上层数越少,精度增加的影响越大。
