上承式异型拱桥的设计

2020-12-16王银刚李玉美

结构工程师 2020年5期

王银刚李玉美

（1.湖北第二师范学院BIM技术应用工程中心，武汉430205；2.湖北省BIM智慧建造国际科技合作基地，武汉430205；3.中铁第四勘察设计院集团有限公司，武汉，430063）

0 引言

拱桥是一种历史悠久的桥型，以跨越能力大、承载力高、建造材料丰富、造价经济、造型美观等特有的优势而成为建筑历史悠久、不断发展的桥梁形式。随着科技的发展，人们桥梁已不单纯作为交通线上重要的工程实体，而且亦作为一种空间艺术结构物存在，异型拱应运而生。

异型拱尚无明确定义，通常泛指非对称拱。现有的异型拱桥多为下承式系杆拱（图1（a）），据可查的文献，上海市政工程研究院的李生智等［1-2］在1992 年首次提出了异型拱桥这一种新型系杆拱桥结构体系，文献［3-5］对该类系杆拱桥进行了力学分析，国外也有文献［6］对网状系杆异型拱桥的设计进行了研究。而对于上承式异型拱桥的研究则较少，中铁四院［7］曾对上承式异型拱桥（图1（b））的拱轴线的选型做了研究，提出了在均变荷载作用下，三种常规的拱轴线（圆曲线、抛物线和悬链线）中，当异型拱大拱侧（即拱顶距离拱脚较远侧）采用悬链线、小拱侧（即拱顶距离拱脚较近侧）采用抛物线时主拱圈的弯矩最小，并引入了异型系数描述异型拱的不规则程度，研究了主拱圈的受力随失跨比、异型系数等的变化趋势。

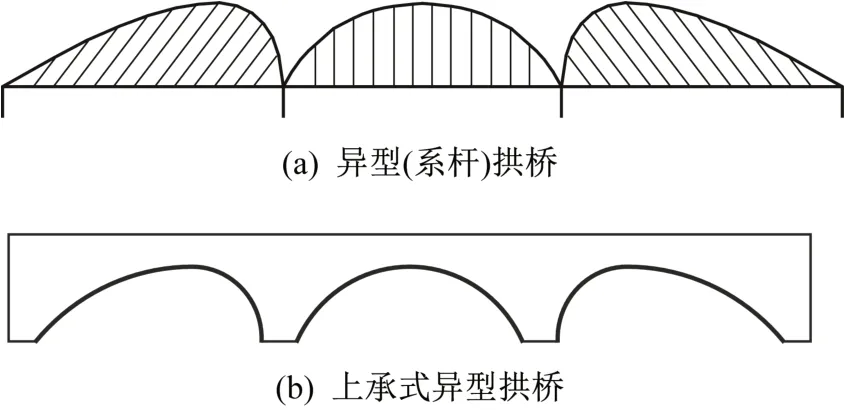
图1 两种异型拱桥造型比较Fig.1 Appearance comparison of two different special-shape arch bridges

异型拱是一种非对称结构，受荷模式为从拱顶至拱脚均匀变化的荷载，在保证桥梁美学特征的前提下，不存在一条理想的恒载压力线使主拱圈内的弯矩为零，因此对主拱圈的受力进行优化是提高异型拱桥经济性和安全性的关键。本文首先研究了上承式异型拱桥主拱圈受力优化的途径，然后以某上承式异型拱桥的设计实例介绍了异型拱桥的总体设计思路，力求为该类桥梁的设计提供参考。

1 异型拱主拱圈受力优化

1.1 优化拱轴线线型

三种常规的拱轴线中，当异型拱大拱侧采用悬链线，小拱侧采用抛物线时，主拱圈的弯矩最小［7］。在同一坐标系下考察异型拱桥各拱轴线的相对位置，如图2所示，悬链线竖向坐标最靠上，抛物线竖向坐标最靠下，由于异型拱的非对称性，为了使拱截面弯矩最小，须使大拱侧和小拱侧所受的不平衡荷载差值最小，即大拱拱上荷载取小值，小拱拱上荷载取大值。由此推测：在同一荷载边界下，异型拱大拱拱轴线坐标越靠上、小拱拱轴线坐标越靠下的拱轴线组合为最优拱轴线，下面用算例来验证此推测。

图2 拱轴线相对位置Fig.2 Relative position of arch axis

【算例1】异型拱矢跨比f=1/5，跨径L=25 m，拱顶偏移桥跨中心线δ=2.95 m。主拱圈计算宽度为1 m，拱圈厚度为0.5 m，混凝土标号为C40，不计主拱圈的自重，拱脚采用固结。通过调整大拱侧悬链线拱轴系数m和小拱侧抛物线次数n来改变拱轴线的方程，m分别取 4.33、6.5 和 8.1，n分别取2、1.9和1.8。由此得到的拱轴线在同一坐标系下的相对位置关系及计算图示见图3。

图3 算例1计算图示（单位：m）Fig.3 Calculate diagram of example 1（Unit：m）

在不同m和n下对大拱和小拱的拱轴线两两组合，可得到9组不同拱轴线组合下主拱圈的最大弯矩值，如表1 所示。结果表明，当保持大拱侧拱轴线不变，小拱侧拱轴线曲线次数越低（即小拱拱轴线竖向坐标越靠下），拱内的弯矩值越小；同样，当保持小拱侧拱轴线不变，大拱侧拱轴线的竖向坐标越靠上，拱内弯矩越小，结论与前述推测相符。

表1 不同拱轴线组合下拱圈最大弯矩值Table 1 The maximum bending moment of arch ring in different combinations of arch axes kN·m

进一步分析可知，若将异型拱大拱和小拱拱轴线坐标同时调整，可以使拱内弯矩向目标弯矩的优化速度加快。以本算例中的3 组拱轴线为例：

组合1：悬链线（m=4.33）+抛物线（n=2）；

组合2：悬链线（m=6.5）+抛物线（n=1.9）；

组合3：悬链线（m=8.1）+抛物线（n=1.8）。

拱轴线组合1调整到组合3的过程中，拱内最大弯矩按表1 中对角线方向递减，弯矩值降幅明显，主拱圈最大弯矩值由组合1 的485.3 kN·m 减小为组合3的265.6 kN·m，减小了45.3%。以大拱拱脚为x坐标原点，可得出此优化过程中，各拱轴线组合下拱内弯矩的变化曲线（图4），可见，拱脚、拱腰和拱顶的弯矩均有不同程度减小。

图4 算例1弯矩曲线Fig.4 Bending moment curve of example 1

需要注意的是，建造异型拱往往是由于景观需要，异型拱的受力优化应以保持外形美观为前提，不能一味追求主拱圈的受力而忽视桥梁美观。

1.2 未知荷载系数法优化异型拱弯矩

如前所述，异型拱内的弯矩主要是由拱顶两侧不对称荷载引起，因而通过调整拱顶两侧的荷载分布也成为优化异型拱受力的思路之一。未知荷载系数法具有通过控制约束条件使计算结果满足约束条件及目标函数各变量值的功能，将异型拱拱圈的目标弯矩值作为约束条件，以拱背填土荷载作为未知荷载，可求得满足约束条件的填土荷载系数，从而达到优化异型拱弯矩的目的。

【算例2】计算条件同【算例1】，拱轴线采用组合1，拱顶两侧采用不同的拱背填料，在考虑拱自重的情况下，使拱内的恒载最大弯矩绝对值不大于100 kN·m。

图5 算例2计算模式Fig.5 Calculate diagram of example 2

将异型拱大拱拱背的填土容重设为1 kN/m3，通过MIDAS/Civil 有限元软件进行计算，可求得填土容重对拱圈弯矩的影响矩阵。然后，将大拱侧的填土荷载容重设为未知荷载x，设定的目标条件为所有节点的弯矩范围为-100～100 kN·m，可求出满足目标条件的多组解，从中选择一组实际可行的解即可。经计算，本例解得x=10.4（对应大拱侧填土容重为1×10.4 kN/m3）时可使主拱圈内的最大弯矩不超过100 kN·m，主拱圈弯矩图见图6，此时拱背填料可考虑采用工程废弃土和泡沫塑料块的混合填料（容重为7～13 kN/m3）。

图6 算例2弯矩图（单位：kN·m）Fig.6 Moment diagram of example 2（Unit：kN·m）

本例的荷载条件较为简单，实际应用时，可以有多个未知荷载，可以是集中荷载、均布荷载和均变荷载，有时设置的限制条件过于苛刻，以至于没有满足该条件的解，这时可以放宽限制条件或改变荷载的分布。另一方面，通过本例也可以看出，相比于优化拱轴线，用未知荷载系数法反求拱顶荷载更为直接和有效。

2 工程实例

2.1 工程概况

某景观桥跨越山区小型湖泊，无通航要求。该桥采用上承式实腹三连拱桥，中拱采用对称拱，两边拱采用异型拱，整个桥梁结构又形成以中拱中心线对称的对称结构。桥梁在延续了古典“拱”造型的同时，又使拱轴线的形式多样化，造型新颖、奇特，成为青山碧水之间的一抹亮色。

2.2 桥梁总体设计

2.2.1 桥孔布置

1）跨径组合

图7 上承式异型拱成桥效果图Fig.7 Deck special-shape arch bridge effect picture

连续拱桥设计时，宜选择桥墩处水平推力合力较小的孔跨方案，在同等跨径、同等矢跨比下，异型拱的水平推力与规则拱相当［7］，因此宜采用等跨连拱体系，本桥采用（3×24）m 上承式异型拱桥。

2）矢跨比

本桥桥高约11 m，由于异型拱主拱圈承受了较大的弯矩，有效降低拱圈弯矩的方法就是减少拱桥恒载的重量，因此拱顶距桥面的距离不宜过大。同时，拱桥矢跨比越大，拱脚推力越小，对两岸桥台越有利，因此宜选择稍大的矢跨比。综合上面以上两点，结合桥位处的湖水常水位，本桥取矢跨比为6.5 m，拱顶距离桥面1 m。

3）异型拱的形式与异型系数

本桥为景观桥，桥梁的美观应是首要考虑的因素，为增加异型拱的动态感，在小拱拱脚处采用“回头”曲线（图8），但“回头”曲线使异型拱的受力明显不合理，因此用外部装饰的方法在小拱拱脚处加装饰拱来避免拱桥的不利受力状态。

图8 异型拱拱桥处理Fig.8 Special-shape arch foot processing chart

异型系数［7］定义为大拱与小拱在拱脚连线上水平投影长度之比，如图2所示，异型系数ξ为

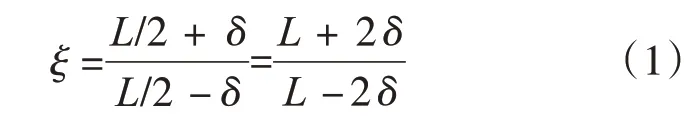
式中：L为异型拱跨径；δ为异型拱拱顶偏移拱桥中心线的水平距离。

异型系数的选取关系到异型拱的受力，同时也是影响桥梁美观的重要指标。异型系数越大，异型拱的不规则程度就越高，拱内的弯矩也越大，受力往往越不利，但是较大的异型系数美观效果较好。本桥选取的边拱异型系数为2.286，此时拱的重心处于拱左、右两侧的“黄金分割点”附近，符合人们的审美。

2.2.2 拱上建筑的选择

拱上建筑有实腹式和空腹式两种，实腹式拱上建筑构造简单、施工方便，但填料数量较多，恒载较重，所以一般用于小跨径的拱桥；空腹式拱上建筑恒载较轻，常用于大、中跨径的拱桥。

为减小异型拱在恒载作用下的弯矩，本桥在主拱圈上设置四道纵墙，在墙上现浇实心桥面板，形成“中空”的结构。桥梁横断面如图9所示。

图9 桥梁横断面布置图（单位：cm）Fig.9 Cross section of the bridge（Unit：cm）

2.2.3 拱轴线的选择及优化

桥梁中拱为规则拱，拱轴线采用悬链线是最贴近恒载压力线的线型，因此中拱拱轴线采用悬链线，无优化余地。两边拱采用异型拱，根据文献［7］的研究成果，异型拱采用“悬链线（大拱）+抛物线（小拱）”的拱轴线组合时，主拱圈内的弯矩最小，但异型拱的异型系数较大时，小拱采用抛物线的拱轴线从视觉上看在拱顶处的过渡有突兀感，即使在小拱侧做装饰拱，也无法达到比较好的美观效果，表2为两种拱轴线下的详细比较。

综合表2的比较，“悬链线+圆弧线”拱内最大弯矩仅比“悬链线+抛物线”拱稍大，但美观效果要比后者好，本桥推荐“悬链线+圆弧线”的拱轴线组合。小拱侧的“回头”曲线是本桥美观的焦点所在，小拱侧采用的圆弧线已无优化余地，但可以通过调整大拱侧悬链线的拱轴系数来降低大拱侧的拱内弯矩，使其在结构配筋相同的情况下能有较大的承载能力富余。大拱侧拱轴线的优化方向为增高其竖向坐标，反映到拱轴线方程中即增大拱轴系数，优化拱轴线的同时还需兼顾桥梁美观。

表2 异型拱技术、经济及美学比较Table 2 Technical，economic and aesthetic comparisons of special-shape arches

拱脚恒载集度gj=534.4 kN/m，拱顶处荷载集度gd=196.4 kN/m，拱轴系数m=gj/gd=2.72。本桥初步设计时，通过试算，在兼具美观的前提下将大拱拱轴系数增大到4.67，恒载作用下的计算结果见表3，大拱拱脚弯矩减小了19.7%，拱脚推力变化程度较小。因此本桥异型拱采用“悬链线+圆弧线”的拱轴线组合，悬链线拱轴系数取4.67。

2.2.4 下部结构

据桥位区地形地貌、岩土分布特征、各岩土层的工程地质特性，结合拟建桥梁的荷载分布特点，桥梁墩、台最适宜的基础形式为桩基础。桩基础类型采用嵌岩桩，以中风化花岗岩作桩端持力层。